Конспект урока по Геометрии "Площадь параллелограмма"
М-8 у-59


 Разработка урока по теме «Площадь параллелограмма».
Разработка урока по теме «Площадь параллелограмма».
Автор: Миронова Светлана Сергеевна
Площадь параллелограмма.
«Считай несчастным тот день или тот час,
в который ты не усвоил ничего нового
и ничего не прибавил к образованию».
Ян Амос Каменский
Цель урока: изучить теорему о площади параллелограмма.
Задачи урока:
образовательные – формирование практических навыков вычисления площадей многоугольников в ходе решения задач (квадрат, прямоугольник, параллелограмм);
развивающие – активизация мыслительной деятельности: перенос знаний в новую ситуацию;
воспитательные – развитие познавательного интереса, культуры математической речи, способности критически, объективно оценивать действия товарищей и свои.
Оборудование: компьютер, проектор, бумажные модели параллелограмма, презентация.
Ход урока.
Организационный момент.
Какую тему мы начали изучать два урока назад?
Сегодня на уроке мы научимся вычислять площадь еще одной фигуры – параллелограмма.
В тетрадях число, классная работа, тема урока.
Актуализация знаний учащихся.
Площади каких фигур вычислять мы умеем?
Как найти площадь квадрата?
Как вычислить площадь прямоугольника?
Проверим некоторые задачи из домашней работы.
Приготовить рисунки на доске. Выходит уч-ся и устно объясняет решение.
№ 454.
а) S=ab=250
x x*2,5x=250
2,5x
x=10
стороны 10см и 25 см.
№ 456.
Изучение нового материала.
Начертите в тетради квадрат, прямоугольник и параллелограмм.
Подпишите под ними формулы для нахождения площади этих фигур.
Что нужно знать для нахождения площади квадрата? Что такое а в квадрате? Какие эти стороны? (перпендикулярные)
Что нужно знать для нахождения площади прямоугольника?
Какие это стороны?
Как вы думаете, как мы будем искать площадь параллелограмма?
Эти стороны перпендикулярны?
А как получить перпендикулярный отрезок, который можно использовать для нахождения площади параллелограмма?
Это отрезок называется высотой параллелограмма.
С помощью чего удобно проводить перпендикуляр?
Сколько высот можно провести из одной вершины?
Итак, вынесем предположение о том, как мы будем находить площадь параллелограмма.
И сейчас мы докажем, что вы оказались правы.
Доказательство теоремы по слайду презентации.
Найдем подтверждение нашей правоты в учебнике. По оглавлению находим главу 6 параграф 2 пункт «Площадь параллелограмма». Прочитаем теорему.
Закрепление изученного.
Задачи со слайдов. Решение первых трех задач устное, следующих трех - письменное.
Работа в рабочих тетрадях.

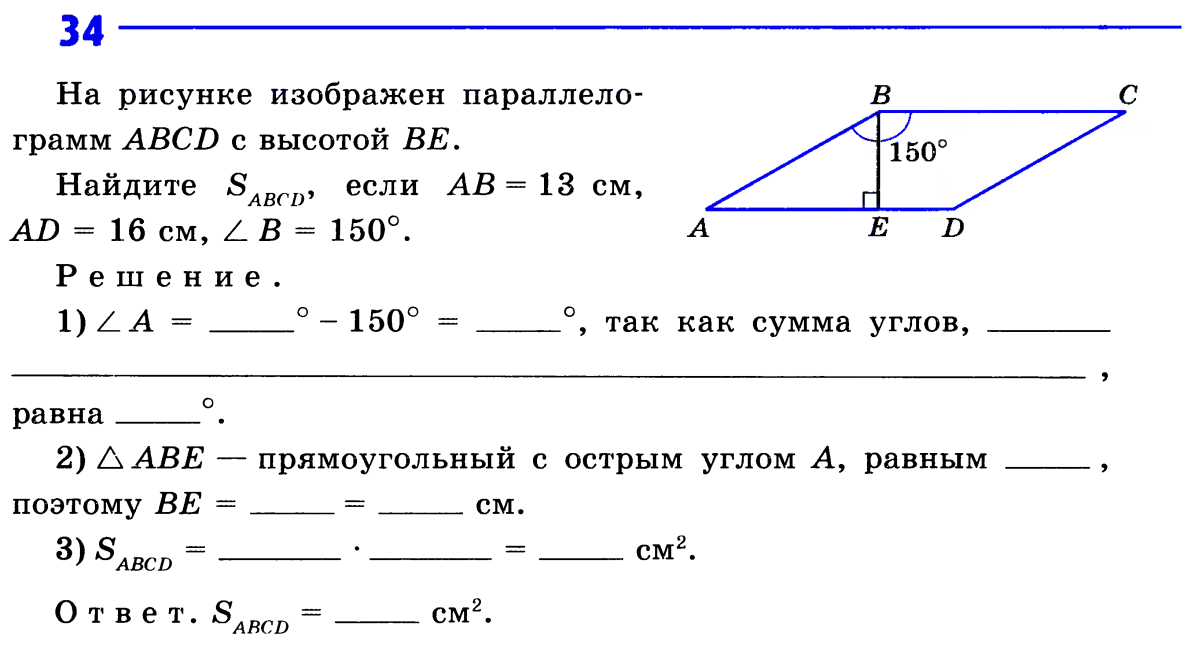
№ 463 из учебника.
Подведение итогов урока.
Вернемся к словам Яна Амоса Каменского. Как вы оцените этот урок: как счастливый час или несчастный?
Сумели ли вы усвоить новое?
Что удалось вам прибавить к образованию?
Домашнее задание.
П. 51 – теорема + доказательство; №№ 459ав, 460, 464а.
Литература.
Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. Геометрия, 7-9.
Л.С. Атанасян, В.Ф. Бутузов, Ю.А. Глазков, И.И. Юдина. Рабочая тетрадь по геометрии для 8 класса.





Нравится материал? Поддержи автора!
Ещё документы из категории геометрия:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ