Конспект урока по Геометрии "Соотношения между сторонами и углами прямоугольного треугольника"
Оноприенко Л.Н.;
учитель математики ШЛ №27
(из опыта работы).
Урок по теме: Соотношения между сторонами и углами прямоугольного треугольника.
Тип урока: Урок решение задач.
Цель урока: Применение знаний, умений и навыков по теме "Соотношения между сторонами и углами прямоугольного треугольника" к решению задач прикладного характера.
Задачи урока:
1) Повторить базовые знания по теме.
Показать их применение к решению прикладных и практических задач.
2) Воспитать: ответственность, активность, инициативу и творческий
подход к делу, дух соревновательности.
3) Развивать: Практические умения и навыки, элементы моделирования
и конструирования, поисково-исследовательскую деятельность,
логическое мышление, вычислительные навыки, геометрическое видение.
Метод: Практический с элементами моделирования и конструирования, частично-поисковой деятельностью.
Средства:
Интерактивная доска.
Тест по теме " Теорема Пифагора" (логические цепочки в задачах на готовых чертежах).
Инструкция по выполнению теста.
Таблицы с задачами на готовых чертежах.
5) Карточки с задачами прикладного и практического характера.
6) Классмейты, таблицы Брадиса.
7) Презентация исторического материала " О значении теоремы Пифагора."
8) Набор инструментов для построения прямого угла.
9) Оценочный лист.
План урока.
1.Организационный момент. Постановка цели урока.
2.Проверка базовых знаний и умений по теме: "Решение прямоугольных треугольников"
а) Ребусы ( на повторение основных понятий )
б) Работа по готовым чертежам.
в) Практическая работа по построению прямого угла.
3. Тест по теме " Теорема Пифагора" ( логические цепочки в задачах на готовых
чертежах.)
4.Решение прикладных и практических задач.
5. Исторический экскурс (о значении теоремы Пифагора )
6. Подведение итогов урока.
Выставление оценок.
Рефлексия.
7. Постановка домашнего задания.
Перед уроком на интерактивной доске демонстрируется слаид-шоу фрагментов красивейших архитектурных сооружений столицы.
Начинается урок. Учитель просит ребят прокомментировать увиденный сюжет и дать ему название. Затем говорит о том, что уже очень многое изучено по треугольнику в том числе по прямоугольному и объявляет конкурс на лучшую презентацию мини-проекта "Астана в геометрических образах".
Главный сюжет - пространственный аналог треугольника: треугольная пирамида в архитектурных сооружениях города Астаны. Срок-1месяц.
Х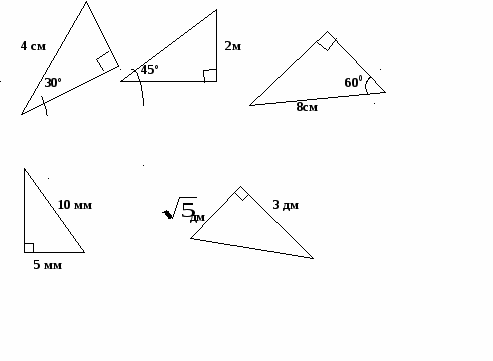 од урока.
од урока.
№
п/п
Содержание учебного материала.
Деятельность учителя и ученика.
1.
Организационный момент. Постановка цели урока.
Тема: Соотношения между сторонами и углами прямоугольного треугольника.
Цель урока: Применение знаний, умений и навыков по теме "Соотношения между сторонами и углами прямоугольного треугольника" к решению задач прикладного и практического характера.
Проверяет готовность класса к уроку, объявляет цель урока.
2.
Проверка базовых знаний и умений по теме: "Решение прямоугольных треугольников"
а) Разгадать ребусы (на повторение основных понятий).
( Приложение 1).
Землемеры древнего Египта для построения прямого угла использовали бечевку, разделенную узлами на двенадцать равных частей. Покажите. как они это делали.
Указание: в углах должны быть узлы.
На интерактивной доске. Фронтальная работа. Параллельно с фронтальной работой группа учащихся из трёх человек выполняет практическую работу по построению прямого угла; затем перед классом демонстрируют результат, делают обоснование, используя обратную теорему Пифагора.
б) работа по готовым чертежам:
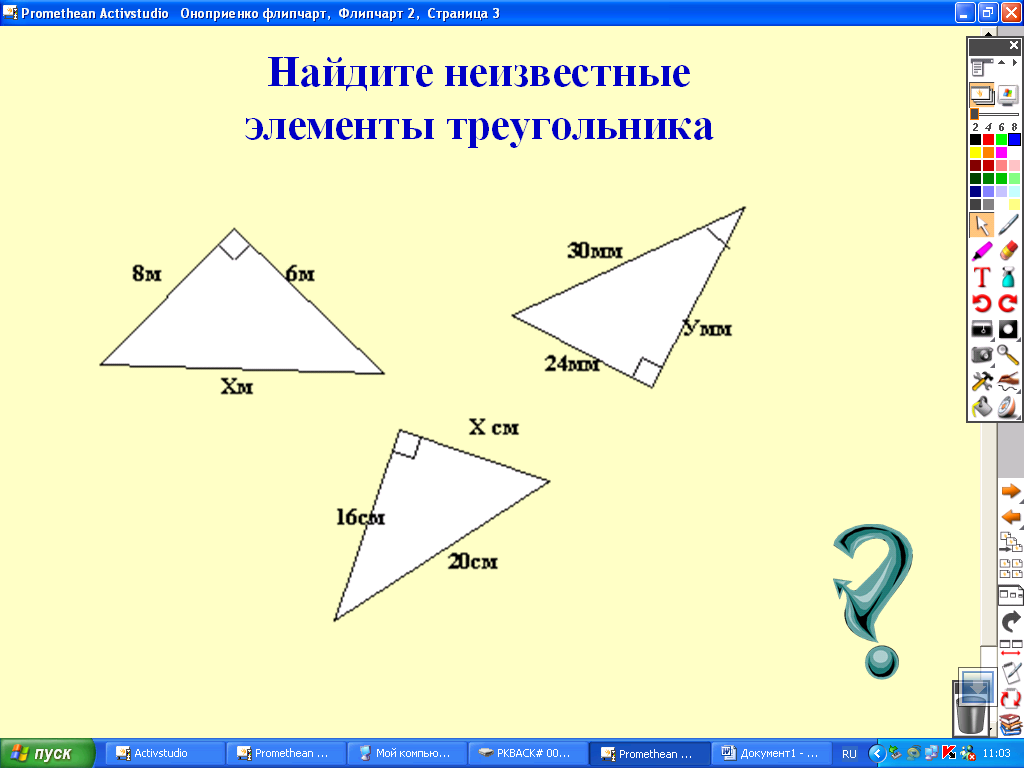
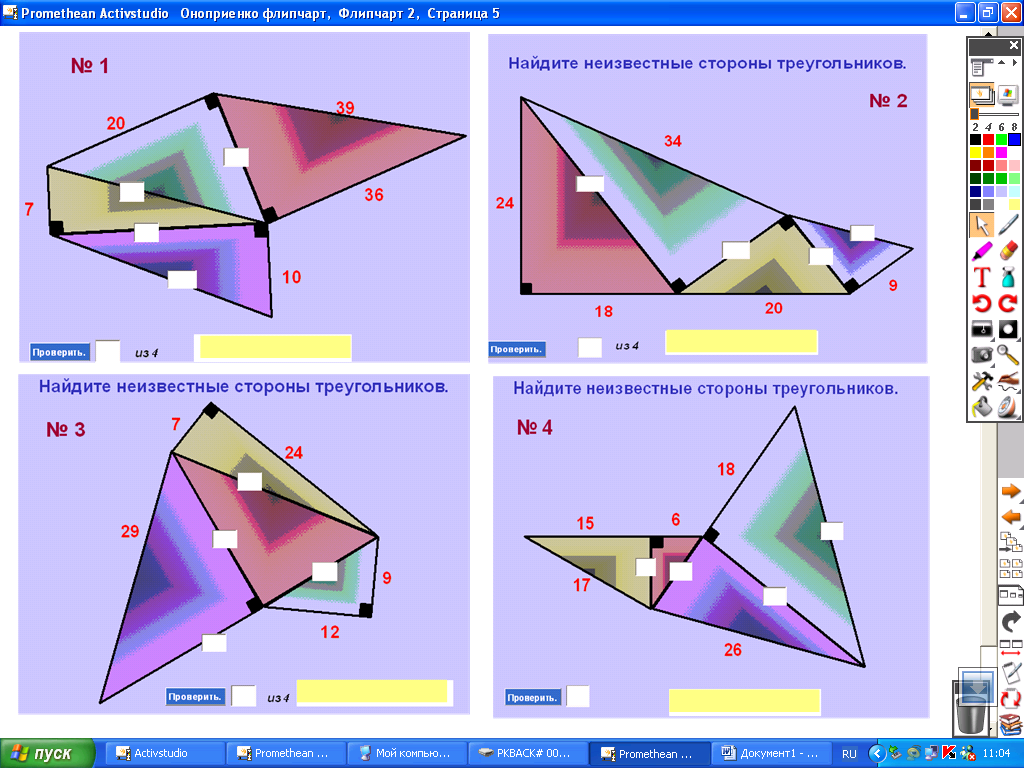
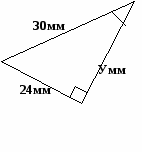 1)найдите неизвестные элементы треугольника
1)найдите неизвестные элементы треугольника
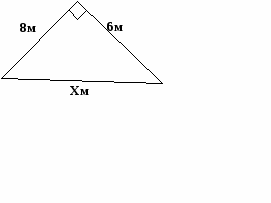
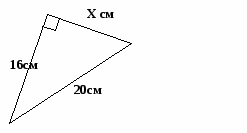
( Взаимно обратные задачи; используются пифагоровы тройки).
На интерактивной доске.
Устная фронтальная работа оценивается жетонами.
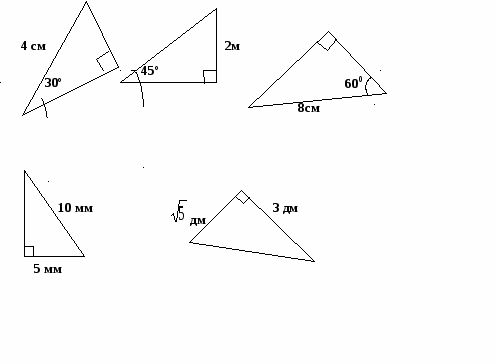
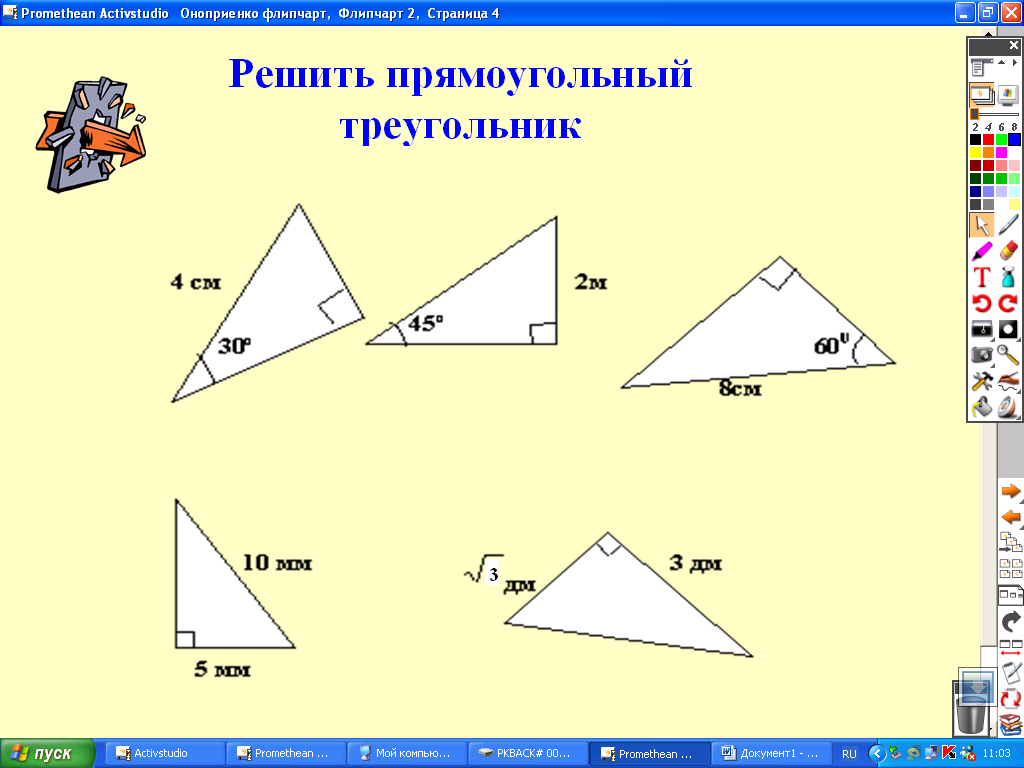
2) Решить прямоугольный треугольник
Подводится итог работы по проверки базовых знаний
Учитель перед началом работы задает вопросы:
Что значит решить прямоугольный треугольник?
Что позволяет решить прямоугольный треугольник?
а) теорема Пифагора
б) значения sin, cos, tg,ctg острых углов прямоугольного треугольника
в) теорема о сумме углов треугольника
3. Определяется ли однозначно треугольник по углам
По оценочному листу
3
Инструкция по выполнению теста:
вычислите неизвестные стороны прямоугольных треугольников на чертежах;
запишите найденные значения в пустые прямоугольники, размещенные на неизвестных сторонах;
сделайте проверку после каждого теста;
результат покажите учителю, или запишите в тетрадь;
Задание 1-4 см. приложения 2
Самооценка по критериям указаным в оценочном листе ( приложение 3)
Логические цепочки в задачах на готовых чертежах (тесты по теме: «Теорема Пифагора»).
Каждой паре учащихся на стол выкладывается инструкция по выполнению теста. (работа в парах)
Каждой паре учащихся дается таблица с комбинацией прямоугольных треугольников и инструкция по выполнению задания. Проверка идет на интерактивной доске, учащиеся вписывают верные ответы в пустые квадратики, параллельно с доской идет самоконтроль и самооценка. Ответ записывается на карточку каждым учеником в виде четверки чисел. Записывается количество верных ответов.
4
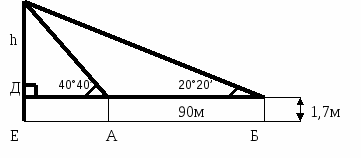
Решение прикладных и практических задач.
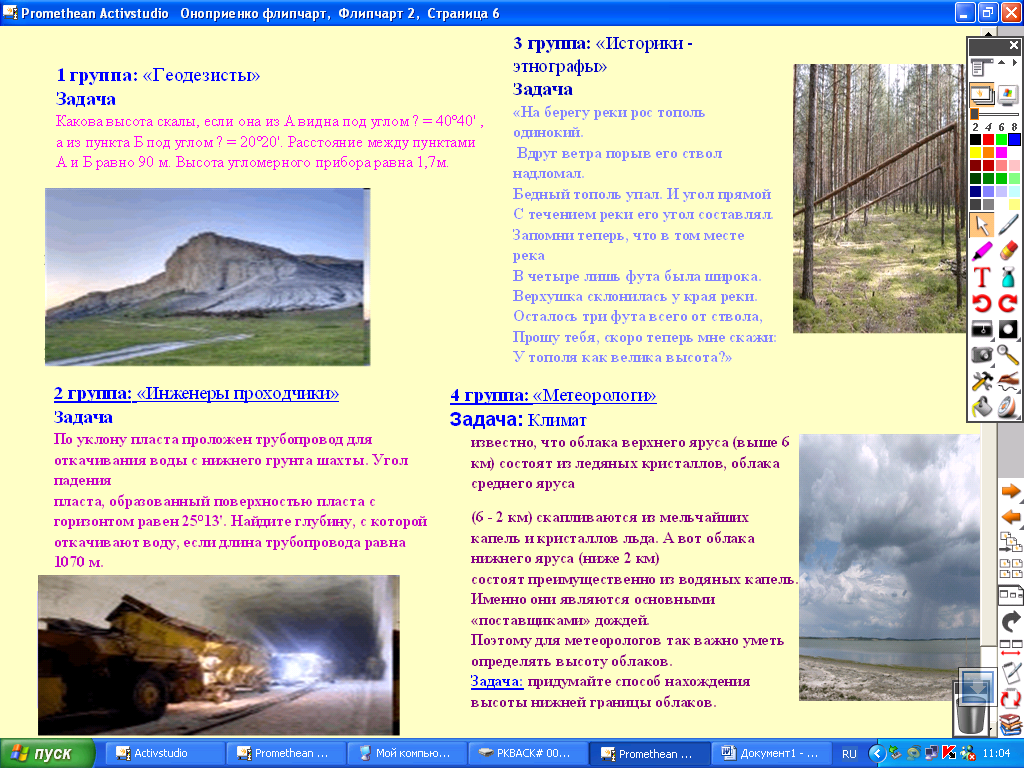
1 группа: «Геодезисты»
Задача
Какова высота скалы, если она из А видна под углом α = 40°40’, а из пункта Б под углом β = 20°20’. Расстояние между пунктами А и Б равно 90 м. Высота угломерного прибора равна 1,7м.
Ответ: 60,3 м
2 группа: «Инженеры проходчики»
Задача
По уклону пласта проложен трубопровод для откачивания воды с нижнего грунта шахты. Угол падения пласта, образованный поверхностью пласта с горизонтом равен 25°13’. Найдите глубину, с которой откачивают воду, если длина трубопровода равна 1070 м.
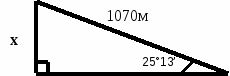
3 группа: «Историки - этнографы»
Задача
«На берегу реки рос тополь одинокий.
В друг ветра порыв его ствол надломал.
друг ветра порыв его ствол надломал.
Бедный тополь упал. И угол прямой
С течением реки его угол составлял.
Запомни теперь, что в том месте река
В четыре лишь фута была широка.
Верхушка склонилась у края реки.
Осталось три фута всего от ствола,
Прошу тебя, скоро теперь мне скажи:
У тополя как велика высота?»
4 группа: «Метеорологи»
Задача: Климат
известно, что облака верхнего яруса (выше 6 км) состоят из ледяных кристаллов, облака среднего яруса ( 6 – 2 км) скапливаются из мельчайших капель и кристаллов льда. А вот облака нижнего яруса (ниже 2 км) состоят преимущественно из водяных капель. Именно они являются основными «поставщиками» дождей. Поэтому для метеорологов так важно уметь определять высоту облаков.
6 – 2 км) скапливаются из мельчайших капель и кристаллов льда. А вот облака нижнего яруса (ниже 2 км) состоят преимущественно из водяных капель. Именно они являются основными «поставщиками» дождей. Поэтому для метеорологов так важно уметь определять высоту облаков.
Задача: придумайте способ нахождения высоты нижней границы облаков.
Рисунки проецируются на интерактивную доску.
Класс разбит на четыре микрогруппы: каждая группа ребят – представители одной из «Профессии» (геодезисты, инженеры проходчики, географы – метеорологи, этнографы-историки).
Каждой группе в зависимости от их профиля дается прикладная или практическая задача, решить которую необходимо за 8 минут.
Ученики:
переводят задачу на математический язык (моделируют ситуацию, изображают чертеж);
решают задачу в рамках полученной математической модели;
переводят полученный результат на первоначальный язык задачи.
Работа выполняется каждым учеником группы в тетради.
Учитель:
направляет работу учеников.
Защита: от каждой группы представитель объясняет решение, дает обоснование. Группа оценивается учителем и учениками, результаты выставляются в оценочный лист
5
Информационно-обобщающий. О значении теоремы Пифагора:
Оказывается, за долго до Пифагора она была известна египтянам, вавилонянам, китайцам и индийцам. Индийцы использовали ее для построения алтарей, которые по священному предписанию должны иметь геометрическую форму, ориентированную относительно четырех сторон горизонта. Доказательство самого Пифагора до нас не дошло. В настоящее время имеется более ста различных доказательств этой теоремы. Значение теоремы состоит в том, что из нее или с ее помощью можно вывести большинство теорем геометрии. Доказательство теоремы учащиеся средних веков считали очень трудным и называли его «Ослиный мост» или «Бегство убогих», так как некоторые «убогие» ученики, не имевшие серьезной математической подготовки, «бежали» от геометрии. Ученики рисовали шаржи на теорему Пифагора. Существует легенда о том, что в честь своего открытия Пифагор принес в жертву быка или, как рассказывают другие, сто быков. Поэты сочиняли стихи об этой теореме. Например, А. Шамиссо писал:
Прибудет вечной истина, как скоро
Ее познает слабый человек!
И ныне теорема Пифагора, верна
Как и его далекий век!
Двое учащихся заранее готовит сообщение. Теорема Пифагора – одна из главных теорем геометрии.
Рассказ учащихся сопровождается показом слайдов ( см. приложение 1-5
Учитель благодарит учеников за содержательную информацию.
6
Подведение итогов урока
а) какие знания нам понадобились при решении задач данного типа?
б) о чем надо помнить, применяя теорему Пифагора?
в) достигли ли мы цели урока?
Самооценка по основным видам работ (см. оценочный лист
Учитель дает общую оценку работе на уроке.
Выставляет отметки
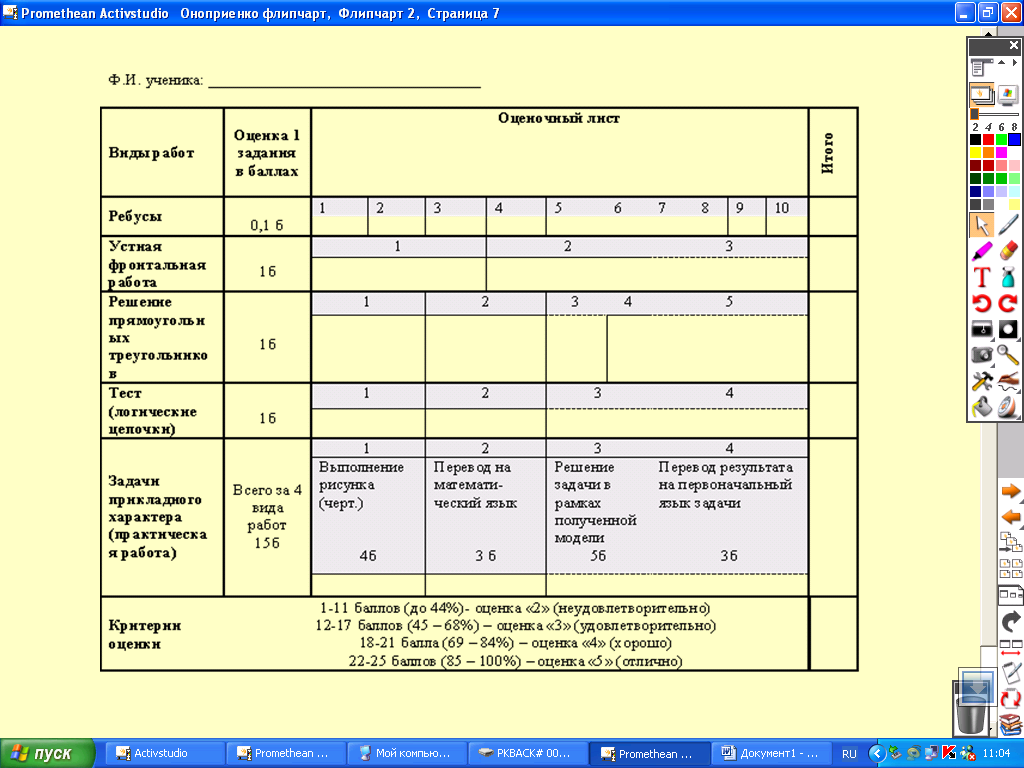
Оценочный лист
7
Постановка домашнего задания
Конкурс на лучший мини-проект на тему: «Астана в геометрических образах» презентация в программе Power Point. (Срок выполнения 1 месяц)
Задачи приладного характера:
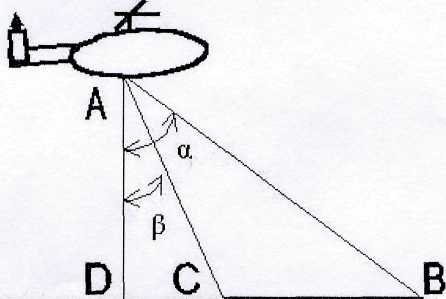
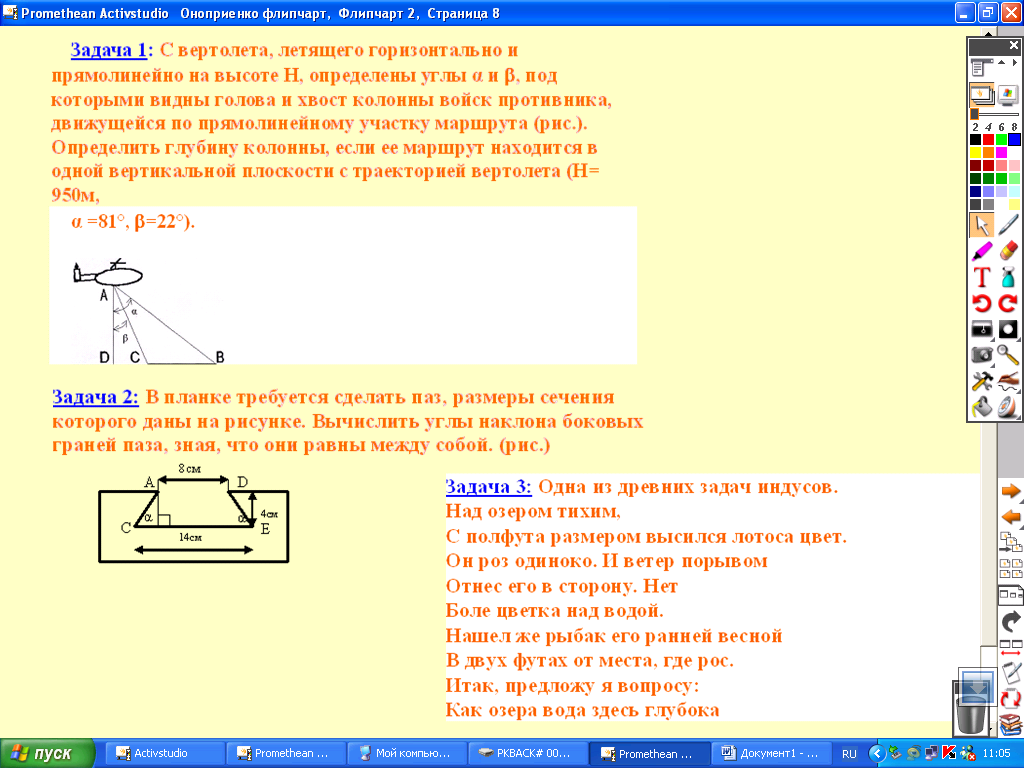
Задача 1: С вертолета, летящего горизонтально и прямолинейно на высоте Н, определены углы α и , под которыми видны голова и хвост колонны войск противника, движущейся по прямолинейному участку маршрута (рис. 8). Определить глубину колонны, если ее маршрут находится в одной вертикальной плоскости с траекторией вертолета (Н= 950м,
α =81°, =22°).
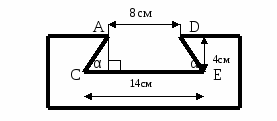
Задача 2: В планке требуется сделать паз, размеры сечения которого даны на рисунке. Вычислить углы наклона боковых граней паза, зная, что они равны между собой. (рис.)
Задача 3: Одна из древних задач индусов.
Над озером тихим,
С полфута размером высился лотоса цвет.
Он роз одиноко. И ветер порывом
Отнес его в сторону. Нет
Боле цветка над водой.
Нашел же рыбак его ранней весной
В двух футах от места, где рос.
Итак, предложу я вопросу:
Как озера вода здесь глубока
Урок завершается вручением каждому ученику небольшого сюрприза: открытка с одним из пожеланий:
научиться преодолевать трудности.
справляться с любыми задачами.
получить за III четверть 5 по математике
выполнять все домашние задания только на 5.
стать отличником по всем предметам.
быстрее всех решать самые трудные задачи.
побеждать на олимпиадах.
быть творческой личностью.
развивать исследовательские навыки.
принять участие в конкурсе гениальных проектов.
Учитель объявляет конкурс на лучшую презентацию мини-проекта (пространственные аналоги треугольника).
Предложенные задачи прикладного характера должен решить каждый ученик, оформив решение в тетради.
Учитель демонстрирует условие каждой задачи на интерактивной доске.
Каждый ученик получает карточки с домашним зданием
Открытки с сюрпризом вручаются каждому ученику.
Приложение 2
Найдите неизвестные стороны треугольников.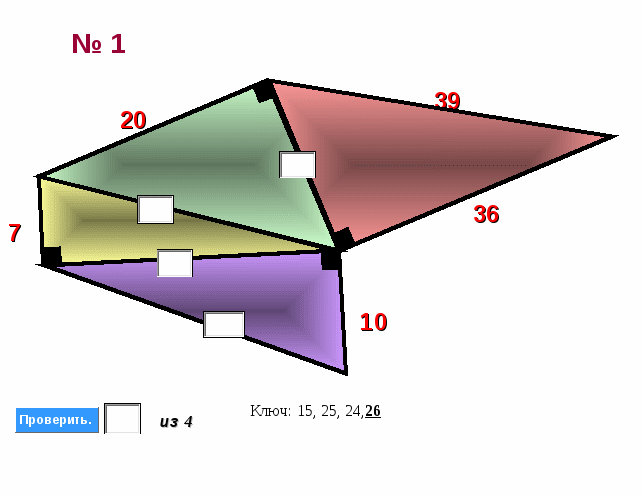

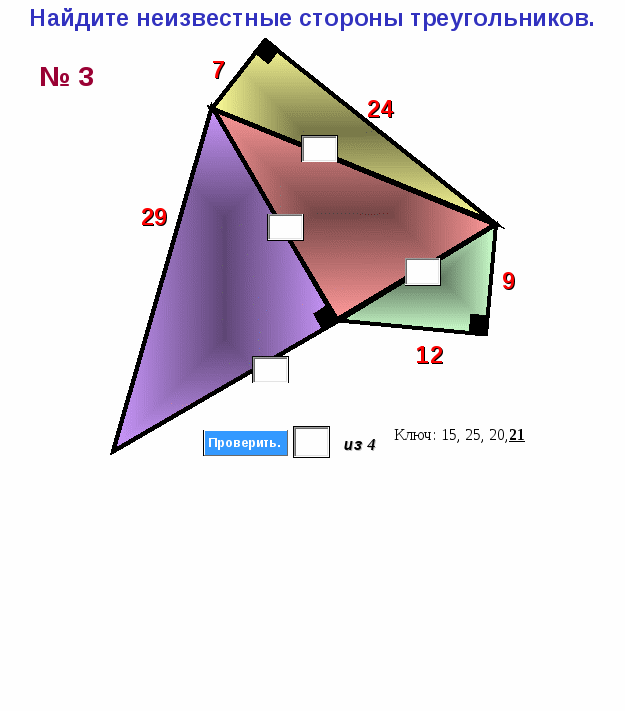
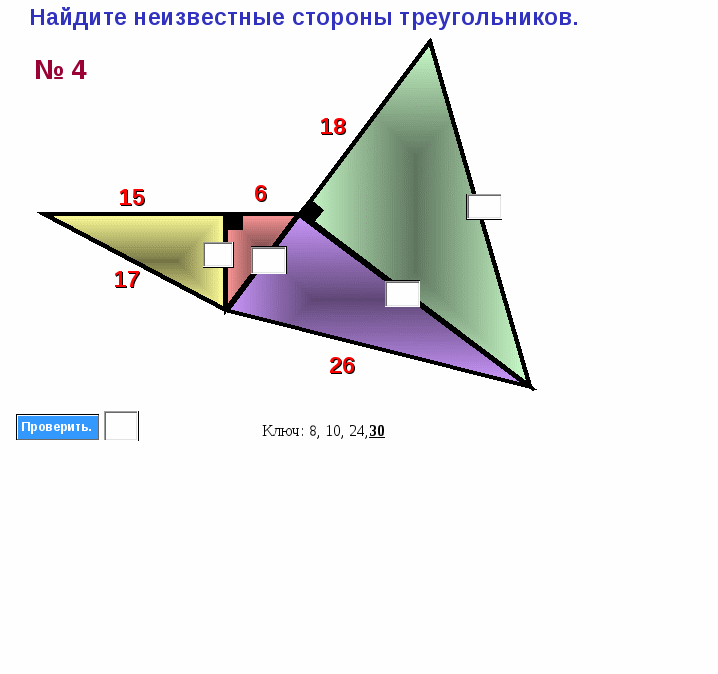
Приложение 3
Ф.И. ученика: __________________________________
Виды работ
Оценка 1 задания
в баллах
Оценочный лист
Итого
Ребусы
0,1 б
1
2
3
4
5
6
7
8
9
10
Устная фронтальная работа
1б
1
2
3
Решение прямоугольных треугольников
1б
1
2
3
4
5
Тест (логические цепочки)
1б
1
2
3
4
Задачи прикладного характера (практическая работа)
Всего за 4 вида работ
15б
1
2
3
4
Выполнение рисунка (черт.)
Перевод на математи-ческий язык
Решение задачи в рамках полученной модели
Перевод результата на первоначальный язык задачи
4б
3 б
5б
3б
Критерии оценки
1-11 баллов (до 44%)- оценка «2» (неудовлетворительно)
12-17 баллов (45 – 68%) – оценка «3» (удовлетворительно)
18-21 балла (69 – 84%) – оценка «4» (хорошо)
22-25 баллов (85 – 100%) – оценка «5» (отлично)



Нравится материал? Поддержи автора!
Ещё документы из категории геометрия:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ