Конспект урока по Геометрии "Треугольники. Признаки равенства треугольников" 7 класс
РАЗРАБОТКА УРОКА по геометрии 7 класс: « Треугольники. Признаки равенства треугольников». Выполнила учитель 2 категории Петракова Е.Н.(Саратовская обл., Саратовский р-он. МОУ СОШ п.Расковр.) Цели урока: Образовательные:
организовать деятельность учащихся по применению знаний при решении задач на применение элементов треугольника; признаков равенства треугольников.
развитие ключевых компетенций:
формирование способности к оцениванию собственной деятельности.
создать условия для :
формирования интереса учащихся к математике через углубление их представлений о практическом значении треугольников и применении их в окружающем мире;
развитие деловых качеств личности, личностного самосовершенствования.
Развивающие:
способствовать развитию наблюдательности, умению анализировать,
сравнивать и делать выводы;
развитие логического мышления, математической речи, интереса учащихся к изучению геометрии;
Воспитательные:
повысить интерес к нестандартным задачам;
способствовать формированию активности.
Задачи урока:
учить учащихся грамотно вести монологическую речь;
учить самостоятельной работе учащихся с различными источниками информации;
Тип урока:
Урок обобщения и систематизации знаний, умений и навыков.
Необходимое оборудование и материалы:
компьютер;
экран.
Структура урока:
Организационный момент.
Постановка учебной проблемы.
Актуализация опорных знаний. Работа по готовым чертежам.
Обобщение и систематизация ключевых понятий.
Закрепление навыков решения практических задач.
Применение изучаемой темы в природе.
Задание на дом.
Подведение итогов урока.
Ход урока:
1. Организационный момент.
Дорогие ребята! Я надеюсь, что этот урок пройдет интересно, с большой пользой для всех.
Уверена, что на сегодняшнем уроке вы будете активны, внимательны, и получите знания, которые пригодятся вам в дальнейшей жизни.
2. Постановка учебной проблемы.
Учитель: В геометрии среди множества различных фигур на плоскости выделяется большое семейство многоугольников. Сегодня мы закончим изучение одного вида многоугольников, решив кроссворд, вы узнаете тему нашего урока.
Вопросы и ответы к кроссворду:
Перпендикуляр, опущенный из вершины треугольника к прямой, содержащий противоположную сторону (высота).
Часть прямой , имеющая начало и конец (отрезок).
Отрезок, соединяющий вершину треугольника с серединой противоположной стороны треугольника (медиана).
Что измеряют транспортиром (углы).
Единица измерения углов (градус).
Какой школьный предмет изучает многоугольники (геометрия).
Прибор для измерения длины( линейка).
Прибор для построения окружности (циркуль).
Треугольник , у которого все стороны равны(равносторонний).
10.Сумма всех сторон треугольника (периметр).
11.Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны (биссектриса).
И так. Ключевое слово треугольник. И тема нашего урока «Треугольник». Как вы думаете, на какие вопросы вы должны знать ответ, изучая тему «Треугольники»?
Учащиеся ставят проблемные вопросы и отвечают на них:
Что называется треугольником?
Сколько элементов содержит треугольник?
Какие отрезки называются медианой, биссектрисой и высотой треугольника?
Какие виды треугольников бывают? (по углам и сторонам)
Какими свойствами обладает равнобедренный треугольник?
Какие треугольники называются равными?
Признаки равенства треугольников.
Учитель: мы должны определить сферы практического использования знаний по данной теме.
3. Актуализация опорных знаний. Работа по готовым чертежам.
Задание 1. На рисунке МP =MT, PK=TK какие точки достаточно соединить, чтобы получились равные треугольники?
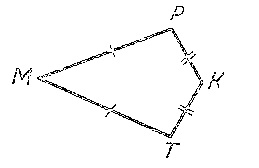
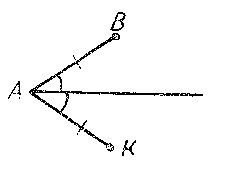
Задание 2. Проведите отрезок так, чтобы получились равные треугольники.
Проведите два отрезка так, чтобы получились равные треугольники.
Задание 3. На рисунке даны две окружности с общим центром О и равные отрезки АВ и СD. Какие пары точек достаточно соединить, чтобы получились равные треугольники?
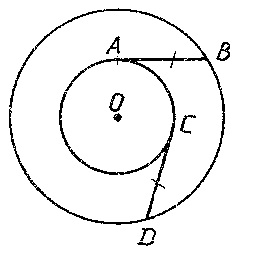
4. Обобщение и систематизация ключевых понятий.
Задача: На рисунке изображены два равных треугольника: АВС=ВАD. Докажите, что АОС= ВОD.
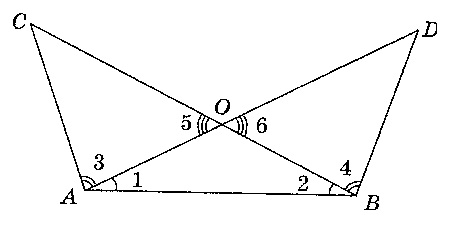
Учитель: Ребята, исходные данные у всех были одинаковыми, и цель у всех была одна. А вот пути решения были разными. Давайте их рассмотрим.
Учащиеся указывают различные способы доказательства. Наиболее быстрый способ записываем на доске.
5.Закрепление навыков решения практических задач.
Самостоятельная работа:
1.ОД-биссекриса угла АОВ, ДО-биссектриса угла АДВ.
Доказать: ОА=ОВ, ДА=ДВ.
2.АО-биссектриса угла ВОС.
Доказать: АОВ=АОС.
Учитель:
Ребята, сейчас в своей работе вы использовали такой приём, как – доказательство. Эта форма работы вам ещё недостаточно хорошо известна.
А до VI века н.э. с доказательством люди вообще были не знакомы.
Первым, кто начал получать новые геометрические факты при помощи рассуждений (доказательств), был древнегреческий математик Фалес, который жил в VI в. До н. э. (сообщение.)
Ему принадлежит открытие следующих теорем:
Вертикальные углы равны.
В равнобедренном треугольнике углы, лежащие при основании, равны.
Теорема о равенстве двух треугольников по стороне и двум прилежащим к ней углам.
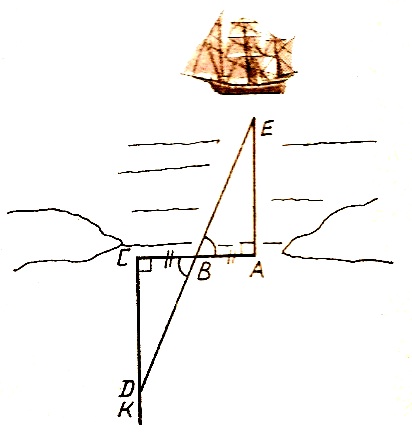
В гавани Милета был построен дальномер, определяющий расстояние до корабля в море. Он представлял собой три вбитых колышка А, В, С, (АВ = ВС ) и размеченную прямую . При появлении корабля на прямой СК находили точку D такую, чтобы точки D, В, Е оказывались на одной прямой. Как ясно из чертежа, расстояние на земле СD и является искомым расстоянием до корабля АЕ по воде.
Применение изучаемой темы в природе.
Учитель: В нашей местности много озер. Решение следующей задачи позволит вам научиться определять ширину любого озера.
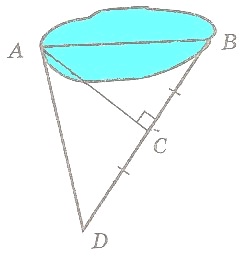
Задача: Чтобы измерить длину озера (расстояние АВ на рисунке) на местности провели прямою ВD, на ней выбрали точку C, из которой точка А видна под прямым углом, и отложили отрезок СD, равный отрезку ВC. Какое расстояние на местности надо измерить, чтобы узнать длину озера?
Ответ:
Для этого достаточно измерить длину отрезка АD, так как АСD=ВСА (по первому признаку).
Учитель: При изучении данной темы вы познакомились с понятием равнобедренного и равностороннего треугольника. Ответим на вопрос: Чем удивителен треугольник?
А ведь знакомый всем нам треугольник также таит в себе немало интересного и загадочного.
В чем уникальность равнобедренного и равностороннего треугольника?
Учитель: Математика связана с красотой окружающего нас мира. Например, мир природы и симметрии. Искусство и математика, в частности архитектура, скульптура, изобразительное искусство. Вашему вниманию будет представлена с одной стороны простая, а с другой очень интересная и красивая геометрически, а также интересная и для науки геометрическая система, которая состоит из равнобедренных и равносторонних треугольников.(слайд).
Учитель: А где же еще можно увидеть применение треугольников?
Сообщение о пирамидах.
Учитель: Конечно, все законы красоты невозможно вместить в несколько формул, но, изучая математику, мы можем открыть новые элементы прекрасного , которые находят свое применение в окружающем нас мире.
Вывод:
7.Задание на дом.
Учащимся предлагается дома
подготовить кроссворд.
8.Подведение итогов урока.
Учитель предлагает учащимся оценить уровень своих знаний по теме. Оценить сообщения. Учитель оценивает учащихся.
Рефлексия.
1.Доволен ли ты тем как прошел урок?
2.Было ли тебе интересно?
3.Сумел ли ты получить новые знания?

Нравится материал? Поддержи автора!
Ещё документы из категории геометрия:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ