Конспект урока по геометрии в 7 классе «Начальные геометрические сведения»
Тамбовское областное государственное автономное образовательное учреждение – общеобразовательная школа – интернат
«Мичуринский лицей»
Конспект урока по геометрии
в 7 классе
«Начальные геометрические сведения»
подготовила
учитель математики
Бобровская Мария Васильевна
Г. Мичуринск
2013год.
Обобщающий урок по геометрии в 7 классе
с элементами исследовательской работы.
Тема: Начальные геометрические сведения.
Тип: комбинированный, с применением компьютерных технологий.
Цель: повторение, обобщение и углубление изученного материала.
Задачи:
Образовательные-
обобщить и скорректировать знания по изученной теме.
Воспитательные-
воспитывать познавательную активность;
прививать учащимся интерес к предмету.
Развивающие –
развивать математически грамотную речь, умение выстраивать алгоритм геометрических рассуждений;
развивать творческую и мыслительную деятельность учащихся на уроке с помощью решения задач исследовательского характера;
развивать интеллектуальные качества учащихся такие, как самостоятельность, способность к оценочным действиям, обобщению, быстрому переключению;
способствовать формированию навыков самостоятельной работы и работы в группах.
План урока:
Вводное слово учителя с показом слайдов.
Повторение ранее изученного геометрического материала.
Проверка домашнего задания и решение дополнительной задачи.
Отчет групп учащихся о результатах исследований.
Проверка усвоения изученного материала. Тест.
Подведение итогов урока. Выставление оценок. Домашнее задание.
Ход урока
1. Вводное слово учителя.
Презентация, сопровождающая урок. Слайд 1 – 5.
2. Повторение изученного материала. Слайд 6.
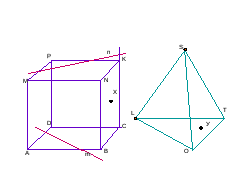
Учащимся предлагается ответить на вопросы (или можно предложить описать рисунки с использованием терминов – точка, прямая, луч, отрезок, угол, плоскость):
назовите прямые, изображенные на этих рисунках;
назовите точки;
каким плоскостям принадлежат точки Х, У, L, S?;
пересекаются ли прямые m, n, n и CK?;
с какими прямыми пересекается прямая n?
назовите параллельные прямые, перпендикулярные, скрещивающиеся прямые;
найдите вертикальные, смежные углы.
Слайд 7:
Давид Гильберт: «В огромном саду геометрии каждый найдет букет себе по вкусу».
Попробуем сегодня на уроке убедиться в этом…
Один из « букетов» приготовила к уроку группа учащихся, которая составила «Учебник – справочник» по данной теме. В нем не только справочный материал, но и разнообразные задачи по данной теме. Некоторые из них были предложены в качестве домашней работы к уроку. Дополнительные задачи из учебника-справочника:
Даны пять точек и прямая, не проходящая ни через одну из этих точек. Известно, что три точки расположены в одной полуплоскости относительно этой прямой, а две точки – в другой полуплоскости. Каждая пара точек соединена отрезком. Сколько отрезков пересекает прямую?
Может ли прямая, не проходящая ни через одну из вершин треугольника, пересекать каждую его сторону?
Отрезки АВ и СД, не лежащие на одной прямой, пересекаются в точке Е. Пересекает ли отрезок АС прямую ВД?
На одной стороне треугольника дано 3 точки, а на другой – 4. Сколько существует отрезков, соединяющих попарно эти 7 точек?
Сколько прямых проходит через различные пары из а) трех точек, б) четырех точек, в) пяти точек?
Какое наибольшее число точек попарных пересечений могут иметь а) три прямые; б) четыре прямые; в) пять прямых?
На сколько частей разбивает плоскость а) две прямые; б) три прямые; в) четыре прямые?
Как, не имея никаких измерительных средств, отмерить 50см от шнурка, длина которого 2/3 метра?
На линейке длиной 9см нет делений. Нанесите на нее три промежуточных деления так, чтобы можно было измерять расстояние от 1см до 9см с точностью до 1см.
Дан угольник, у которого есть ровно один угол в 19 градусов, а про остальные углы ничего не известно. Можно ли с его помощью отложить угол в 75 градусов?
На прямой отмечен отрезок АС и 45 точек, лежащих вне отрезка АС. Доказать, что сумма расстояний от этих точек до точки А не равна сумме расстояний до точки С.
Можно ли провести из одной точки на плоскости пять лучей так, чтобы среди образованных ими углов было, ровно четыре острых? Рассматриваются углы не только между соседними, но и между любыми двумя лучами.
Можно ли расставить на футбольном поле четырех футболистов так, чтобы попарные расстояния между ними равнялись 1, 2, 3, 4, 5 и 6 метров?
Есть три треугольника: остроугольный, прямоугольный, тупоугольный. Саша взял себе один треугольник, а Боря – два оставшихся. Оказалось, что Боря может приложить (без наложения) один из своих треугольников к другому, и получить треугольник, равный Сашиному. Какой из этих треугольников взял Саша?
Среди всех точек данной прямой с найти такую точку С, расстояние от которой до данной точки А, не принадлежащей прямой с, наименьшее. Существует ли точка Д на прямой с, для которой расстояние А наибольшее?
Дана прямая с и две точки А и В, не лежащие на этой прямой. Требуется найти такую точку С на прямой с, чтобы сумма расстояний АС+СВ была наименьшей.
Какое наибольшее число линий попарных пересечений могут иметь n плоскостей?
3. а) Проверка домашнего задания: Слайды 8 – 13.(Задачи с проверкой решения)
б) Слайд 14:
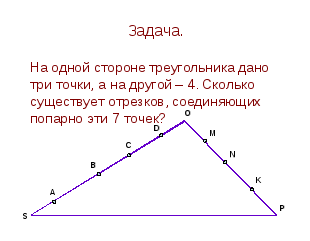
Эта задача (слайд 14) предлагается всем учащимся. Они решают ее, работая в парах. Обсуждается решение, и после этого рассматриваются результаты исследовательских работ групп учащихся. Это другие «букеты», составленные учащимися,
Работа велась учащимися в течение трех недель. Темы исследовательских работ: 1- «Взаимное расположение точек и прямых на плоскости», 2- «В мире многогранников».
4. Защита исследовательских работ. (Презентации учащихся).
5. Проверка усвоения изученного материала. Тест.
Тест « Начальные геометрические сведения»
Фамилия
Имя
Класс
Дата
1. Часть прямой, заключенная между двумя ее точками – это…
а) отрезок
б) полупрямая
в) луч
г) полуплоскость
2. Прямая разбивает плоскость на две…
а) полупрямых
б) плоскости
в) точки
г) полуплоскости
3.Часть плоскости, ограниченная двумя лучами с общим началом – это…
а) полуплоскость
б) прямая
в) угол
г) точка
4. Через две различные точки можно провести …
а) одну прямую
б) две прямых
в) сколько угодно прямых
г) ни одной прямой
5. Два угла, одна сторона которых общая, а другие стороны лежат на одной прямой, называются …
а) вертикальными
б) смежными
в) острыми
г) тупыми
6. Две прямые, пересекающиеся под прямым углом, называются …
а) перпендикулярными
б) пересекающимися
в) параллельными
г) непересекающимися
7. Точка С – середина отрезка АВ, а точка Д – середина отрезка АС. Какую часть отрезка ВД составляет отрезок АС? Ответ:
8. На прямой а отмечены три точки. Наименьший из образовавшихся при этом отрезков равен 3см. Может ли наибольший из отрезков иметь длину 5см? Ответ:
9. При пересечении двух прямых образовались четыре неразвернутых угла. Верно ли, что среди них обязательно найдется угол, который меньше суммы двух смежных с ним углов? Ответ:
Критерии оценивания:
№ задания
1
2
3
4
5
6
7
8
9
Количество балов
5
5
5
5
5
5
6
7
8
Выполнено
Оценка – «*» складывается из количества набранных балов.
Ключ:
а, г, в, а, б, а, 2/3, нет, да.
Учащиеся сами оценивают работы друг друга, обменявшись ими в парах, называют оценку.
Подведение итогов урока. Выставление оценок. Домашнее задание.
Решить из дополнительных задач №3, №10.(Задачи из учебника – справочника).
Рефлексия.
Учащиеся подводят итоги работы:
Усвоил и могу объяснить…
Усвоил…
Надо уточнить некоторые моменты…
Не понял…
Место урока при изучении материала первой главы по учебнику
Атанасян Л.С. и др. Геометрия 7-9. М.: Просвещение, 2011.
Перечень уроков по данной теме:
№
урока
Содержание учебного материала
Кол-во час.
Основные цели. Требования к математической подготовке учащихся.
ГЛ. 1
Начальные геометрические сведения.
13
Систематизировать знания учащихся об основных свойствах простейших геометрических фигур, ввести понятие равенства фигур.
1
Вводный урок «История возникновения и развития геометрии. Начальные геометрические сведения».
1
ЗУН: знать, свойства прямых, определение отрезка; уметь обозначать точки и прямые, изображать возможные случаи взаимного расположения точек и прямых, двух прямых, изображать и обозначать отрезки на рисунках, уметь находить прямые , отрезки, точки на изображениях пространственных тел.
2-3
Луч и угол. Решение задач исследовательского характера.
2
ЗУН: уметь объяснять, что такое луч, изображать и обозначать лучи на рисунке, знать определения угла, уметь его обозначать, называть элементы угла, знать и обозначать развернутый угол.
4
Сравнение отрезков и углов
1
ЗУН: знать определение равных фигур, середины отрезка, биссектрисы угла; уметь сравнивать отрезки и углы и записывать результаты сравнения, отмечать с помощью масштабной линейки середину отрезка, с помощью транспортира делить угол пополам и проводить биссектрису угла; сравнивать отрезки (ребра куба) на изображениях пространственных тел.
5-6
Измерение отрезков. Лабораторная работа №1
2
ЗУН: уметь измерять отрезок и выражать его длину в мм, см и т.д.; уметь решать задачи на нахождение длины отрезка по его частям и т. п.
7-8
Измерение углов. Лабораторная работа №2
Компьютерное тестирование «Вид и градусная мера угла»
2
ЗУН: уметь измерять данный угол, изображать прямой, острый, тупой, развернутый; уметь решать задачи на нахождение угла по его частям и т. п.; уметь находить такие углы на Рисунках с изображением пространственных тел.
9-10
Смежные и вертикальные углы. Лабораторная работа №3
и лабораторная работа №4
2
ЗУН: знать определения смежных, вертикальных углов, их свойства и применять их при решении задач; уметь изображать смежные, вертикальные углы, находить их на рисунке на плоскости и в пространстве;
11
Перпендикулярные прямые. Решение задач исследовательского характера.
1
уметь объяснять, почему две прямые, перпендикулярные третьей, не пересекаются; находить перпендикулярные прямые в пространстве.
12
Обобщающий урок
1
Решение задач исследовательского характера.
13
Тест
1
Проверка знаний изученной темы.
Используемые средства обучения:
Компьютер, мультимедийный проектор, экран, печатные средства (раздаточный материал).
Программные средства:
Microsoft Word
Microsoft Power Point
Internet Explorer
Ожидаемые результаты обучения:
Изучив тему «Начальные геометрические сведения» ученики должны:
Знать определения простейших геометрических фигур.
Понимать необходимость доказательства каждого утверждения.
Уметь выделять, из текста геометрической задачи, что дано и что требуется найти (доказать).
Отразить на рисунке и четко записать решение задачи.
Уметь находить простейшие геометрические фигуры в пространстве.
Список использованной литературы:
1.Атанасян Л.С. и др. Геометрия 7-9. М.: Просвещение, 2011.
2.Депман И.Я., Виленкин Н.Я. За страницами учебника математики. Пособие для учащихся 5-6 класса. М.: Просвещение, 1989.
3.Шарыгин И.Ф., Ерганжиева Л.Н. Наглядная геометрия. Учебное пособие для 5-6 классов. Смоленск: Русич, 1995.
4.Геометрия 7 класс. Поурочные планы по учебнику Атанасяна Л.С. и др. «Геометрия. 7-9 классы»./Авторы-составители Афанасьева Т.С., Тапилина Л.А. – Волгоград: Учитель, 2002.
5.Энциклопедия для детей. Том 11. Математика. – М.: Аванта +, 1999.
6. Васильев Н.Б. и др. Заочные математические олимпиады 2-е изд., перераб.— М.: Наука. Гл. ред. физ.-мат. лит., 1987.— 176с.
7.Смирнова И., Смирнов В.. Экстремальные задачи по геометрии М.: Чистые пруды, 2007. – 32 с. – (Библиотечка «Первого сентября», серия «Математика». Выпуск 2 (14)).
Интернет-ресурсы
1. http://festival.1september.ru/articles/subjects/1
2. http://www.ikt.oblcit.ru/8/perestoronina/urok_14.htm
3. http://rudocs.exdat.com/docs/index-18012.html

Нравится материал? Поддержи автора!
Ещё документы из категории геометрия:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ