Кривая Столетова

Ведерников А.И.

В предлагаемой статье рассматриваются характеристики магнитного поля. Строится предельно элементарная модель явления. При это автор исходит из феноменологического определения магнитной восприимчивости : ферромагнетики качественно олтличаются от пара и диамагнетиков тем, что в ферромагнетиках магнитные поля создаются не вследствии вращения электронов вокруг ядер, а вследжствие их собственного вращения. Электроны, вращаясь вокруг своей оси и обладая зарядом, создают магнитное поле наряду с полем, появляющимся за счет их орбитального движения вокруг ядра. Магнитная проницаемость µ у ферромагнетиков больше единицы: µ »1, при том, что µ=1+ (магнитная восприимчивость).

Иногда две большие темы пересекаются: 1) Тема математического анализа, как как структурообразующая тема, когда нахождение точек максимума, минимума и точек перегиба на графике позволяет судить о структуре. 2) Тема ферромагнетитков как упомянутая выше при том , что имеет место экспериментальная кривая (, Н), называемая кривой Столетова (график имеется в справочнике Б.М. Яворского и А.А. Детлафа).

Замечаем, что формулу

µ=1+

можно записать иначе, если иметь в виду, что для магнетиков, подчиняющихся зависимости



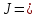
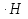
где 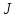– намагниченность, справедлива формула

)

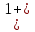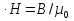
Так как 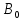= 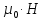то находим

=

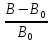Последнюю формулу можно представить в виде

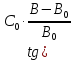)=1 (1)

Другими словами, можно подобрать такую постоянную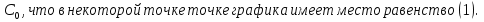

Идея применения матаматического анализа состоит в том, что угловой коэффициент касательной к некоторой кривой есть тангенс угла наклона этой касательной т.е. производная. Отсюда можно проедположить, что интегрируя производную, мы получим саму кривую Столетова, экспериментальная

µ

H

Кривая Столетова с теми структурными элементами (экстремумы, точки перегиба), что имеется у самой экспериментальной кривой.

Интегрируем

| +

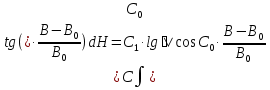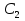
C_{1 –} постоянная, фиксирующая касательную по высоте.

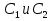– постоянные интегрирования . Но для того, чтобы такой подход

был корректным, необходимо сопоставление кривой Столетова с другим графиком. Для сопоставления возьмем петлю гистерезиса

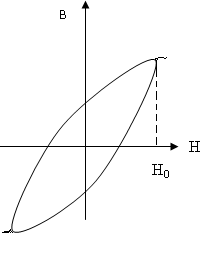
Из рассмотрения петли гистерезиса ясно видно почему H₀ не принадлежит графику на кривой Столетова теперь уже из физических соображений. Аналитическое выражение для петли гистерезиса теперь получается из аналитического выражения для кривой Столетова (2):

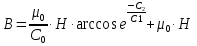
так как =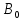

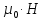
Подводя итог, мы должны обратить во внимание на два важных в этом выводе обстоятельства:

1) Мы исходим из того, что соотношение 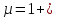является квантовым, поскольку квантовой механике не противоречит.

2) Для того, чтобы соотношение

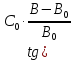)=1

выполнялось при любых B и B₀ необходимо , чтобы они были связаны функциональной зависимостью, в нашем случае петлей гистерезиса, что и делает наше рассмотрение корректным.