Урок по теме «Вычисление площадей с помощью интегралов»
Морозова Ирина Александровна
название работы – Урок по теме «Вычисление площадей с помощью интегралов»
предмет преподавания – Алгебра и начала анализа
автор учебника Алимов Ш. А. и др.
должность – учитель математики,
полное и точное наименование образовательного учреждения –
МОУ «Оброченская средняя общеобразовательная школа» Ичалковского района Республики Мордовия.
Тема: Вычисление площадей с помощью интегралов.
Цели: обобщить и систематизировать знания по теме «Первообразная»;
проведение тестирования с целью проверки знаний учащихся;
изучение формул нахождения площадей различных фигур;
отработка навыка нахождения площадей фигур, ограниченных графиками различных функций.
Ход урока:
Организационный момент.
Проверка д/з.
Повторение.
Устная работа.
Найти производную функции:
2x; 7x3; (2x – 5)4; 3 ln x; sin 2x.
Найти первообразную функции:
x7; 7x6; 1/x; sin 2x.
Тест.
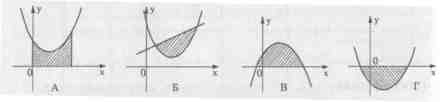
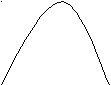
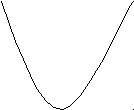
На каком рисунке изображена фигура, не являющаяся криволинейной трапецией?
С помощью формулы Ньютона-Лейбница вычисляют:
А. Первообразную функции;
Б. Площадь криволинейной трапеции;
В. Интеграл;
Г. Производную.
Найдите площадь заштрихованной фигуры.
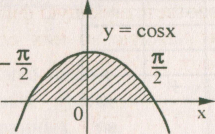
А. 0. Б. -2. В. 1. Г. 2.
![]()
Вычислите интеграл:
А. 1. Б. -1. В. -5. Г. 5.
![]()
А. 2a. Б. 2cos a. В. 0. Г. 2.
![]()
![]()
![]()
![]()
![]()
А. . Б. . В. . Г. .
Изучение нового материала.
На предыдущих уроках мы вычисляли площади криволинейных трапеций.
Какая фигура называется криволинейной трапецией?
Сегодня мы продолжим решать задачи на нахождение площадей различных фигур с помощью интегралов.
Как вычислить площадь фигуры, ограниченной линиями: y = f (x); y = 0; x = a; x = b.
-




a b
Выполнить записи в тетрадях.
Как вычислить площадь фигуры, ограниченной линиями: y = f (x); y = g (x); y = 0.
-
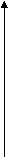

a
b
c
y=f(x)
y=g(x)

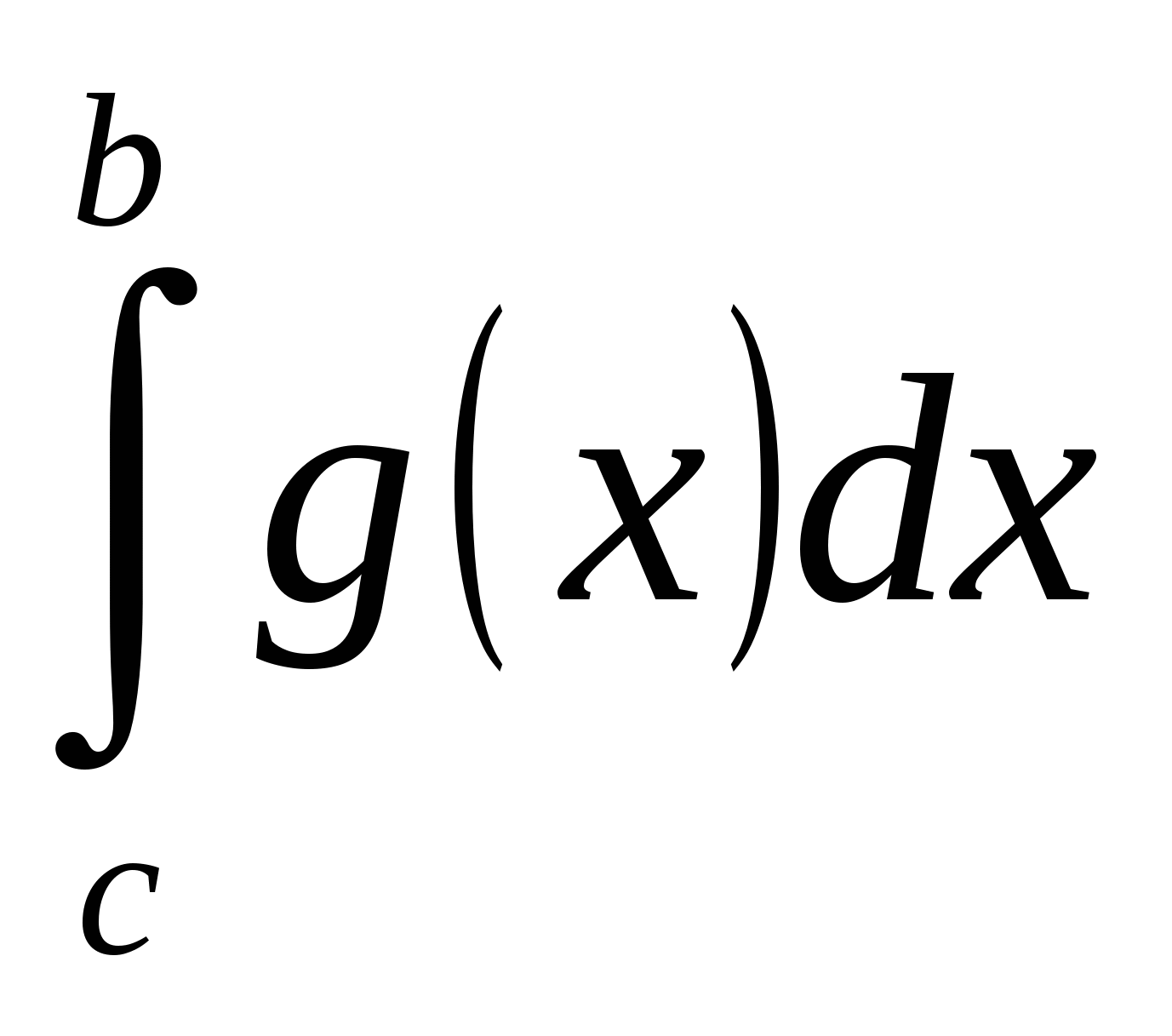

+
Как вычислить площадь фигуры, ограниченной линиями: y = f (x); y = 0; x = a; x = b
-
a b



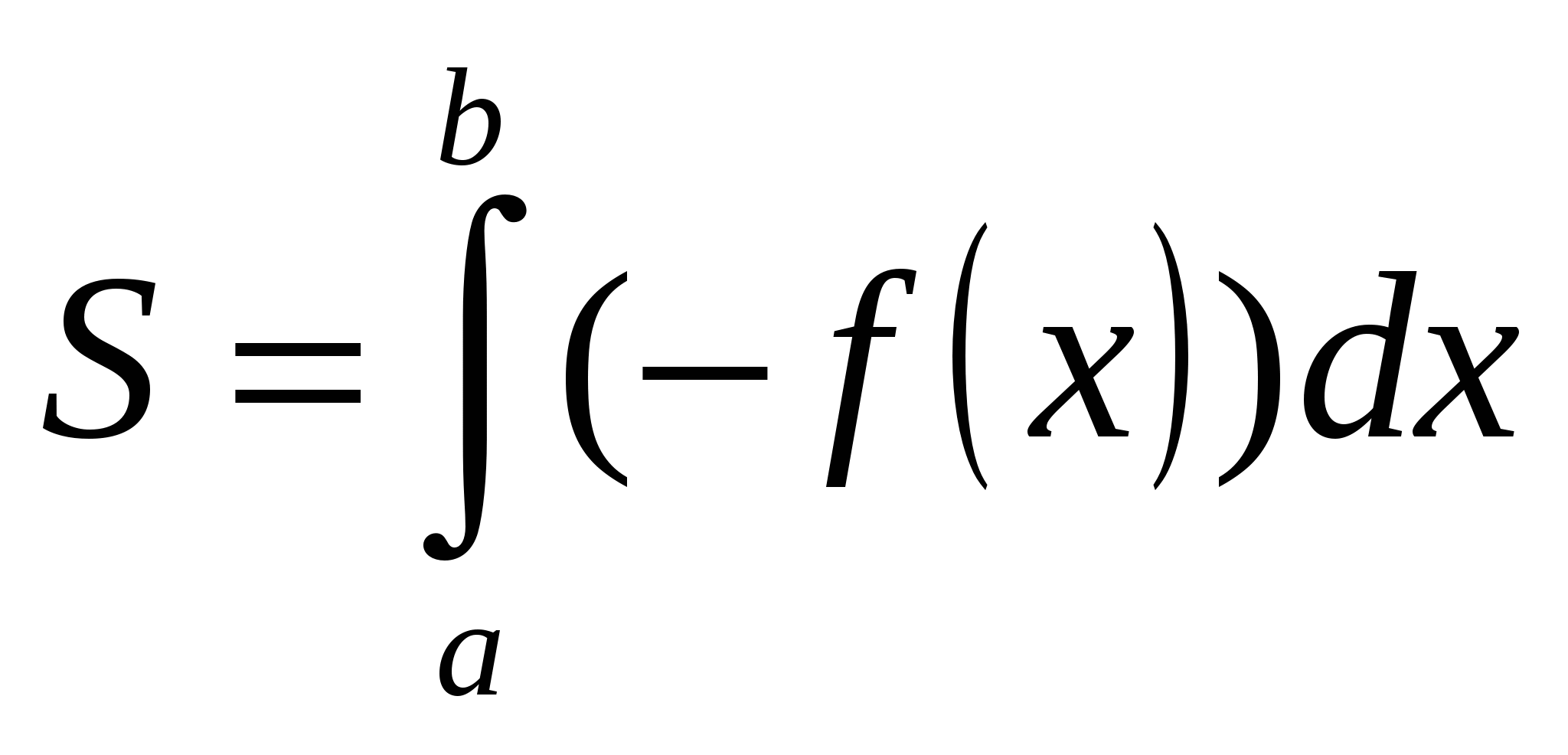
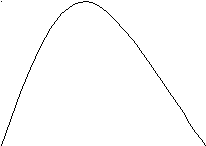
Как вычислить площадь фигуры, ограниченной линиями: y = f (x); y = g (x)
-

 y=f(x)
y=f(x)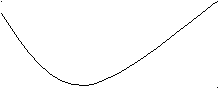
y=g(x)
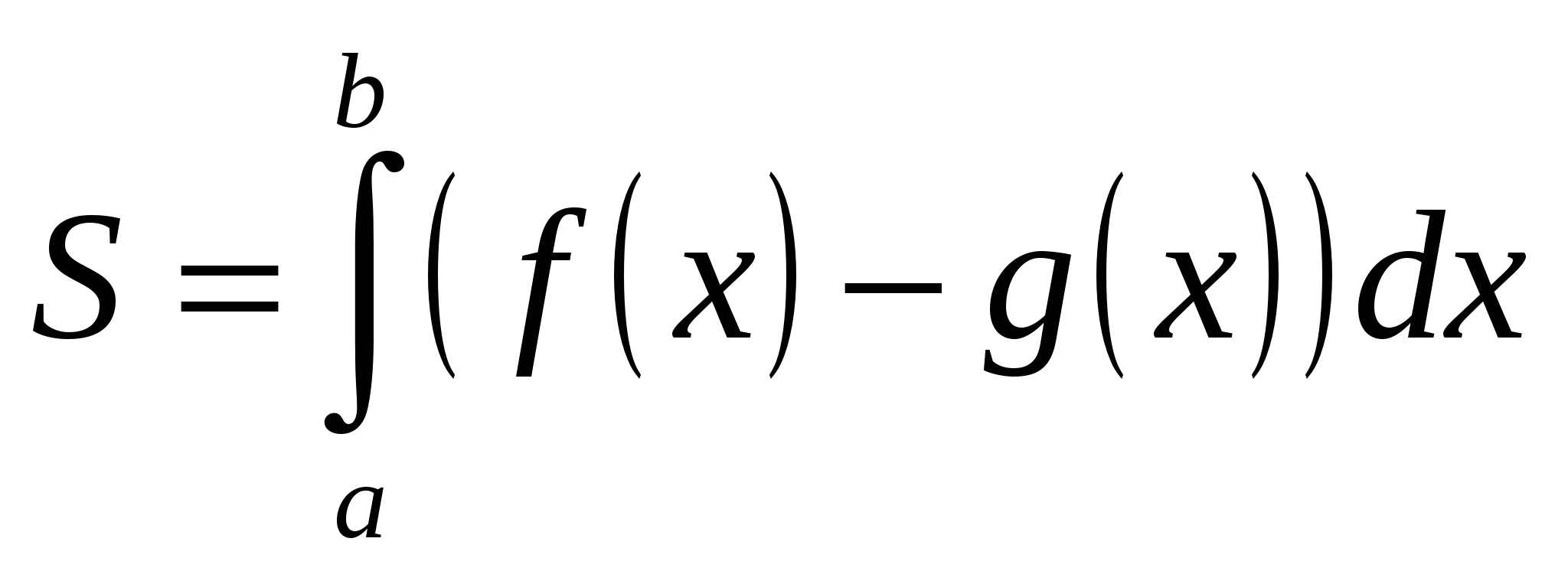
Решение заданий.
№ 1013(а) – учитель с классом
 S =
S = ![]()
№ 1013 (б,в) – на доске по очереди
Ответ: б) 1 2/3; в) 2 ln4.
№ 1014 (1) – на доске, (3) – самостоятельно с устной проверкой.
Итог урока.
Как вычисляется площадь криволинейной трапеции?
Какие из фигур, изображенных на рисунке, являются криволинейными трапециями?
Домашнее задание:
§ 58; № 1014(2; 4), 1034 (1; 3; 6), 1035(1; 2)

Нравится материал? Поддержи автора!
Ещё документы из категории геометрия:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ