Исследование кинетики реакции хлорирования бензола
Департамент науки и образования РФ
Московская государственная академия тонкой химической технологии
Домашняя работа
"Исследование кинетики реакции хлорирования бензола"
Выполнила студентка
группы БМ-54
Климук А.И.
Проверил
проф. Темкин О.Н.
Москва, 2005
ОПРЕДЕЛЕНИЕ ТЕКУЩИХ КОНЦЕНТРАЦИЙ ВЕЩЕСТВ
ОПРЕДЕЛЕНИЕ ПОРЯДКОВ РЕАКЦИИ ПО КОМПОНЕНТАМ
НАХОЖДЕНИЕ ВИДА ЗАВИСИМОСТИ ТЕКУЩИХ КОНЦЕНТРАЦИЙ ОТ ВРЕМЕНИ
ОПРЕДЕЛЕНИЕ ПОРЯДКОВ РЕАКЦИЙ МЕТОДОМ НАЧАЛЬНЫХ СКОРОСТЕЙ
ОПРЕДЕЛЕНИЕ ВИДА КИНЕТИЧЕСКОЙ МОДЕЛИ ИНТЕГРАЛЬНЫМ МЕТОДОМ
ОПРЕДЕЛЕНИЕ ЗНАЧЕНИЯ КОНСТАНТЫ СКОРОСТИ МЕТОДОМ НАИМЕНЬШИХ КВАДРАТОВ
СТАТИСТИЧЕСКАЯ ОБРАБОТКА ПОЛУЧЕННОЙ КИНЕТИЧЕСКОЙ МОДЕЛИ
ФОРМУЛЫ ДЛЯ РАСЧЕТА СТАТИСТИКИ (٭ )
Расчет дисперсии воспроизводимости
Расчет дисперсии неадекватности
Критерий Фишера.
Анализ коэффициентов
Расчет дисперсии остаточной
Подбор подходящего механизма реакции
СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ
Определение текущих концентраций веществ
По закону сохранения вещества:
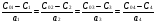 ,
,
где аi - стехиометрические коэффициенты соответствующих веществ в уравнении реакции;
Сi - концентрации соответствующих веществ.
Концентрация хлора (С2) поддерживается постоянной, поэтому имеем следующую таблицу значений текущих концентраций бензола (С1) и хлорбензола (С3):
С02=0,3
С02=0,9
Т, мин
C1, моль/л
С3, моль/л
C1, моль/л
С3, моль/л
C1, моль/л
С3, моль/л
C1, моль/л
С3, моль/л
C01=6
С03=0
С03=0
С03=0
С01=6
С03=0
12
5,925
0,075
5,927
0,073
5,928
0,072
5,931
0,069
24
5,86
0,14
5,853
0,147
5,859
0,141
5,854
0,146
36
5,79
0,21
5,778
0,222
5,784
0,216
5,798
0, 202
48
5,731
0,269
5,711
0,289
5,726
0,274
5,718
0,282
60
5,643
0,357
5,667
0,333
5,638
0,362
5,662
0,338
72
5,57
0,43
5,566
0,434
5,574
0,426
5,598
0,402
96
5,469
0,531
5,455
0,545
5,46
0,54
5,425
0,575
120
5,344
0,656
5,308
0,692
5,324
0,676
5,31
0,69
С02=0,6
С01=6
13
5,921
0,079
26
5,844
0,156
39
5,763
0,237
52
5,699
0,301
65
5,61
0,39
78
5,572
0,428
104
5,425
0,575
130
5,287
0,713
С02=0,6
С01=4
20
3,92
0,08
40
3,837
0,163
60
3,76
0,24
80
3,685
0,315
100
3,626
0,374
120
3,565
0,435
160
3,419
0,581
200
3,247
0,753
С02=0,6
С01=2
43
1,92
0,08
Продолжение таблицы.
86
1,827
0,173
129
1,766
0,234
172
1,692
0,308
215
1,616
0,384
258
1,557
0,443
344
1,426
0,574
430
1,328
0,672
С02=0,6
Т, мин
С01=6
6
5,927
0,073
12
5,86
0,14
18
5,78
0,22
24
5,715
0,285
30
5,647
0,353
36
5,573
0,427
48
5,425
0,575
60
5,316
0,684
Определение порядков реакции по компонентам
Для нахождения порядков реакции можно использовать разные методы. Воспользуемся, например, методом начальных скоростей. Для этого необходимо найти начальные скорости. С этой целью проведем статистическую обработку экспериментальных данных для выявления вида зависимости текущих концентраций веществ от времени. Затем, продифференцировав по времени, получим выражение для скорости реакции.
Нахождение вида зависимости текущих концентраций от времени
Экспериментальные данные по текущим концентрациям приведены для продукта реакции – хлорбензола (С3), поэтому поиск модели будем проводить на их основе.
Рассмотрим первые три опыта, т. к. они отвечают требованию воспроизводимости.
Опишем зависимость концентрации хлорбензола (С3) от времени полиномом 1 степени:
Матрица Х:
1
12
1
24
1
36
1
48
1
60
1
72
1
96
1
120
Матрица Хт:
1
1
1
1
1
1
1
1
12
24
36
48
60
72
96
120
Ковариационная матрица
0,491329
-0,00626
-0,00626
0,000107
Матрица(ХтХ) - 1Хт
0,416185
0,34104
0,265896
0, 190751
0,1156069
0,0404624
-0,10982659
-0,2601156
-0,00498
-0,00369
-0,00241
-0,00112
0,0001606
0,0014451
0,00401413
0,0065832
Перемножив матрицы (ХтХ) - 1Хт и матрицу средних значений концентраций С3 по повторяющимся опытам, получим значения коэффициентов уравнения полинома.
Матрица В:
0,012624
0,005562
Т, мин
С3(1)
С3(2)
С3(3)
С3средн
C3 расч
12
0,075
0,073
0,072
0,073
0,079368
24
0,14
0,147
0,141
0,143
0,146112
36
0,21
0,222
0,216
0,216
0,212856
48
0,269
0,289
0,274
0,277
0,2796
60
0,357
0,333
0,362
0,351
0,346344
72
0,43
0,434
0,426
0,43
0,413088
96
0,531
0,545
0,54
0,539
0,546576
120
0,656
0,692
0,676
0,675
0,680064
Дисперсия воспроизводимости: Sy=0.00009925
Дисперсия неадекватности: Sнеад=0,000229
Критерий Фишера: F=2.305
Табличное значение Fт(6, 16) =3,2
F<Fт; модель адекватна.
Ошибка определения коэффициентов:
70,35924
1,03852
Коэффициент Стьюдента
5573,328
186,7177
Т>Tкр
Коэффициент Стьюдента табличный:
Ткр=2.31
Все коэффициенты уравнения значимы, модель адекватна.
Y=0.012624+0.005562
Проверим графически соответствие модели экспериментальным данным.
Для этого построим кривые зависимости текущих концентраций от времени и с помощью линии тренда найдем вид уравнения.
Данные для построения графиков.
№ опыта
1
2
3
5
Т, мин
С3, моль/л
С3, моль/л
С3, моль/л
С3, моль/л
12
0,075
0,073
0,072
0,069
24
0,14
0,147
0,141
0,146
36
0,21
0,222
0,216
0, 202
48
0,269
0,289
0,274
0,282
60
0,357
0,333
0,362
0,338
72
0,43
0,434
0,426
0,402
96
0,531
0,545
0,54
0,575
120
0,656
0,692
0,676
0,69
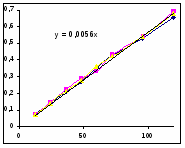
Константы в выражении, полученном графически, сравнимы с расчетными в уравнении полинома. Значения начальных скоростей примерно одинаковы. За истинные будем принимать расчетные значения.
Значение начальной скорости в рассматриваемом опыте: R0=0,0056 (моль/(л ч)).
Определим выражения для скоростей реакций по остальным опытам.
Рассчитанное выражение для зависимости концентрации хлорбензола от времени разобранным выше матричным методом:
МатрицаХ:
1
13
1
26
1
39
1
52
1
65
1
78
1
104
1
130
Матрица Хт:
1
1
1
1
1
1
1
1
13
26
39
52
65
78
104
130
Матрица Xт·X:
8
507
507
43095
Ковариационная матрица
0,491329
-0,00578
-0,00578
9,12E-05
Матрица (Xт·X) - 1·Xт:
0,416185
0,34104
0,265896
0, 190751
0,1156069
0,0404624
-0,10982659
-0,2601156
-0,00459
-0,00341
-0,00222
-0,00104
0,0001482
0,0013339
0,003705351
0,0060768
Матрица коэффициентов полинома В:
0,012624
0,005134
Т, мин
С3, моль/л
13
0,079
26
0,156
39
0,237
52
0,301
65
0,39
78
0,428
104
0,575
130
0,713
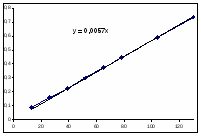
По уравнению кривой, построенной по экспериментальным данным, и расчетному выражению значения начальной скорости близки. Примем как более точное расчетное значение: R0=0,0051 (моль/(л ч)).
Определение выражения для скорости матричным методом. Для этого получим выражение для зависимости концентрации от времени и продифференцируем его по времени.
МатрицаХ:
1
20
1
40
1
60
1
80
1
100
1
120
1
160
1
200
Матрица Хт:
1
1
1
1
1
1
1
1
20
40
60
80
65
120
160
200
Матрица Xт·X:
8
780
745
98500
Ковариационная матрица
0,491329
-0,00376
-0,00376
3,85E-05
Матрица (Xт·X) - 1·Xт:
0,416185
0,34104
0,265896
0, 190751
0,1156069
0,0404624
-0,10982659
-0,2601156
-0,00299
-0,00222
-0,00145
-0,00067
9,634E-05
0,0008671
0,002408478
0,0039499
МатрицаВ:
0,013948
0,003627
Рассчитанное выражение для зависимости концентрации от времени:
Найдем графическое выражение.
Экспериментальные данные:
Т, мин
С3 эксп.
20
0,08
40
0,163
60
0,24
80
0,315
100
0,374
120
0,435
160
0,581
200
0,753
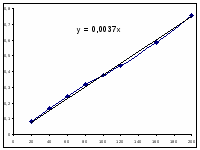
Значения начальных скоростей по графику и расчетное одного порядка, примем расчетное значение за истинное: R=0,0036 (моль/(л ч)).
Определение выражения для зависимости текущей концентрации от времени матричным методом.
Матрица Х:
1
43
1
86
1
129
1
172
1
215
1
258
Продолжение.
1
344
1
430
Матрица Хт:
1
1
1
1
1
1
1
1
43
86
129
172
65
258
344
430
Матрица Xт·X:
8
1677
1527
439245
Ковариационная матрица
0,491329
-0,00175
-0,00175
8,34E-06
Матрица(Xт·X) 1·Xт:
0,416185
0,34104
0,265896
0, 190751
0,1156069
0,0404624
-0,10982659
-0,260115
-0,00139
-0,00103
-0,00067
-0,00031
4,481E-05
0,0004033
0,001120222
0,0018372
Матрица коэффициентов полинома В:
0,037746
0,00153
Уравнение зависимости выглядит следующим образом:
Определение графическим способом.
Экспериментальные данные:
Т, мин
С3 эксп.
43
0,08
86
0,173
129
0,234
172
0,308
215
0,384
258
0,443
344
0,574
430
0,672
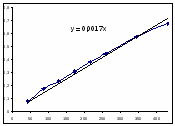
Значение начальной скорости: R=0,0015 (моль/(л ч)).
Нахождение вида зависимости концентрации от времени матричным способом.
Матрица Х:
1
6
1
12
1
18
1
24
1
30
1
36
1
48
1
60
Матрица Хт:
1
1
1
1
1
1
1
1
6
12
18
24
65
36
48
60
Матрица Xт·X:
8
234
269
10230
Ковариационная матрица
0,491329
-0,01252
-0,01252
0,000428
Матрица(XтX) 1Xт:
0,416185
0,34104
0,265896
0, 190751
0,1156069
0,0404624
-0,10982659
-0,260115
-0,00996
-0,00739
-0,00482
-0,00225
0,0003211
0,0028902
0,008028259
0,0131663
Матрица коэффициентов полинома В:
0,008006
0,011508
Графический метод.
Экспериментальные данные:
Т, мин
С3 эксп.
6
0,073
12
0,14
18
0,22
24
0,285
30
0,353
36
0,427
48
0,575
60
0,684
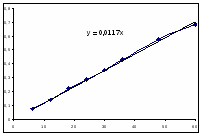
Выражение, полученное матричным методом:
Значение начальной скорости: R=0,0115 (моль/(л ч)).
Расчет матричным методом.
Матрица Х:
1
4
1
8
1
12
1
16
1
20
1
24
1
32
1
40
Матрица Хт:
1
1
1
1
1
1
1
1
4
8
12
16
65
24
32
40
Матрица Xт·X:
8
156
201
4980
Ковариационная матрица:
0,491329
-0,01879
-0,01879
0,000963
Матрица(Xт·X) 1·Xт:
0,416185
0,34104
0,265896
0, 190751
0,1156069
0,0404624
-0,10982659
-0,260115
-0,01493
-0,01108
-0,00723
-0,00337
0,0004817
0,0043353
0,012042389
0,0197495
Матрица коэффициентов полинома В:
0,011139
0,016717
Уравнение будет выглядеть:
Графический метод.
Экспериментальные данные:
Т, мин
С3 эксп.
4
0,073
8
0,142
12
0, 204
16
0,283
20
0,359
24
0,419
32
0,547
40
0,67
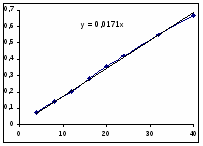
Значение начальной скорости: R=0,0167 (моль/(л ч)).
Определение порядков реакций методом начальных скоростей
Метод заключается в том, что строят графические зависимости LgR0=f(LgC0) или/и R0=f(C0) для опытов, где значения концентраций других компонентов, кроме исследуемого, одинаковы.
Ro
Co1
Co2
LgRo
lgCo1
lgCo2
Ck
LgCk
0,0056
6
0,3
-2,251812
0,7781513
-0,522878
0,1
-1
0,0056
6
0,6
-2,251812
0,7781513
-0,221848
0,1
-1
0,0051
6
0,9
-2,292429
0,7781513
-0,045757
0,1
-1
0,0036
4
0,6
-2,443697
0,60206
-0,221848
0,1
-1
0,0015
2
0,6
-2,823908
0,30103
-0,221848
0,1
-1
0,0115
6
0,6
-1,939302
0,7781513
-0,221848
0,2
-0,69897
0,0167
6
0,6
-1,777283
0,7781513
-0,221848
0,3
-0,522878
Определение порядка реакции по компоненту А1-бензол.
Ro
Co1
Co2
Ck
LgRo
lgCo1
0,0056
6
0,6
0,1
-2,251812
0,7781513
0,0036
4
0,6
0,1
-2,4436975
0,60206
0,0015
2
0,6
0,1
-2,8239087
0,30103
Зависимость LgR0=f(LgC01) Зависимость R0=f(C01)
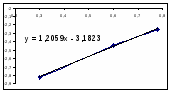
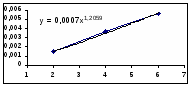
Порядок по компоненту А1 (бензолу) принимаем равным 1, т. к.1,2 примерно равно 1.
Определение порядка по катализатору.
Ro
Co1
Co2
Ck
LgRo
LgCk
0,0056
6
0,6
0,1
-2, 207608
-1
0,0115
6
0,6
0,2
-1,879426
-0,69897
0,0167
6
0,6
0,3
-1,790485
-0,522878
Зависимость R0=f(Ck) Зависимость LgR0=f(LgCk)
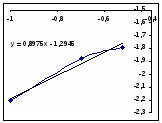
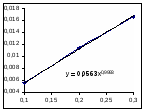
Порядок по катализатору примем равным 1.
Порядок по хлору определять не будем, т. к. его концентрацию поддерживают постоянной. Скорость реакции от него не будет зависеть.
Таким образом, вид кинетического уравнения для нашей реакции выглядит следующим образом:
Определение вида кинетической модели интегральным методом
Уравнение реакции:
C6H6(A1) + Cl2(A2) = C6H6Cl(A3) + HCl(A4)
d [A3] /dt = r = k [A1] [A2] = - d [A1] /dt
Проинтегрируем по t: - d [A1] / [A1] = k [A2] dt
ln [A1] 0 – ln [A1] = k [A2] t, т. к. концентрация хлора (А2) постоянна, выносим ее за знак интеграла.
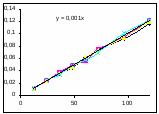 Ln([A1] 0/ [A1]) = k [A2] t, обозначим k [A2] Кнабл.
Ln([A1] 0/ [A1]) = k [A2] t, обозначим k [A2] Кнабл.
Определим графически значение Кнабл по всем опытам.
№опыта
1
2
3
5
Т, мин
Ln(C01/C1)
Ln(C01/C1)
Ln(C01/C1)
Ln(C01/C1)
12
0,0125788
0,0122413
0,012072581
0,0115666
24
0,0236099
0,0248051
0,023780529
0,0246343
36
0,0356272
0,0377019
0,036663984
0,0342464
48
0,0458694
0,0493653
0,046742263
0,0481404
60
0,0613436
0,0570996
0,062230077
0,0579823
72
0,0743644
0,0750828
0,07364654
0,0693501
96
0,0926637
0,0952268
0,094310679
0,1007416
120
0,115785
0,1225444
0,119534569
0,1221676
№опыта
4
6
7
8
Т, мин
Ln(C01/C1)
Т, мин
Ln(C01/C1)
Т, мин
Ln(C01/C1)
Т, мин
Ln(C01/C1)
13
0,0132541
20
0,020202707
43
0,040822
6
0,0122413
26
0,026344
40
0,04160355
86
0,0904719
12
0,0236099
39
0,0403013
60
0,061875404
129
0,1244301
18
0,0373558
52
0,0514687
80
0,082023835
172
0,1672359
24
0,0486652
65
0,0672087
100
0,098164249
215
0,2131932
30
0,060635
78
0,0740054
120
0,115130307
258
0,2503863
36
0,073826
104
0,1007416
160
0,15694625
344
0,3382739
48
0,1007416
130
0,1265085
200
0, 208562868
430
0,4094731
60
0,1210383
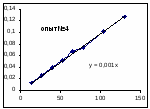
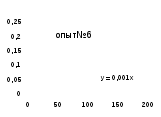
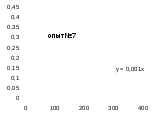
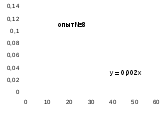
№опыта
9
Т, мин
Ln(C01/C1)
4
0,0122413
8
0,0239512
12
0,0345914
16
0,0483153
20
0,0616981
24
0,0723915
32
0,0955936
40
0,1184082
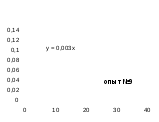
Как видно из уравнений прямых на диаграммах, значение Кнабл для всех опытов, кроме последних двух, одинаково и равно 0,001. Значит, в последних двух опытах действует какой-то другой параметр системы. Причем явно видно, что от концентрации хлора Кнабл совсем не зависит, т. к. для всех первых 7 опытов значение константы одинаково, но значение начальной концентрации хлора разное.
Если предположить, что в кинетическом уравнении вместо [A2] стоит суммарная концентрация катализатора, то тенденция в изменении Кнабл выглядит закономерной:
Кнабл
Ск
0,001
0,1
0,002
0,2
0,003
0,3
Определение значения константы скорости методом наименьших квадратов
Метод заключается в следующем:
R = k•C1•Ck∑
можно представить в виде уравнения прямой: у = Вх, где y=R, B=k, x=C1•Ck∑.
Домножая правую и левую часть уравнения у = Вх на х, получим квадратичное уравнение ух = Вх2.
Значение константы вычислим как: В = ух / х2.
№опыта
1
2
3
5
4
6
7
8
9
R
R
R
R
R
R
R
R
R
0,0056
0,0056
0,0056
0,0056
0,0051
0,0036
0,0015
0,0115
0,0167
С1•Сk
С1•Сk
С1•Сk
С1•Сk
С1•Сk
С1•Сk
С1•Сk
С1•Сk
С1•Сk
0,5925
0,5927
0,5928
0,5931
0,5921
0,392
0, 192
1,1854
1,7781
(С1•Сk) 2
(С1•Сk) 2
(С1•Сk) 2
(С1•Сk) 2
(С1•Сk) 2
(С1•Сk) 2
(С1•Сk) 2
(С1•Сk) 2
(С1•Сk) 2
0,351056
0,351293
0,351412
0,351768
0,350582
0,153664
0,036864
1,405173
3,16164
R•C1•Ck
R•C1•Ck
R•C1•Ck
R•C1•Ck
R•C1•Ck
R•C1•Ck
R•C1•Ck
R•C1•Ck
R•C1•Ck
0,003318
0,003319
0,00332
0,003321
0,00302
0,001411
0,000288
0,013632
0,029694
B=YX/X2
B=YX/X2
B=YX/X2
B=YX/X2
B=YX/X2
B=YX/X2
B=YX/X2
B=YX/X2
B=YX/X2
0,009451
0,009448
0,009447
0,009442
0,008613
0,009184
0,007813
0,009701
0,009392
Bсред= k =
0,00917
Среднее значение константы скорости по методу наименьших квадратов равно k=0,00917 [л/(моль•ч)]. Причем при умножении на Ск∑ значение константы, рассчитанное по методу наименьших квадратов, примерно совпадает со значением Кнабл, рассчитанным интегральным методом.
Статистическая обработка полученной кинетической модели
Для наилучшей обработки полученной модели проведем преобразование вида функции, т. к. зависимость скорости реакции от времени постоянна и для первых 3 опытов равна 0,0056. Скорость реакции получилась константа в результате дифференцирования по времени функции зависимости концентрации продукта реакции (хлорбензола) от времени.
1/С1= k•Ck/R
№ опыта
1
2
3
матрицаХ
1
2
3
C1
С1
С1
C1сред
Ск/R
1/C1
1/C1
1/C1
1/C1сред
Продолжение.
5,925
5,927
5,928
5,9267
17,8571
0,1732
0,1720
0,1720
0,1724
5,86
5,853
5,859
5,8573
17,8571
0,1761
0,1766
0,1768
0,1765
5,79
5,778
5,784
5,7840
17,8571
0,1727
0,1731
0,1729
0,1729
5,731
5,711
5,726
5,7227
17,8571
0,1745
0,1751
0,1746
0,1747
5,643
5,667
5,638
5,6493
17,8571
0,1772
0,1765
0,1774
0,1770
5,57
5,566
5,574
5,5700
17,8571
0,1795
0,1797
0,1794
0,1795
5,469
5,455
5,46
5,4613
17,8571
0,1809
0,1807
0,1813
0,1810
5,344
5,308
5,324
5,3253
17,8571
0,1813
0,1816
0,1817
0,1815
Обозначим Ck/R = Х, 1/С1 = У. Вычисления проводим, как описано выше.
Ковариационная матрица:
(XтX) - 1
0,000392
Полученная матрица коэффициента содержит 1 ячейку, где В= 0,0099.Т. е. значение константы скорости получили равным 0,0099 [л/(моль•ч)].
где k= 0,01 [л/(моль•ч)].
Статистическую обработку проводят по воспроизводимым опытам.
Значение дисперсии воспроизводимости Sвоспр= 1,41907∙10-7
Значение дисперсии неадекватности Sнеад= 3,14∙10-9;
Значение остаточной дисперсии Sост= 1,87∙10-9.
Критерий Фишера F= 3,1; табличное значение Ft= 3,2 для f1= 7, f2= 16. F<Ft – модель адекватна.
Формулы для расчета статистики (٭ )
Расчет дисперсии воспроизводимости
Предварительно считают дисперсию для каждого отдельного опыта:
Su2= (∑(yui-yсред) 2) /f,
где f2 = l-1 – число степеней свободы дисперсии воспроизводимости с учетом того, что 1 степень свободы потрачена на вычисление среднего значения;
l – число повторяющихся воспроизводимых опытов.
Среднее значение дисперсии воспроизводимости по всем опытам:
Sy2= ∑ Su2/n,
где n – число последовательных опытов.
В нашем случае l= 3, n= 8.
Расчет дисперсии неадекватности
S2неад= l∙(∑(yuрасч - yсред) 2) /(n-m)
где m – число коэффициентов модели.
n-m = f1 – число степеней свободы дисперсии неадекватности.
Критерий Фишера
F = S2неад / Sy2
Значение критерия Фишера расчетное сравнивают с табличным значением для соответствующих f1 и f2. Если F<Ft, то модель адекватна и производят дальнейший расчет значимости коэффициентов уравнения модели по критерию Стьюдента. Если модель неадекватна, то рассматривают другую модель.
Анализ коэффициентов
Производят оценку точности определения коэффициентов и анализ их значимости.
Дисперсия коэффициентов:
Sbj2= Cji Sy2
где Сji – диагональные элементы ковариационной матрицы.
Критерий Стьюдента:
tj = |bj| / √ Sbj2
Полученное значение критерия сравнивают с некоторым критическим значением, которое находят по таблице для числа степеней свободы f2. Если tj больше критического, то соответствующий коэффициент незначим и может быть исключен из уравнения. После исключения какого-то коэффициента анализ адекватности повторяют.
Расчет дисперсии остаточной
Soc2= (∑∑(yui – ycp) 2) / (nl – m)
Подбор подходящего механизма реакции
Допустим, что реализуется следующий механизм нуклеофильного замещения SN2:
Cl2 + FeCl3 → FeCl4 - + Cl+, k1
C6H6 + Cl+ → C6H5Cl + H+, k2
H+ + FeCl4-↔ FeCl3 + HCl, k3
Кинетическое уравнение для механизма SN2 выглядит следующим образом:
R = d [C6H5Cl] / dt = k2 [C6H6] [Cl+],
Скорость реакции по SN2 зависит от концентрации начального субстрата и нуклеофила. В качестве нуклеофила выступает частица Cl+.Т. к. концентрация хлора поддерживается постоянной, то ограничивающим фактором для количества образованной частицы Cl+ будет концентрация катализатора.Т. е. частиц Cl+ не может образоваться больше, чем присутствует в системе катализатора.Т. к. катализатор не образуется и не расходуется в системе, то в кинетическое уравнение войдет его суммарная концентрация.
Таким образом, получаем следующее кинетическое уравнение:
R = k2 [C6H6] [FeCl3] ∑, где [C6H6] = С1, [FeCl3] = Ск.
Первая стадия является лимитирующей.
Вид кинетического уравнения совпадает с выведенным по расчетам, значит, наш механизм является подходящим для описания эксперимента.
Список используемой литературы
1. К.Ю. Одинцов, Л.Г. Брук, О.Н. Темкин, "Статистическая обработка результатов кинетических исследований". – М.: МИТХТ, 2000, 52с.

Нравится материал? Поддержи автора!
Ещё документы из категории химия:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ