Моделирование стационарного и нестационарного истечения адиабатно-вскипающей жидкости из коротких каналов
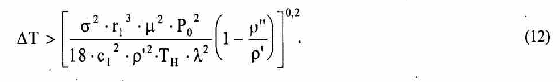

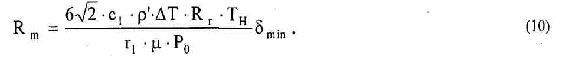
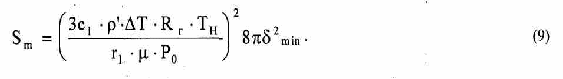





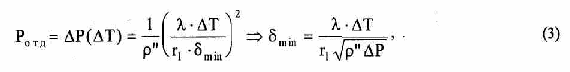
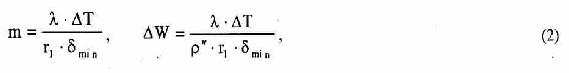

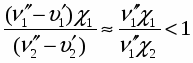
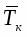
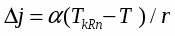
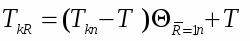
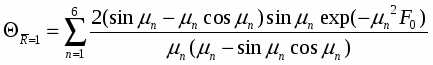
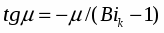
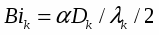
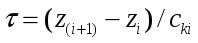
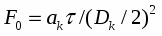
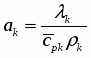
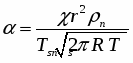
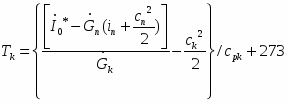
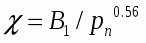
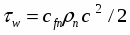
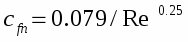
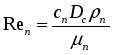
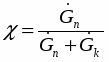
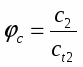
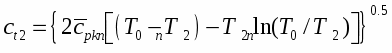
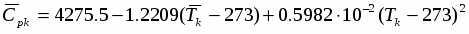
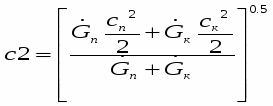
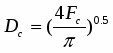
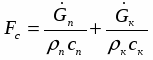
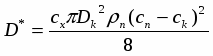
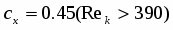
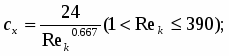
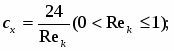
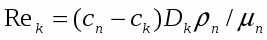
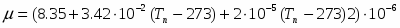
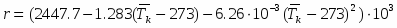
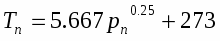
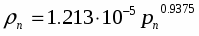
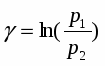
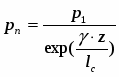
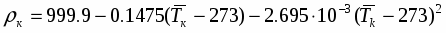
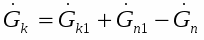
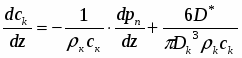
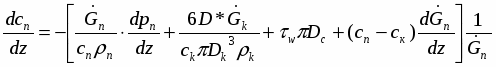
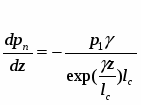
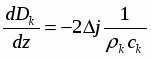
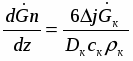
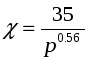
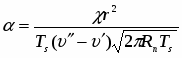
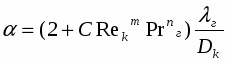





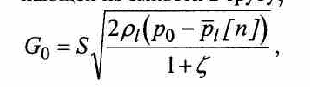
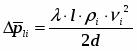


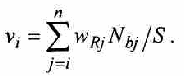
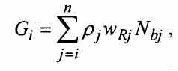













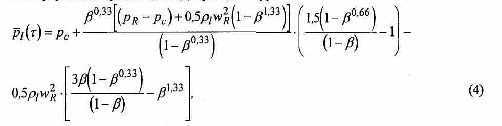

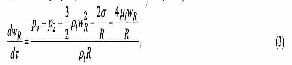

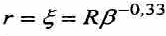
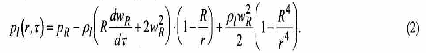
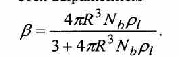
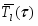 Моделирование стационарного и нестационарного истечения адиабатно вскипающей жидкости из коротких каналов
Моделирование стационарного и нестационарного истечения адиабатно вскипающей жидкости из коротких каналов
В работе [1] для анализа процесса нестационарного и стационарного истечения вскипающей жидкости в термодинамически неравновесном приближении использован нетрадиционный подход, в основу которого положена разработанная ранее модель, описывающая эволюцию ансамбля паровых пузырьков в процессе их интенсивного роста при быстром понижении внешнего давления /2,3/. Полученная информация положена в основу рассматриваемой здесь математической модели, которая по известным значениям температуры и давления перегретой жидкости на входе в канал истечения, по данным о геометрии канала и по значению давлению газа вне канала, позволяет рассчитать параметры парожидкостного потока пузырьковой структуры в любом сечении канала. Предполагается, что в рамках модели можно уточнить физическую сущность кризиса течения двухфазных потоков и прогнозировать критические параметры потока.
Принципиальным отличием модели является строгое выполнение условий термодинамической неравновесности. И температура и давление в жидкой и паровой фазах внутри канала различны, что позволяет рассмотреть как инерционную, так и термическую стадии роста пузырьков. В данной работе истечение вскипающей жидкости рассмотрено в односкоростном приближении. Модель допускает, однако, возможность учета относительного движения дисперсной паровой фазы в направлении движения потока, а также дробления пузырьков вследствие их динамического взаимодействия с окружающей жидкостью.
Модель динамики ансамбля паровых пузырьков
Математическая модель, прогнозирующая поведение ансамбля растущих или схлопывающихся паровых пузырьков, базируется на модели динамики одиночного пузырька. Принципы построения системы обыкновенных дифференциальных уравнений, описывающих динамику сферического парового пузырька в неограниченном объеме несжимаемой вязкой жидкости с учетом основных определяющих факторов, подробно изложены в работе (2). Эти уравнения дают возможность рассчитать радиус пузырька r(), давление и радиальную скорость жидкости на границе с пузырьком, соответственно, pr() = Pl(R, ) и wR() = wi(r, ), а также распределение скорости wl(r, ) и давления Pl(r, ) в окрестности пузырька. Кроме того, рассчитывается изменение температуры Tv(), плотности v() и давления пара pv() внутри пузырька. Предполагается, что эти параметры распределены в пузырьке однородно. Поток теплоты q() и массы j() через стенку пузырька в процессе испарения и конденсации пара описывается в приближении молекулярно -кинетической теории с учетом скачка температуры на межфазной границе T = Ts — Tv, так что в общем случае температура жидкости на границе с пузырьком Ts отлична от температуры пара в пузырьке Tv . Распределение температуры в жидкости в окрестности пузырька Tl (r, ) в процессе его роста или сжатия рассматривается в терминах интегрального метода, в рамках которого получено дифференциальное уравнение изменения толщины теплового пограничного слоя в жидкой фазе. В работе (2) приведены также полуэмпирические уравнения, которые с достаточно высокой точностью аппроксимируют температурные зависимости таких теплофизических параметров воды и водяного пара, как скрытая теплота испарения, поверхностное натяжение, плотность насыщенного пара, плотность и вязкость жидкости для всего температурного интервала существования жидкой фазы вплоть до Тсr. Достоверность модели подтверждается удовлетворительным согласием полученных с ее помощью расчетных результатов с известными в литературе экспериментальными данными по росту и схлопыванию одиночных паровых пузырьков в воде в широком интервале изменения режимных параметров.
Уравнения динамики одиночного пузырька положены в основу модели эволюции неограниченного монодисперсного ансамбля паровых пузырьков, которая учитывает динамическое взаимодействие пузырьков и их коллективное влияние на характер микротечений в межпузырьковом пространстве. Кроме основных уравнений динамики одиночного пузырька система уравнений, описывающих поведение ансамбля, включает дифференциальное уравнение для расчета средней температуры жидкости, которая не остается постоянной благодаря интенсивному испарению при формировании паровой фазы. Модель динамики пузырьков в ансамбле подробно рассматривается в работе (3). Предполагается, что динамическое развитие пузырьков в ансамбле обусловлено нарушением термодинамического равновесия вследствие быстрого изменения внешнего давления.
Поведение пузырьков в ансамбле рассматривается в приближении ячеечной модели, основные положения которой изложены, например, в работе [4]. Весь объем жидкости в монодисперсном пузырьковом ансамбле разбивается на идентичные сферические ячейки, в центре которых находятся сферические пузырьки. Радиус ячейки связан с величиной текущего паросодержания соотношением = R • -0.33 .Распределение давления зависит от текущих значений размера пузырьков и скорости их роста, а также от количества пузырьков в единице массы Nb, которое в отсутствие коагуляции или дробления пузырьков остается неизменным.
При заданной концентрации Nb величина объемного паросодержания определяется выражением
(1)
Для анализа поведения ансамбля в целом достаточно рассмотреть ситуацию в отдельной ячейке. При росте пузырька в его окрестности в пределах R ≤ r ≤ появляется сферически-симметричное распределение давления
(2)
Подстановка в (2) значения дает возможность найти давление в жидкости на внешней границе ячейки.
Когда пузырек находится в окружении других растущих пузырьков, поля давления ближайших соседей взаимно перекрываются и давление в любой точке межпузырькового пространства будет превышать внешнее давление, инициирующее рост или сжатие пузырьков. Поэтому поведение каждого отдельного пузырька в таком ансамбле должно определяться не внешним давлением рeх, действующим на систему в целом, а некоторым средним давлением в межпузырьковом пространстве > рeх. Как и для одиночного пузырька,в бесконечном объеме скорость радиального движения
(3)
за тем исключением, что в данном случае значение Р2 в (3) определяет не внешнее давление рeх, инициирующее рост пузырьков, а среднее давление в межпузырьковом объеме ансамбля pl (). Это среднее давление вычисляется путем интегрирования функции Pl(r,) по объему жидкости в ячейке и последующего деления на этот объем. Интегрирование правой части (2) приводит к уравнению
где рс определяет значение на предыдущем временном шаге расчета.
Усреднение относится как к отдельной элементарной ячейке, так и ко всему объему жидкости в пределах ансамбля. При использовании системы уравнений динамики одиночного пузырька это усредненное давление на каждом очередном шаге расчета определяет скорость изменения радиуса пузырька и значения теплофизических параметров системы, которые, в свою очередь, определяют на последующем шаге новое распределение давления в пределах ячейки и новое значение среднего давления в жидкости. Если термодинамическое равновесие в жидкости с пузырьками внезапно нарушено, например, вследствие резкого падения внешнего давления, наблюдается интенсивный рост паровой фазы. В начальный момент скорость расширения всех пузырьков определяется значением внешнего давления рex, а характер дальнейшего роста пузырьков ансамбля зависит от последующего изменения среднего давления .В результате давление в жидкой фазе асимптотически приближается к значению давления насыщения при данной температуре жидкости, но всегда остается меньше текущего давления пара внутри пузырька pv.
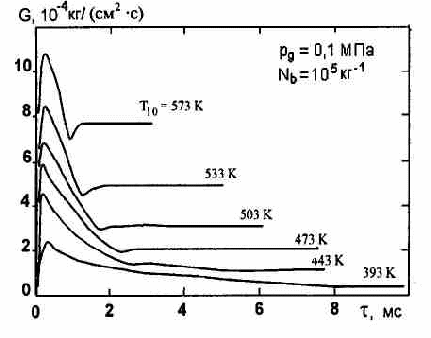
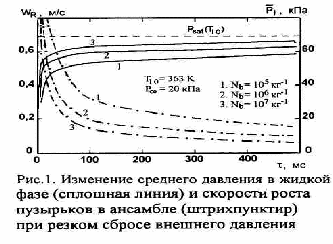
Поведение отдельного пузырька внутри ансамбля при тождественных условиях отличается от поведения одиночного пузырька в бесконечном объеме жидкости тем заметнее, чем сильнее проявляется фактор неодиночности пузырьков, т.е. чем выше концентрация Nb. На рис.1 показано, как меняются во времени среднее давление в межпузырьковом пространстве ансамбля и скорость расширения пузырьков после мгновенного сброса внешнего давления от начального равновесного значения Рi0 = Psat(Tlo) — 2/R до величины рex<plo. Среднее давление в жидкости быстро возрастает, приближаясь затем постепенно к значению Psat(Tl). Давление стабилизируется тем быстрее, чем выше Nb. При больших концентрациях квазиравновесное давление со временем постепенно понижается по мере роста пузырьков в ансамбле, что объясняется постепенным охлаждением жидкости и уменьшением величины Psat(Tl). Различие в окружающем давлении обусловливает различие скоростей роста пузырьков в ансамбле при различных концентрациях, что видно из рисунка. При любых значениях Nb скорость расширения поверхности, одинаково высокая в начальной стадии, очень быстро падает и затем медленно уменьшается, так что со временем скорость роста пузырьков перестает зависеть от их концентрации и скорости роста пузырьков в ансамбле (штрихпунктир) при резком сбросе среднего давления.
Рис.1.Изменение среднего давления в жидкой фазе (сплошная линия)
Расчеты, выполненные в рамках этой модели, показывают, что вид функции () практически не зависит от начального радиуса паровых зародышей r0. Различие в начальном размере зародышей (в интервале r0 от 5 до 50 мкм) проявляется лишь на начальной стадии процесса роста пузырьков. Столь же малое влияние на динамику роста пузырьков при одних и тех же значениях Tl0 и Nb оказывает величина сброса внешнего давления, или степень начального перегрева жидкости (3). Однако в короткой начальной стадии роста до установления квазиравновесного значения давления интенсивность расширения пузырьков тем выше, чем больше перепад внешнего давления. Вместе с тем быстрый рост пузырьков в начальной стадии приводит к более быстрому нарастанию давления внутри ячейки, что, в свою очередь, снижает интенсивность последующего расширения.
Динамика пузырьков в ансамбле и поведение ансамбля в целом определяются разностью текущих значений давления пара в пузырьке pv и среднего давления в жидкости. Давление в паровой фазе pvpv* Tv обусловлено двумя конкурирующими факторами: с одной стороны, уменьшением плотности и температуры пара из-за увеличения объема пузырька и, с другой - повышением плотности и температуры пара вследствие испарения внутрь пузырька и теплоподвода со стороны жидкости. Корректный учет этих факторов возможен только в предположении различия давления и температуры в жидкой и паровой фазах. Детальное рассмотрение кинетики фазовых переходов и взаимосвязанных процессов тепло- и массопереноса дает возможность прогнозировать эволюцию пузырькового ансамбля и рассчитывать временные зависимости величин R, wr,, ,Tl и других параметров.
Модель истечения вскипающих потоков
Основные положения модели динамически развивающегося неограниченного ансамбля положены в основу численного моделирования процессов стационарного и нестационарного истечения перегретой воды через короткие каналы в газовую среду. Двухфазный поток внутри канала рассматривается как ансамбль пузырьков в процессе его релаксации к состоянию термодинамического равновесия. Процесс релаксации осуществляется в соответствии с изложенным выше механизмом взаимосвязи между интенсивностью расширения пузырьков и локальным давлением в жидкой фазе, но в данном случае механизм установления давления в жидкой фазе протекает не только во временных, но и в пространственных координатах.
Нестационарное истечение вскипающей жидкости рассматривается в следующей постановке. В цилиндрической трубе с длиной L и постоянной площадью сечения S, закрытой с обоих концов, находится жидкость с температурой Tl0, существенно перегретая относительно внешнего давления газовой среды рg. Начальное давление жидкости plo > psat(Tlo). Предполагается, что в объеме жидкости равномерно размещены термодинамически равновесные с ней паровые зародыши малого размера с известной концентрацией Nb. В момент = 0 один из концов трубы быстро открывается и в тонкий слой жидкости, контактирующий в данный момент с газовой средой, передается внешнее давление pg « psat(Tlo), которое инициирует интенсивный рост зародышей в слое и приводит к установлению в жидкости в пределах слоя нового, более высокого значения среднего давления. Это значение , в свою очередь, определяет скорость роста паровой фазы и скорость расширения объема смеси в соседнем слое в направлении закрытого конца трубы.
При реализации модели весь объем жидкости внутри канала разбивается на п цилиндрических зон одинакового объема длиной / = L/n с фиксированными границами, причем нумерация зон начинается от открытого конца трубы. В каждой локальной зоне канала интенсивность роста пузырьков в любой момент времени определяется величиной текущего давления соседней зоны со стороны открытого конца трубы. По такой схеме осуществляется передача давления в жидкой фазе вглубь трубы, и при достаточной длине канала давление в направлении его закрытого конца асимптотически приближается к давлению насыщенного пара при температуре жидкости. Интенсивный рост паровой фазы в ансамбле пузырьков в каждой отдельной зоне ведет к увеличению общего объема двухфазной смеси и выталкиванию жидкости из канала. В любой момент времени для произвольной i зоны плотность смеси i =V/ +l(1-i), количество пузырьков в зоне Nbi = plNblS, скорость расширения объема смеси в зоне равна WRiNbi. Массовый расход смеси через сечение, разделяющее i и i-1 зоны,
линейная скорость потока через это сечение
Очевидно, при i= 1 последние выражения определяют общий расход двухфазной смеси и скорость потока на выходе из канала.
При внезапной разгерметизации трубы фронт разрежения распространяется вглубь канала со скоростью звука в однофазной жидкости при известных значениях ее температуры и давления. По мере распространение фронта уровень давления разрежения на его границе постепенно повышается с учетом указанной трансформации давления в уже пройденных зонах. В модели не вводится в рассмотрение скорость звука в двухфазной смеси, а динамика роста пузырьков в каждой i-й зоне определяется значением среднего давления в соседней i-1 зоне, вычисленным на предыдущем по времени шаге расчета. При этом в пределах каждой зоны принимается во внимание, необратимая потеря давления на трение, что позволяет учесть общие потери на трение на стенках канала.
Очевидно, что локальные значения параметров в соседних зонах различны. При движении потока в канале часть объема смеси из i зоны поступает в i-1 зону, что определяет новые значения параметров в каждой из зон. Поэтому на каждом шаге расчета значения всех определяющих микро- и макропараметров усредняются по объему зоны с учетом статистического веса доли объема смеси, поступившей из соседней зоны и доли объема смеси, остающейся в своей зоне. В рамках модели можно оценить в любой момент времени изменение массового расхода пара, жидкости и смеси в целом, распределение вдоль канала размеров пузырьков, паросодержания и плотности смеси, скорости и ускорения потока, а также плотность, температуру и давление каждой из фаз.
В случае, когда второй конец трубы не закрыт, а соединен с большой емкостью, в которой содержится под высоким давлением жидкость, существенно перегретая по отношению к внешнему давлению, модель позволяет описать переход от нестационарного истечения, вызванного внезапной разгерметизацией, к стационарному истечению вскипающей жидкости из большой емкости в атмосферу с пониженным давлением. Предполагается, что давление жидкости в емкости р0 ≥psat(Tl0). На участке перехода из емкости в трубу течение рассматривается как квазиодномерное течение однофазной жидкости в канале с прямоугольной острой кромкой, в соответствии с моделью входного участка, принятой в работе (5). Массовый расход однофазной жидкости, поступающей из емкости в трубу,
(5)
где [п] - текущее давление в последней зоне трубы (i=n), а коэффициент потери напора при внезапном сужении потока = 0,5. В режиме нестационарного истечения массовый расход жидкости на выходе из канала всегда превышает g0 и только в режиме стационарного истечения оба параметра принимают одинаковое значение.
Анализ результатов расчета
С помощью модели проведено исследование начальной (пузырьковой) стадии нестационарного истечения воды из закрытой трубы при внезапной разгерметизации одного из ее концов, а также нестационарной и стационарной ' стадий адиабатного истечения из большой емкости через короткую трубу насыщенной или недогретой воды (p0≥Psat(Tlo)), перегретой по отношению к внешнему давлению pg. Начальные значения температуры Tl0 лежали в интервале от 363 до 573 К, а значения противодавления pg в интервале от 0,01 МПа до psat(Tlо) . Истечение осуществлялось через цилиндрический канал с длиной 0,1 м и диаметром 0,01 м (L/d= 10). Во всех случаях начальный радиус паровых зародышей составлял 5 мкм, а их концентрация Nb, варьировалась в отдельных экспериментах от 105 до 107 кг-1. Для проведения расчетов канал разбивался на п =100 зон, для каждой из которой на очередном временном шаге решается система уравнений ансамбля пузырьков.
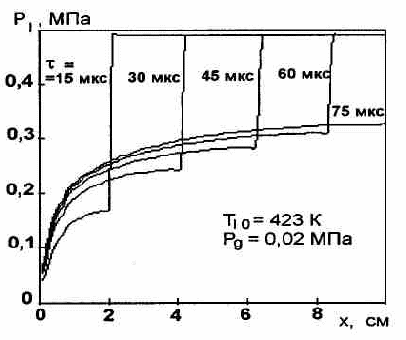
Рис.2. Распределение давления вдоль канала при распространении фронта волны разрежения в начальной стадии истечения в различные моменты времени
На рис. 2 показано распределение давления в жидкости по длине канала в различные моменты времени в начальной стадии разгерметизации закрытой трубы при прохождении волны разрежения в однофазной жидкости. Со временем давление в жидкости за фронтом волны быстро повышается, стремясь по мере приближения волны к закрытому концу трубы к значению psat(Tlо). Тем не менее, как показали исследования, на всех стадиях истечения максимальное значение давления внутри канала всегда существенно меньше давления насыщения и отличие это тем больше, чем выше температура жидкости.
Моделирование процесса нестационарного истечения вскипающей жидкости из цилиндрической трубы ограниченного объема показывает, что при любых начальных условиях истечения кривые распределения параметров по длине канала (,Pv,v,) в произвольный момент времени и временные зависимости этих параметров в произвольном сечении практически перестают зависеть от давления внешней среды pg, если противодавление pg ниже определенной для каждого режима величины рсr. Таким образом, модель предсказывает эффект запирания потока без введения специальных допущений относительно скорости распространения возмущений в двухфазной среде.
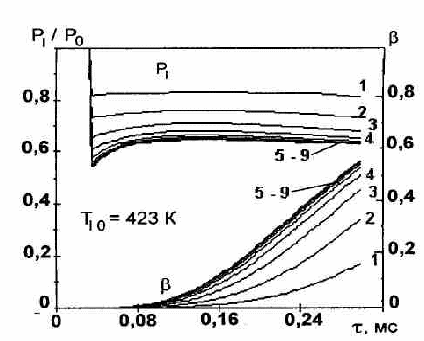
Рис. 3. Изменение со временем давления и паро-содержания в центральном сечении канала при различных значениях противодавления: 1- 0,40; 2 -0,35; 3-0,30; 4-0,25; 5-0,20; 6-0,15; 7-0,10; 8-0.05; 9-0.02Мпа
На рис.3 показано изменение со временем объемного паросодержания и величины приведенного давления /p0 в одном из сечений канала (i=50) при различных значениях противодавления. Видно, что, начиная с определенного значения рсr, дальнейшее понижение противодавления не влияет на характер этих зависимостей (кривые 5-9).
Модель корректно описывает качественно и количественно нестационарное истечение перегретой воды из канала и предсказывает основные закономерности этого процесса в широком интервале режимных параметров. Это подтверждается сравнением результатов, полученных в рамках рассматриваемой модели, с соответствующими экспериментальными и расчетными данными других авторов, например, приведенными в работе (6).
При нестационарном истечении вскипающей жидкости из канала ограниченного объема расход парожидкостной смеси резко возрастает в начальной стадии процесса и после достижения максимального значения начинает быстро понижаться. Эта закономерность наблюдается и при исследовании течения вскипающей жидкости из большой емкости в атмосферу через короткую цилиндрическую трубу.
На рис.4, для различных значений 7}0 представлены расчетные данные по изменению массового расхода вскипающей воды на выходе из канала, начиная с момента разгерметизации, при истечении из большой емкости в атмосферу с противодавлением рg= 0,1 МПа. Перегретая по отношению к внешнему давлению вода содержится в емкости в состоянии насыщения. В режиме нестационарного истечения величина расхода проходит точку максимума и затем плавно стремится к стационарному значению при данной температуре. Стационарный режим устанавливается тем быстрее, чем выше начальная температура жидкости. Эти результаты представляют определенный интерес, поскольку закономерности переходного режима от нестационарного к стационарному истечению практически не рассматривались в литературе.
Рис.4. Изменения расхода вскипающей жидкости при переходе от нестационарного к стационарному режиму течения
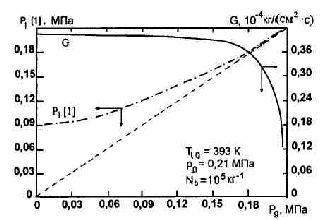
На рис.5 для различных значений Tl0 представлены кривые по длине канала давления в жидкой фазе и объемного паросодержания при истечении вскипающей воды в стационарном режиме. Кривые распределения статического давления потока носят типичный характер - постоянное или слабо понижающееся давление на большей части канала и резкое снижение давления на выходе из канала. Если при невысоких значениях входной температуры потока давление в основной части канала практически не меняется по длине, то по мере повышения Tl0 наклон кривых на основном участке заметно увеличивается. Подобная закономерность наблюдается и в экспериментах по стационарному течению вскипающих критических потоков (5,7,8). Максимальные значения статического давления в канале , существенно ниже давления торможения рo перед входом канал, и это различие увеличивается с повышением Tl0. Результаты, представленные на рис.5, показывают, что характер распределения паросодержания по длине канала качественно зависит от начальной температуры.
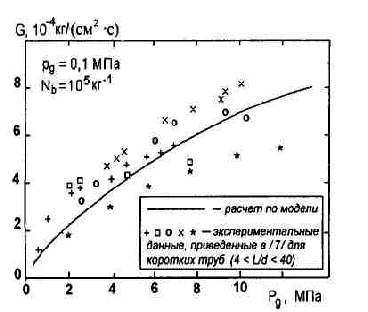
Выше отмечалось, что при описании нестационарного течения из закрытых каналов модель предсказывает появление кризиса течения, начиная с определенных для каждого режима значений противодавления рсr. При стационарных течениях вскипающих потоков модель также предсказывает эффект запирания. Критический режим течения при постоянном массовом расходе наблюдается для значений противодавления рg < рсr, причем для всех исследованных значений Tl0 критическое значение противодавления можно оценить из соотношения рсr /рo 0,8. В качестве примера на рис. 6 приведена типичная зависимость массового расхода потока от величины противодавления. На этом же рисунке показано, как меняется величина давления Рl[1] на выходе из канала (в 1-й зоне). Давление в жидкости на границе с газовой средой отличается от величины противодавления (пунктир) тем сильнее, чем ниже величины pg, т.е. чем больше режим истечения уходит в критическую область. Вне критической области с ростом рg давление в жидкости на срезе канала асимптотически приближается к соответствующему значению противодавления.
Рис.5. Распределение давления (сплошные линии) и паросодержания (пунктир) вдоль канала при стационарном истечении вскипающей жидкости при различных t/q : 1-423; 2-473; 3-503; 4-533; 5-573 К
Рис.6.Характер зависимости расхода и давления жидкости в выходном сечении канала от противодавления при стационарном истечении вскипающей жидкости
При постоянном значении противодавления величина критического расхода потока увеличивается с повышением входного давления po. Характер зависимости критических расходов от величины входного давления при истечении насыщенной или недогретой жидкости в каналах различной геометрии подробно исследован в экспериментах.
На рис.7 приведена расчетная зависимость расхода вскипающего потока от величины исходного давления перегретой воды, находящейся в насыщенном состоянии в большой емкости. На этом же рисунке представлены соответствующие экспериментальные результаты, полученные различными авторами. Эти данные взяты из работы (7), в которой анализируется и обобщается большой объем экспериментальных исследований по критическим течениям вскипающих жидкостей, Для сравнения с нашими расчетными данными выбраны результаты, касающиеся стационарного истечения через короткие цилиндрические каналы. Модель вполне удовлетворительно согласуется c опытными данными во всем исследованном интервале температур. Приведенные на рис.7 результаты подтверждают достоверность и корректность рассматриваемой модели.
Рис.7. Зависимость расхода вскипающей жидкости от давления на входе при стационарном истечении. Сравнение расчетных данных с экспериментальными.
Предполагается, что предлагаемый подход к моделированию стационарного и нестационарного истечения вскипающих жидкостей позволит получить полезную информацию и детализировать сопутствующие тепломассообменные и гидродинамические процессы.
Обозначения
d -диаметр канала; L -длина канала; / -длина зоны; р-давление; n-число расчетных зон в канале; Nb-концентрация пузырьков; r-радиальная координата; R -радиус пузырька; S -площадь сечения канала; T-температура; -скорость; w -радиальная скорость; х -координата; -объемное паросодержание; -коэффициент сопротивления; -вязкость; -плотность; -поверхностное натяжение; -время; -радиус ячейки;
Индексы: 0 -начальное значение; s -значение на межфазной границе; g-газ; l -жидкость; -пар; сr -критический; sat -насыщенный; ех -внешний.
Расчёт сопел с парогенерирующими решетками работающих на перегретой воде
В работе [9] приводится расчет сопел работающих на перегретой воде. Сообщается, что возможно создание сопел с парогенерирующими решетками которые позволяют при низких начальных давлениях ((0.5-0.8) МПа) получить коэффициент скорости до 0.85 [13].
Современные одномерные методики расчета сопел, работающих на газо- и парокапельных потоках, базируются на двух- или трехскоростных термически неравновесных моделях [14], но и они не в полной мере отражают процессы, имеющие место в реальных потоках. Как правило, делается допущение, что отсутствуют коагуляция и дробление капель, потоки считаются монодисперсными, а температура капли принимается неизменной вдоль её радиуса. Остановимся на последнем допущении и покажем, что при движении высоковлажных потоков, когда капля находится в собственном паре, оно может привести к заметному искажению достоверности результатов расчёта, особенно при наличии потоке крупнодисперсной влаги (Dк=4*10-5-8*10-5м).
Для газовых потоков, несущих испаряющиеся капли, при определении коэффициента теплоотдачи широко используется зависимость
(1)
и в большинстве случаев выполняется условие Biк0.1, что позволяет считать температуру в центре и на поверхности капли одинаковой. Однако при испарении жидкости (воды) в собственный пар коэффициент теплоотдачи на границе раздела фаз находят по формуле [15]
(2)
где [16] – коэффициент конденсации.
Если предположить, что коэффициент конденсации равен коэффициенту испарения, то для парокапельных потоков даже с малодисперсной структурой (Dк10-5м) Biк может быть значительно больше единицы. Следовательно, при расчете процессов расширения капельно-паровых потоков необходимо учитывать нестационарный характер охлаждения испаряющихся капель. Неучет этого обстоятельства, как это будет видно из результатов расчета, приведет к значительному завышению энергетических характеристик сопел, работающих на перегретой воде, по сравнению с данными, полученными из опыта.
В зависимости от степени расширения жидкости в парогенерирующей решетке можно получить за ней пузырьковую или капельно-паровую структуры. Для случая, когда степень сухости за решеткой больше граничной, при которой пузырьковая структура в парокапельную, расчет сопел, работающих на вскипающих потоках, значительно упрощается и сводится к расчету сопла, работающего на высоковлажном парокапельном потоке с учетом процессов в решетке. В более упрощенной постановке можно считать, что за решеткой поток состоит из сухого насыщенного пара и капель одного размера. Такое допущение может быть оправдано, так как результаты расчета энергетических характеристик сопла удовлетворительно согласуются с опытными данными. Ниже приводится система уравнений, позволяющая выполнить расчет сопла с парогененрирующей решеткой, работающего на перегретой воде, на основе обратной задачи с учетом нестационарного характера охлаждения капель:
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
.
Из приведенных уравнений видно, что предложенная система обеспечивает выполнение условий сохранения сплошности и энергии, так как секундный расход капель и средняя температура капли определяется из интегральных уравнений.
Для нахождения температуры на поверхности капли ТкR внутри основной программы был организован цикл, позволяющий находить корни () трансцендентного характеристического уравнения.
Предложенная физическая модель движения высоковлажного капельно-парового потока (=9*10-3-3*10-2) с учетом нестационарного процесса охлаждения капли более полно отражает процессы, имеющие место в реальных вскипающих потоках. Расчёты показывают, что в коротких соплах, работающих на парокапельных потоках с крупнодисперсной влагой, на срезе сопла средняя температура капель значительно превышает температуру пара при данном давлении, что приводит к резкому снижению располагаемого перепада энтальпии и КПД сопла (табл. 1). Выполненные расчётные исследования косвенно подтверждаются опытными результатами, в основе которых лежат массовый расход горячей воды через сопло и реакция вытекающей струи [13].
В таабл. 1 приведены результаты расчета сопла на срезе для двух случаев. В первом – коэффициент теплоотдачи от капли к пару определялся по формуле (1), во втором – по (2). Все расчеты выполнялись при следующих граничных условиях. Давление воды перед соплом р0=0.8 МПа; Т0=438 К. Давление за парогенерирующей решеткой р1=6.5*105 Па; Тк1=438К;Тп1=435 К;сп1=15м/с;ск1=10м/с;Gп1=12*10-3 кг/с; Gк1=0.4 кг/с;Dк1=8*10-5м;lс=0.150м.
На рис.1 приведены результаты расчета коэффициента скорости трех сопел длиной 0.05;0.1 и 0.15 метра при различных начальных диаметрах капель. Видно, что диаметр капель и длина сопла оказывают значительное влияние на эффективность сопел, работающих на мелкодисперсной (Dк1=8*10-6м) и крупнодисперсной влаге(Dк1=8*10-5м), дает наглядное представление о механической и термической неравновесностях потока.
Перевод сопла на мелкодисперсный поток повышает коэффициент скорости с 0.549 до 0.816 и снижает потерю кинетической энергии в 2.09 раза.
Таким образом, проведенные расчетные и экспериментальные исследования [13] сопел, работающие на перегретой воде, показывают, что при правильной организации процессов расширения коэффициент скорости сопел может быть не ниже восьмидесяти процентов.
К концепции скачка вскипания
В работе [17] рассматриваются термодинамические аспекты фазовых переходов в системе жидкость-пар применительно к процессам адиабатного расширения жидкости. Обосновывается предположение, что адиабатный скачок вскипания является термодинамически маловероятным процессом, поскольку его реализация сопряжена с убыванием энтропии в процессе неравновесных фазовых превращений.
В работах [20,21] демонстрируется рациональность концепции скачка вскипания как ударной волны разрежения для анализа процессов в неравновесных вскипающих потоках. На базе такого подхода в [23] предлагается расчетная модель, предназначенная для оценки аварийных ситуаций в ядерной энергетике когда имеет место истечение жидкости в среду с давлением, меньшим давления насыщенных паров жидкости, декомпрессия объемов с перегретой относительно внешних условий жидкостью.
Вместе с тем в работе [22] показывается физическая невозможность скачка вскипания как неравномерного процесса, не отвечающего условию возрастания энтропии. Таким образом, по одному вопросу существуют две принципиально противоположные концепции.
Поскольку рассматриваемые процессы представляют существенный практический интерес, проведен сравнительный анализ двух различных концепций для случая адиабатного истечения жидкости, сопровождающегося фазовыми переходами.
Если интерпретировать процесс перехода (рис.1) термодинамической системы из состояния 1 (перегретая жидкость) в состояние 2 (равновесная парожидкостная среда) как скачок, т.е. как геометрическую поверхность разрыва, и записать соотношение балансов массы, импульса и энергии на поверхности разрыва в виде
W11= W22=J (1)
p1+W121= p2+W222 (2)
i1+W12/2= i2+W22/2 (3)
То процесс вскипания, согласно [19], буде охарактеризован как адиабата Гюгонио. Здесь W,,i – скорость потока, плотность и удельная энтальпия вещества; р- давление;J- удельный расход через поверхность разрыва; индексы «1», «2» соответствуют параметрам среды до и после поверхности разрыва. Следствием балансовых уравнений (1)-(3) является универсальное соотношение
J2=(p2-p1)/(1-2) (4)
Где 1,2 – удельные объёмы среды. Постулируя 2>1 т.к. среда вскипает, и принимая во внимание соотношение (4), авторы работ [19-21] приходят к выводу, что неизбежно р2<р1 и процесс перехода термодинамической системы из состояния 1 в состояние 2 является ударной волной разрежения, интерпретируемой как скачок вскипания.
Анализ имеющегося экспериментального материала позволяет установить последовательность процессов, сопровождающих неравновесное течение перегретой жидкости[18,24,25]. Как показали экспериментальные исследования, при переходе жидкости из насыщенного состояния в состояние равновесной двухфазной среды реализуется метастабильное состояние, при котором давление в системе становится ниже значения на бинодали, соответствующего температуре жидкости, а вскипание ещё не происходит. Конкурирующая фаза в системе присутствует, но на уровне зародышевых образований, находящихся в динамическом процессе «зарождение-гибель», не превышая критических размеров зародышевого пузырька. Так процесс захода в метастабильную область является изотермическим, а условия устойчивости жидкой фазы относительно непрерывных изменений параметров состояния определены условием (р/)м<0, то удельный объём среды перед вскипанием должен быть больше удельного объёма недогретой или насыщенной жидкости, что и подтверждается экспериментальными данными работы [26].
На основе изложенного можно ввести понятие условного (скрытого) паросодержания среды, находящейся в метастабильном (до вскипания) состоянии и с количественной стороны охарактеризовать его отношением соответствующих удельных объёмов.
Процесс снятия перегрева, т.е. неравновесный переход из метастабильного состояния в равновесное, сопровождается вскипанием, причем, чем глубже заход системы в метастабильное состояние, тем интенсивнее вскипание. Этот процесс характеризуется повышением локального давления в системе, что соответствует реакции системы на неравновесное воздействие.
Таким образом, процесс перехода системы из состояния 1 в состояние 2 не соответствует физической интерпретации, составившей основу концепции скачка вскипания в работах [19-21], т.е. процессу представленному на рис.1, а имеет сложный двухстадийный характер (рис.2 а,б): давление в системе понижается до уровня p2, соответствующего перегреву, выдерживаемому жидкостью в данных условиях, а затем повышается от p2 до р3 при снятии перегрева, т.е. при вскипании жидкости и переходе её в состояние равновесной двухфазной среды. Естественно, что и т.е. процесс в среднем характеризуется понижением давления и увеличением удельного объёма среды, но этот усреднённый процесс – композиция двух различных процессов.
Для первой области (сечения 1,2 на рис. 2,б) p2<p1 и 2>1, что не противоречит условию (4). Именно эти условия и рассматриваются в работах [19-21] при введении концепции скачка вскипания. Но в этой области нет вскипания (нет геометрической поверхности разрыва), поэтому введение концепции скачка вскипания является преждевременным.
Для второй области (сечения 2,3 на рис.2 б), p3>p2 т.е. процесс вскипания сопряжён с ростом давления. Это не соответствует исходным данным в работах [19-21], т.е. противоречит условиям, обосновывающим концепцию скачка вскипания как ударной волны разрежения.
При p3>p2 и обязательном соблюдении универсального выражения (4) в области между сечениями 2 и 3 должно 2>3. Таким образом, процесс вскипания реализуется в области между сечениями 2 и 3, и концепции скачка вскипания в индексах выражения (4) может отвечать только одна пара условий:
P2>p1 (5) 2<1, (6)
Выражающая общеизвестное положение, что адиабатический скачок представляет собой скачок уплотнения.
Учитывая (6), можно записать
`1+(``1-`1)1>`2+(``2-`2)2, (7)
где - условное (скрытое) паросодержаниеметастабильной жидкости; 1<<2; верхние индексы «`», «``» соответствуют пару и жидкости. Так как
,
то из (7) следует
`2-`1,
т.е. если принять концепцию скачка вскипания по условиям (5) и (6), то температура равновесной парожидкостной среды, образовавшейся после вскипания, ниже температуры жидкости в метастабильном состоянии, практически равной её начальной температуре.
Рассмотрим (рис.3) процесс вскипания в ,s координатах. Расположение и конфигурация линий на рис.3 взяты с рис.72 работы [26]. Начальное состояние системы (параметры 1 и s1) перед скачком вскипания в метастабильном состоянии (вблизи спинодали) примем)соответствующим точке А.
Так как процесс снятия перегрева должен идти, согласно [25], со снижением температуры среды и 2<1, то состояние среды в конце процесса должно характеризовать параметры, соответствующие точке В, находящейся слева от точки А ниже изотермы 3 на бинодали.
Таким образом, всем возможным состояниям среды в потоке после скачка вскипания должны отвечать значения энтропии, меньшие нежели перед скачком вскипания. Отсюда следует вывод, что адиабатный скачок вскипания является термодинамически маловероятным процессом, поскольку его реализация сопряжена с убыванием энтропии в неравновесном процессе.
Процесс снятия перегрева метастабильной жидкости не является ударной волной разрежения, и его развитие не соответствует концепции скачка, а накопление конкурирующей фазы в потоке перегретой жидкости, движущейся по каналу в адиабатных условиях, должно быть непрерывным и протяженным процессом.
Рост вторичных пузырьков пара на стенке первичного пузыря в перегретой жидкости
В работе [] рассматриваются вопросы парообразования перегретой жидкости инициированного импульсами давления.
Процесс парообразования в перегретой жидкости достаточно изучен, однако воздействие импульсов давления на перегретую жидкость исследовано недостаточно. В связи с этим представляет интерес рассмотрение вопросов взаимодействия перегретой жидкости с ударной волной, образование и рост паровых пузырьков в перегретой жидкости, увеличение межфазной границы пар-вода.
В экспериментах производилась скоростная съёмка (104 к/с) перегретой капли воды, помещённой в среду расплавленного парафина. Возникновение зародыша пузыря в капле инициировалось электрическим разрядом. Снимки показали, что уже через 10-4 с после прохождения инициирующей ударной волны образуется зародыш пузырька радиусом R 0,25 мм, и он начинает расти. В дальнейшем в процессе роста зародыша на его межфазной поверхности пар - жидкость образуются конусообразные углубления в жидкости, которые очень быстро преобразуются во вторичные пузырьки пара, окружающие первичный пузырь. Вблизи поверхности вторичных пузырьков образуются новые пузырьки и т.д. Процесс носит взрывной характер и уже через время порядка 10-3 с весь объем перегретой капли оказывается заполненным паровыми пузырьками, которые продолжают расти. Заканчивается этот процесс паровым взрывом с возникновением ударной волны.
Образование вторичных пузырьков может происходить по следующей схеме:
• рост радиуса первичного пузыря R, падение давления в нем до внешнего ро, рост толщины теплового пограничного слоя ;
• уменьшение толщины на некоторых участках вследствие неравномерного роста поверхности парового пузыря, что вызывает некоторое повышение температуры поверхности этих участков над остальной поверхностью и появление термокапиллярного движения жидкости на границах этих участков, направленного на дальнейшее уменьшение толщины ;
• происходит лавинообразное уменьшение толщины до минимальной вследствие преимущественного роста поверхности пузыря за счет более нагретых участков, т.к. в них поверхностное натяжение меньше;
• увеличивается испарение вследствие уменьшения , что ведет к увеличению давления отдачи и образованию канала, направленного в глубь жидкости;
• устье канала замыкается действием сил поверхностного натяжения и в образовавшемся вторичном пузырьке формируется свой пограничный тепловой слой.
Будем считать, что толщина теплового пограничного слоя в лавинообразном процессе уменьшается до min такого, при котором избыточное давление пара над перегретой жидкостью P (T ) уравновешивается средним давлением отдачи пара РОТд. Давление отдачи можно вычислить из закона сохранения импульса
где m,кг/см2 - поток массы пара от испаряющей поверхности жидкости; W - приращение нормальной скорости пара.
Поток массы и приращение скорости можно определить по формулам
где - теплоемкость жидкости; р - плотность пара, min - наименьшая толщина теплового, пограничного слоя в зоне роста вторичного пузыря. Отсюда получаем
где величину АР можно определить по формуле Клапейрона - Клаузиуса в виде
где v", v1 - удельные объемы пара и жидкости соответственно. Например, для .
T =10 К min =1,6-10-8м.
В области, где —> mjn, величина в лавинообразном процессе является функцией времени и площади этой области = (,S). Точка = mjn является, очевидно, точкой минимума . Условие минимума
Входящие в выражение (5) производные можно вычислить. Из соотношения = Va , где а - температуропроводность жидкости, получим
Величину dS/d можно определить, считая, что все приращения поверхности первичного пузыря в лавинообразном процессе происходят за счет области, где —» min, тогда
Вблизи точки минимума должно выполниться соотношение S = Sm min ~ const, поэтому
где Sm - величина площади области, где 8 = 8min .
Подставляя (6), (7), (8) и используя известную зависимость радиуса пузыря от времени (4), получим соотношение для области минимума
Из фотографий было видно, что размер этой области мал (меньше 0,01 мм), поэтому определить форму и размер ее в наших опытах не представлялось возможным.
Будем считать эту область сферой радиуса Rm и площадью сечения Sm=Rm 2. Предположим также, что такая область только одна. Используя (9),получим
Для T=10К, например, Rm 4,2-10-6 м. При достижении тепловым пограничным слоем в жидкости толщины mjn в круге радиусом Rm давление отдачи пара компенсируется только искривлением поверхности, т.к. давление внутри пузыря мало отличается от внешнего, силой инерции жидкости также можно пренебречь. Поэтому для того, чтобы давление РОТд смогло продавить стенку первичного пузыря в области Sm и образовать выпуклость в стенке, из которой образуется вторичный пузырек вблизи стенки первичного пузыря, необходимо, очевидно, выполнение условия
где - коэффициент поверхностного натяжения в области Sm.
Подставляя (3), (7) в (8),получим величину перегрева жидкости, при котором уже возможно образование вторичных пузырьков
Например, в наших опытах использовалась вода, и парообразование в перегретой капле с характерным звуком удара и образованием вторичных пузырьков начиналось при воздействии разряда при перегреве T > 10 К. При Т < 10 К процесс парообразования происходил без образования вторичных пузырьков и без такого звука.
Вычисляя по формуле (12), получим T > 9,2 К. Видно достаточное для такой простой схемы расчета совпадение опытных и рассчитанных величин перегрева.
Таким образом, экспериментально установлено, что при росте парового пузырька в достаточно перегретой жидкости непосредственно вблизи поверхности растущего пузырька в жидкости возникают и растут множество вторичных пузырьков. Лавинообразный рост суммарной поверхности испарения приводит к росту скорости парообразования в перегретых участках жидкости, окружающей расплав, что может составить заметную долю в импульсе давления при паровых взрывах. Если известны параметры расплава и жидкости (температуры, давление, масса расплава или размеры фрагментов расплава), процесс лавинообразного парообразования может быть рассчитан по форму лам, приведенным в настоящей работе. Кроме того, полученные' физические представления могут быть полезны для прогнозирования и расчета сложных процессов, протекающих при паровом взрыве.
Литература
1.Моделирование стационарного и нестационарного истечения адиабатно вскипающей жидкости из коротких каналов. Институт технической теплофизики НАН Украины, г.Киев
2. Долинский А.А., Иваницкий Г.К. Теоретическое обоснование принципа дискретно-импульсного ввода энергии. I. Модель динамики одиночного парового пузырька //Пром. теплотехника. 1995. Т.17, N5. С.3-28.
3. Долинский А.А., Иваницкий Г.К. Теоретическое обоснование принципа дискретно-импульсного ввода энергии. П. Исследование поведения ансамбля паровых пузырьков //Пром. теплотехника. 1996. T.18,N1. С.3-20.
4. Нигматулин Р.И. Основы механики гетерогенных сред. М: Наука, 1978. 336 с.
5. Нигматулин Б.И., Сопленков К.И., Блинков В.Н. Критическое стационарное истечение вскипающей воды через трубы и сопла //ТВТ. 1987. T.25,N4. C.726-735.
6. Нигматулин Б.И., Сопленков К.И. Исследование нестационарного истечения вскипающей жидкости из каналов в термодинамически неравновесном приближении //ТВТ. 1980. Т.18, N1.C.118-131.
7. Фисенко В.В. Критические двухфазные потоки. М.: Атомиздат, 1978. 159 с.
8. Тихоненко Л.К., Кеворков Л.Р., Лутовинов С.З. Исследование локальных параметров критического потока горячей воды в прямых трубах с острой входной кромкой //Теплоэнергетика. 1978. N2. С.41-44.
9.Барилович В.А. Расчет сопел с парогенерирующими решетками работающих на перегретой воде// Теплоэнергетика.
10. Барилович В.А. Смирнов Ю.А. Стариков В.И. О тепловой эффективности геотермальных электростанций // Теплоэнергетика. -1985.-№11.-с.54-56.
11. Барилович В.А. Петрущенков В.А. Некоторые результаты экспериментального исследования гидропаровой турбины// Энергетика… (Изв. высш. уч. заведений).-1981.-№5.-с.47-52.
12. Вскипающие адиабатные потоки/ В.А. Зысин и др.-М.:Атомиздат,1976.-152с.
13. Пути повышения эффективности сопел работающих на вскипающих потоках/ В.А. Барилович и др.//Энергетика…(Изв. высш. уч. заведений).-1985.-№5.-с.56-60.
14.Нигматуллин Р.И. Основы механики гетерогенных сред.-М.:Наука,1978.-336с.
15.Справочник по теплообменникам: в 2 т. Т.1./Пер. с англ., Под ред. Петухова Б.С., В.К. Шикова.- М.:Энергоатомиздат,1987.-560с.
16.Галин Н.М. Кириллов П.Л. Тепломассобмен (в ядерной энергетике).-М.:Энергоатомиздат,1987.-375с.
18.И.Ф. Муравьев, Б.М. Павлов, В.Г. Тонконог. К концепции скачка вскипания// Изв. Вузов. Авиационная техника 1995 №1.
19. Тонконог В.Г. Муравьёв И.Ф. Павлов Б.М. Метастабильные состояния, реализуемые в процессах адиабатного расширения жидкостей // Тез. докл. Восьмой всесоюз. конф. «Двухфазные потоки в энергетических машинах и аппаратах»/ Л., 1990. т3. с.338.
20. Лабунцов Д.А. Авдеев А.А. Механизм запирания потока при ударном вскипании жидкости// Теплофизика высоких температур. 1981 №3 т.19 с.552-558.
21. Лабунцов Д.А. Авдеев А.А. Механизм запирания потока при ударном вскипании жидкости// Теплофизика высоких температур. 1982 №1 т.20 с.88-95.
22. Лабунцов Д.А. Авдеев А.А. Механизм нестационарного истечения вскипающей жидкости// Теплофизика высоких температур. 1982 №2 т.20 с.288-295.
23.Вайсман М.Д. Термодинамика парожидкостных потоков. Л.:Энергия, 1987. 371с.
24. Хлесткин Д.А. Определение расходов метастабильной жидкости// Теплоэнергетика №1. 1978. с.78-81.
25.Гуров В.И. Шенстаков К.Н. О механизме предельно-срывного по расходу течения кавитирующей жидкости в лопастном насосе // Тр.ЦИАМ. 1976 №895. с.1-8.
26.Скрипов В.П. Метастабильная жидкость. М.:Наука,1972. 842с.
27. Н.Н. Авакимян, Н.И. Васильев, В.В. Гугучкин, А.С. Трофимов. Рост вторичных пузырьков пара на стенке первичного пузыря в перегретой жидкости.
28. Bankoff S.C. Vapor explosions: a critical review//'Proc. of VI H. conf. Toronto, Canada, 1978. Vol. 6, p. 355-360.
29. Ochiai M., Bankoff S.C. Third Spec.Mtg on SFL. Tokyo, 1976. Vol. 1, p. 129-152.
30. Зверев, В.К. Сироткин. Генерирование волн в неравновесной многокомпонентной среде. Препринт ИАЭ-5735/1. М., 1994.
31. Кузнецов Ю.Н. Теплообмен в проблеме безопасности ядерных реакторов. М.: Энергоиздат, 1989. 296с.
32. Cicarelly, Frost D.L. Fragmentation mechanism based on single drop experiments using flash x-Ray photography//!, of Heat Transfer 1981, Vol. 103, p. 61-64.
33. Фрост Д., Стуртевант Б. Влияние давления окружающей среды на устойчивость взрывного вскипания предельно перегретой жидкости //Теплопередача, 1986, ?2, 198.
34. S. Lesin, A. Baron, I. Zibberman, H. Branover and J. C. Merchuk. Direct contact boiling studies applicable for liguid metall MHD systems // Pros, of the 2nd Int. Conf. on Multiphase Flow'95- Kyoto, April 3-7, 1995, p. РС2-1ч-РС2-6.

Нравится материал? Поддержи автора!
Ещё документы из категории химия:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ