Определение массы полимера криоскопическим способом
















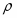
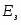
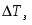
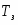
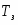
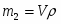
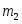
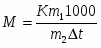
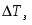
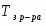
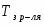
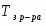
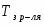
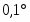
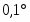
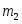
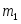
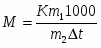
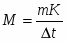
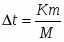
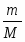
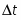
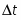
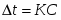
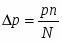
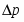
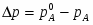 План
План
Обоснование выбранной темы.
Сущность криоскопического метода определения молекулярной массы вещества.
Закон Рауля применительно к разбавленным растворам.
Диаграмма состояния воды.
Графическое изображение закона Рауля для разбавленных растворов.
Понижение температуры замерзания растворов.
Связь понижения температуры замерзания растворов с мольной концентрацией.
Криоскопическая постоянная и её физический смысл.
Формула для расчёта молекулярной массы криоскопическим методом.
Экспериментальная часть.
Мы выбрали тему – «Определение молекулярной массы вещества криоскопическим методом». Изучая высокомолекулярные соединения, мы отметили, что их важной характеристикой является молекулярная масса, от которой зависят свойства. Так как в химии формула полимера неопределённая, то есть нет точного количества атомов элементов, а пишется только структурное звено и степень полимеризации, то по формуле молекулярную массу полимера рассчитать нельзя, её определяют экспериментально. Для этого существует много способов: по осмотическому давлению, по давлению пара над раствором высокомолекулярного соединения согласно закону Рауля; эбуллиоскопическим методом (через температуру кипения раствора и чистого растворителя); криоскопическим методом (через температуру замерзания раствора и растворителя). Учитывая, что в наших лабораторных условиях мы не можем получить очень низкую температуру, мы изучили один из вышеуказанных методов, а именно: криоскопический метод для определения молекулярной массы вещества на примере мономера. В качестве растворённого вещества мы взяли нафталин, а в качестве растворителя – бензол.
Сущность криоскопического метода.
Криоскопическим называется метод определения молекулярной массы по понижению точки замерзания растворителя. Для исследования этого метода нам необходимо вспомнить закон Рауля применительно к разбавленным растворам. Мы знаем, что давление насыщенного пара каждой жидкости есть величина постоянная для данной температуры. При растворении в жидкости какого-либо твёрдого вещества давление пара жидкости понижается. Таким образом, давление пара раствора всегда ниже давления пара чистого растворителя при той же температуре. Разность между числовыми значениями давления пара чистого растворителя и давления пара раствора называется обычно понижением давления пара растворителя над раствором. Это можно выразить формулой:
В 1887 году французский физик Рауль на основании многочисленных опытов с растворами различных твёрдых веществ и нелетучих жидкостей установил следующий закон: в разбавленных растворах неэлектролитов при постоянной температуре понижение давления пара пропорционально количеству вещества, растворённого в данном количестве растворителя. Объяснение этому закону даёт молекулярно-кинетическая теория. Давление находящегося над жидкостью насыщенного пара зависит от числа молекул, испаряющихся с поверхности жидкости в единицу времени. Но в растворе часть его свободной поверхности занята молекулами нелетучего растворённого вещества. Поэтому число молекул, покидающих поверхность раствора в единицу времени, становится меньше, чем в случае чистого растворителя при той же температуре, и давление пара понижается. Например, давление пара раствора, в котором число молекул растворённого вещества составляет 1/20 всего числа молекул, на 1/20 меньше давления пара чистого растворителя.
Зависимость между понижением давления пара и количеством растворённого вещества может быть выражена в математической форме. Обозначим давление чистого растворителя через p, понижение давления пара через , число молей растворённого вещества через n и число молей растворителя через N. Тогда закон Рауля для разбавленных растворов выразится уравнением:
Измерением понижение давления пара раствора можно пользоваться для определения молекулярной массы растворённых веществ. Однако на практике обычно применяется другой, более удобный метод, основанный на измерении понижения температуры замерзания раствора.
Все чистые вещества характеризуются строго определённой температурой замерзания. Так, чистая вода при нормальном атмосферном давлении замерзает при 0º С; бензол при +5,5º С. Эти температуры сохраняются неизменными до тех пор, пока вся жидкость не замёрзнет или не превратится в пар.
Иначе обстоит дело с растворами. Присутствие растворённого вещества понижает точку (или температуру) замерзания растворителя, и тем сильнее, чем концентрированнее раствор. Поэтому растворы замерзают при более низких температурах, чем чистые растворители. Нетрудно доказать, что это является прямым следствием понижения давления пара растворов. Более низкая температура замерзания раствора, по сравнению с чистым растворителем, объясняется тем, что температура замерзания есть та температура, при которой одновременно могут существовать твёрдая и жидкая фазы данного вещества.
p
A C
760
мм. рт. ст.
вода лёд
O
4,6
пар
B
100 0,01 t, ºC
Диаграмма состояния воды.
Показанная выше зависимость между давлением водяного пара и температурой, а также условия одновременного существования воды в различных фазах могут быть наглядно представлены при помощи диаграммы состояния воды. На этой диаграмме линия ОА представляет кривую давления паров воды, а линия ОВ – кривую давления паров льда. Точки кривой ОА показывают, при каких температурах и давлениях могут одновременно существовать в равновесии вода и пар; точки кривой ОВ определяют условия равновесия между льдом и паром. Обе кривые пересекаются в точке О, указывающей температуру и давление, при которых могут находиться в равновесии все три фазы.
Поэтому точка О называется тройной точкой; ей отвечает давление 4,6 мм.рт.ст. и температура +0,01º С. Кривая ОС показывает влияние давления на точку плавления льда. Каждой её точке соответствует определённое давление и определённая температура, при которых лёд и вода находятся в равновесии. Однако для этого необходимо, чтобы давление пара твёрдой и жидкой фаз было одинаковым, иначе пар будет переходить от одной фазы к другой до полного исчезновения той из них, над которой давление пара больше. Одновременное существование льда и раствора будет возможно только при температуре ниже 0º С, и именно при такой, при которой давление их паров станет одинаковым. Другими словами, раствор будет замерзать при более низкой температуре, чем чистый растворитель. Все эти соотношения становятся особенно ясными, если изобразить их графически, начертив кривые изменения давления паров с температурой.
a p
b мм. рт. ст.
вода
A
раствор
B C
T1 T t, ºC
На графике линия Аа изображает кривую давления пара чистой воды, а линия Bb – кривую давления пара над раствором. Так как при любой температуре давление пара раствора меньше давления пара чистой воды, то линия Bb лежит ниже линии Аа. Линия АС изображает кривую давления пара льда. Мы уже говорили, что при температуре замерзания давления паров твёрдой и жидкой фаз растворителя или твёрдого растворителя и раствора должно быть одинаковым. Этому условию отвечают точки А и В пересечения кривых Аа и Bb с кривой АС. Температуры замерзания воды и раствора определяются как проекции точек А и В на ось абсцисс. В этом случае, как видно из графика, температуры Т и Т1, расположены в обратном порядке, то есть температура замерзания раствора ниже температуры замерзания воды.
При замерзании разбавленных растворов вначале выделяется в твёрдом виде чистый растворитель, например в случае водного раствора – чистый лёд. Так как ко мере выделения льда концентрация раствора увеличивается, то температура замерзания не остаётся постоянной, а постепенно понижается Однако выделение льда и понижение температуры замерзания происходят лишь до тех пор, пока концентрация раствора не достигнет некоторой определённой для данного вещества величины, при которой весь раствор застывает в сплошную массу. Такая масса получила название эвтектики. Температура, при которой происходит её образование, называется эвтектической температурой, а соответствующая концентрация раствора – эвтектической концентрацией.
С количественной стороны явление замерзания раствора было изучено Раулем, который экспериментальным путем установил следующие положения, известные под названием законов Рауля: 1) понижение точки замерзания пропорционально количеству вещества, растворённого в данном количестве растворителя; 2) эквимолекулярные количества различных веществ, будучи растворены в одном и том же количестве данного растворителя, понижают его точку замерзания на одно и то же число градусов. Понижение температуры замерзания, соответствующее растворению 1 моля вещества в 1000 граммах растворителя, есть величина постоянная для данного растворителя. Она называется криоскопической (от греч. «криос» - холод, «скопео» - смотрю) константой растворителя.
Математически законы Рауля могут быть выражены следующим уравнением:, где - понижение точки замерзания растворителя; С – число молей растворённого вещества, приходящееся на 1000 граммов растворителя; К – коэффициент пропорциональности, равный соответственно криоскопической константе растворителя (при С=1 величина =К).
Так как число молей вещества равно его массе в граммах (m), делённой на молекулярный вес (M), то, заменив в предыдущем уравнении С на , получим: . Из этого уравнения выражаем молекулярную массу: . Но существует формула для любого количества растворителя: , где - масса растворённого вещества; - масса растворителя.
Экспериментальная часть
В экспериментальной части работы ставилась задача опытным путём определить понижение температуры замерзания приготовленного раствора и вычислить молекулярный вес растворённого вещества (неэлектролита).
При этом использовались следующие приборы:
Широкая пробирка с боковым отростком и кожухом.
Термометр с ценой деления или термометр Бекмана.
Лупа.
Бюкс
Охладительная смесь (лёд + NaCl).
Чистый бензол (для криоскопии).
Испытуемое вещество, растворимое в бензоле.
Мешалка.
Широкий стакан для охладительной смеси.
Ход работы
Для определения температуры затвердевания растворителя и раствора пользуются специальным прибором, состоящим из широкой пробирки с боковым отростком, вставленной в более широкую пробирку – кожух. Во внутреннюю пробирку на пробке устанавливают термометр Бекмана или термометр с ценой деления . Пробирку с кожухом помещают в широкий стакан, заполненный охладительной смесью. В пробирке для перемешивания жидкости имеется стеклянная или металлическая мешалка.
В сухую пробирку отбирают пипеткой 11,38 мл. чистого бензола и погружают в него термометр таким образом, чтобы резервуар со ртутью был полностью погружён в жидкость, но не касался дна и стенок. Боковой отросток закрывают пробкой. Вставляют пробирку в кожух и помещают в охладительную смесь. Осторожно помешивая жидкость, следят за показаниями термометра. Температура сначала понизится немного ниже точки затвердевания (явление переохлаждения), а затем с появлением кристаллов несколько повысится и установится на некотором постоянном уровне. Эта температура и является температурой затвердевания чистого растворителя. Повторяют такое измерение 2-3 раза. Для этого пробирку вынимают, нагревают рукой до исчезновения кристаллов, снова помещают в охладительную смесь и определяют . Отсчёт температуры производят с помощью лупы. В бюксе на аналитических весах отвешивают навеску исследуемого вещества, то есть нафталина, массой 0,124 г. Открыв боковой отросток пробирки, вводят навеску, закрывают пробкой и, осторожно помешивая, добиваются полного растворения вещества в бензоле.
Аналогично описанному определению находят температуру затвердевания полученного раствора , повторяя измерение так же 2-3 раза.
По разности и вычисляют .
Расчёт молекулярного веса растворённого вещества производят по формуле , предварительно найдя К для бензола по таблице. Массу растворителя (бензола) находят по формуле где V – объём растворителя, а ρ – плотность растворителя (табличная величина).
Все опытные табличные данные записывают в таблицу.
Объём р.-ля, мл
р.-ля (бензол), º
Масса пустого бюкса, г
Масса бюкса с в.-вом, г
Масса навески в.ва (нафталина), г
р.-ра,
º
, º
, º
, г/мл
M, г/моль
11,38
4,56
1,01
1,134
0,124
4,064
0,496
5,12
0,879
127,5
Проведя вычисления, мы получили, что масса нафталина M=127,5 г/моль. У нафталина молекулярная масса равна 128 г/моль, следовательно, процент ошибки очень невелик.
Вывод.
Во-первых, проводя опыт, мы познакомились с новым для нас прибором – термометром Бекмана. Во-вторых, в ходе работы мы познакомились с одним из способов определения молекулярной массы.
Список использованной литературы.
Н.Л. Глинка «Общая химия», издательство «Химия», Москва, 1965.
Н.К. Воробьёв, В.А. Гольцшмидт, М.Х. Карапетьянц «Практикум по физической химии», Государственное научно-техническое издательство химической литературы, Москва, 1950
А.И. Бродский «Физическая химия», Т.2, Росхимиздат, Ленинград, 1948

Нравится материал? Поддержи автора!
Ещё документы из категории химия:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ