Оптимизация химического состава сплава






МИНИСТЕРСТВО ВЫСШЕГО И СРЕДНЕГО СПЕЦИАЛЬНОГО ОБРАЗОВАНИЯ РФ
УРАЛЬСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Нижнетагильский институт
Кафедра металлургической технологии
Расчетно-пояснительная записка по дисциплинам
«Математическое моделирование и оптимизация металлургических
процессов»
«Вычислительная техника в инженерных расчетах»
Оптимизация химического состава сплава
Студент: Бородин А.Н.
Группа: 321 – ОМД
Преподаватель: Грузман В.М.
Преподаватель: Баранов Ю.М.
1998г.
Содержание
-
Введение
4
Глава 1
Верхний, нижний и основной уровень.
Расчет интервала варьирования
5
Глава 2
Расчет уравнений
7
Расчет уравнения для C, Si и σ текучести
7
Расчет уравнения для С, Si, относительного удлинения
11
Расчет уравнения для С, Si, предела прочности
13
Глава 3
Проверка уравнений
17
Глава 4
Оптимизация состава сплава
18
Целью нашей работы является нахождение оптимального состава стали М74 для получения наилучших физических свойств сплава: предела текучести, предела прочности, абсолютного удлинения. В данной работе использован метод линейного программирования и дальнейшая оптимизация по двухфакторной модели, что позволило получить одновременно решение графическим методом и на ЭВМ.
В ходе работы был определен наилучший состав стали по заданным требованиям:
для получения минимального предела текучести содержание углерода и кремния должно быть следующим: C=0,7%; Si=0,4%;
для получения максимального предела прочности: C=0,8%; Si=0,25%;
для получения максимального абсолютного удлинения: C=0,7%; Si=0,4%.
ВВЕДЕНИЕ
Математическая модель является эффективным современным средством управления производством. В современных условиях быстроизменяющейся обстановке во всех сферах металлургического производства, от исходных материалов до готовой продукции, когда необходимо быстро и с минимальной ошибкой принимать ответственные решения, необходимо знание основ математического моделирования, уметь не только пользоваться готовыми моделями, но и принимать участие в их создании.
Линейное программирование - один из самых распространенных методов решения оптимизационных задач на практике. Он является частью математического программирования вообще, направленного на решение задач о распределении дефицитных ресурсов с учетом технологических, экономических и других ограничений, накладываемых условиями функционирования реального моделируемого объекта. Для линейного программирования используют линейные математические зависимости. Рождение метода линейного программирования связано с именами фон Неймана, Хичкока, Стиглера, которые использования положения теории линейных неравенств и выпуклых множеств, сформулированные в прошлом веке, для оказания помощи руководителям в принятии оптимальных решений. Основная задача линейного программирования была сформулирована в 1947 году Георгом Данцигом из управления ВВС США, который высказал гипотезу, что к анализу взаимосвязей между различными сторонами деятельности крупного предприятия можно подходить с позиций линейного программирования, и что оптимизация программы может быть достигнута максимизацией (минимизацией) линейной целевой функции.
В металлургической технологии наибольшее распространение получила задача составления технологических смесей, а конкретно, задача оптимизации химического состава сплавов.
Для того, чтобы исследовать метод «Оптимизации химического состава сплава», я воспользовался данными из прокатного цеха НТМК, которые отражают влияние содержания углерода и кремния в стали М74 на ее физические свойства: предел текучести, предел прочности и абсолютное удлинение. Данные взяты в ЦЛК (см. приложение 2).
ГЛАВА 1
ОПРЕДЕЛЕНИЕ ВЕРХНЕГО, НИЖНЕГО И ОСНОВНОГО УРОВНЯ. РАСЧЕТ ИНТЕРВАЛА ВАРЬИРОВАНИЯ
По данным выборки назначим верхний и нижний уровень варьирования факторов и рассчитаем интервал варьирования и средний (основной, нулевой) уровень.
Для этого построим таблицу, отражающую частоту «попадания» каждого числа:
Таблица 1
Подсчет частот
-
Х1
К1
Х2
К2
0,71
7
0,25
2
0,72
26
0,26
5
0,73
50
0,27
0
0,74
49
0,28
6
0,75
79
0,29
11
0,76
35
0,30
21
0,77
53
0,31
38
0,78
48
0,32
88
0,79
36
0,33
66
0,8
9
0,34
44
0,81
4
0,35
28
0,82
4
0,36
42
0,37
29
0,38
7
0,39
13
Итого
400
400
Таблица 2
Нижний, верхний, основной уровень и интервал варьирования
-
Факторы
Х1
Х2
Нижний уровень
0,71 –0,74
0,25 – 0,29
Верхний уровень
0,80 – 0,83
0,37 – 0,41
Основной уровень
0,77
0,32
Интервал варьирования
0,04
0,05
Для нахождения среднего уровня выполняем следующие расчеты:
Найдем средние значения каждого интервала и основной уровень.
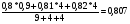
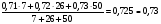
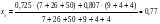 основной уровень
основной уровень
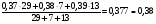
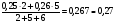
основной уровень х2= 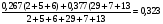 0
0
ГЛАВА 2
РАСЧЕТ УРАВНЕНИЙ
Необходимо рассчитать три уравнения:
уравнение для C, Si и σ текучести,
уравнение для C, Si и относительного удлинения,
уравнение для C, Si и σ прочности.
2.1. Расчет уравнения для C, Si и σ текучести
Для того, чтобы оценить влияние факторов, часто имеющих разную размерность, производится кодирование – факторы делаем безразмерными, кроме этого кодирование обеспечивает легкость обработки данных.
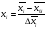 , где хi - кодированная переменная.
, где хi - кодированная переменная.
2.1.1.Составление матрицы планирования
Таблица 3
Матрица планирования
-
N
X1
Х2
y1
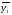
x1x2
1
1
1
667(40)
667
1
2
1
-1
589(20)
608,5
-1
628(357)
3
-1
1
647(45)
603,5
-1
589(12)
589(191)
589(310)
4
-1
-1
598(19)
586,4
1
598(134)
540(165)
598(253)
598(372)
2.1.2. Определение коэффициентов регрессии
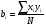 ,
,
где N - число опытов по матрице планирования.
b0 =(667+603,5+586,4+608,5)/4=616,35
b1 =(667+608,5-603,5-586,4)/4=21,4
b2 =(667-608,5+603,5-586,4)/4=18,9
b3 =(667-608,5-603,5+586,4)/4=10,35
2.1.3. Проверка значимости коэффициентов при факторах
Дисперсия воспроизводимости служит для оценки ошибки опыта, для этого необходимо найти опыты в центре плана, для чего составим табл.4.
Таблица 4
Опыты в центре плана.
-
N
X1
x2
y1
3
0,77
0,32
589
96
598
118
589
138
598
215
598
594.4
237
589
257
598
334
598
356
589
376
598
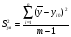 ,
,
где m – число опытов
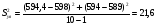
Проверка значимости коэффициентов регрессии.
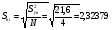 ;
;
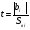 ;
;
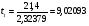 ;
;
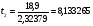 ;
;
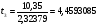
tтабл. = 2,26; т.е. все коэффициенты значимы.
Получили уравнение 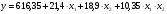
2.1.4. Проверка адекватности математической модели
Проверяем адекватность математической модели по критерию Фишера. Для получения адекватности необходимо, чтобы разброс в точке и разброс в регрессии был сопоставим. 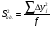 ,
,
где f =N-(k+1)=4-(3+1)=0
Y1=616,35+21,4+18,9+10,35=667
Y2=616,35+21,4-18,9-10,35=608,5
Y3=616,35-21,4+18,9-10,35=603,5
Y4=616,35-21,4-18,9+10,35=586,5
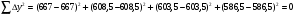
Критерий Фишера
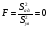
Математическая модель адекватна.
2.1.5. Переход от кодированных переменных к натуральным
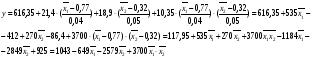
2.2. Расчет уравнения для С, Si, относительного удлинения
2.2.1. Составление матрицы планирования
Таблица 5
Матрица планирования
-
N
x1
x2
x1x2
y2
1
1
1
1
6,7(40)
6,7
2
1
-1
-1
5(20)
5,5
6(357)
3
-1
1
-1
7,3(45)
9,85
10,7(12)
10,7(191)
10,7(310)
4
-1
-1
1
6(19)
6,2
6(134)
7(165)
6(253)
6(372)
2.2.2. Расчет дисперсии воспроизводимости
Таблица 6
Опыты в центре плана
-
N
x1
x2
y2
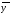
3
0,77
0,32
7,3
6,1
96
5,3
118
7,3
138
5,3
215
5,3
237
7,3
257
5,3
334
5,3
356
7,3
376
5,3
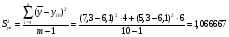
2.2.3. Определение коэффициентов регрессии
b0 =(6,7+5,5+9,85+6,2)/4=7,0625
b1 =(6,7+5,5-9,85-6,2)/4=-0,9625
b2 =(6,7-5,5+9,85-6,2)/4=1,2125
b3 =(6,7-5,5-9,85+6,2)/4=-0,6125
2.2.4.Проверка значимости коэффициентов регрессии
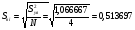 ;
;
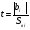 ;
;
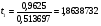 ;
;
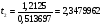 ;
;
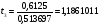
tтабл. = 2,26; t3< tтабл. , t2< tтабл., т.е. эти коэффициенты незначимы.
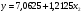
2.2.5. Проверка адекватности математической модели
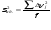
Y1=7,0625+1,2125=8,275
Y2=7,0625-1,2125=5,85
Y3=7,0625+1,2125=8,275
Y4=7,0625-1,2125=5,85
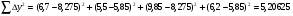
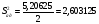
Критерий Фишера: 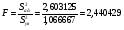 ; Fрасч.
; Fрасч.
Математическая модель адекватна.
2.2.5. Переход от кодированных переменных к натуральным
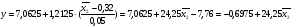
2.3. Расчет уравнения для С, Si, предела прочности
2.3.1. Составление матрицы планирования
Таблица 7
Матрица планирования
-
N
x1
x2
x1x2
Y3
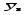
1
1
1
1
1079
1079
2
1
-1
-1
1030
1044,5
1059
3
-1
1
-1
1028
1024,5
1010
1040
1020
4
-1
-1
1
1020
1028
1030
1010
1040
1040
3.2.Вычисление дисперсии воспроизводимости
Таблица 8
Опыты в центре плана
N
X1
x2
y2
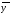
3
0,77
0,32
1010
1006,5
96
1010
118
1030
138
1001
215
991
237
1001
257
991
334
1010
356
1001
376
1020
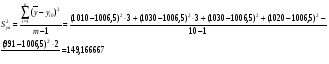
2.3.3. Определение коэффициентов регрессии
b0 =(1079+1044,5+1024,6+1028)/4=1044
b1 =(1079+1044,5-1024,6-1028)/4=17,75
b2 =(1079-1044,5+1024,6-1028)/4=7,75
b3 =(1079-1044,5-1024,6+1028)/4=9,5
2.3.4. Проверка значимости коэффициентов регрессии
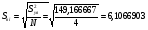 ;
;
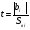 ;
;
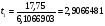 ;
;
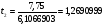 ;
;
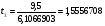
tтабл. = 2,26; t3< tтабл. , t2< tтабл., т.е. эти коэффициенты незначимы.
2.3.5. Проверка адекватности математической модели
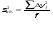
Y1=1044+17,75=1061,75
Y2=1044+17,75=1061,75
Y3=1044-17,75=1026,25
Y4=1044-17,75=1026,25
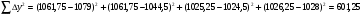
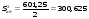
Критерий Фишера: 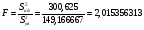 ; Fрасч.
; Fрасч.
Математическая модель адекватна.
2.3.6. Переход от кодированных переменных к натуральным
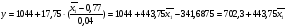
ГЛАВА 3
ПРОВЕРКА УРАВНЕНИЙ
Проверим составленные уравнения, отражающие влияние содержания углерода и кремния в стали на ее физические свойства.
Таблица 9
Проверка уравнений
N опыта
295
392
149
x1=
0,75
0,73
0,79
x2=
0,39
0,29
0,33
yпр1.=
687
589
589
yрасч1.=
632,69
604,61
643,81
yпр.2=
10,7
6
6
yрасч.2=
8,76
6,335
7,305
yпр.3=
1059
1030
1001
yрасч.3=
1035,1125
1026,2375
1052,8625
ГЛАВА 4
ОПТИМИЗАЦИЯ СОСТАВА СПЛАВА
Необходимо оптимизировать химический состав сплава по C и Si. В ходе работы были выявлены зависимости механических свойств от состава сплава:
σтек. – предел текучести,
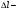 абсолютное удлинение,
абсолютное удлинение,
σпр. – предел прочности;
σтек. =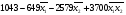
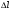
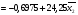
σпр.= 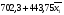
4.1. Оптимальный состав сплава по пределу текучести
Найти оптимальный состав сплава по пределу текучести, т.е. найти такой состав сплава, который обеспечит минимальный предел текучести при следующих ограничениях:
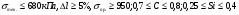 ГОСТ – 84182-80
ГОСТ – 84182-80
Строим график(рис.1).
σтек. min 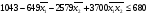
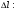
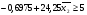
Координаты: 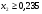
σпр.: 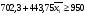
Координаты: 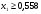
Оптимальный состав сплава при σтек. min является C=0,7%; Si=0,4%.
σтек.= 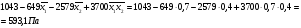
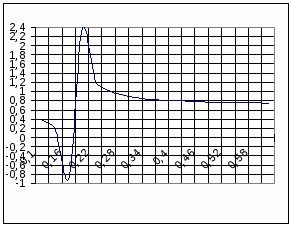
Рис. 2. Нахождение минимума предела текучести
4.2.Оптимальный состав сплава по абсолютному удлинению
Найти оптимальный состав сплава по абсолютному удлинению, т.е. найти такой состав сплава, который обеспечит максимальное абсолютное удлинение при следующих ограничениях:
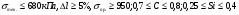 , ГОСТ – 84182-80
, ГОСТ – 84182-80
Строим график(рис.2).
σтек. 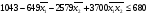
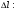 max
max 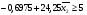
Координаты: 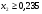
σпр.: 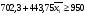
Координаты: 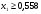
Оптимальный состав сплава при .  max является C=0,7%; Si=0,4%.
max является C=0,7%; Si=0,4%.
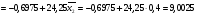

Рис. 3. Нахождение максимального абсолютного удлинения.
4.3. Оптимальный состав сплава по пределу прочности
Найти оптимальный состав сплава по пределу прочности, т.е. найти такой состав сплава, который обеспечит максимальное значение предела прочности при следующих ограничениях:
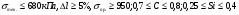 ГОСТ – 84182-80
ГОСТ – 84182-80
Строим график (рис. 3).
σтек. 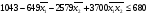
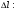
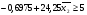
Координаты: 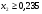
σпр. max 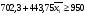
Координаты: 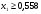
Оптимальный состав сплава при σпр. max является C=0,8%; Si=0,25%.
σпр.= 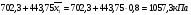

Рис. 3. Нахождение максимального предела прочности.
Как видно, результаты решения задачи графическим методом полностью совпали с решением на компьютере в программе «Эврика» (см. приложение 1) .
Приложение 1
В данном приложении отражено решение задачи оптимизации аналитическим методом с помощью ЭВМ.
***************************************************************
Эврика: Решатель , Верс. 1.0r
Воскр. Ноябрь 23, 1997, 6:47 pm.
Имя файла ввода: C:\TEMP\TMM\EVRIKA\3.EKA
***************************************************************
Y1=1043-649*X1-2579*X2+3700*X1*X2
Y2=-0.6975+24.25*X2
Y3=702.3+443.75*X1
Y1<=680
Y2>=5
Y3>=950
$MIN(Y1)
X1<=0.8
X1>=0.7
X2<=0.4
X2>=.25
***************************************************************
Решение :
Переменные Значения
X1 = .70000000
X2 = .40000000
Y1 = 593.10000
Y2 = 9.0025000
Y3 = 1012.9250
Уровень доверия = 45.8%
Все ограничения удовлетв.
***************************************************************
Эврика: Решатель , Верс. 1.0r
Воскр. Ноябрь 23, 1997, 6:47 pm.
Имя файла ввода: C:\TEMP\TMM\EVRIKA\3.EKA
***************************************************************
Y1=1043-649*X1-2579*X2+3700*X1*X2
Y2=-0.6975+24.25*X2
Y3=702.3+443.75*X1
Y1<=680
Y2>=5
Y3>=950
$MAX(Y2)
X1<=0.8
X1>=0.7
X2<=0.4
X2>=.25
***************************************************************
Решение :
Переменные Значения
X1 = .70522708
X2 = .40000000
Y1 = 597.44370
Y2 = 9.0025000
Y3 = 1015.2445
Уровень доверия = 57.1%
Все ограничения удовлетв.
***************************************************************
Эврика: Решатель , Верс. 1.0r
Воскр. Ноябрь 23, 1997, 6:47 pm.
Имя файла ввода: C:\TEMP\TMM\EVRIKA\3.EKA
***************************************************************
Y1=1043-649*X1-2579*X2+3700*X1*X2
Y2=-0.6975+24.25*X2
Y3=702.3+443.75*X1
Y1<=680
Y2>=5
Y3>=950
$MAX(Y3)
X1<=0.8
X1>=0.7
X2<=0.4
X2>=.25
***************************************************************
Решение :
Переменные Значения
X1 = .80000000
X2 = .25000000
Y1 = 619.05000
Y2 = 5.3650000
Y3 = 1057.3000
Уровень доверия = 53.2%
Все ограничения удовлетв.
Приложение 2
N
С
Si
пр. тек.
абс. удл.
пр. прочн.
1
0,73
0,34
598
7
1010
2
0,76
0,36
589
6
1030
3
0,77
0,32
589
7,3
1010
4
0,81
0,33
623
6
1030
5
0,77
0,37
589
6,7
1050
6
0,79
0,39
559
8
1001
7
0,82
0,34
638
6
1059
8
0,75
0,36
589
6,7
1040
9
0,75
0,32
598
8
1050
10
0,8
0,34
589
4,7
1010
11
0,74
0,32
579
4,7
991
12
0,74
0,31
569
6,7
971
13
0,73
0,32
589
6,7
1010
14
0,75
0,31
579
6
1030
15
0,73
0,33
589
6,3
1030
16
0,73
0,29
579
7,3
991
17
0,75
0,31
579
8,7
1010
18
0,74
0,32
608
6
1030
19
0,72
0,26
598
6
1020
20
0,8
0,28
589
5
1030
21
0,79
0,36
598
6
1040
22
0,78
0,34
579
7
1020
23
0,77
0,32
598
5,3
1001
24
0,75
0,33
471
9,3
893
25
0,77
0,3
589
6,7
1020
26
0,77
0,31
569
6,7
991
27
0,76
0,32
667
6.3
1059
28
0,78
0,35
608
6,7
1020
29
0,74
0,28
598
6
1020
30
0,75
0,32
589
6,7
1020
31
0,73
0,36
589
7,3
1020
32
0,71
0,31
638
6
1030
33
0,74
0,36
589
6,7
1010
34
0,79
0,33
589
6
1030
35
0,75
0,33
608
8
1030
36
0,78
0,34
589
4
1001
37
0,72
0,32
589
6,7
1010
38
0,72
0,33
589
6,7
1001
39
0,73
0,29
589
6
1010
40
0,8
0,38
667
6,7
1079
41
0,75
0,29
647
6,3
1059
42
0,73
0,32
579
7,3
991
43
0,75
0,28
598
7,3
1020
44
0,72
0,34
598
6
1010
45
0,72
0,38
647
7,3
1028
46
0,79
0,31
598
4
1001
47
0,78
0,37
638
6
1030
48
0,73
0,35
598
6,7
1010
49
0,72
0,32
589
7
1010
50
0,71
0,31
540
7,7
942
51
0,76
0,32
549
6
991
52
0,75
0,37
677
14
1128
53
0,77
0,35
598
4,7
991
54
0,79
0,33
647
6
1050
55
0,72
0,33
579
6,7
971
56
0,78
0,33
657
13,3
1079
57
0,75
0,39
687
10,7
1128
58
0,75
0,36
579
8
1010
59
0,75
0,32
657
6,7
981
60
0,76
0,34
608
8
1059
61
0,74
0,33
569
6,7
981
62
0,73
0,31
569
6,7
981
63
0,78
0,36
687
8
1089
64
0,75
0,33
579
8,7
991
65
0,73
0,35
559
6
1001
66
0,73
0,34
549
8
981
67
0,74
0,33
598
7,3
1010
68
0,74
0,32
598
7
1001
69
0,75
0,32
608
5,7
1030
70
0,78
0,32
589
6,7
1030
71
0,79
0,36
618
6,7
1069
72
0,72
0,37
589
10,7
1010
73
0,76
0,39
687
7,3
1079
74
0,75
0,3
598
8
1040
75
0,74
0,33
589
6,7
1020
76
0,74
0,32
598
6,7
1030
77
0,75
0,31
589
6
1020
78
0,75
0,32
579
6
971
79
0,79
0,32
657
6,7
1059
80
0,77
0,3
618
7
1030
81
0,77
0,3
559
6,7
991
82
0,77
0,34
608
6
1079
83
0,79
0,37
687
7,7
1010
84
0,77
0,35
608
7,3
991
85
0,73
0,35
608
4,6
1010
86
0,76
0,36
589
6,7
952
87
0,73
0,33
559
6,6
961
88
0,74
0,32
598
7,3
1010
89
0,79
0,35
618
7,3
971
90
0,76
0,33
589
4
1059
91
0,75
0,33
618
8,7
1050
92
0,79
0,31
638
6,7
961
93
0,73
0,34
569
6,3
1010
94
0,78
0,37
598
6,6
1030
95
0,75
0,35
638
7
1020
96
0,77
0,32
598
5,3
1010
97
0,78
0,37
569
6,3
991
98
0,76
0,32
569
6,7
1010
99
0,73
0,32
559
6,7
1030
100
0,79
0,34
598
6,7
1069
101
0,78
0,37
667
6
991
102
0,72
0,36
569
6,7
1030
103
0,77
0,34
608
6,7
1010
104
0,76
0,32
569
6,7
1020
105
0,76
0,33
569
6
991
106
0,74
0,33
598
6
1050
107
0,78
0,34
598
6,7
1030
108
0,75
0,35
589
7
1059
109
0,78
0,37
657
6,7
1050
110
0,74
0,32
608
4,7
1001
111
0,77
0,34
589
7
1003
112
0,78
0,33
589
6,7
1020
113
0,77
0,36
698
4,7
1040
114
0,77
0,33
628
7
1020
115
0,77
0,39
589
4,7
1010
116
0,73
0,34
598
7
1030
117
0,76
0,36
589
6
1010
118
0,77
0,32
589
7,3
1030
119
0,81
0,33
628
6
1050
120
0,77
0,37
589
6,7
1001
121
0,79
0,39
559
8
1059
122
0,82
0,34
638
6
1040
123
0,75
0,36
589
6,7
1050
124
0,75
0,32
598
8
1010
125
0,8
0,36
589
4,7
991
126
0,74
0,32
579
4,7
971
127
0,74
0,31
569
6,7
1010
128
0,73
0,32
589
6,7
1030
129
0,75
0,31
579
6
1030
130
0,73
0,33
589
6,3
991
131
0,73
0,29
579
7,3
1010
132
0,75
0,31
579
8,7
1030
133
0,74
0,32
608
6
1020
134
0,72
0,26
598
6
1030
135
0,8
0,3
579
5
1040
136
0,79
0,36
598
6
1020
137
0,78
0,34
579
7
1001
138
0,77
0,32
598
5,3
1001
139
0,75
0,33
471
9,3
991
140
0,77
0,3
589
6,7
1059
141
0,77
0,31
569
6,7
1020
142
0,76
0,32
667
6,3
1020
143
0,78
0,35
608
6,7
1020
144
0,74
0,28
598
6
1020
145
0,75
0,32
589
6,7
1030
146
0,73
0,36
589
7,3
1001
147
0,71
0,31
638
6
1030
148
0,74
0,36
589
6,7
1030
149
0,79
0,33
589
6
1001
150
0,75
0,33
608
8
1010
151
0,78
0,34
589
4
1001
152
0,72
0,32
589
6,7
1010
153
0,72
0,33
589
6,7
1030
154
0,73
0,29
589
6
1030
155
0,73
0,32
608
7
1020
156
0,75
0,31
589
6,7
1001
157
0,74
0,3
618
6,3
1050
158
0,78
0,32
598
8
1040
159
0,76
0,3
597
6
1010
160
0,75
0,38
598
6
1059
161
0,78
0,36
618
6,7
1020
162
0,75
0,37
618
5,3
1030
163
0,78
0,3
589
6
961
164
0,75
0,32
569
6,7
1020
165
0,72
0,25
540
7
1010
166
0,79
0,35
608
6,6
1010
167
0,75
0,33
598
6,3
942
168
0,74
0,38
589
5,3
991
169
0,71
0,31
540
7,7
1128
170
0,76
0,32
549
6
991
171
0,75
0,37
677
14
1050
172
0,77
0,35
598
4,7
971
173
0,79
0,33
647
6
1079
174
0,72
0,33
579
6,7
1128
175
0,78
0,33
657
13,3
1010
176
0,75
0,39
687
10,7
981
177
0,75
0,36
579
8
1059
178
0,75
0,32
657
6,7
981
179
0,76
0,34
608
8
981
180
0,74
0,33
569
6,7
1089
181
0,73
0,31
569
6,7
991
182
0,78
0,36
687
8
1001
183
0,75
0,33
579
8,7
981
184
0,73
0,35
559
6
1010
185
0,73
0,34
549
8
1001
186
0,74
0,32
598
7,3
1030
187
0,74
0,32
598
7
1030
188
0,75
0,32
608
5,7
1069
189
0,78
0,32
589
6,7
1010
190
0,79
0,36
618
6,7
1079
191
0,72
0,37
589
10,7
1040
192
0,76
0,39
687
7,3
1020
193
0,75
0,3
598
8
1030
194
0,74
0,33
589
6,7
1020
195
0,74
0,32
598
6,7
971
196
0,75
0,31
589
6
1059
197
0,75
0,32
579
6
1030
198
0,79
0,32
657
6,7
991
199
0,77
0,3
618
7
1059
200
0,77
0,3
559
6,7
1079
201
0,77
0,34
608
6
1010
202
0,79
0,37
687
7,7
991
203
0,77
0,35
608
7,3
1010
204
0,73
0,35
608
4,6
952
205
0,76
0,36
589
6,7
961
206
0,73
0,33
559
6,6
1010
207
0,74
0,32
598
7,3
971
208
0,79
0,35
618
7,3
1059
209
0,76
0,33
589
4
1050
210
0,75
0,33
618
8,7
961
211
0,79
0,31
638
6,7
1020
212
0,73
0,34
569
6,3
1030
213
0,78
0,37
598
6,6
1020
214
0,75
0,35
638
7
971
215
0,77
0,32
598
5,3
991
216
0,78
0,37
569
6,3
1010
217
0,76
0,32
569
6,7
1030
218
0,73
0,32
559
6,7
1069
219
0,79
0,34
598
6,7
991
220
0,78
0,37
667
6
1030
221
0,72
0,36
569
6,7
1010
222
0,77
0,34
608
6,7
1020
223
0,76
0,32
569
6,7
991
224
0,76
0,33
569
6
1050
225
0,74
0,33
598
6
1030
226
0,78
0,34
598
6,7
1059
227
0,75
0,35
589
7
1050
228
0,78
0,37
657
6,7
1001
229
0,74
0,32
608
4,7
1003
230
0,77
0,34
589
7
1020
231
0,78
0,33
589
6,7
1040
232
0,77
0,36
698
4,7
1020
233
0,77
0,33
628
7
1010
234
0,77
0,39
589
4,7
1030
235
0,73
0,34
598
7
1010
236
0,76
0,36
589
6
1030
237
0,77
0,32
589
7,3
1001
238
0,81
0,33
628
6
1001
239
0,77
0,37
589
6,7
1059
240
0,79
0,39
559
8
1040
241
0,82
0,34
638
6
1050
242
0,75
0,36
589
6,7
1010
243
0,75
0,32
598
8
991
244
0,8
0,34
589
4,7
971
245
0,74
0,32
579
4,7
1010
246
0,74
0,31
569
6,7
1030
247
0,73
0,32
589
6,7
1030
248
0,75
0,31
579
6
991
249
0,73
0,33
589
6,3
1010
250
0,73
0,29
579
7,9
1030
251
0,75
0,31
579
8,7
1020
252
0,74
0,32
608
6
1030
253
0,72
0,26
598
6
1040
254
0,8
0,3
589
5
1001
255
0,79
0,36
598
6
893
256
0,78
0,34
579
7
941
257
0,77
0,32
598
5,3
991
258
0,75
0,33
471
9,3
1059
259
0,77
0,3
589
6,7
1020
260
0,77
0,31
569
6,7
1020
261
0,76
0,32
667
6,3
1020
262
0,78
0,35
608
6,7
1020
263
0,74
0,28
598
6
1030
264
0,75
0,32
589
6,7
1001
265
0,73
0,36
589
7,3
1030
266
0,71
0,31
638
6
1030
267
0,74
0,36
589
6,7
1001
268
0,79
0,33
589
6
1010
269
0,75
0,33
608
8
971
270
0,78
0,34
589
4
1010
271
0,72
0,32
589
6,7
1030
272
0,72
0,33
589
6,7
1030
273
0,73
0,29
589
6
1020
274
0,73
0,32
608
7
1001
275
0,75
0,31
589
6,7
1050
276
0,74
0,3
618
6,3
1040
277
0,78
0,32
598
8
1010
278
0,76
0,29
597
6
1059
279
0,75
0,38
598
6
1020
280
0,78
0,36
618
6,7
1030
281
0,75
0,37
618
5,3
961
282
0,78
0,31
589
6
1020
283
0,75
0,32
569
6,7
1010
284
0,72
0,25
540
7
1010
285
0,79
0,35
608
6,6
942
286
0,75
0,33
598
6,3
991
287
0,74
0,38
589
5,3
1128
288
0,71
0,31
540
7,7
991
289
0,76
0,32
549
6
1050
290
0,75
0,37
566
14
971
291
0,77
0,35
598
4,7
1079
292
0,79
0,33
647
6
1128
293
0,72
0,33
579
6,7
1010
294
0,78
0,33
657
13,3
981
295
0,75
0,39
687
10,7
1059
296
0,75
0,36
579
8
981
297
0,75
0,32
657
6,7
981
298
0,76
0,34
608
8
1089
299
0,74
0,33
569
6,7
991
300
0,73
0,31
569
6,7
1001
301
0,78
0,36
687
8
981
302
0,75
0,33
579
8,7
1010
303
0,73
0,35
559
6
1001
304
0,73
0,34
549
8
1030
305
0,74
0,33
598
7,3
1030
306
0,74
0,32
598
7
1069
307
0,75
0,32
608
5,7
1010
308
0,78
0,32
589
6,7
1097
309
0,79
0,36
618
6,7
1040
310
0,72
0,37
589
10,7
1020
311
0,76
0,39
687
7,3
1030
312
0,75
0,3
597
8
1020
313
0,74
0,33
589
6,7
971
314
0,74
0,32
598
6,7
1059
315
0,75
0,31
589
6
1030
316
0,75
0,32
579
6
991
317
0,79
0,32
657
6,7
1059
318
0,77
0,3
618
7
1079
319
0,77
0,3
559
6,7
1010
320
0,77
0,34
608
6
991
321
0,79
0,37
687
7,7
1010
322
0,77
0,35
608
7,3
952
323
0,73
0,35
608
4,6
961
324
0,76
0,36
589
6,7
1010
325
0,73
0,33
559
6,6
971
326
0,74
0,32
598
7,3
1059
327
0,79
0,35
618
7,3
1050
328
0,76
0,3
589
4
961
329
0,75
0,33
618
8,7
1010
330
0,79
0,31
638
6,7
1030
331
0,73
0,34
569
6,3
1020
332
0,78
0,37
598
6,6
971
333
0,75
0,35
638
7
991
334
0,77
0,32
598
5,3
1010
335
0,78
0,37
569
6,3
1030
336
0,76
0,32
569
6,7
1069
337
0,73
0,32
559
6,7
991
338
0,79
0,34
598
6,7
1030
339
0,78
0,37
667
6
1010
340
0,72
0,36
569
6,7
1020
341
0,77
0,34
608
6,7
991
342
0,76
0,32
569
6,7
1050
343
0,76
0,33
569
6
1030
344
0,74
0,33
598
6
1059
345
0,78
0,34
598
6,7
1050
346
0,75
0,35
589
7
1001
347
0,78
0,37
657
6,7
1003
348
0,74
0,32
608
4,7
1020
349
0,77
0,34
589
7
1040
350
0,78
0,33
589
6,7
1020
351
0,77
0,36
698
4,7
1010
352
0,77
0,33
628
7
1030
353
0,77
0,39
589
4,7
1010
354
0,73
0,34
598
7
1030
355
0,76
0,36
589
6
1050
356
0,77
0,32
589
7,3
1001
357
0,81
0,26
628
6
1059
358
0,77
0,37
589
6,7
1040
359
0,79
0,39
559
8
1050
360
0,82
0,34
638
6
1010
361
0,75
0,36
589
6,7
991
362
0,75
0,32
598
8
971
363
0,8
0,34
589
4,7
1010
364
0,74
0,32
579
4,7
1030
365
0,74
0,31
569
6,7
1010
366
0,73
0,32
589
6,7
991
367
0,75
0,31
579
6
1010
368
0,73
0,33
589
6,3
1030
369
0,73
0,29
579
7,3
1020
370
0,75
0,31
579
8,7
1020
371
0,74
0,32
608
6
1030
372
0,72
0,26
598
6
1040
373
0,8
0,31
589
5
1020
374
0,79
0,36
598
6
1001
375
0,78
0,34
579
7
893
376
0,77
0,32
598
5,3
1020
377
0,75
0,33
471
9,3
991
378
0,77
0,3
589
6,7
1059
379
0,77
0,31
569
6,7
1020
380
0,76
0,32
667
6,3
1020
381
0,78
0,35
608
6,7
1020
382
0,74
0,28
598
6
1020
383
0,75
0,32
589
6,7
1030
384
0,73
0,36
589
7,3
1001
385
0,71
0,31
638
6
1030
386
0,74
0,36
589
6,7
1030
387
0,79
0,33
589
6
1001
388
0,75
0,33
608
8
1010
389
0,78
0,34
589
4
1001
390
0,72
0,32
589
6,7
1010
391
0,72
0,33
589
6,7
1030
392
0,73
0,29
589
6
1030
393
0,73
0,32
608
7
1020
394
0,75
0,31
589
6,7
1001
395
0,74
0,3
618
6,3
1050
396
0,78
0,32
598
8
1040
397
0,76
0,29
597
6
1010
398
0,75
0,38
598
6
1059
399
0,78
0,36
618
6,7
1020
400
0,75
0,37
618
5,3
981

Нравится материал? Поддержи автора!
Ещё документы из категории химия:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ