Простейшая схема одноэлектронной теории
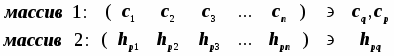
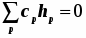
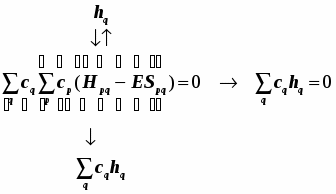
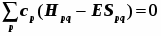
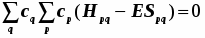

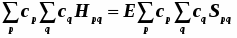

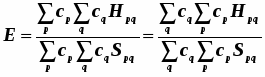
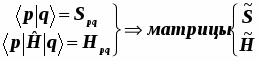
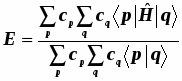
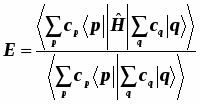
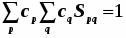

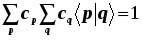

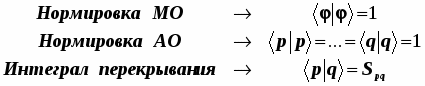
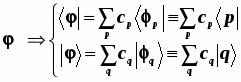
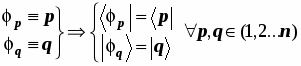
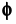
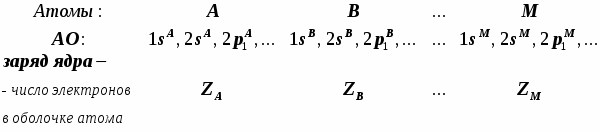 Простейшая схема одноэлектронной теории.
Простейшая схема одноэлектронной теории.
Молекула это система, содержащая несколько ядер и электронов.
Уравнение Шрёдингера для такой системы многомерное, число переменных в нём всегда больше трёх, и аналитически точные решения недостижимы. Рассчитывать можно лишь на построение приемлемой приближённой теории. Это и плохо, и хорошо.
Плохо потому, что любые приближения всегда субъективны и зависят от вкуса и возможностей исследователя даже тогда, когда внешне кажутся безупречными. Хорошо же потому, что приближения никогда не вводятся бездумно.
Приходится выяснять и увязывать между собою множество физических и математических деталей, выбирая при этом и физически корректную, и наиболее рациональную схему построения теории. Это непросто. Однако кем-то высказана замечательная мысль о том, что в стремлении к истине сам процесс едва ли не важнее конечного результата.
Наш случай сравнительно счастливый. Произошло так, что электронно-вычислительная техника и квантовая механика многоэлектронных молекул развивались практически параллельно, и математический аппарат со временной квантовой механики молекул оказался идеально приспособлен к воз можностям современной информатики. Удалось сделать очень много (но далеко не всё!).
Квантовая механика атомов и молекул привела к построению современной теории химической связи в её количественной, полуколичественной формах.
Это вычислительно точная, полуэмпирическая-компромиссная по сложности расчётов, обслуживающая эксперимент-прикладная и доступная для широкого пользователя, и качественная концептуально-систематизационная.
Основную роль в построении качественной теории валентности сыграло обобщение данных множества квантово-химических расчётов и выявление специфических для гомологических и структурных рядов соединений количественных признаков и критериев, посредством которых удаётся обобщить закономерности электронных свойств атомно-молекулярных систем. Многие из таких критериев не имеют привычного физического смысла и оказываются лишь удобными для корреляций численными комбинациями, обслуживающими ту или иную химическую концепцию.
Для их систематизации создана своя развитая, гибкая, вполне самостоятельная и во многом независимая от иных физических дисциплин система понятий образов и математических соотношений. В них уже почти не присутствуют признаки родительских разделов физики: механики, оптики, электродинамики. Они заменены разнообразными обобщёнными индексами и признаками молекулярной структуры.
Соответствующая терминология образует язык современной теории валентности и теоретической химии. Удивительнее всего то, что фундаментом всего этого гигантского мира теоретической химии оказывается единственная математическая структура – уравнение Шрёдингера.
Всё же грандиозная проблема количественного прогнозирования молекулярных свойств с точностью, не уступающей эксперименту, далека от завершения. Множество важнейших для химии задач ещё ожидают решения.
Система приближений.
Их цель – упрощение процедуры поиска решений уравнения Шрёдингера, а также облегчение теоретической интерпретации получаемых результатов.
Приближения вводятся для упрощения: 1) гамильтониана, 2) волновых функций.
При построении простейшей теории приближённый гамильтониан строится независимым от вида конечных решений – искомых приближённых волновых функций. Исходным выбором приближённого гамильтониана полностью определён и результат - вид конечных волновых функций. Такая теория может быть построена для одного «пробного» электрона.
При построении уточнённой теории выражения для гамильтониана и для волновых функций взаимозависимы. Слагаемые гамильтониана представляются в виде выражений, зависящих от элементов искомых волновых функций. Такие задачи решаются приближённым итерационным способом. Общая теоретическая схема, обеспечивающая решение такой оптимизационной задачи, называется методом самосогласованного поля (метод ССП). Теория, в рамках которой развивается процедура ССП, наиболее строгая и общая, и всегда многоэлектронная.
Приближение Борна Оппенгеймера.
Ядерный остов молекулы считается неподвижным. Все длины связей и все валентные углы в расчёте принимаются постоянными.
Фиксированное взаимное положение атомных ядер в молекуле для осуществлении расчёта можно задать двумя способами.
Во-первых, задают какую-то систему координат, определяют её центр и задают ориентацию осей (обычно декартовых). В центр координат помещают один из атомов - обычно это атом с максимальным координационным числом.
Во-вторых, по какой-либо схеме, по определённым правилам, перечисляют межатомные расстояния и валентные углы между связями. Сводная таблица геометрических параметров называется Z-матрицей.
В современных программах последовательность связей в молекуле очень легко задать графически, манипулируя «мышкой» непосредственно на экране монитора.
Одноэлектронное приближение.
Движение каждого отдельного электрона рассматривается независимо от других и
описывается одноэлектронным уравнением Шрёдингера.
Поля прочих электронов искусственно учитываются посредством корректирующих слагаемых в суммарной потенциальной энергии.
При необходимости (в неэмпирических расчётах) для уточнённого описания всего
электронного коллектива, всей электронной оболочки молекулы используется система взаимосвязанных одноэлектронных уравнений.
Одноэлектронные состояния (волновые функции) называют орбиталями. В атомах - орбитали атомные (АО), в молекуле - молекулярные (МО). Одна из основных задач теории молекул – вычисление свойств МО.
Оно состоит в расчёте спектра уровней и спектра волновых функций МО (составов).
Спектры одноэлектронных состояний и уровней энергии одинаковы у всех электронов.
3. Приближение ЛКАО МО.
Всякая молекулярная орбиталь может быть представлена в виде линейной комбинации АО атомов, образующих молекулу.
Эта линейная комбинация (ЛК) – ряд, элементами которого являются АО, является одной из простейших и наиболее удачных аппроксимаций МО. Так возникает один из наиболее современных методов современной теоретической химии. Его наименование выражается знаменитой аббревиатурой «МО ЛКАО».
4. Базис и его свойства.
Массив АО, из которых конструируются МО, называется базисом. От вида базисных АО существенно зависят качества теоретической модели.
Длина базиса. Ограниченный базис.
Количество АО у каждого атома, строго говоря, не ограничено. Идеальный базис бесконечно длинный. И результирующие ЛКАО были бы бесконечной длины. Такой вид МО неудобен. Принято использовать ограниченный базис. В нём конечное число АО.
Базис валентный (Валентное приближение).
Предполагают, что основные свойства оптических электронов молекулы формируются в пределах лишь той части базисного набора АО каждого из атомов, которая заселена оптическими - валентными электронами атомов. В этом приближении ограниченный базис включает лишь валентные АО всех атомов молекулы.
Базисные функции.
Базисные АО можно построить в различной аналитической форме. Достаточно распространены
-слейтеровские АО;
-гауссовы АО.
Распространены и такие методы, где обращения к явному виду базиса избегают.
Гамильтониан
Простейшее упрощение молекулярного гамильтониана, непосредственно вытекает из приближения Борна-Оппенгеймера. На первичной стадии расчёта игнорируется движение ядер. Рассматривается исключительно движение электронов в поле неподвижного остова.
В простых вариантах теории МО ЛКАО вводится максимально возможное упрощение, в котором многоэлектронный гамильтониан представляется в виде суммы одноэлектронных гамильтонианов. Возникающие матричные элементы вычисляются лишь частично или параметризуются.
5.1. Эффективный гамильтониан (в простейших расчётах МО ЛКАО).
Считается, что одноэлектронный гамильтониан можно привести к форме, полностью независимой от состояний всех прочих электронов оболочки. Такой гамильтониан называется эффективным одноэлектронным, и он приводит к простейшей одноэлектронной схеме полуэмпирической теории МО ЛКАО. При таком подходе исследование ограничено и не может выйти за пределы набора орбиталей единственной «пробной» частицы, и лишь из их свойств выводятся все доступные электронные свойства молекулы.
Этот подход не является количественно точным, но именно он позволил накопить огромную фундаментальную информацию о качественных признаках химической связи.
Так возникает схема многоэлектронной теории молекулярных состояний. В максимально развитом виде так строится неэмпирическая теория МО ЛКАО. Все неэмпирические методы называются методами ab initio (-с начала) и претендуют на максимальную теоретическую корректность. Объектами всех вычислительных преобразований и источником всей физической информации об электронной оболочке молекулы являются математически достаточно сложные полные многоэлектронные волновые функции, учитывающие принцип Паули.
6. Процедура расчёта МО ЛКАО
Молекула состоит из атомов, которые перечислим, нумеруя в любом порядке, но далее всюду соблюдая принятую нумерацию:
Количество АО у каждого свободного атома не ограничено, и, конечно, наилучшим базисом был бы такой, в котором содержалось максимально возможное количество функций, однако не существует возможности использовать базис бесконечной длины в практических расчётах. Поэтому во всех, даже наиболее совершенных, расчётах используется ограниченное количество базисных функций АО. При выборе базиса используются различные способы ограничения его длины. В более совершенных вариантах теоретических расчётов МО ЛКАО базисные наборы достаточно велики. В более простых приближениях применяют более ограниченные базисные наборы АО.
Наиболее простым и потому распространённым является валентное приближение. Оно состоит в том, для расчёта электронного строения молекулы используют базис, включающий от каждого атома только АО внешнего оптического слоя. Главное квантовое число всех этих АО одно и то же, но при необходимости базис можно расширить за счёт включения и АО близлежащих подуровней с соседними значениями главного квантового числа. Рассчитываемая часть спектра МО заселяется оптическими электронами, находящимися на внешних валентных АО атомов.
У каждого атома в нейтральном зарядовом состоянии число электронов равно его порядковому номеру в Системе Менделеева. В начале расчёта атомы нумеруются. Все внутренние АО, уровни которых лежат ниже оптических АО, считаются атомными, т.е. их вид считается таким же, как и в свободном атоме, и это недалеко от истины. Набор АО последовательно нумеруется.
Согласно математической схеме квантовой механики по Дираку, всякая волновая функция представляется двумя неразрывно связанными образами-«компонентами»: бра- и кет-векторами.... Это в чём-то напоминает ситуацию с комплексными числами, каждое из которых само по себе ничего не представляет, обретая смысл лишь в паре со своим комплексно сопряжённым двойником. Похожим образом обстоит дело и с бра-кет- векторами Дирака. Каждый из них неотделим от своего двойника, и лишь вместе они служат основой очень элегантного и компактного построения квантовой механики. Это выглядит следующим образом. Каждой базисной АО отвечают два вектора: бра-вектор и кет-вектор АО, а именно:
«Бра-кет» - символы это не что иное, как «ско- бки»- символы (от англ. brackets-скобки).
Каждый из этих векторов МО представляется в виде разложения в ряд и при этом:
- бра-векторы МО построены только из бра-векторов АО.
- кет-векторы МО построены только из кет-векторов АО.
В наших расчётах приходится часто иметь дело с массивами однотипных объектов. Условимся опускать многократно повторяющиеся символы. Так, производя вычисления, нет смысла повторять всё время один и тот повто ряющийся символ в последовательности базисных АО:. С таким же успехом можно ограничиться просто перечислением индексов: 1,2,3,...p,...q,..., в нужном контексте идентифицируя с ними сами АО. В итоге получается предельно компактная запись:
-
АО и их
обозначения
в виде индек сов
Бракет-символы
АО
Пределы изменения
индексов АО
МО
Бра-кет-
символы
МО
Разложения
МО ЛКАО
Базис:; МО:;
Точно так же, как введены индексные обозначения для базисных АО, ничто не мешает при необходимости ввести индексные обозначения и для МО... Свойства МО и составляющих их БАО следующие:-
Введём понятие молекулярного эффективного одноэлектронного гамильтониана.
Молекулярные орбитали являются его собственными функциями.
3) или эквивалентно, т.е.
Здесь представлено скалярное произведение двух векторов-массивов вида

Нравится материал? Поддержи автора!
Ещё документы из категории химия:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ