Равновесные и поляризационные диаграммы потенциал-pH
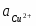
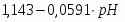
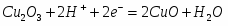
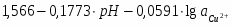
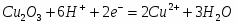
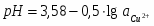
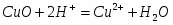
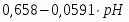
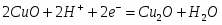
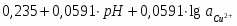
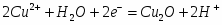
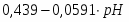
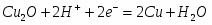
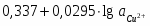
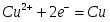
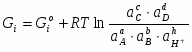
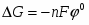

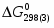
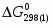
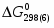
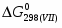
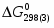
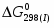
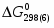
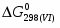
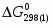
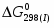
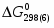
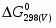
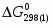
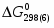
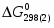
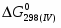
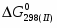
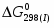
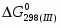
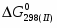
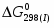
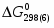
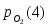

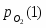
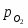
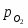
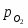
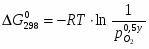
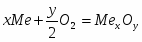
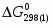
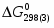
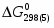
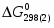
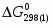
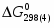
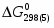
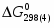
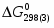
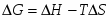
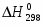
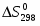
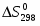
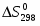
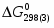
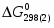
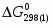
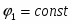
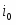
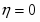
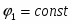
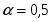
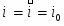
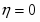
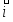

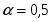
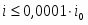
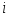
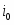
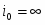
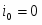
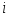
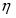
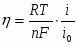
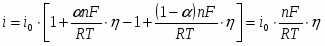
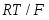
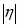
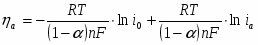
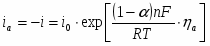
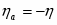
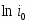
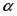
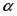
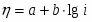
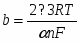
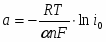
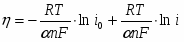
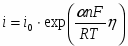
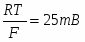
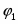
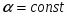
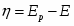
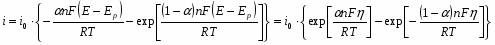
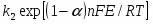
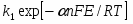
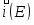
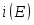
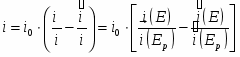
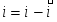
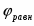
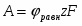
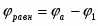
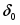
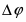
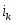
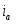
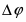
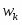
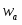
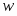
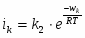
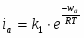
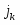
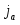
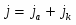
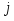
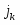
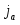
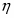
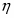
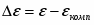
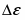
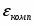
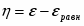
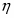
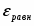
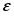
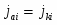
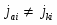
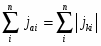
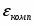
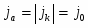
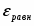
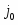
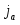
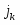
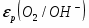
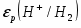
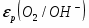
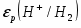
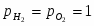
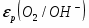
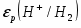
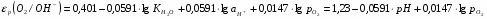
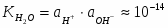
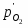
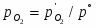
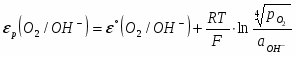
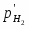
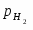
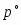
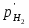
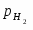
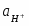
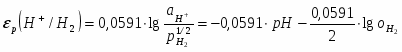
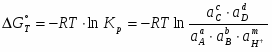
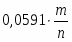
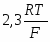
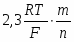
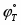
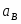
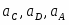
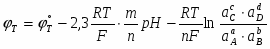
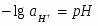
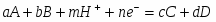
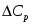
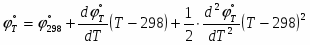
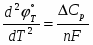
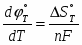
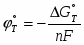
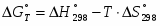
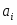
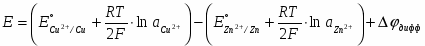
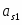
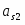
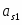
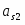
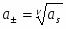
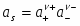
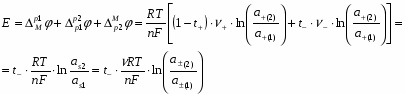
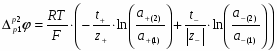
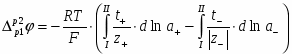
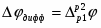
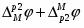
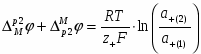
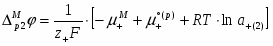
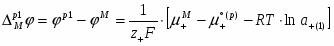
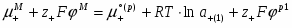
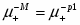
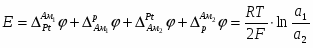
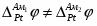
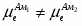
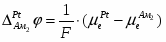
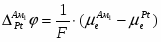
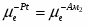
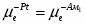
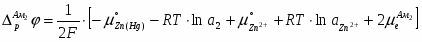
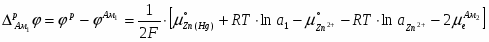
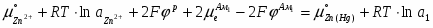
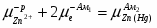
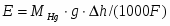
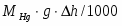
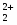
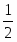
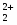
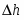
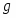
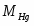
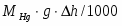
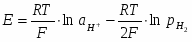
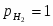
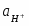
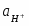
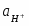
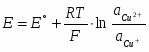
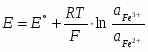
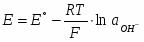
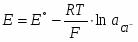
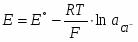
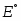
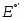
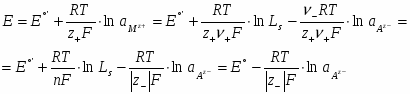
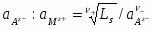
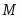
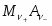
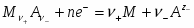
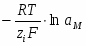
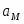
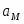
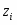
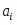
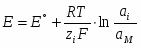
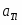
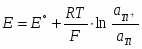
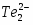
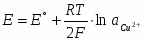


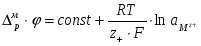
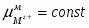
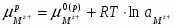
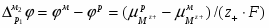
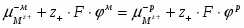
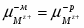
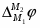
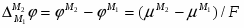
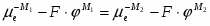
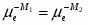
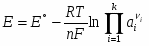
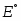
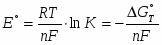
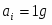
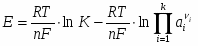
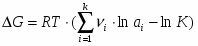
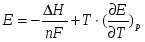
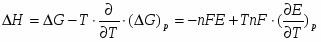
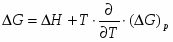
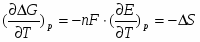
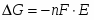
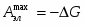
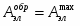
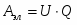
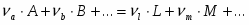 ГОУ ВПО “ЧЕЛЯБИНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ”
ГОУ ВПО “ЧЕЛЯБИНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ”
Химический факультет
Кафедра аналитической и физической химии
Курсовая работа:
РАВНОВЕСНЫЕ И ПОЛЯРИЗАЦИОННЫЕ ДИАГРАММЫ ПОТЕНЦИАЛ-pH
Челябинск 2010 г.
ВВЕДЕНИЕ
В настоящее время большую важность имеет возможность оценивать устойчивость металлов и их сплавов к коррозии в тех или иных условиях. Эту возможность позволяет реализовать на практике применение равновесных и поляризационных диаграмм в координатах потенциал – pH.
На основе диаграмм электрохимической устойчивости (равновесных диаграмм потенциал – pH или диаграмм Пурбе) можно делать выводы о возможности устойчивости металлов и их сплавах, условиях образования пассивирующей пленки, появлении питтингов и перехода металла в ионы.
Однако, у диаграмм Пурбе есть недостаток, заключающийся в том, что в реальности состояние электрохимического равновесия не достигается.
Для того, чтобы описать коррозионно-электрохимическое поведение металлов в реальных условиях, используется поляризационная диаграмма потенциал – рН.
Поляризационная диаграмма основана на реальных поляризационных кривых и является «коррозионным паспортом» данного сплава.
Целью данной работы является изучение равновесных и поляризационных диаграмм потенциал – pH, принципах их построения и анализа, а также расчет и построение диаграммы электрохимической устойчивости для системы Cu – H2O.
1. ЛИТЕРАТУРНЫЙ ОБЗОР
1.1 Термодинамика электрохимических систем и электродных процессов. Условная водородная шкала. Правило знаков ЭДС и электродных потенциалов. Электрохимический потенциал. Электрохимические равновесия
Пусть в электрохимической системе обратимо и изотермически протекает процесс:
(1.1.1)
Работа по перемещению электрического заряда равна:
(1.1.2)
Для обратимой реакции:
(1.1.3)
Полезная работа обратимого процесса максимальна и равна убыли изобарного потенциала системы, т. е:
(1.1.4) при p,T=const
Изменение изобарного потенциала вызвано совокупностью электрохимических реакций на электродах, т. Е. суммарной химической реакцией или другими физико-химическими процессами (растворение, выравнивание концентраций, фазовое превращение и др.).
С учетом того, что U=E и , и формул (1.1.2), (1.1.3) и (1.1.4), получаем:
(1.1.5)
Производная ΔG по температуре:
(1.1.6)
Таким образом, измерив ЭДС системы и ее температурный коэффициент, можно легко найти величины ΔG и ΔS для суммарного процесса, протекающего в электрохимической системе. Этот процесс является самопроизвольным, следовательно, ΔG < 0.
Важную термодинамическую характеристику этого процесса – изменение энтальпии – вычисляют по уравнению Гиббса – Гельмгольца.
(1.1.7)
(1.8)
ЭДС электрохимической системы находят по уравнению:
(1.9)
Чтобы связать ЭДС с константой равновесии, используют изотерму Вант – Гоффа. Если предположить, что реакция (1.1.1) протекает в жидком растворе, то:
(1.1.10)
С учетом (1.1.5) и (1.1.10) получается:
(1.1.11)
При получаем , где - это стандартная величина ЭДС системы.
С учетом этого получают общее выражение ЭДС электрохимической цепи или уравнение Нернста:
(1.1.12)
Приведенные выше уравнения дают возможность вычислить величины ΔG и К по экспериментальным значениям Е и, наоборот, рассчитать Е, зная термодинамические характеристики химической реакции.
Таким образом, измерение ЭДС электрохимических элементов и цепей является очень простым и точным методом вычисления термодинамических характеристик химических реакций и некоторых важных физико-химических процессов в растворах. Нельзя забывать, что этот метод подходит только для тех случаев, когда процесс в электрохимической системе обратим.
В связи с тем, что в настоящее время нет прямых экспериментальных и расчетных методов определения отдельных скачков потенциала на границе раздела фаз в гальваническом элементе, значение потенциала отдельных электродов приводят относительно потенциала какого-либо стандартного электрода, потенциал которого условно принимают равным 0 при любых температурах. Таким стандартным электродом, или электродом сравнения, является обратимый водородный электрод, в котором газообразный водород находится при давлении 1 атм. и насыщает платиновый электрод. Раствор, в который погружен водородный электрод, содержит ионы водорода (гидроксония), причем активность H+ равна единице.
Согласно Международной конвенции (1953 г.), электродным потенциалом электрода называется ЭДС элемента, составленного из этого электрода (справа) и стандартного водородного электрода (слева).
Например, для нахождения электродного потенциала цинка составляют элемент
(+) Pt, H2│H+, aq║Zn2+, aq│Zn (–) [1].
Пусть на границе электрод – раствор в результате протекания процессов с участием заряженных и незаряженных частиц устанавливается равновесие, описываемое уравнением (1.1).
Рассмотрим два примера установления электрохимического равновесия на границе раздела фаз.
1. Граница двух различных металлов.
При установлении равновесия на этой границе происходит выравнивание электрохимических потенциалов электронов в металлах М1 и М2.
Условие равновесия имеет вид
(1.1.13)
(1.1.14)
Отсюда для гальвани-потенциала на границе металл – металл получают выражение:
(1.1.15)
Таким образом, в условиях равновесия работа перенесения электрона из одного металла в другой равна нулю, но работа переноса единицы воображаемого заряда, т. е. , отлична от нуля, поскольку химические потенциалы электрона в различных металлах неодинаковы.
2. Граница металла М с раствором, содержащим ионы этого же металла. При установлении равновесия происходит выравнивание электрохимических потенциалов ионов Mz+ в растворе и в кристаллической решетке металла.
При равновесии:
(1.1.16)
(1.1.17)
Гальвани-потенциал на границе металл – раствор соответствующей соли имеет вид:
(1.1.18)
Поскольку , а , уравнение (1.1.18) можно переписать в виде:
(1.1.19)
Уравнение (1.1.19) – это частный случай уравнения Нернста для отдельного гальвани-потенциала. Таким образом, в условиях рассмотренного электрохимического равновесия работа перенесения иона Mz+ из металла в раствор или обратно равна нулю. Гальвани-петенциал зависит от концентрации потенциалопределяющих ионов Mz+ и также может быть сведен к нулю. Однако невозможность измерить гальвани-потенциал не позволяет установить, при какой именно концентрации Mz+ =0.
Правильно разомкнутая электрохимическая цепь, на концах которой можно измерить электрическую разность потенциалов, всегда должна заканчиваться одинаковыми по своему химическому составу металлами. Электрохимическая цепь является равновесной при условии, что электрохимическое равновесие наблюдается на каждой фазовой границе, а разность потенциалов на концах цепи Е скомпенсирована разностью потенциалов от внешнего источника цепи.
Из (1.1.5):
E=–ΔG/nF (1.1.20)
Т.е. разность потенциалов на концах равновесной электрохимической цепи однозначно связана с изменением свободной энергии Гиббса в ходе соответствующей химической реакции. Величина E и называется ЭДС, т.е. электродвижущей силой электрохимической цепи. Уравнение (1.1.20) применимо только в том случае, если на всех фазовых границах устанавливается равновесие, в противном случае разность потенциалов на концах цепи не равна ЭДС и уравнение оказывается неприменимым [2].
1.2 Классификация электродов. Классификация электрохимических цепей
Классификация электродов
Классификация электродов проводится по химической природе веществ Ox и Red, участвующих в электродном процессе.
Электродом 1-ого рода называют систему, в которой восстановленной формой является металл электрода, а окисленной формой – простые или комплексные ионы этого же металла.
Примером может служить система Cu2++2e-=Cu, для которой:
(1.2.1)
Как правило, электроды 1-ого рода обратимы по катиону, т.е. их потенциал является функцией активности катиона. Однако, есть небольшое количество электродов 1-ого рода, обратимых по аниону, например 2Te+2e-=, для которого
(1.2.2)
К электродам 1-ого рода относятся амальгамные электроды, в которых восстановленной формой служит амальгама какого-либо металла, а окисленной – ионы того же металла:
Tl++e-(Hg)=Tl(Hg)
Поскольку в таких системах может изменяться концентрация как Ox, так и Red, то
(1.2.3)
Здесь - активность таллия в амальгаме.
Общая формула для потенциала электрода 1-ого рода имеет вид:
(1.2.4)
Здесь - активность потенциалопределяющих ионов в растворе, - зарядовое число потенциалопределяющих ионов с учетом знака; - активность соответствующего металла. Для чистых металлов =const и соответствующий член вводится в стандартный потенциал.
Электродом 2-ого рода называют систему, в которой металл покрыт слоем его труднорастворимой соли (или оксида), а раствор содержит анионы этой соли (для оксида – ионы OH-):
Таким образом, окисленной формой здесь является труднорастворимая соль , а восстановленная форма представлена металлом и анионом . Потенциал электрода 2-ого рода определяется активность ионов соответствующего металла , которую можно выразить через произведение растворимости соли Ls и активность аниона . Таким образом, уравнение Нернста для электродов 2-ого рода принимает вид:
(1.2.5)
Здесь - стандартный потенциал системы Мz+/М; - стандартный потенциал электрода 2-ого рода. Как следует из уравнения (1.2.5), электрод 2-ого рода является обратимым по аниону.
Рассмотрим некоторые примеры электродов 2-ого рода.
Хлорсеребряный электрод: AgCl+e-=Ag+Cl-
(1.2.6)
Каломельный электрод: Hg2Cl2+2e-=2Hg+2Cl-
(1.2.7)
Ртутно-оксидный электрод: Hg2O+2e-+H2O=2Hg+2OH-
(1.2.8)
Во всех системах, отвечающих электродам 1 и 2-ого, одним из компонентов восстановленной формы служит металл электрода. Если же инертный металл электрода не участвует в полуреакциях, а является только передатчиком электронов между Ox и Red, то такие системы называют окислительно-восстановительными электродами или редокс-системами.
Например, система:
Fe3++e-=Fe2+,
Cu2++e-=Cu+,
С платиновым электродом в качестве инертного переносчика электронов между Ox и Red.
Среди окислительно-восстановительных электродов выделяют газовые электроды. Газовый электрод состоит инертного металла (часто платины или платинированной платины), к которому подводится электрохимически активный газ. Молекулы газа адсорбируются на поверхности металла, распадаясь при этом на атомы, а адсорбированные атомы участвуют уже непосредственно в электродной реакции. Поскольку между молекулами газовой фазы и адсорбированными атомами устанавливается равновесие, то при записи электродного равновесия промежуточное адсорбционное состояние часто опускают. Примером газового электрода, обратимого по катиону, является водородный электрод, на поверхности которого устанавливается равновесие: H++e-=1/2H2.
Потенциал водородного электрода – это ЭДС цепи:
Pt, H2(p=1)│H3O+(=1) ¦¦ H3O+()│ H2(p), Pt
Если в правой части цепи положить =1 и , то цепь окажется полностью симметричной и ее ЭДС должна равняться нулю. Следовательно,
(1.2.9)
Классификация электрохимических цепей.
Электрохимические цепи обычно классифицируют по двум признакам:
по источнику электрической энергии
по наличию или отсутствию в цепи границы двух различных растворов: соответственно цепи с переносом и без переноса.
В физических цепях источником электрической энергии служит различие в физическом состоянии двух одинаковых по своему химическому составу электродов. Эти электроды погружены в один и тот же раствор и при работе цепи электрод, находящийся в менее устойчивом состоянии, переходит в более устойчивое состояние.
Физические цепи – цепи без переноса – подразделяются на аллотропические и гравитационные.
Аллотропические цепи – это цепи, в которых менее устойчивое состояние одного электрода обусловлено тем, что он изготовлен из метастабильной модификации данного металла.
Гравитационные цепи были впервые реализованы русским электрохимиком Р. А. Колли (1875). Например, гравитационная цепь, состоящая из двух ртутных электродов в растворе Hg2(NO3)2. Ее левый электрод с более высоким уровнем ртути обладает большим запасом потенциальной энергии по сравнению с правым электродом. Этот избыток потенциальной энергии в расчете на 1 г-экв металлической ртути составляет , где - молекулярная масса ртути; - ускорение силы тяжести; - разность уровней ртути. При работе цепи на левом электроде происходит растворение ртути;
Hg→Hg+e-
а на правом, наоборот, разряд ионов Hg:
Hg+e- →Hg
В результате этих двух электродных процессов происходит перенос металлической ртути из левой части в правую, который направлен на выравнивание уровней ртути. При этом перенос 1 г-экв ртути соответствует прохождению через систему 1 фарадея и электрической работе EF. Поскольку источником этой энергии является потенциальная энергия , то ЭДС гравитационной цепи равна:
(1.2.10)
Из-за малых величин Е гравитационные цепи не имеют практического значения. Они представляют интерес как пример, иллюстрирующий законы превращения энергии.
В концентрационных цепях оба электрода идентичны как по физическому состоянию, так и по химической природе участников окислительно-восстановительных процессов; они отличаются только концентрацией компонентов Ox или Red. Источником электрической энергии является разность свободных энергий Гиббса, обусловленная различными активностями одних и тех же химических компонентов. Концентрационные цепи можно приготовить из амальгам разных концентраций в одном и том же растворе; из одинаковых электродов 1 или 2-ого рода, находящихся в растворах разной концентрации; из одинаковых газовых электродов, работающих при разных давлениях газов.
Различают концентрационные цепи без переноса, т.е. без границы двух растворов, и с переносом, когда имеется такая граница. Цепи, построенные из двух амальгамных электродов с разной концентрацией амальгам или из двух газовых электродов с разным давлением газа, содержат всего один раствор, а потому представляют собой цепи без переноса. В этих цепях на электроде с большей концентрацией амальгамы или с большим давлением газа происходит ионизация атомов амальгамы или газа, а на электроде с меньшей концентрацией амальгамы (с меньшим давлением газа) идут обратные процессы образования амальгамы или газа. Таким образом, в результате работы концентрационной цепи происходит выравнивание активностей компонентов на обоих электродах. В качестве примера можно рассмотреть следующую амальгамную цепь:
Pt│Zn (Hg)│ZnSO4│Zn (Hg)│Pt
a1 a2
На обеих границах раздела металл – раствор идут процессы
Zn2++2e-(Hg)=Zn (Hg)
Условие равновесия на левом электроде
(1.2.11)
или
(1.2.12)
откуда
(1.2.13)
Из аналогичного равновесия на правом электроде получаем
(1.2.14)
На границах платины с амальгамами наблюдаются равновесия
e- (Pt)=e- (Ам1) и e- (Ам2)= e- (Pt)
Из условий равновесия и легко получить выражения для гальвани-потенциалов на этих двух границах:
и
электрохимический потенциал равновесие пурбе
Так как изменение состава амальгамы приводит к изменению химического потенциала электрода (т.е. ), то . Суммируя все гальвани-потенциалы в рассматриваемой цепи, получаем для ЭДС следующее простое выражение:
(1.2.15)
Рассмотрим теперь концентрационные цепи, которые содержат два раствора одинакового состава, но различной концентрации. Цепь с переносом можно построить следующим образом:
М│Мυ+ Аυ-¦ Мυ+ Аυ-│М
as(1) as(2)
где оба электрода 1-ого рода обратимы по катионам Мz+. Из условия равновесия по левой границе
или (1.2.16)
получаем для гальвани-потенциала :
(1.2.17)
Аналогично для гальвани-потенциала на правой границе имеем
(1.2.18)
Сумма этих гальвани-потенциалов равна
(1.2.19)
Чтобы получить разность потенциалов на концах цепи, к сумме гальвани-потенциалов нужно прибавить диффузионный потенциал на границе двух растворов .
Для рассматриваемой системы:
(1.2.20)
Если предположить, что концентрации двух растворов отличаются не очень сильно или оба раствора достаточно разбавлены и, следовательно, можно принять постоянство чисел переноса в переходной зоне на границе двух растворов, то из уравнения (1.2.20) находим
(1.2.21)
Складывая уравнения (1.2.19) и (1.2.21) и заменяя при этом z+=n/υ+ и │z -│=n/υ- получаем для разности потенциалов на концах цепи:
(1.2.22)
где - активность соли; - средняя активность.
При работе цепи, когда >, Е>0, следовательно, на правом электроде идет катодный процесс выделения металла. Если через цепь прошел 1 фарадей электричества, то за счет электролиза из правого раствора будет удален 1 г-экв катионов. Но через границу двух растворов в правую часть цепи перейдет t+ г-экв катионов, так что суммарная убыль катионов из правого раствора составит 1– t+= t- г-экв. Одновременно из правого раствора в левый перейдет t- г-экв анионов. Таким образом, прохождение через цепь 1 фарадея сопровождается убылью t- г-экв соли из правого раствора. Аналогичный анализ процессов в левой части цепи показывает, что при прохождении через цепь 1 фарадея здесь возникает t- г-экв соли. Следовательно, работа концентрационной цепи с переносом сопровождается выравниванием концентраций в обоих растворах. Данный вывод оказывается справедливым и при условии <, но при этом все процессы в цепи протекают в обратном направлении.
В химических цепях источником электрической энергии является свободная энергия химической реакции, протекающей в электрохимической системе.
В химических цепях без переноса один из электродов должен быть обратимым по катиону, а другой – по аниону.
Примеры:
амальгамный электрод – электрод 2-ого рода:
Ag│K(Hg)│KCl│AgCl, Ag
газовый электрод – электрод 2-ого рода:
обратимый по катионам
Pt, H2│HCl│Hg2Cl2, Hg│Pt
обратимый по анионам
Pt, H2│HCl│Cl2, Pt
электрод 1-ого рода – газовый электрод:
Zn│ZnCl2│Cl2, Pt│Zn
Среди различных химических цепей без переноса большое значение имеет цепь
Pt│Cd(Hg)│CdSO4 (насыщенный раствор)│Hg2SO4, Hg│Pt
лежащая в основе стандартного элемента Вестона. ЭДС этого элемента отличается большой стабильностью и малым температурным коэффициентом, а потому он используется в качестве стандарта при потенциометрических измерениях.
Однако подавляющее большинство химических цепей – это цепи с переносом, в которых растворы соединены или непосредственно, или через солевой мостик. Комбинируя различные окислительно-восстановительные полуреакции, можно построить очень большое число химических цепей. Разность соответствующих стандартных потенциалов позволяет в первом приближении оценить ЭДС этих цепей. Точное значение разности потенциалов на концах химической цепи в переносом рассчитать не удается, во-первых, из-за невозможности точного определения диффузионного потенциала и, во-вторых, из-за неизбежной замены активностей отдельных ионов в формуле Нернста средними активностями или прсото концентрациями этих ионов.
Пример химической цепи с переносом: элемент Даниэля – Якоби:
Cu│Zn│ZnSO4¦CuSO4│Cu
Разность потенциалов на концах этой цепи равна
(1.2.23)
1.3 Равновесные диаграммы потенциал-pH (диаграммы Пурбе или диаграммы электрохимического равновесия). Принципы построения. Использование диаграмм Пурбе
Одним из наиболее значительных достижений электрохимии 60-х годов является построение диаграмм pH-потенциал для всех важных металлов, названных в честь автора диаграммами Пурбе.
Диаграммы характеризуют, прежде всего, состав водного раствора и термодинамическую устойчивость твердой фазы (металла, оксидов, гидрооксидов и других соединений) в зависимости от двух переменных – электродного потенциала φ и pH. Каждая диаграмма построена в предположении, что все другие переменные заданы, но изменение состава водного раствора по еще одной переменной, например по концентрации иона металла, можно отобразить семейством линий. На полных диаграммах pH-потенциал наносят семейства линий при активностях ионов в растворе, равных 100, 10-2, 10-4, 10-6М. Эти линии обозначают соответственно числами 0, -2, -4 и -6. Для характеристики коррозионных процессов используют упрощенные диаграммы Ph=-потенциал. Для этого или объединяют кривые, соответствующие разным активностям ионов в водном растворе, проводя усредненную кривую, или строят диаграмму только при =10-6М.
Для расчета и построения диаграмм pH-потенциал необходимо располагать сведениями о химических и электрохимических реакциях, возможных в данной системе, об их количественных термодинамических характеристиках (энергиях Гиббса, стандартных электродных потенциалах, их температурных коэффициентах).
В области низких температур (0 – 100°С) энергию Гиббса реакции достаточно рассчитывать в приближении Улига:
(1.3.1)
Величину стандартного электродного потенциала можно определить по уравнению
(1.3.2)
В справочной литературе стандартные потенциалы отнесены к температуре 298К, их величины при других температурах могут быть найдены из уравнения (1.3.2) или по соответствующим изотермическим температурным коэффициентам. Первый изотермический коэффициент отражает изменение стандартной энтропии электродной реакции:
(1.3.3)
а второй – изменение изобарных теплоемкостей
(1.3.4)
Если известны температурные коэффициенты, то стандартный потенциал любого электрода по температуре, отличной от 298К, можно рассчитать по уравнению
(1.3.5)
Приближение Улига (=0) соответствует уравнению (1.3.5) с учетом лишь первого температурного коэффициента.
Линии на диаграммах pH-потенциал рассчитывают по равновесию, представленному в общем виде:
(1.3.6)
для которого можно записать уравнение равновесного потенциала
(1.3.7)
Где - активности компонентов в конденсированных фазах. Если один из реагентов или продуктов реакции (1.3.6) находится в газовой фазе, то вместо термодинамической активности в уравнение (1.3.7) подставляется соответствующее парциальное давление (летучесть). Вводя общепринятое обозначение ,получим
(1.3.8)
Для того, чтобы по уравнению (1.3.8) построить линию на диаграмме pH-потенциал, из условий равновесия устанавливают значения и так, чтобы последний член имел определенную величину. Затем строят прямую линию с ординатой при pH=0 и наклоном . При 298К значение равно 0,0591 В, тогда наклон составит .
Наклонные линии (m≠0, n≠0) отображают равновесия, в которых участвуют ионы H+ или OH- совместно с электронами; горизонтальные линии (m=0, n≠0) – равновесия, в которых участвуют электроны, но не принимают участия ионы H+ и OH-; вертикальные линии (m≠0, n=0) – равновесия, в которых принимают участие ионы H+ и OH-, но не участвуют электроны. Последнее равновесие является химическим, поэтому не может быть рассчитано по формуле (1.3.7). Вместо него применяют
(1.3.9)
Затем определяют pH для вертикальной линии:
(1.3.10)
М. Пурбе описал пять основных приложений равновесных диаграмм pH-потенциал чистых металлов:
1) теоретическое обоснование областей или условий коррозии (самопроизвольного растворения), иммунности (термодинамической устойчивости) и пассивации (условий, при которых термодинамически неустойчивые металлы практически не подвергаются растворению вследствие кинетических затруднений);
2) оценка стойкости металлов в воде;
3) установление металлов, которые находятся в активном или пассивном состоянии в определенной коррозионной среде;
4) оценка возможностей использования окисляющих ингибиторов коррозии (хроматов, молибдатов и т.д.);
5) классификация металлов по степени их благородности (термодинамической устойчивости) [3].
Вследствие диссоциации воды в водных растворах всегда присутствуют ионы водорода и гидроксила. Поэтому на всех электродах может протекать не только собственно электродная реакция, но и реакции, проходящие на водородном и кислородном электродах. Таким образом, теоретически в водных растворах электроды всегда рассматриваются как смешанные.
Диаграмма равновесия воды.
На простейшей, но, как указано выше, очень важной в практическом отношении диаграмме равновесия потенциалы электродных реакций, протекающих на водородном [εР(Н+/H2)] и кислородном [εР(О2/ОН-)] электродах, приведены в и зависимости от рН раствора. Эта диаграмма, кроме того, дает сведения об электрохимической устойчивости воды.
Потенциал реакции водородного электрода при 25°С можно представить в виде
(1.3.11)
учитывая, что -lg = pH. В этом уравнении =/, где - давление газообразного водорода в системе, а - давление газа, выбранное в качестве стандартной величины (1,01325·105 Па).
На кислородном электроде реализуется следующая реакция:
O2 + 2H2O + 4ē = 4OH- (1.3.12)
Потенциал электродной реакции равен
(1.3.13)
где (– давление газообразного кислорода в системе); εР (O2/OH-) – стандартный потенциал электродной реакции (1.3.12), равный 0,401 В при 25°С.
С учетом ионного произведения воды получаем выражение
(1.3.14)
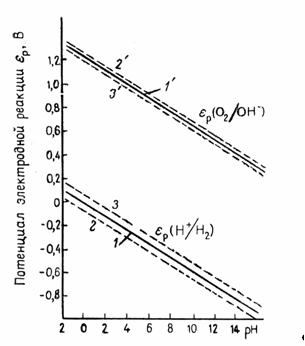
Рис. 1.3.1 - Диаграмма равновесия воды
На рис. 1.3.1. величины и , рассчитанные по уравнениям (1.3.11) и (1.3.14), приведены как функции pH. Сплошные прямые отвечают . При уменьшении pH на единицу потенциалы обоих электродов уменьшаются на 0,0591 В. Штриховые линии получают при уменьшении и увеличении давления водорода и кислорода на два порядка. В этом случае потенциал реакции водородного электрода (при постоянном pH) изменяется на 0,0591 В, а потенциал кислородного электрода – на 0,0295В. Следовательно, если построить график зависимости величин и от pH, то получаются две параллельные прямые, причем их истинное расположение зависит от давления газа. В интервале между двумя прямыми вода устойчива, т.е. при обычных условиях на электродах, работающих при потенциалах в пределах указанного интервала, не происходит выделения водорода или кислорода (это «интервал устойчивости» воды). За пределами этого интервала (т.е. при электродных потенциалах более отрицательных, чем , и более положительных, чем ) вода разлагается соответственно с выделением водорода и кислорода.
Поэтому в водных растворах можно достаточно надежно изучать равновесие и электродную реакцию на простых электродах, если потенциал данной реакции находится в пределах интервала устойчивости воды, а электролит не содержит растворенных газов H2 и O2. Если потенциал электродной реакции находится за пределами интервала устойчивости воды, то нельзя достичь равновесия исследуемой реакции [4].
1.4 Механизм и скорость электродной реакции. Равновесный и стационарный потенциалы. Ток обмена. Простые и смешанные электроды. Поляризация и перенапряжение. Их типы
Скорость электродных процессов следует рассматривать, используя общие закономерности обычных гетерогенных химических реакций, совершающихся на поверхности раздела твердой и жидкой фаз.
Назовем электродным процессом сумму всех изменений, происходящих во времени на поверхности электрода при потенциале, отличном от равновесного. Легко видеть, что электродный процесс, являясь процессом сложным, может быть расчленен на несколько стадий.
Из химической кинетики известно, что скорость наиболее медленной стадии оказывает решающее влияние на скорость процесса в целом. Если взять в пример двустадийный процесс (стадия 1 – диффузия иона из раствора к границе двойного слоя и далее к поверхности электрода; стадия 2 – электродная реакция, в которой участвуют ионы плотной части двойного слоя), то в стационарном состоянии обе стадии процесса будут протекать с одинаковой скоростью. При этом одна из них (в данном примере диффузия) имеет наибольшую возможную в данных условиях скорость; скорость второй стадии снижена недостатком реагирующего вещества, т.е. очень низкой концентрацией его у наружной границы двойного слоя.
В случае медленной электродной реакции и быстрой диффузии скорость последней оказывается снижена, так как медленный расход реагирующего вещества не создает достаточно большой разности концентраций, необходимой для развития диффузии.
В зависимости от того, какая из стадий является более медленной, можно различать электрохимическую или диффузионную кинетику электрохимического процесса.
Скорость диффузии зависит от температуры, от природы растворенного вещества и растворителя и от движения раствора, омывающего электрод. Чтобы избавиться от случайных причин, влияющих на скорость диффузии, и сделать ее постоянной, часто ведут исследование кинетики при перемешивании раствора с постоянной скоростью. Меняя скорость перемешивания раствора, т.е. скорость диффузии, иногда можно один и тот же процесс перевести из области диффузионной кинетики в область электрохимическую, и наоборот.
Рассмотрим электрохимическую кинетику, предполагая, что диффузия может протекать значительно быстрее, чем электродная реакция. Данного условия можно добиться за счет достаточно быстрого перемешивания раствора.
Для примера рассмотрим скорость электрохимической реакции, происходящей на металлическом электроде, погруженном в раствор его собственной соли.
При равновесном потенциале не прекращается протекание реакций окисления и восстановления. Ионы металла переходят с поверхности электрода в раствор и из раствора возвращаются на поверхность электрода. Но скорости этих двух противоположных процессов равны. При этом не происходит макроскопических изменений состава и массы отдельных фаз системы. Протекание процесса, приводящего к макроскопическим изменениям, возможно лишь при потенциале, отличном от равновесного, когда скорости окисления и восстановления не равны друг другу. Разность этих скоростей и будет общей скоростью процесса, которая тем больше, чем больше смещен потенциал от равновесного значения [5].
При установлении равновесия состав фаз, образующихся на электродах, остается неизменным во времени. Однако такое равновесие является динамическим, т.е. абсолютные значения анодного () и катодного () плотностей тока равны и представляют собой ток обмена . Измеряемый при этом электродный потенциал соответствует равновесному потенциалу (). В случае простых электродов условие равновесия можно представить в виде
(1.4.1)
Однако очень часто на металле, погруженном в раствор электролита, протекает несколько самопроизвольных электродных реакций, т.е. речь идет о смешанном электроде. В таких случаях на электроде устанавливается более или менее постоянный во времени компромиссный потенциал (равновесный и компромиссный потенциалы часто называют стационарным потенциалом, указывая тем самым на отсутствие тока от внешнего источника). В этом случае суммы катодных и анодных токов отдельных реакций (т.е. скорости этих реакций) также равны друг другу:
(1.4.2)
где n>1.
Равенство (1.4.2) может быть выполнено при условии, что 1) или 2) .
При условии 1 состав образующихся на электроде фаз меняется во времени, т.е. в системе отсутствует равновесие. При условии 2 на смешанном электроде устанавливается равновесие.
Для того чтобы скорости анодных и катодных процессов на электроде различались, необходимо изменить значение стационарного потенциала. При таком изменении через электрод начинает протекать электрический ток. Это можно сделать, замкнув каким-либо проводником два электрода гальванического элемента или включив исследуемый электрод в соответствующую цепь с помощью вспомогательного электрода. При этом стационарный потенциал электрода начинает изменяться под действием электрического тока. Такое явление называется поляризацией.
Разность между электродным потенциалом поляризованного электрода () и равновесным потенциалом () называется перенапряжением :
(1.4.3)
Отсюда перенапряжение – это разность между потенциалом электрода и равновесным потенциалом, необходимая для протекания заданного тока через электрод. Когда рассматривают смешанный электрод, стационарный потенциал которого не совпадает с равновесным, разность между потенциалом поляризованного электрода и компромиссным потенциалом () называют потенциалом поляризации электрода:
(1.4.4)
Если процесс окисления является единственной или преобладающей электродной реакцией на поляризованном электроде, то электрод называют анодом, а соответствующую поляризацию – анодной. Если же единственной или преобладающей реакцией является процесс восстановления, то электрод считается катодом, а поляризация называется катодной. В первом случае и положительны, во втором – отрицательны.
В соответствии с выдвинутыми ранее положениями, когда и не равны нулю, анодная и катодная плотности тока ( и соответственно) также неодинаковы и суммарная плотность тока , протекающего через электрод, будет равна
(1.4.5)
где - положительная, а - отрицательная величина.
Поляризация, как правило, бывает обусловлена затруднением («замедленностью») одной из последовательных стадий электродного процесса. Некоторые стадии представляют собой физические процессы (диффузия, образование новой фазы), а другие являются химическими или электрохимическими реакциями (например, стадия переноса заряда).
Основываясь на характере лимитирующей стадии процесса, обычно выделяют следующие типы поляризации и перенапряжения.
Диффузионное перенапряжение (концентрационная или диффузионная поляризация) возникает в том случае, когда затрудненной оказывается диффузия к электроду участвующего в электродной реакции исходного вещества (веществ) или диффузия продукта (продуктов) электродной реакции от электрода в объем раствора. Вследствие медленной диффузии при протекании тока происходит обеднение приэлектродного слоя исходными компонентами, а концентрация продуктов возрастает в сравнении с объемной (т.е. в отсутствие тока) концентрацией. Поскольку диффузия всегда участвует в электродных процессах, часто возникает и диффузионная поляризация. В таких случаях кинетика суммарного электродного процесса определяется законами диффузии (диффузионной кинетикой, диффузионным режимом).
Перенапряжение кристаллизации (кристаллизационная поляризация) также по существу обусловлено диффузионными затруднениями. Это явление возникает в том случае, когда продуктом электродной реакции является металл, а его ион не может встроиться в кристаллическую решетку металла, превратившись в соответствующий атом. Следовательно, ион металла вынужден мигрировать до места, энергетически выгодного для встраивания в решетку. При этом кристаллизация оказывается наиболее затрудненным процессом.
Перенапряжение образования центров кристаллизации, или зародышей (поляризация зародышеобразования), как правило, возникает в начальный момент пропускания тока, поскольку для образования новой фазы необходимо затратить некоторую избыточную энергию. Новая фаза образуется при осаждении металла (сплава) на электрод из другого материала или, например, при электролитическом выделении ртути или газа. В последних двух случаях, когда ртуть не смачивает электрод или когда выделяется газ, зародыши должны формироваться непрерывно: в этих условиях перенапряжение образования зародышей существует только в начальный момент пропускания тока. При выделении металла на электроде в микрокристаллическом или аморфном состоянии перенапряжение образования зародышей новой фазы может быть постоянным.
Перенапряжение переноса заряда (поляризация переноса заряда) наблюдают в том случае, когда лимитирующей стадией оказывается перенос заряда, т.е. электрохимическая реакция. При этом перенапряжение переноса можно рассматривать как разность электрических потенциалов, уменьшающую энергию активации переноса заряда до такой степени, что этот процесс становится возможным при заданной плотности тока. Поэтому такой вид поляризации часто называют активационной поляризацией.
Перенапряжение реакции (поляризация реакции) обнаруживают в том случае, когда в электродную реакцию кроме электрохимических стадий (перенос заряда) последовательно включается замедленная химическая реакция (реакции). Если последняя протекает до электрохимической стадии, то при пропускании тока концентрации участвующих в электрохимической стадии исходных компонентов окажутся ниже их равновесных значений. Если замедленная химическая реакция протекает после электрохимической стадии, то последнюю можно считать равновесной. Необходимо указать, что сложные электродные реакции состоят из нескольких стадий, среди которых может быть ряд химических и электрохимических.
Диффузионную поляризацию и поляризацию реакции часто объединяют под общим названием «концентрационная поляризация», поскольку появление этих типов поляризации сопровождается изменением концентрации участвующих в электрохимической реакции частиц относительно их равновесных концентраций. Однако электрохимическую стадию можно считать по-прежнему равновесной, но уже с изменившимися концентрациями.
Все упомянутые выше типы перенапряжения обусловлены наличием в электродном процессе лимитирующей стадии. В литературе еще имеется термин «омическое перенапряжение». Последнее, как правило, связано с измерением электродного потенциала относительно электрода сравнения с помощью солевого мостика. При протекании тока в слое жидкого электролита (или в другом поверхностном слое) между концом солевого мостика и поверхностью электрода происходит омическое падение потенциала, которое складывается с измеренным значением электродного потенциала. Таким образом, омическое перенапряжение обусловлено просто ошибкой при измерении. Эту ошибку можно уменьшить, выполнив мостик в виде капилляра, конец которого вплотную подходит к исследуемому электроду (так называемый капилляр Луггина). При этом также возможно искажение величины электродного потенциала вследствие экранирования доли поверхности электрода концом капилляра. Во избежание омического перенапряжения (когда оно весьма вероятно, например, в случае раствором с высоким сопротивлением или при образовании поверхностного слоя) в электрохимических измерениях используют потенциостаты с компенсацией омического падения напряжения.
Кинетика процесса растворения металла обычно определяется диффузионной, электрохимической и химической стадиями реакции и соответствующими типами поляризации. На практике на кинетику электродных процессов может оказывать влияние одновременно каждая из этих стадий реакции [4].
1.5 Зависимость скорости электрохимической реакции от потенциала. Поляризационные кривые
Скорость химической реакции изменяется с изменением потенциала. Сдвиг потенциала от равновесного значения, определяя скорость реакции, должен, очевидно, влиять на величину энергии активации. В этом заключается важнейшая особенность электродных реакций по сравнению с обычными химическими. Изменение потенциала, которое мы можем в известных пределах осуществлять по своему желанию, вызывает изменение энергии активации, т.е. изменяет и скорость процесса.
Удельную скорость электродной реакции удобно выражать через плотность тока. Для реакций окисления и восстановления на электродах можно записать следующие уравнения:
(1.5.1)
где - энергия активации.
Если мы найдем связь между энергией активации или и сдвигом потенциала от равновесного значения , то с помощью уравнения (1.5.1) можно определить зависимость между скоростями реакций или и .
Величина работы А перехода 1 г-иона металла в раствор измеряется разностью потенциальной энергии катионов на поверхности электрода и сольватированных катионов в плотной части двойного слоя, находящихся на расстоянии от поверхности электрода. В плотной части двойного слоя осуществляется скачок потенциала . Выражая величину А в электрических единицах, получим
(1.5.2)
Величина зависит от природы металла и концентрации ионов в двойном слое. Очевидно, что изменить потенциал металла можно, изменив строение двойного слоя, в частности, увеличив или уменьшив концентрацию ионов у поверхности электрода. Этого можно в известной мере добиться просто изменением концентрации раствора. Однако в данном случае такой вариант не подходит, так как новой концентрации будет отвечать новый равновесный потенциал, и реакции окисления протекать не будет. Также потенциал можно изменить и за счет приложения ЭДС от внешнего источника, причем через поверхность электрода протекает ток. Для этого должен быть использован вспомогательный электрод, и от какого-либо источника ЭДС между электродами должен быть пропущен ток. В зависимости от направления тока потенциал рассматриваемого электрода может быть сдвинут в сторону более положительных или более отрицательных значений от равновесного [5].
Измеряемый катодный ток определяется разность токов прямого и обратного направления:
(1.5.3)
Поскольку ток обмена является частным значением токов или при , уравнение (1.5.3) можно преобразовать к виду
(1.5.4)
Так как функциональные зависимости и имеют вид и , то уравнение (1.5.4) можно записать в форме
(1.5.5)
Где - катодное перенапряжение стадии разряда – ионизации.
Уравнение (1.5.5) в сочетании с выражением для тока обмена является общим уравнением поляризационной кривой для одностадийной реакции разряда – ионизации. Проанализируем уравнение (1.5.5), предполагая, что , а - потенциал достаточно мал для того, чтобы можно было пренебречь зависимостью от . При выполнении условия, что намного превышает значение можно пренебречь второй экспонентой в уравнении (1.5.5), так что
(1.5.6)
или
(1.5.7)
Вводя обозначения и , уравнение (1.5.7) можно переписать в виде
(1.5.8)
Уравнение (1.5.8) называют уравнением Тафеля. По наклону тафелевской прямой легко найти коэффициент переноса , а затем, учитывая связь константы с , определить ток обмена.
При больших анодных перенапряжениях, когда и намного превышает значение , из уравнения (1.5.5) следует
(1.5.9)
или
(1.5.10)
Уравнение (1.5.10) также имеет вид уравнения Тафеля.
В области малых перенапряжений, где намного меньше значения , можно разложить экспоненты в уравнении (1.5.5) и ограничиться первыми двумя членами разложения:
(1.5.11)
откуда
(1.5.12)
Таким образом, вблизи равновесного потенциала должна наблюдаться линейная зависимость между и .
Из соотношения (1.5.12) видно, что чем больше ток обмена, тем меньше отклонение потенциала от его равновесного значения при данной плотности тока и наоборот. На основе уравнения (1.5.12) можно дать более строгое определение понятиям идеально поляризуемого и идеально неполяризуемого электродов. Так, идеально поляризуемый электрод – это такой электрод, плотность тока обмена на котором равна нулю: . Если бы не было двойного слоя, любой сколь угодно малый ток вызвал бы бесконечно большое смещение потенциала. Идеально неполяризуемый электрод – это электрод, которому отвечает бесконечно большой ток обмена: . Реальный ток обмена всегда имеет некоторую конечную величину. Но если оказывается значительно больше протекающего через электрод тока , то согласно уравнению (1.5.12) изменением потенциала этого электрода можно пренебречь. Так как при условии, что , сдвиг потенциала электрода не должен превышать 2,5 мкВ. Поэтому в качестве электродов сравнения обычно выбирают электрохимические системы с достаточно большими токами обмена. Если , то уравнение (1.5.5) преобразуется:
(1.5.13)
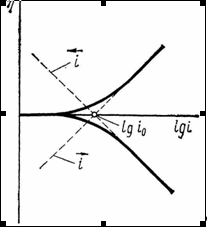
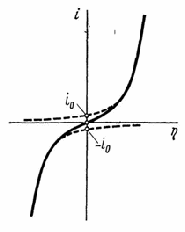
Рассчитанная по (1.5.13) кривая симметричная относительно начала координат (рис. 1.5.1). При отклонениях от 0,5 нарушается симметричность -кривой. Пунктиром на рис. 1.5.1 показаны поляризационные кривые, отвечающие зависимостям и . При .
Рис. 1.5.1 - Поляризационная кривая стадии разряда – ионизации при и
Поскольку в широком интервале потенциалов зависимость тока от перенапряжения носит экспоненциальный характер, обычно поляризационную кривую изображают в полулогарифмических координатах (рис. 1.5.2). Экстраполяция прямолинейных участков кривых для катодного и анодного перенапряжения до позволяет рассчитать ток обмена .
Рис. 1.5.2 - Поляризационная кривая стадии разряда – ионизации при и в полулогарифмических координатах
На практике редко встречаются простые электрохимические системы, для которых кинетические закономерности стадии разряда – ионизации можно было бы экспериментально изучить как вблизи равновесного потенциала, так и при значительном удалении от равновесного состояния. Это связано с различной зависимостью от потенциала диффузионной стадии электродного процесса и стадии разряда – ионизации. С одной стороны, после достижения предельного диффузионного тока скорость диффузионной стадии не зависит от потенциала. С другой стороны, по мере удаления от равновесного потенциала скорость стадии разряда – ионизации очень резко возрастает [7].
1.6 Поляризационные диаграммы потенциал – pH
Теория коррозии – это не рядовое приложение кинетики и термодинамики электродных реакций, а одно из самых сложных направлений электрохимии. В настоящее время рождается новый метод исследования коррозии с помощью поляризационных диаграмм потенциал – pH.
Экспериментальное определение координат поляризационной диаграммы потенциал – pH можно осуществить, используя методику Марселя Пурбе.
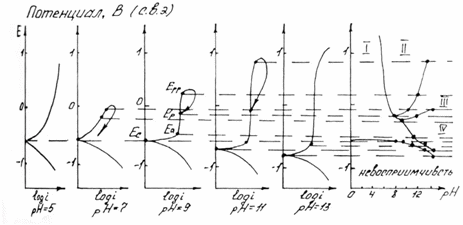
Рис. 1.6.1 - Метод построение экспериментальных диаграмм потенциал – pH: I – общая коррозия, II – питтинговая коррозия, III – неустойчивая пассивность, IV – пассивность
На рис. 1.6.1. схематически показаны пять потенциодинамических поляризационных кривых для железа в растворе хлорида при pH 5, 7, 9, 11 и 13 соответственно. Совмещением особых точек этих кривых справа можно получить поляризационную диаграмму железа, на которой отображены экспериментальные условия иммунности (невосприимчивости), общей коррозии, питтинговой коррозии, пассивности и неустойчивой пассивности, как функцию потенциала и pH. Потенциал, разделяющий области невосприимчивости и общей коррозии, - стационарный или коррозионный (Ec) потенциал. Потенциал, разделяющий область общей коррозии и пассивности, - потенциал пассивации (Ea). При потенциалах положительнее Ea на металле образуется защитная пленка окислов. Потенциал Epp (потенциал питтингообразования) – потенциал, выше которого металл подвергается питтинговой коррозии. При питтинге наблюдается очень быстрое активное растворение металла на определенных участках его поверхности (в коррозионных язвах, или питтингах), в то время как другие участки поверхности металла остаются в пассивном состоянии. Ep – критический защитный потенциал (потенциал репассивации питтингов). При потенциалах отрицательнее Ep уже имеющиеся питтинги не будут расти дальше и поврежденная пассивационная пленка будет восстановлена. Линия, отвечающая потенциалам репассивации питтингов Ep, разделяет область пассивности на две части: верхнюю – область неустойчивой пассивности, в которой уже имеющиеся язвы продолжают расти, и нижняя- полной (устойчивой) пассивности, в которой ранее образовавшиеся питтинги восстанавливают свою пассивность.
Поляризационная диаграмма потенциал – pH реагирует на электродные потенциалы появления новых фаз и фазовые переходы на поверхности металлов, указывая границы начала и конца фазовых превращений. Поэтому поляризационные диаграммы имеют все признаки диаграммы фазового равновесия. Для идентификации фазовых превращений на поляризационных диаграммах их совмещают с соответствующими равновесными диаграммами потенциал – pH [6].
2. Расчет и построение равновесной диаграммы потенциал – pH для системы Cu – H2O
В системе Cu – H2O присутствуют Cu, Cu2+, Cu2O, CuO и Cu2O3.
Реакции окисления меди до оксидов приведены ниже:
(1) Cu0 + 0,5O2 = CuO = - 129 365 Дж/моль
(2) 2Cu0 + 0,5O2 = Cu2O = - 150 548 Дж/моль
(3) 2Cu0 + 1,5O2 = Cu2O3 = ?
Для (3) реакции:
= 100 Дж/моль·К для Cu2O3
= 33,149 Дж/моль·К для Cu
= 205,036 Дж/моль·К для O2
= - 355 000 Дж/моль·К
Отсюда по уравнению находим = - 273 392 Дж/моль
(4) Cu2O + 0,5O2 = 2CuO = ?
(5) 2CuO + 0,5O2 = Cu2O3 = ?
Для (4) и (5) реакций по закону Гесса находим:
= 2· - = - 106 182 Дж/моль
= - 2· = - 14 662 Дж/моль
Для некоторого процесса энергию Гиббса можно рассчитать как:
(2.1)
Здесь - это минимальное значение давления кислорода в газовой фазе, при котором в среде начнется окисление. Соответственно, чем меньше , тем легче окисление Me.
Исходя из уравнения (2.1) найдем значения для реакций (1), (3) и (4):
= 4,57·10-46 атм.
= 1,18·10-38 атм.
= 7,28·10-6 атм.
В системе может протекать выделение кислорода:
(6) O2 + 4ē + 4H+ = 2H2O = - 470 461 Дж/моль
Фазовые переходы Cu в данной системе описываются следующими уравнениями:
(I) Cu2+ + 2ē = Cu0 φ = 0,337 B = - 65 031 Дж/моль
(II) Cu2O + 2H+ + 2ē = 2Cu0 + H2O φ = ? = - 84 682 Дж/моль
(III) 2Cu2+ + H2O + 2ē = Cu2O + 2H+ φ = ?
(IV) 2CuO + 2H+ + 2ē = Cu2O + H2O φ = ?
(V) CuO + 2H+ = Cu2+ + H2O φ = ?
(VI) Cu2O3 + 6H+ + 2ē = 3H2O + 2Cu2+ φ = ?
(VII) Cu2O3 + 2H+ + 2ē = 2CuO + H2O φ = ?
По закону Гесса для реакций (III) – (VII):
= 2· - = - 45 380 Дж/моль
= + 0,5· - 2· = -127 049 Дж/моль
= 0,5· - - = - 40 835 Дж/моль
= 1,5· - 2· - = - 302 238 Дж/моль
= 0,5· + 2· - = - 220 569 Дж/моль
В общем виде электродный процесс можно записать как:
По основному закону термодинамики электрохимических систем:
(2.2)
Свободная энергия Гиббса определяется по следующей формуле:
Δ (2.3)
Подставляя (2.3) в (2.4), переходя от натуральных логарифмов к десятичным и с учетом того, что , получаем:
(2.4)
Для линий чисто химических равновесий энергия Гиббса вычисляется по формуле:
(2.5)
Подставляя уравнение (2.5) в (2.2) и проводя соответствующие преобразования, получаем:
(2.6)
Исходя из приведенных выше формул, ведется расчет линий зависимости φ от pH для реакций (I) – (VII):
№ линии
Электродная реакция
Равновесный потенциал, В (н. в. э.) или рН раствора
I
II
III
IV
V
VI
VII
Для линий I, III, V и VI величину активности ионов Cu2+ можно варьировать. В данном случае берутся значения = 0, 10-2, 10-4 и 10-6. Тогда:
Для I:
φ1 = 0,337 В
φ2 = 0,278 В
φ3 = 0,219 В
φ4 = 0,160 В
Для III:
φ1 = 0,235 + 0,0591pH
φ2 = 0,117 + 0,0591pH
φ3 = - 0,001 + 0,0591pH
φ4 = - 0,120 + 0,0591pH
Для V:
pH1 = 3,58
pH2 = 4,58
pH3 = 5,58
pH4 = 6,58
Для VI:
φ1 = 1,566 – 0,1773pH
φ2 = 1,684 – 0,1773pH
φ3 = 1,802 – 0,1773pH
φ4 = 1,921 – 0,1773pH
Для данной системы построена равновесная диаграмма потенциал – pH:
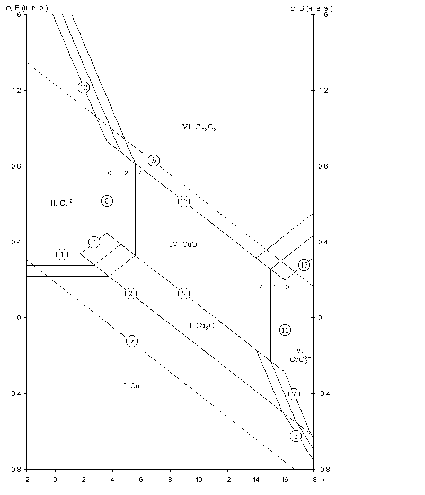
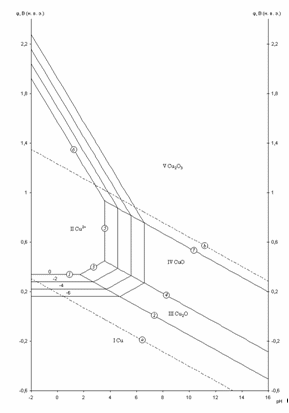
Рис. 2.1 - Равновесная диаграмма потенциал – pH для системы Cu – H2O
На диаграмме можно выделить 5 областей преобладания фаз различного состава. Область I – область иммунности меди, при данных значениях потенциалов и рН медь коррозии не подвергается. Область II – область активной коррозии, в которой медь переходит в раствор в виде катионов Cu2+. Области III, IV – области пассивации, на поверхности меди образуется защитная пассивирующая плёнка, состоящая из оксида Cu2O (область III) и CuO (область IV) Область V – область перепассивации. Линии a и b на диаграмме определяют область электрохимической устойчивости воды.
Данная диаграмма построена без учета существования Cu в данной системе в виде анионов.
Ниже приведены дополняющие картину системы уравнений реакций:
(VIII) HCuO2- + H+ = CuO + H2O pH = 18,83 + lg
(IX) Cu2O3 +H2O + 2ē = 2HCuO2- φ = ?
(X) 2HCuO2- + 4H+ + 2ē = Cu2O +3H2O φ = 1,783 – 0,1182pH + 0,0591·lg
(XI) CuO22- + H+ = HCuO2- pH = 13,15 + lg
(XII) 2CuO22- + 6H+ + 2ē = Cu2O + 3H2O φ = 2,560 – 0,1773pH + 0,0591·lg
(XIII) Cu2O3 + H2O + 2ē = 2CuO22- + 2H+ φ = ?
(XIV) CuO22- + 4H+ + 2ē = Cu + 2H2O φ = 1,515 – 0,1182pH + 0,0295·lg
Аналогично расчетам для уравнений реакций (I) – (VII) для реакций (IX) и (XIII) получаем:
φ(IX) = 0,0309 –0,0591·lg
φ(XIII) = –0,759 + 0,0591pH + 0,0591·lg
Для системы Cu – H2O построена дополненная диаграмма потенциал – pH:
Рис. 2.2 - Равновесная диаграмма потенциал – pH для системы Cu – H2O с учетом существования Cu в виде анионов
На данной диаграмме показаны все условия перехода меди из одних состояний в другие. Можно заметить, что в очень кислой среде пассивирующая пленка меди разрешается, вследствие чего медь вновь переходит в раствор, но на этот раз уже в виде анионов HCuO2- и CuO22-. Отсюда можно сделать вывод, что медь неустойчивак коррозии при высоких значениях pH.
Выводы
В работе изучены основные представления о электрохимических системах, рассмотрены классификация электродов и классификация самих систем.
Рассмотрены равновесные диаграммы потенциал-pH, изучены основные принципы их построения и анализа.
Изучены поляризационные кривые и поляризационные диаграммы потенциал-pH, принципы их построения, перехода от кривых к диаграммам.
В работе рассчитаны основные химические и электрохимические равновесия в системе Cu – H2O при 298 К и 1 атм. На основе этих данных построена диаграмма электрохимического равновесия данной системы.
Были проанализированы термодинамические особенности окисления меди на воздухе. Показано принципиальная возможность образования оксида Cu2O3 в стандартных условиях.
СПИСОК ЛИТЕРАТУРЫ
Герасимов Я.И. Курс физической химии [Текст] / Я.И. Герасимов, В.П. Древинг, Е.Н. Еремин, А.В. Киселев, В.П. Лебедев, Г.М. Панченков, А.И. Шлыгин // – 2-е изд., знач. доп. – М: Химия, 1973. Т. 2 – 624 с.
Дамаскин Б.Б. Электрохимия: учебное пособие для хим. фак. ун-тов [Текст] / Б.Б. Дамаскин, О.А. Петрий // М: Высшая школа, 1987. – 295 с.
Термодинамика химической и электрохимической устойчивости сплавов: учебное пособие [Текст] / авт.-сост. А.Г. Тюрин. Ч.I. – Челябинск: ЧелГУ, 2004.
Киш Л. Кинетика электрохимического растворения металлов [Текст] / пер. с англ. Е.В. Овсянниковой; под ред. А.М. Скундина // – М: Мир, 1990. – 272 с.
Скорчеллетти В.В. Теоретическая электрохимия. – Л: Государственное Научно-техническое издательство химической литературы, 1963. – 608 с.
Тюрин А.Г. Термодинамика химической и электрохимической устойчивости сплавов: [Текст]: дис. докт. хим. наук / Тюрин Александр Георгиевич – Челябинск: 2007.
Дамаскин Б.Б. Введение в электрохимическую кинетику: Учеб. пособие для студентов хим. спец. ун-тов [Текст] / Б.Б. Дамаскин, О.А. Петрий // – 2-е изд., перераб. и доп. – М: Высшая школа, 1983.

Нравится материал? Поддержи автора!
Ещё документы из категории химия:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ