Введение

Целью курсового проекта по дисциплине «Аналоговые и гибридные ЭВМ» является закрепление основных теоретических знаний и практических навыков в ходе самостоятельной работы.

Методы аналоговой вычислительной техники вместе с методами цифровой вычислительной техники занимают важное место в современной науке и технике. Исследование физических процессов и сложных динамических систем, которые описываются системами дифференциальных уравнений высокого порядка с большим количеством нелинейностей, наиболее целесообразно проводить при помощи АВМ. Это объясняется тем, что специфика аналоговых машин позволяет инженеру не только выполнять ряд необходимых вычислений, но и исследовать системы в условиях, максимально близких к реальным ситуациям.

В ходе работы необходимо:

1. разработать программу решения дифференциального уравнения с изменяемой правой частью.

2. обеспечить управление процессом решения и задания начальных условий при помощи цифровой ЭВМ.

1. Выбор варианта задания

35 – число, заданное преподавателем

3 – номер по списку

35+3=38 – номер варианта

Для варианта 38 заданы следующие параметры:

ny (t) Y_max NT, с ∆Uдоп, % m МП, V

5 cos t 0,5 10 1 0,2 6 ⁺ _– 10

n – порядок дифференциального уравнения

N – разрядность аналого – цифровых и цифроаналоговых преобразователей, которые задают входные величины и преобразуют результаты решения

у(t) – математическое описание нелинейной функции

Y_{max –} амплитудное значение нелинейной функции

T – период перезапуска моделирующей схемы

∆Uдоп – допустимая погрешность интегрирования

Начальные условия:

x⁴(0) х³(0) х²(0) х¹(0) х(0)

0 3 0 1 6

Максимальные значения :

x⁵_max x⁴_max х³_max х²_max х¹_max x_max

-8 -8 8 -7 -5 1

Коэффициенты:

a₄ а₃ а₂ а₁ а₀ b

2 1 -1 2 12 28

t= t(0)=0

Интервал t_y определения нелинейной функции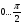

Заданное уравнение имеет вид:

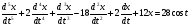
2. Выполнение программирования задачи

Заданное уравнение имеет вид:

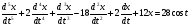
_{Заданное уравнение записываем относительно старшей производной:}

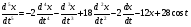
_{Построение предварительной схемы решения уравнения:}

2.1 Расчёт масштабных переменных

Масштабом произвольной переменной называется число, показывающее величину напряжения, приходящегося на единицу этой переменной. В общем случае масштаб М_х определяется выражением:

М_х = U_мп/x_max [в/ед.],

где U_мп – напряжение, действующее в машине.

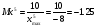
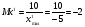
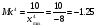
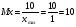
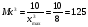
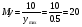
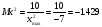
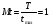
3.2 Расчёт коэффициентов передачи

Для усилителя у₁:

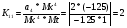
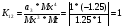
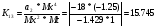
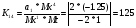
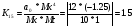
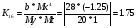
Для усилителя у₂:

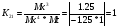
Для усилителя у₃:

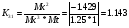
Для усилителя у₄:

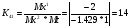
Для усилителя у₅:

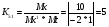
Для усилителя у₆:

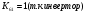
Для усилителя у₇:

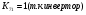
Для усилителя у₈:

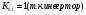
3.3 Расчёт напряжений начальных условий

Знак начальных условий определяется знаком действующей на выходе усилителя переменной. Если она имеет свой знак (+), то начальные условия подаются с заданным в задаче знаком; если переменная на выходе усилителя формируется с противоположным знаком (–), то начальные условия вводятся с обратным заданному знаком. Для ввода начальных условий в машину, их величины трансформируют с помощью масштабов в соответствующие значения напряжений, при этом получим:

U_x⁴(0) = M_x⁴ * x⁴(0) * (-1) = (-1.25)*0*(-1) = 0V

U_x³(0) = M_x³ * x³(0) * (+1) = 1.25*3*(+1) = 3.75V

U_x²(0) = M_x² * x²(0) * (-1) = -1.429*0*(-1) = 0V

U_x¹(0) = M_x¹ * x¹(0) * (+1) = -2*0*(+1) = -2V

U_x (0) = M_x * x (0) * (-1) = 10*6*(-1) = -60V – выходит за пределы МП=⁺_-10V

Новые значения напряжения начальных условий:

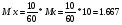
U_x (0) = M^`_x * x (0) * (-1) = 1.667*6*(-1) = -10V

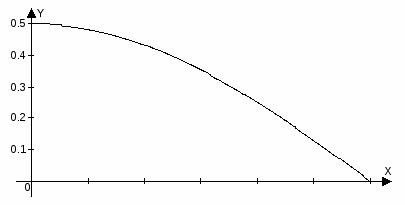
3. Аппроксимация нелинейной функции

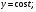
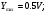
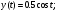
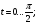
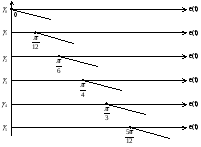
x 0 /12 /6 /4 /3 5/12 /2

y 0,5 0,483 0,433 0,354 0,25 0,129 0

Так как интервал разбиения функции равен 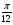_{, то вычисляем следующие коэффициенты наклона соответствующих участков аппроксимируемой функции:}

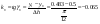
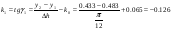
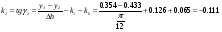
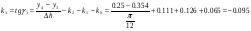
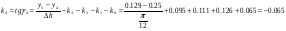
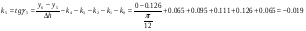14 1

1. Построение блоков формирования отрезков аппроксимирующей функции

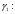
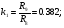
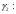
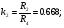
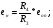
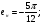
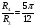
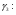
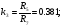
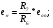
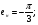
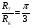
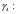
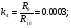
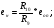
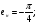
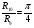
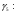
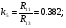
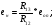
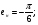
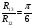
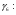
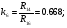
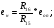
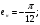
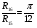
5. Формирование функции времени

_{Интервал изменения:}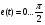

_{Время циклического перезапуска: T = 1c}

_{Теперь смоделируем функцию:}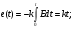

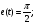
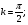
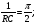
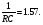
6. Аппроксимация

ША

ШД

ШК

Б1

Б2

РС

Рисунок 2.1 - Структурная схема аналого-цифрового прибора

y(t) K₁₁

- x^/ K₁₂

- x K₁₃

У₁

- x^/ K₂₁

x (0)

+x K₃₁

- x

У₂

У₃

- x^/ (0)

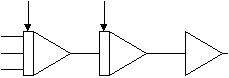
Рисунок 3.1 – Схема решения уравнения

Ф

ДБНФ

1

ДБНФ

2

ДБНФ

6

СУМ

U

t

y(t₁)

y(t₂)

y(t₆)

y(t)

Рисунок 3.2 – Блок-схема формирования нелинейной функции

Таким образом, автоматически формируется левая часть уравнения. При этом условно считается, что старшая производная x// известна, поскольку члены правой части уравнения известны и могут быть подключены к входам У1 (рисунок 3.1). Операционный усилитель У3 выполняет роль инвертора сигнала +х. Для моделирования x// необходимо в схему ввести еще один підсумовуючий усилитель, на входы которого необходимо подать сигналы, которые моделируют правую часть уравнения (3.2).

Рассчитываются масштабы всех переменных с учетом того, что максимальная величина машинной переменной за абсолютной величиной равняется 10 В:

Mx = 10 / xmax; Mx/ = 10 / x/ max; Mx// = 10 / x //max;

My = 10 / ymax. (3.3)

Масштаб времени Mt = T / tmax = 1, поскольку моделирование задачи осуществляется в реальном масштабе времени.

Рассчитываются коэффициенты передачи по каждому входу интегрирующих усилителей.

Для усилителя У1 коэффициенты передачи находятся за формулами:

K11 = Mx/ b / (MyMt); K12 = Mx/ a2 / (MxMt);

K13 = Mx/ a1 / (MxMt). (3.4)

Для усилителя У2:

K21 = Mx/ / (Mx/ Mt), (3.5)

и для усилителя У3:

К31 = 1. (3.6)

Напряжения начальных условий вычисляются за формулами:

ux/ (0) = Mx/ x/ (0) (-1); ux(0)= Mxx(0) (+1). (3.7)

Правая часть уравнения (3.2) представлена нелинейной функцией, которая задается путем линейной аппроксимации. При этом необходимо проверять, чтобы погрешность аппроксимации не превышала заданную величину. Блок-схема формирования нелинейной функции представлена на рисунку 3.2.

7. Описание принципиальной схемы

Блок формирования функции времени (Ф) выполняется в виде одного (для формирования t) или двух последовательно соединенных (для формирования t2) интегрирующих усилителей с нулевыми начальными условиями.

В этом случае при подаче на вход первого интегратора сигнала U, на его выходе получим:

u1(t)= – K11 = – K11Et. (3.8)

Положив K11E=1, имеем u1(t)= t.

На выходе второго интегратора получим:

u2(t)= K21 = K11K21Et2 / 2 (3.9)

Положив K11K21E/2 = 1, имеем u2(t)= t2.

Блоки формирования отрезков аппроксимирующей функции реализуются в виде диодных блоков нелинейных функций (ДБНФ), входной величиной для которых является функция времени t или t2. Порядок расчета и построения ДБНФ приведенные в [1, с. 59 – 69].

Сумматор (ГРУСТЬ) отрезков аппроксимирующей функции выполняется в виде дифференциального итогового усилителя.

Начальные условия для интеграторов моделирующей схемы вводятся с помощью узла с переменной структурой (рисунок 3.3). Эта схема может работать в двух режимах:

а) интегрирование – при положении ключа К в позиции 1. При этом исходный сигнал схемы с достаточной точностью описывается уравнением идеального интегратора:

u1(t)= – (1 / RC) . (3.10)

Этот режим используется при моделирование задачи. Для проверки правильности выбора параметров R и C интегратора проверяют величину исходного напряжения интегратора в функции времени и полезное время интегрирования в пределах допустимой ошибки ?Uдоп.

Величина исходного напряжения интегратора

U(t)= – KYE {1 – e – Т / [(Ky+1)RC} (3.11)

за время моделирования Т при интегрировании входного сигнала E с использованием операционного усилителя с коэффициентом передачи Ky без цепи обратной связи не должна превышать значения машинной переменной (10 В).

Время интегрирования

Tи = 2RC(Kу + 1)?Uдоп (3.12)

при выбранных параметрах схемы не должен быть меньше, чем время моделирования Т.

б) задание начальных условий реализуется при переводі ключа К в положение 2. Этот режим используется при подготовке моделирующей схемы к процессу решения. При этом исходный сигнал схемы описывается уравнением:

u0(t)= – (R2 /R1) E (3.13)

где u0(t) – величина начальных условий.

С целью сокращения времени формирования начальных условий и обеспечение надежной работы, параметры схемы должны удовлетворять условие: R1C1 = R2C.

Построить полную расчетную схему. При этом следует пользоваться условными обозначениями, приведенными в подразделе 3.1.

Пользуясь разрядностью входных и исходных данных, построить принципиальные схемы блоков Б1 и Б2 и соединить их с блоком РС.

Вывод

В ходе работы над курсовым проектом по дисциплине «Аналоговые и гибридные ЭВМ» были закреплены основные теоретические знания и практические навыки, включающие задачи анализа и синтеза формул и схем.

В результате выполнения данной работы были приобретены практические навыки при программировании задач и проектировании принципиальных схем аналого-цифровых устройств вычислительной техники. Были построены функциональная схема, которая реализует решение дифференциального уравнения, и принципиальная схема полученного входе решения устройства.

Список литературы

1. Применение интегральных микросхем в электронной вычислительной технике: Cправочник; Под ред. Б.Н. Файзулаева, Б.В. Тарабрина. – М.: Радио и связь, 1986.

2. Анисимов Б.В., Голубкин В.Н., Петраков С.В. Аналоговые и гибридные ЭВМ. – М.: Высшая школа., 1986.

3. Гутников Б.Г. Телец В.А. Интегральная электроника в измерительных устройствах. – Л.: Энергоатомиздат, 1988.

4. Федорков Б.Г. Телец В.А. Микросхемы ЦАП и АЦП: функционирование, параметры, применение. М.: Энергоатомиздат, 1988.