Задание

Разработать программу-калькулятор CalcKurs на языке программирования Pascal, реализующую следующие функции:

1. формирование заданного подмножества натурального ряда с помощью общего делителя;

2. факторизация числа с опциями;

3. нахождение НОД и НОК для заданной совокупности натурального ряда;

4. нахождение рациональных решений уравнения с целочисленными коэффициентами;

5. представление рациональной дроби в виде цепной;

6. представление цепной дроби в виде рациональной.

Оборудование и ПО:

Название Windows: Windows Seven (6.1.7600) Ultimate

Название процессора: Intel (R) Core (TM) 2 CPU 6300 @ 1.86GHz

Установлено памяти: 1 022,49 MB

Среда программирования: Turbo Pascal 7.0

Оглавление

1. Введение

Теория чисел - это одно из направлений математики, которое иногда называют "высшей арифметикой". Данная наука изучает натуральные числа и некоторые сходные с ними объекты, рассматривает различные свойства (делимость, разложимость, взаимосвязи и так далее), алгоритмы поиска чисел, а также определяет ряд достаточно интересных наборов натуральных чисел.

Так, к примеру, в рамках теории чисел рассматриваются вопросы делимости целых чисел друг на друга, алгоритм Евклида для поиска наибольшего общего делителя, поиск наименьшего общего кратного, малая и большая теоремы Ферма. В качестве самых известных рядов натуральных чисел можно привести ряд Фибоначчи, простые числа, совершенные и дружественные числа, степени и суперстепени натуральных чисел. ^[1]

Вне самой математики теория чисел имеет довольно мало приложений, и развивалась она не ради решения прикладных задач, а как искусство ради искусства, обладающее своей внутренней красотой, тонкостью и трудностью. Тем не менее теория чисел оказала большое влияние на математическую науку, поскольку некоторые разделы математики (в том числе и такие, которые впоследствии нашли применение в физике) были первоначально созданы для решения особенно сложных проблем теории чисел. ^[2]

Разработанная программа включает в себя набор из нескольких основных операций, которые могут понадобиться при решении более сложных задач.

Назначение программы CalcKurs.

Программа CalcKurs выполняет следующие функции:

1. формирование заданного подмножества натурального ряда с помощью общего делителя;

2. факторизация числа с опциями;

3. нахождение НОД и НОК для заданной совокупности натурального ряда;

4. нахождение рациональных решений уравнения с целочисленными коэффициентами;

5. представление рациональной дроби в виде цепной;

6. представление цепной дроби в виде рациональной.

2. Специальная часть

2.1 Интерфейс программы

3. Описание процедур

3.1 Procedure DelOstatok

Назначение.

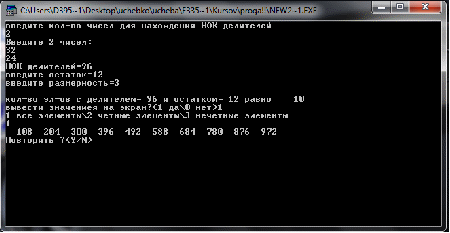
Данная процедура формирует заданное подмножество натурального ряда с помощью общего делителя.

Алгоритм.

Ищется общий делитель совокупности делителей (общий делитель ищется с помощью нахождения наименьшего общего кратного делителей). На заданном множестве (кол-во цифр в числах) ищем первый элемент, который будет удовлетворять заданному условию (делится на НОК с остатком), запоминаем элемент и прерываем цикл.

Формируем подмножество с помощью прибавления к первому элементу делителя, суммируем количество элементов, пока элементы не станут больше заданной размерности.

Пример. Делитель=10, остаток=3, размерность=2 (от 10 до 99)

Количество элементов=9. Подмножество элементов={13, 23, 33, 43, 53, 63, 73, 83, 93}. Тесты.

1. Некорректные данные

2. Корректные данные

3.2 Procedure Factor

Назначение.

Данная процедура выполняет факторизацию (разложение на простые множители) числа с опциями.

Алгоритм.

Ищем для данного числа простой множитель с помощью решета Эратосфена ^[3]

Для нахождения всех простых чисел не больше заданного числа n, следуя методу Эратосфена, нужно выполнить следующие шаги:

Выписать подряд все целые числа от двух до n (2, 3, 4, …, n).

Пусть переменная p изначально равна двум - первому простому числу.

Вычеркнуть из списка все числа от 2p до n, делящиеся на p (то есть, числа 2p, 3p, 4p, …)

Найти первое не вычеркнутое число, большее чем p, и присвоить значению переменной p это число.

Повторять шаги 3 и 4 до тех пор, пока p не станет больше, чем n

Все не вычеркнутые числа в списке - простые числа)

и делим заданное число на данный множитель, потом ищем следующий простой множитель (если он повторяется, то возводим его в степень), и так до тех пор, пока число не станет равным единице. Записываем все простые множители.

Далее находим все делители числа и составляем из них множество. Вычисляем сумму делителей.

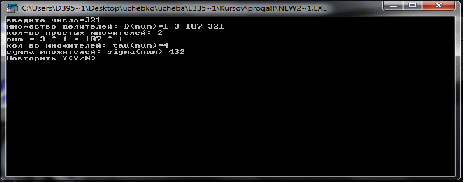
Пример.

Число=21

множество делителей=1 3 7 21, кол-во простых множителей=2

21=3 ^ 1 * 7 ^ 1

кол-во множителей=4, сумма множителей=32

Тесты.

1. Некорректные данные

2. Корректные данные

3.3 Procedure NodNok

Назначение.

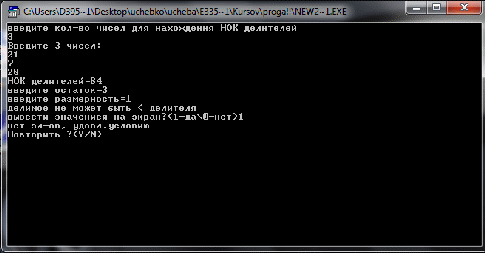
Данная процедура находит НОД и НОК для заданной совокупности натурального ряда.

Алгоритм.

С помощью алгоритма Евклида (есть числа a,b и последовательность R₁>R₂>R₃>…>R_N, где каждое R_K - это остаток от деления предпредыдущего числа на предыдущее, а предпоследнее делится на последнее нацело. Тогда НОД (a,b), наибольший общий делитель a и b, равен R_N, последнему ненулевому члену этой последовательности) находим НОД ^[4] для первых двух чисел, "цепляем" следующее число для нахождения следующего НОД, и так до тех пор, пока совокупность чисел не закончится.

Для нахождения НОК первых двух чисел используем следующий алгоритм: разлагаем данные числа на простые множители и к одному из таких разложений приписываем множители недостающие у него против разложений остальных данных чисел ^[5], и аналогично нахождению НОД "цепляем" следующее число.

Пример.

Числа: 21 и 12

НОД (12,21) =3

НОК (12,21) =84

Тесты.

1. Некорректные данные

2. Корректные данные

3.4 Procedure SuperGorner

Назначение.

Данная процедура находит рациональные решения уравнения с целочисленными коэффициентами.

Алгоритм.

Рациональные корни уравнения ищутся с помощью расширенной схемы (метода) Горнера ^{[6] (}раскладываем свободный член и коэффициент перед старшей степенью на все возможные множители и делим все множители свободного члена на все множители коэффициента перед старшей степенью (добавляем также знак “-”); подставляем полученные значения в уравнение, если уравнение получается равным нулю, то это значение - корень данного уравнения).

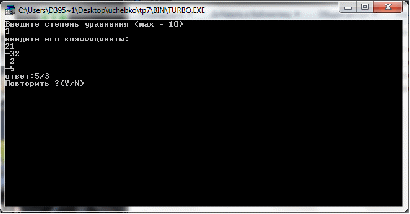
Пример. Уравнение: 6x³-11x²+6x-1=0

Возможные корни: +1, +1/2, +1/3, +1/6

Корни уравнения: 1/3, 1/2, 1

Тесты.

1. Некорректные данные

2. Корректные данные

3.5 Procedure Express

Назначение.

Данная процедура переводит рациональную дробь в цепную ^[7].

Алгоритм.

Делим числитель на знаменатель, запоминаем его целое значение (a div b, где а - числитель, b - знаменатель), находим остаток от деления числителя на знаменатель (a mod b), присваиваем числителю значение остатка, меняем местами числитель и знаменатель, и так делаем до тех пор, пока (a mod b) не станет равен нулю.

Пример.

Рациональная дробь: 123/47

Цепная дробь: [2,1,1,1,1,1,1,3]

Тесты.

1. Некорректные данные

2. Корректные данные

3.6 Procedure AntiExp

Назначение.

Данная процедура переводит цепную дробь в рациональную.

Алгоритм.

Умножаем последний элемент цепной дроби с предпоследним и прибавляем к полученному значению единицу, это будет значением числителя, значением знаменателя будет последний элемент цепной дроби, меняем их местами, теперь последним элементом цепной дроби будет полученный знаменатель; так делаем, пока не закончатся элементы цепной дроби.

Пример. Цепная дробь: [2,3,4,5]. Рациональная дробь: 157/68

Тесты.

1. Некорректные данные

2. Корректные данные

4. Заключение

Разработана программа CalcKurs, выполняющая следующие функции:

1. формирование заданного подмножества натурального ряда с помощью общего делителя;

2. факторизация числа с опциями;

3. нахождение НОД и НОК для заданной совокупности натурального ряда;

4. нахождение рациональных решений уравнения с целочисленными коэффициентами;

5. представление рациональной дроби в виде цепной;

6. представление цепной дроби в виде рациональной.

К минусам программы можно отнести невысокую размерность чисел, которые участвуют в вычислениях (-2147483648. .2147483647), некоторые алгоритмы можно сделать более оптимальными.

К плюсам можно отнести простоту в пользовании программой, её малую требовательность к ресурсам компьютера, программа исполняет основополагающие алгоритмы теории чисел. Она может помочь в изучении данного раздела математики.

Список использованных источников

1.http://ru. wikipedia.org/wiki/Теория_чисел

2.http://www.krugosvet.ru/enc/nauka_i_tehnika/matematika/CHISEL_TEORIYA.html

3.http://ru. wikipedia.org/wiki/Решето_Эратосфена

4.http://ru. wikipedia.org/wiki/Наибольший_общий_делитель

5.http://ru. wikipedia.org/wiki/Наименьшее_общее_кратное

6.http://ru. wikipedia.org/wiki/Метод_Горнера

7.http://dic. academic.ru/dic. nsf/es/39322/непрерывная

Приложение

Листинг программы

program kurs;

uses crt;

function pow (a,x: longint): longint;

var

t, i: longint;

begin

t: =a;

for i: =1 to x-1 do

t: =t*a;

pow: =t;

end; {pow}

{----------------------------------------}

procedure DelOstatok;

var

dd: array [1.200] of integer;

R: integer; {размерность чисел}

i: longint; {делитель}

k: longint; {остаток}

D,a,b: longint; {элементы заданного множества}

SUM: longint; {кол-во эл-ов, удовл условию}

S,T: byte;

q: char;

e,j,l,n: integer;

maxa,minj,maxj: longint;

begin

repeat

begin

writeln ('введите ко-во чисел для нахождения НОК делителей');

readln (n);

writeln ('введите ',n,' чисел: ');

readln (dd [1]);

maxa: =dd [1] ;

for i: =2 to n do

begin

readln (dd [i]);

if dd [i] >maxa then maxa: =dd [i] ;

end;

i: =1; while (dd [i] <>0) and (i<=n) do inc (i);

if i<>n+1 then writeln ('НОК не сущ-ет')

else begin

e: =1;

for i: =2 to maxa do

begin

maxj: =0;

for l: =1 to n do

begin

j: =0;

while (dd [l] mod i=0) do

begin

dd [l]: =dd [l] div i;

inc (j);

end;

if (j>maxj) then maxj: =j;

end;

if (maxj<>0) then for l: =1 to maxj do e: =e*i;

end;

writeln ('НОК делителей=',e);

end;

end;

i: =e;

write ('введите остаток=');

readln (k);

if ( (i<=0) or (k<0)) then {проверка

{вывод эл-ов на экран}

end; writeln;

end;

writeln ('Повторить? (Y/N) ');

q: =ReadKey;

until q in ['N','n'] ;

clrscr;

end; {DelOstatok}

{----------------------------------------}

procedure Factor;

var

numb, powers: array [1. .100] of longint;

c: longint;

n: longint;

n1,H: longint;

i: longint;

k,t: longint;

q: char;

begin

repeat

write ('Введите число=');

readln (c);

if c<=0 then {проверка на корр числа}

begin

writeln ('число должно быть>0');

readln;

exit;

end

else

{вывод мн-ва делителей}

begin

write ('мн-во делителей: D (num) =');

for H: = 1 to c do

if c mod H=0 then

write (H,' ');

end;

{конец вывода делителей}

n: = 1;

n1: = 0;

while c <> 1 do

begin

i: = 2;

while c mod i <> 0 do {проверка на делимостьс/без остатка}

Inc (i);

Inc (n1);

if n1 = 1 then

begin

numb [n]: = i;

powers [n]: = 1;

end

else

if numb [n] = i then Inc (powers [n])

else

begin

Inc (n); {увеличение кол-ва простых множителей}

numb [n]: = i;

powers [n]: = 1;

end; {while}

c: = c div i; {деление числа на простой множитель}

end; {while}

{\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\}

writeln;

writeln ('кол-во простых множителей: ',n);

write ('num = ');

k: =1;

t: =1;

writeln ('НОД=',k);

if k=1 then writeln ('числа взаимно простые');

end;

begin

i: =1; while (b [i] <>0) and (i<=n) do inc (i);

if i<>n+1 then writeln ('НОК не сущ-ет')

else begin

d: =1;

for i: =2 to maxa do

begin

maxj: =0;

for l: =1 to n do

begin

j: =0;

while (b [l] mod i=0) do

begin

b [l]: =b [l] div i;

inc (j);

end;

if (j>maxj) then maxj: =j;

end;

if (maxj<>0) then for l: =1 to maxj do d: =d*i;

end;

writeln ('НОК=',d);

end;

end;

end;

writeln ('Повторить? (Y/N) ');

q: =ReadKey;

until q in ['N','n'] ;

clrscr;

end; {NodNok}

{----------------------------------------}

procedure SuperGorner;

type

vector= array [1. .11] of integer;

rvector=array [1. .100] of real;

var

sum,suma: real;

i,k,j,b,c,a,n: integer;

vec: vector;

vecb: rvector;

veca: rvector;

q: char;

BEGIN

Writeln ('Введите степень уравнения (max = 10) ');

Readln (n);

if n<=0 then writeln (‘степень не может быть<=0’)

else begin

Inc (n);

writeln ('введите его коэффициенты: ');

for i: = 1 to n do

read (vec [i]);

while vec [i] =0 do

Begin

i: =i-1;

writeln ('ответ: 0');

End;

k: =1;

b: =vec [i] ;

for j: =1 to abs (b) do

begin

if (b mod j) =0 then

begin

vecb [k]: =j;

k: =k+1;

procedure AntiExp;

var s: array [1. .100] of integer;

a,b, i,n,t: integer;

q: char;

begin

repeat

writeln ('введите кол-во эл-ов цепной дроби=');

read (n);

if n<=0 then writeln (‘кол-во эл-ов не может быть<=0’)

else begin

writeln ('введите значения этих эл-ов=');

for i: =1 to n do

read (s [i]);

a: =1; b: =s [n] ;

for i: = n downto 2 do

begin

t: =s [i-1] *b+a;

a: =b;

b: =t;

end;

writeln;

writeln (b,'/',a);

end;

writeln ('Повторить? (Y/N) ');

q: =ReadKey;

until q in ['N','n'] ;

clrscr;

end; {AntiExp}

{----------------------------------------}

var

k: integer;

q: char;

begin

writeln ('Дискретная математика');

writeln ('Курсовая работа, группа 03-119, каф308');

writeln ('выполнил: Тузов И.И. ');

writeln ('руководитель: Гридин А.Н. ');

writeln;

writeln ('Калькулятор с функциями, описанными ниже');

writeln;

Writeln ('Нажмите Enter');

readln;

clrscr;

repeat

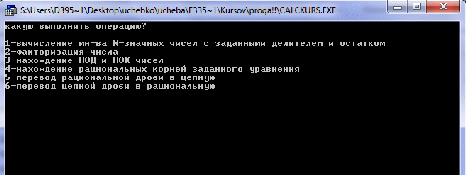
writeln ('Какую выполнить операцию? ');

writeln;

writeln ('1-вычисление мн-ва N-значных чисел с заданным делителем и остатком ');

writeln ('2-факторизация числа');

writeln ('3-нахождение НОД и НОК чисел');

writeln ('4-нахождение рационльных корней уравнения с целочисл коэфф');

writeln ('5-перевод рациональной дроби в цепную');

writeln ('6-перевод цепной дроби в рациональную');

read (k);

делителя и остатка на отриц-сть}

begin

write ('делитель или остаток не могут быть<0 ');

end

else

begin

if i>k then {проверка на делитель>остатка}

begin

write ('введите размерность=');

readln (R);

if R<=0 then

begin

writeln ('некорректная размерность ');

readln;

end

else begin

if R=1 then

begin a: =1; b: =9; end

else begin

a: =pow (10, (R-1)); {инициализация верх и нижн границ}

b: =pow (10,R);

b: =b-1;

end;

end;

if b<i then {проверка на делимое>делителя}

writeln ('делиоме не может быть < делителя ')

else

begin

SUM: =0; {обнуление сумы кол-ва эл-ов}

for D: = a to b do

begin

if (D mod i) =k then {проверка эл-ов на условие}

begin

SUM: =SUM+1;

end;

end;

writeln;

writeln ('кол-во эл-ов с делителем=', i: 3, ' и остатком=', k: 3, ' равно', SUM: 6);

end; {b

end {if i>k}

else

write ('остаток не может быть > делителя ');

end; {if otriz}

{\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\}

write ('вывести значения на экран? (1-да\0-нет) ');

readln (S);

if S=1 then

if SUM=0 then

writeln ('нет эл-ов, удовл. условию')

else

begin

for D: = a to b do

if (D mod i) =k then

begin

write (' ',D: 4);

{вычисление кол-ва делителей и их мн-ва}

for i: = 1 to n do

begin

write (numb [i], ' ^ ', powers [i]);

k: =k* ( (pow (numb [i],powers [i] +1) - 1) div (numb [i] - 1));

t: =t* (powers [i] +1); {кол-во делителей}

if i <> n then write (' * ');

end;

writeln;

writeln ('кол-во множителей: tau (num) =',t);

writeln ('сумма множителей: sigma (num) =',k);

writeln ('Повторить? (Y/N) ');

q: =ReadKey;

until q in ['N','n'] ;

clrscr;

end; {Factor}

{----------------------------------------}

procedure NodNok;

type TArray=array [1.200] of integer;

var a,b: TArray;

i,l,j,maxa,minj,maxj: longint;

k,d: longint;

n: integer;

q: char;

begin

repeat

clrscr;

writeln ('введите ко-во чисел для нахождения НОД и НОК');

readln (n);

writeln ('введите ',n,' чисел: ');

if n<=0 then writeln (‘кол-во чисел не может быть<=0’)

else begin

readln (a [1]);

b [1]: =a [1] ;

maxa: =a [1] ;

for i: =2 to n do

begin

readln (a [i]);

b [i]: =a [i] ;

if a [i] >maxa then maxa: =a [i] ;

end;

i: =1;

while (a [i] =0) and (i<=n) do inc (i);

if i=n+1 then writeln ('НОД - любое число')

else begin

for j: =1 to n do if a [j] =0 then a [j]: =a [i] ;

k: =1;

for i: =2 to maxa do

begin

minj: =1000;

for l: =1 to n do

begin

j: =0;

while (a [l] mod i=0) do

begin

a [l]: =a [l] div i;

inc (j);

end;

if (j

end;

if (minj<>0) then for l: =1 to minj do k: =k*i;

end;

vecb [k]: =-j;

k: =k+1;

end;

end;

a: =1;

for j: =1 to abs (vec [1]) do

begin

if (vec [1] mod j) =0 then

begin

veca [a]: =j;

a: =a+1;

{ veca [a]: =-j;

a: =a+1; }

End;

end;

b: =a;

for j: =1 to k-1 do

Begin

for a: =1 to b-1 do

Begin

Begin

c: =i;

sum: =0;

for i: =1 to c do

Begin

sum: =sum+vec [i] *pow1 (vecb [j] /veca [a],c-i);

if (sum<0.00001) and (sum>-0.00001) then

if vec [a] =1 then writeln ('ответ: ',round (vecb [j]))

else writeln ('ответ: ',round (vecb [j]), '/',round (veca [a]));

end;

End;

End;

End; end;

readln;

end; {SuperGorner}

{----------------------------------------}

procedure Express;

var

a,b,t: integer;

q: char;

begin

repeat

writeln ('введите числитель=');

readln (a);

writeln ('введите знаменатель=');

readln (b);

if b=0 then writeln (‘знаменатель не может быть=0’)

else begin

write (' [');

while (a mod b>0) do

begin

write (a div b,',');

a: =a mod b;

t: =b;

b: =a;

a: =t;

end;

write (a div b, '] ');

end;

writeln (‘Повторить? (Y/N) ');

q: =ReadKey;

until q in ['N','n'] ;

clrscr;

end; {Express}

{----------------------------------------}

case k of

1: DelOstatok;

2: Factor;

3: NodNok;

4: SuperGorner;

5: Express;

6: AntiExp;

else

writeln ('нет операции');

end; {case}

writeln ('Повторить выполнение калькулятора? (Y/N) ');

q: =ReadKey;

until q in ['N','n'] ;

clrscr;

readln;

end. {prog}