Інженерні розрахунки в MathCad

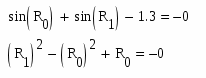
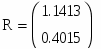
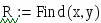
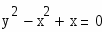
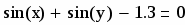
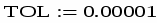
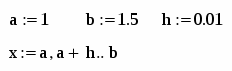
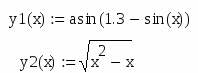
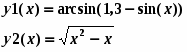
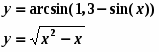
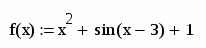
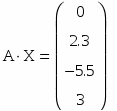
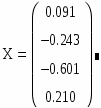
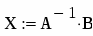
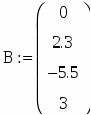
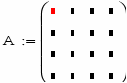
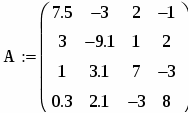
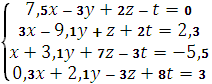Вступ

Тема контрольної роботи "Інженерні розрахунки в MathCad" з дисципліни "Інформатика".

Мета роботи - придбання навичок роботи з системою MathCad.

Завданні 1 передбачає розв’язання системи лінійних рівнянь у програмі MathCAD.

Завданні 2 передбачає розв’язання нелінійного рівняння за допомогою програми MathCAD.

Завданні 3 потребує знайти дійсні розв’язки системи нелінійних рівнянь із заданим ступенем точності в середовищі MathCAD.

Завдання

Завдання 1.

Задана система трьох лінійних рівнянь.

Знайти розв’язок системи матричним методом в середовищі MathCAD.

Розв’язання:

Розв’язання системи рівнянь у матричному виді проводиться за формулою

X=A^-1B,

деA - матриця, що складається з коефіцієнтів при невідомих,

А^-1 - обернена матриця до матриці А,

B - вектор вільних членів,

X - вектор розв'язків системи.

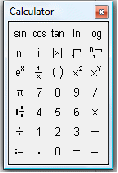
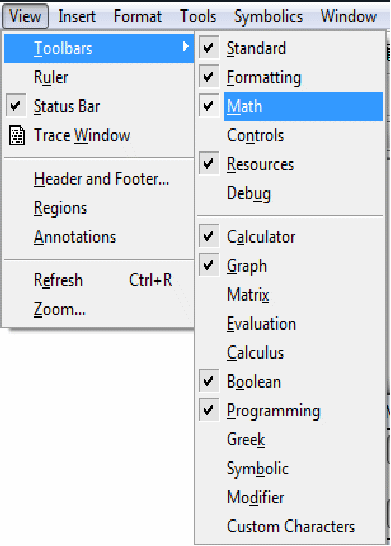
Для реалізації розрахунків в системі MathCAD необхідно скористатися панеллю інструментів Математика (Math):

яка визивається командою ViewToolbarsMath:

mathcad інженерний розрахунок рівняння

Кнопками панелі Математика необхідно визвати панелі:

Калькулятор (кнопкою ):

Матриця (кнопкою ):

А потім виконати наступні дії:

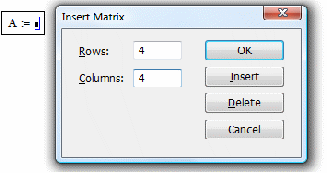
1. Створимо матрицю А:

Пояснення до виконуваних дій:

Використавши кнопку панелі Matrix:

Задаємо 4 рядки і 4 стовпці. А потім заповнюємо шаблон матриці коефіцієнтами системи:

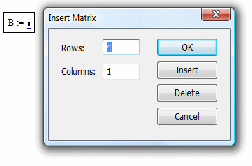
2. Створюємо вектор В:

Задаємо 4 рядки 1 стовпець:

Після чого заповнюємо маркери шаблону значеннями вільних членів системи:

3. Обраховуємо вектор Х:

Знак присвоєння: = вибираємо на панелі Calculator, обернену матрицю до матриці А створюємо за допомогою кнопки на панелі Matrix.

4. Виводимо результат розрахунків:

Результати рішення системи:

x = 0.091

y = - 0.243

z = - 0,601

t = 0.210

5. Робимо перевірку:

Розв’язок вірний, оскільки результат перемноження матриці А на вектор Х дорівнює вектору В.

Завдання 2

Знайти корінь нелінійного рівняння x³ + sin (x - 3) +1 = 0 з точністю  =0.0001

Розв’язання:

Всяке рівняння з одним невідомим може бути записане у вигляді f (x) = 0.

Знаходження наближеного значення дійсних коренів рівняння складається з двох етапів:

1 етап - відділення коренів - виділення відрізка, що належить області існування функції f (x), на якому розташований один і тільки один корінь. Для відділення коріння будують графік функції f (x). Абсциси точок перетину графіка функції y = f (x) з віссю ОХ і будуть наближеними значеннями коренів. По графіку легко вказати відрізки, на яких знаходиться один і тільки один корінь.

2 етап - уточнення наближених корінь, тобто обчислення їх із заданою точністю .

1 етап. Графічне відділення коренів рівняння.

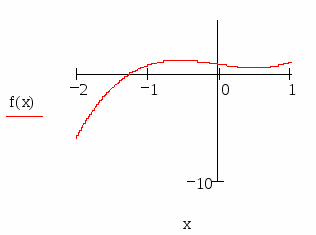
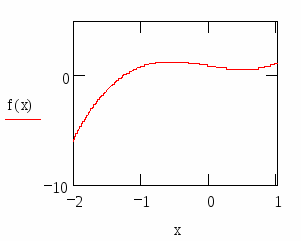
Побудуємо графік функції f (x) = x³ + sin (x - 3) +1.

Опишемо функцію в виді функції користувача:

Вставимо в документ графічну область командою InsertGraphXY-Plot:

Маркери () отриманого шаблону заповнимо відповідно іменем аргументу х і іменем функції f (x):

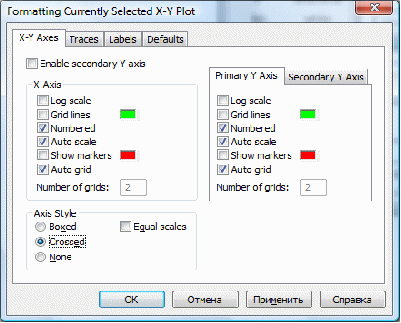
Відформатуємо графік командою FormatGraphXY-Plot:

Виберемо опцію Grossed (показувати осі координат):

Як видно із графіка функція f (x) перетинає вісь абсцис на інтервалі [-2; - 1]. Для подальших розрахунків приймемо наближене значення кореня x = - 1

2 етап - уточнення кореня до точністі  =0.0001.

Уточнення кореня, тобто доведення його до заданого ступеню точності проведемо за допомогою функції root (f (x), x).

Функція реалізує обчислення ітераційним методом, причому спочатку необхідно задати:

точність обчислень за допомогою системної змінної TOL;

початкове значення змінної х (будь-яке значення з відрізку визначеного на графіку).

Порядок дій:

TOL: =0.0001

Пояснення:

TOL - системна змінна, за допомогою якої задається точність обчислень в системі MathCAD.

x: = - 1

Початкова умова, знайдена із графіка.

x: = root (f (x), x)

x= - 1.2361

Застосування функції root для уточнення кореня.

Вивід значенння уточненого кореня х.

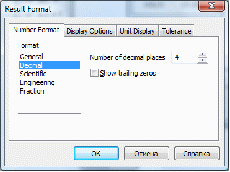
В установленому режимі MathCAD як правило виводить 3 десяткові знаки після коми. Оскільки задана точність  потребує 4 знаки, необхідно командою FormatResult… в вікні Result Format задати необхідне число знаків:

Отже корінь рівняння х= - 1,2361.

Завдання 3

Розв’язати систему нелінійних рівнянь:

sin (x) + sin (y) - 1.3 = 0

y² - x² +x = 0

с точністю =0.00001.

Розв’язання:

Відомо, що розв’язком системи є такі значення х і у, які перетворюють одночасно обидва рівняння в тотожності.

Для знаходження розв’язку системи необхідно спочатку графічно знайти грубе наближення цих значень для х і у.

Очевидно, що потрібно побудувати криві, які описуються рівняннями системи. Координати точки перетину цих кривих (як спільна їх точка) і являтимуть розв’язком системи.

Щоб побудувати ці криві необхідно рівняння системи привести до виду:

y = f1 (x)

y = f2 (x),

тобто в нашому випадку:

Після цього побудувати графіки функцій:

Порядок дій:

Пояснення:

Описуємо дві функції користувача

Функції asin, sin і  вибрати з панелі Calculator.

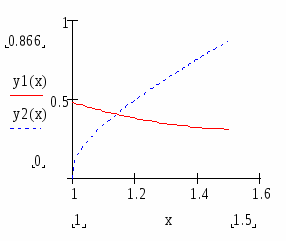
Будуємо графіки функцій: y1 (x) і y2 (x)

Довільно вибираємо відрізок [a,b], на якому будуємо графік функцій. Задаємо розбиття відрізку точками, описавши х як ранжовану змінну, яка змінюватиметься від а до b з кроком h.

Якщо на вибраному відрізку [a,b] криві не перетнуться змінюмо до тих пір а і b поки не віднайдемо точку перетину.

Із графіка приблизно знайти значення:

х=1,2 і у = 0,4

координати точки перетинання графіків

Задаємо початкові значення розвязку:

x: =1.2 y: = 0.4

Задаємо початкові значення для х і у.

Задаємо точність обчислень

Уточнюємо розвязок до задоного ступеня точності.

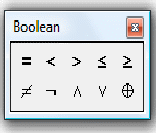
Для уточнення розв’язку використовуємо блок рішення, який відкривається директивою Given, а закривається функцією Find. В самому блоці записуються рівняння системи, в яких знак = вставляється з панелі

Вектору R присвоюється рішення системи.

Отже х = 1,1413 і у = 0,4015.

Проводимо перевірку розв’язку:

Перевірка розв’язку:

Замість х і у підставляємо в рівняння R₀ і R₁, які являються елементами вектора R (нумерація елементів починається з нуля).