Исследование методов оптимизации
 МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ
НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
«ХАРЬКОВСКИЙ ПОЛИТЕХНИЧЕСКИЙ ИНСТИТУТ»
Факультет информатики и управления
Кафедра экономической кибернетики и маркетингового менеджмента
КУРСОВАЯ РАБОТА
По математическому программированию
Исследование методов оптимизации
Харьков 2009
РЕФЕРАТ
Данная курсовая работа содержит : 41 страницу, 16 таблиц, 6 графиков.
В курсовой работе рассмотрены теоретические основы двух методов оптимизации математического программирования :
- метод Нелдера-Мида ;
- градиентный метод с дроблением шага.
Произведена минимизация исследуемой функции указанными методами. Выявлена зависимость числа итераций от заданной точности. Сопоставлена трудоемкость и эффективность оптимизации заданной функции различными методами (градиентным и методом Нелдера-Мида).
Ключевые термины:
Градиент – вектор первых частных производных функции.
Линии уровня – множества точек, в которых функция 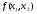 принимает постоянные значения, т.е.
принимает постоянные значения, т.е. 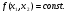
Методы нулевого порядка – методы, которые не предполагают вычисления производной для поиска оптимума.
Методы первого порядка – методы, в которых кроме вычисления функции в любой точке предлагается вычисление первых производных.
СОДЕРЖАНИЕ
1. Введение
2. Математическое описание методов оптимизации
2.1 Метод Нелдера-Мида
2.2 Градиентный метод с дроблением шага
3. Решение задачи минимизации для каждого из методов
3.1 Метод Нелдера-Мида
3.2 Градиентный метод с дроблением шага
4. Графическая интерпретация решения задачи
5. Аналитическое исследование методов
6. Заключение
7. Приложение
8. Список литературы
СПИСОК УСЛОВНЫХ ОБОЗНАЧЕНИЙ
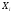 - точка
- точка
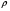 - длинна шага
- длинна шага
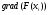 - вектор градиент
- вектор градиент
E - точность
N – количество итераций
Д – матрица координат симплекса
t – длинна ребра симплекса
1. ВВЕДЕНИЕ
Объектом исследования предмета математическое программирование являются задачи оптимизации.
Оптимизация подразумевает нахождение наилучшего варианта среди всех существующих. В любой практической оптимизационной задаче существует много совпадающих этапов. Наиболее важным этапом является моделирование рассматриваемой физической ситуации с целью получения математической функции, которую необходимо минимизировать, а также определения ограничений, если таковые существуют. Затем следует выбрать подходящую процедуру для осуществления минимизации. Эта процедура должна быть реализована на практике, что во многих реальных случаях вынуждает использовать ЭВМ для выполнения большого объема вычислений.
Универсальных методов, подходящих для поиска экстремума абсолютно любой функции не существует. Данная курсовая работа ставит себе целью исследовать метод оптимизации нулевого порядка – метод Нелдера-Мида, а также метод оптимизации первого порядка – градиентный метод с дроблением шага на примере конкретной функции. Таким образом, получив практические результаты, можно будет сравнить эффективность рассматриваемых методов, применяемых к исследуемой функции.
ПОСТАНОВКА ЗАДАЧИ ( Вариант задания 1)
Исследовать функцию типа :
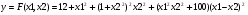
Используемые методы минимизации 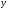 :
:
Метод: Нелдера-Мида.
Метод: Градиентный с дроблением шага.
Необходимо :
Решить задачу минимизации
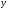 , начав итерации из выбранной начальной точки x0=(1;1) заданными по варианту методами, необходимая точность решения
, начав итерации из выбранной начальной точки x0=(1;1) заданными по варианту методами, необходимая точность решения 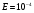 . Привести таблицу результатов расчета типа: Итерация:
. Привести таблицу результатов расчета типа: Итерация: 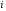 - точка:
- точка: 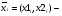 значение:
значение: 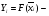 критерий:
критерий: 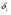 .
.Рассчитать 3 линии уровня функции и изобразить их на графике.
Отобразить на графиках линий уровня для каждого из заданных методов траекторию движения по итерациям (траекторию спуска).
Выявить зависимость числа итераций N от заданной точности E, значения точности:
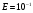 ,
, 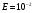 ,
, 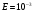 ,
, 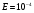 ,
, 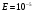 ,
, 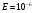 . Привести таблицу результатов как в п.1 для каждого значения E.
. Привести таблицу результатов как в п.1 для каждого значения E.
5. Сравнить эффективность рассмотренных в варианте методов по числу итераций N, построить графики N=F(E).
2. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ МЕТОДОВ ОПТИМИЗАЦИИ
2.1 Метод Нелдера-Мида
Вводится симплекс, координаты вершин которого заданы таблицей (одна из вершин в начале координат).
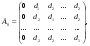
(n+1) точек
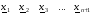

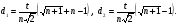
t – некоторое выбранное число.
Если n = 2, то при t = 1 имеем
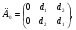
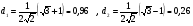
Расположение симплекса показано на рисунке 2.1
X1
X2
1
1
Рисунок 2.1- Начальное расположение симплекса
Легко убедиться в том, что если координаты вершин симплекса задать в соответствии с матрицей Д0 , то расстояние между двумя любыми вершинами симплекса всегда будет равно выбранной константе t независимо от размерности задачи n .
Действительно, расстояние между любой вершиной xj , j= 2,3,.., n+1, и вершиной x1 равно
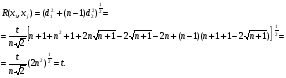
С другой стороны, расстояние между любой парой вершин 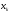 ,
, 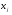 ,
, 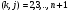 , равно
, равно 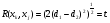 Зададим начальную точку процедуры поиска минимума вектором
Зададим начальную точку процедуры поиска минимума вектором 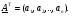 Перенесем исходный симплекс таким образом, чтобы вершина, находившаяся в начале координат, оказалась в точке
Перенесем исходный симплекс таким образом, чтобы вершина, находившаяся в начале координат, оказалась в точке 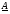 . Получим матрицу
. Получим матрицу
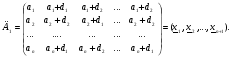
Вычислим значения оптимизируемой функции в точках 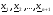 и переномеруем точки так, чтобы выполнялись неравенства :
и переномеруем точки так, чтобы выполнялись неравенства :
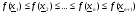 .
.
Найдем координаты центра тяжести фигуры , получающейся в результате удаления вершины 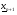 :
:
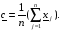
Осуществим отражение вершины 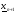 относительно центра тяжести. Получим точку
относительно центра тяжести. Получим точку
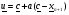 .
.
Если a=1 , то получим зеркальное отражение. В одномерном случае процедура отражения, обеспечивающая получение точки 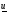 , симметричной точке
, симметричной точке 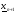 относительно
относительно 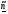 иллюстрируется рис. 2.2
иллюстрируется рис. 2.2
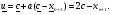
0
Xn+1
2c-xn+1
c
2c
Рисунок 2.2 - Построение точки 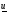
Сравним теперь между собой значения 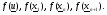
Возможны следующие варианты
а)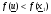 . В этом случае выполняется растяжение симплекса и отыскивается точка
. В этом случае выполняется растяжение симплекса и отыскивается точка 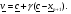
Параметр 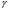 обычно принимается равным 1,5.
обычно принимается равным 1,5.
Полученная точка 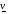 заменяет
заменяет 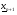 , если
, если 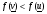 . В противном случае для замены
. В противном случае для замены 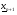 используется точка
используется точка 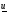 .
.
б) 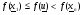 . При этом реализуется отражение. Точка
. При этом реализуется отражение. Точка 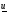 заменяет
заменяет 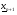 .
.
в) 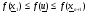 . В этом случае осуществляется сжатие и отыскивается точка
. В этом случае осуществляется сжатие и отыскивается точка 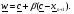
Параметр 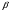 обычно принимается равным 0,5. Точка
обычно принимается равным 0,5. Точка 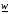 заменяет
заменяет 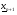 .
.
г) 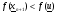 . При этом осуществляется редукция (уменьшение размера симплекса путем приближения всех его вершин к вершине
. При этом осуществляется редукция (уменьшение размера симплекса путем приближения всех его вершин к вершине 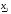 ). Координаты вершин нового симплекса рассчитываются по формулам
). Координаты вершин нового симплекса рассчитываются по формулам
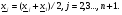
Критерий останова вычислительной процедуры имеет вид :
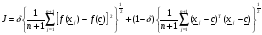
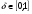
Критерий останова J является составным. При этом его компоненты имеют различный вес в зависимости от того, каков характер поведения оптимизируемой функции в окрестности экстремума. Если в районе экстремума оптимизируемая функция изменяется по типу «глубокая впадина», то больший вклад в численное значение критерия J вносит первое слагаемое, а второе при этом быстро уменьшается. Напротив, если оптимизируемая функция изменяется по типу «пологое плато», то первое слагаемое быстро становится малым и поэтому второе слагаемое вносит больший вклад в величину критерия J.
Модификация метода
Описанный «классический» вариант построения алгоритма метода Нелдера-Мида обладает конструктивным недостатком, который состоит в следующем. Предположим, что оптимизируемая функция, для простоты, двух переменных имеет вид глубокого оврага с очень пологим дном. Тогда может случиться так, что симплекс, который в рассматриваемом случае представляет собой треугольник, в какой-то момент двумя вершинами ляжет на дно оврага, а третья окажется на его склоне. При этом на очередном шаге произойдет переброс этой вершины на другой склон, а затем редукция или сжатие симплекса. Если склон оврага крутой, то эта процедура повторится много раз, в результате чего симплекс сожмется и может сработать критерий останова, хотя до точки минимума еще может быть очень далеко. Естественное усовершенствование алгоритма состоит в следующем. После срабатывания критерия останова целесообразно построить над центром тяжести сжавшегося симплекса новый, размеры которого соответствуют исходному симплексу. Пусть координаты центра тяжести сжавшегося симплекса образуют вектор
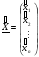 .
.
Найдем теперь координаты точки 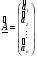 такой, что центр тяжести симплекса с длиной ребра, равной t , использующего вершину
такой, что центр тяжести симплекса с длиной ребра, равной t , использующего вершину 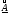 в качестве начальной, совпадал бы с
в качестве начальной, совпадал бы с 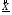 . Матрица координат указанного симплекса имеет вид
. Матрица координат указанного симплекса имеет вид
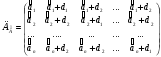 (2.1)
(2.1)
Координаты центра тяжести этого симплекса образуют вектор
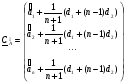
Теперь координаты точки 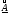 найдем из равенства
найдем из равенства 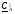 =
=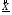 , откуда
, откуда
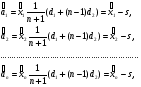
где 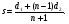
Подставляя вычисленные значения 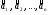 в выражение (2.1) , получим требуемый симплекс, используя который продолжим процедуру поиска минимума. С другой стороны, для продолжения процедуры в качестве начальной точки может быть использован центр тяжести «сжавшегося» симплекса. Возникающее при этом смещение нового симплекса относительно сжавшегося (точки предполагаемого останова) во многих случаях может даже оказаться полезным. Эту процедуру считаем законченной, если после очередного сжатия алгоритм приведет в точку, расстояние от которой до точки предыдущего сжатия
в выражение (2.1) , получим требуемый симплекс, используя который продолжим процедуру поиска минимума. С другой стороны, для продолжения процедуры в качестве начальной точки может быть использован центр тяжести «сжавшегося» симплекса. Возникающее при этом смещение нового симплекса относительно сжавшегося (точки предполагаемого останова) во многих случаях может даже оказаться полезным. Эту процедуру считаем законченной, если после очередного сжатия алгоритм приведет в точку, расстояние от которой до точки предыдущего сжатия 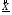 не превосходит некоторого достаточно малого
не превосходит некоторого достаточно малого 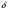 .
.
2.2 Градиентный метод с дроблением шага
Большей эффективностью обладают итерационные процедуры, в которых приближение к минимуму осуществляется сразу по всем переменным. При этом задача состоит в нахождении последовательности векторов 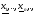 таких, что
таких, что
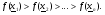 (2.2)
(2.2)
Методы построения таких последовательностей называют методами спуска. Пусть 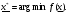 Поставим задачу отыскания последовательности
Поставим задачу отыскания последовательности 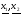 ., сходящейся к
., сходящейся к 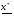 .
.
Выберем произвольным образом точку 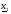 , направление
, направление 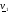 и сконструируем луч
и сконструируем луч
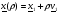 . (2.3)
. (2.3)
Рассмотрим вопрос о выборе направления 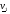 , обеспечивающего (2.2). Для этого изучим поведение
, обеспечивающего (2.2). Для этого изучим поведение 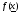 вдоль луча
вдоль луча 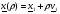 . Имеем
. Имеем 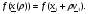
Введем
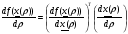 (2.4)
(2.4)
Здесь 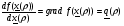
В соответствии с (2.3)
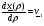
Тогда 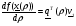
Вычислим 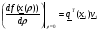 (2.5)
(2.5)
Теперь, чтобы для любого 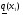 обеспечить отрицательность (2.5), достаточно положить
обеспечить отрицательность (2.5), достаточно положить 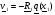 , где
, где 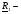 произвольная положительно определенная
произвольная положительно определенная 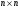 матрица. Тогда
матрица. Тогда
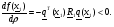
При этом 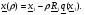 (2.6)
(2.6)
Выбрав каким-либо образом 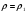 , получим
, получим 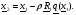 Затем аналогично рассчитаем
Затем аналогично рассчитаем 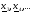
Общее рекуррентное соотношение имеет вид :
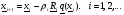 (2.7)
(2.7)
Различные варианты градиентных процедур отличаются друг от друга способом выбора 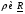 .
.
Полученное соотношение (2.7) обеспечивает построение последовательности точек 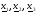 , сходящейся к точке
, сходящейся к точке 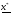 , минимизирующей
, минимизирующей 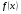 . Понятно, что каждая из точек этой последовательности может рассматриваться как некоторое приближение к точке минимума
. Понятно, что каждая из точек этой последовательности может рассматриваться как некоторое приближение к точке минимума 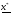 , положение которого, вообще говоря, остается неизвестным в ходе всей процедуры спуска. Поэтому для всех таких процедур принципиальной остается проблема останова. В вычислительной практике часто используются следующие критерии останова:
, положение которого, вообще говоря, остается неизвестным в ходе всей процедуры спуска. Поэтому для всех таких процедур принципиальной остается проблема останова. В вычислительной практике часто используются следующие критерии останова:
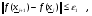 (2.8)
(2.8)
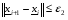 (2.9)
(2.9)
где 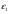 и
и 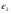 -некоторые достаточно малые числа .
-некоторые достаточно малые числа .
Понятно, что критерий (2.8) хорош в тех случаях, когда функция 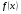 в окрестности минимума, используя ранее введенную классификацию, имеет характер «глубокой» впадины. С другой стороны, если функция
в окрестности минимума, используя ранее введенную классификацию, имеет характер «глубокой» впадины. С другой стороны, если функция 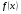 ведет себя как «пологое плато», то более предпочтительным является критерий (2.9). Аналогом критерия (2.8) является другое часто применяемое правило останова :
ведет себя как «пологое плато», то более предпочтительным является критерий (2.9). Аналогом критерия (2.8) является другое часто применяемое правило останова :
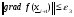 , (2.10)
, (2.10)
использующее необходимое условие экстремума функции. Очевидным недостатком критериев (2.8)-(2.10) является то, что их качество существенно зависит от абсолютных значений величины 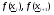 и компонентов векторов
и компонентов векторов 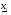 ,
,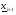 . Более универсальными являются относительные критерии :
. Более универсальными являются относительные критерии :
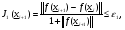 (2.11)
(2.11)
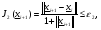 (2.12)
(2.12)
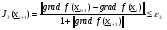 (2.13)
(2.13)
Заметим, что очень часто на практике используются составные критерии, представляющие собой линейную комбинацию критериев (2.11)-(2.13), например,
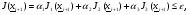
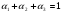
Иногда применяют другой вариант построения составного критерия :
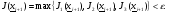
При реализации градиентного метода с дроблением шага в качестве 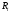 выбирают единичную матрицу, то есть
выбирают единичную матрицу, то есть
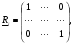
а длину шага определяют путем проверки некоторого неравенства. При этом основное рекуррентное соотношение (2.7) приобретает вид :
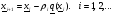
Ясно, то если 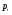 , выбирать достаточно малым, то это обеспечит убывание
, выбирать достаточно малым, то это обеспечит убывание 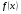 , но потребуется весьма большое число шагов. Если же неосторожно выбрать
, но потребуется весьма большое число шагов. Если же неосторожно выбрать 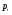 большим , то можно проскочить минимум, а это опасно в связи с возможным осциллированием. Для выбора шага используется правило Голдстейна-Армийо :
большим , то можно проскочить минимум, а это опасно в связи с возможным осциллированием. Для выбора шага используется правило Голдстейна-Армийо :
а) 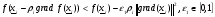 (2.14)
(2.14)
б) 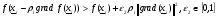 (2.15)
(2.15)
Выполнение условия а) обеспечивает выбор 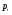 не слишком большим. Выполнение условия б) не дает возможность выбрать
не слишком большим. Выполнение условия б) не дает возможность выбрать 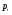 слишком малым.
слишком малым.
Практическая процедура строится следующим образом. Выбирается начальная точка 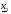 и некоторое начальное значение
и некоторое начальное значение 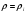 , проверяется (2.14) и, если оно выполняется, то делается шаг в направлении
, проверяется (2.14) и, если оно выполняется, то делается шаг в направлении 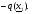 В новой точке
В новой точке 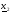 вычисляется градиент
вычисляется градиент 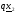 и вновь проверяется условие (2.14). В случае его удовлетворения продвижение к минимуму продолжается с тем же шагом. Если же оно не удовлетворяется, то параметр
и вновь проверяется условие (2.14). В случае его удовлетворения продвижение к минимуму продолжается с тем же шагом. Если же оно не удовлетворяется, то параметр 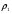 , определяющий длину шага, делят пополам до тех пор, пока это неравенство не будет выполнено. Затем выполняется очередной шаг. Процедура продолжается до выполнения критерия останова.
, определяющий длину шага, делят пополам до тех пор, пока это неравенство не будет выполнено. Затем выполняется очередной шаг. Процедура продолжается до выполнения критерия останова.
РЕШЕНИЕ ЗАДАЧИ МИНИМИЗАЦИИ ДЛЯ КАЖДОГО ИЗ МЕТОДОВ
Метод Нелдера-Мида
Построим симплекс состоящий из 3-х вершин. Длину ребра t возьмем равной 1 .
Начальные координаты симплекса :
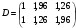
Проводим сортировку по значениям функции для поиска точки с наименьшей функцией. Далее записываем симплекс таким образом, чтобы первая точка была лучшей, а каждая последующая – хуже.
Для осуществления оптимизации вычислим новую точку как отражение самой «плохой» вершины относительно центра тяжести симплекса. Формула для вычисления новой точки:
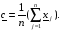
Затем, после сравнения значения функции в новой точке со значениями функции в остальных трех, а также после осуществления одного из четырех действий (замены, сжатия, растяжения и редукции), строится новый симплекс.
Одно из четырех действий, указанных выше, выполняется в соответствии с значением функции в новой точке, по отношению к значению функции в старых точках.
Замена происходит в случае, если новая точка лучше чем лучшая.
Если выполняется условие 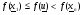 , то при этом реализуется отражение. Точка
, то при этом реализуется отражение. Точка 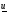 заменяет
заменяет 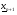 .
.
При выполнении условия 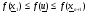 осуществляется сжатие и отыскивается точка
осуществляется сжатие и отыскивается точка 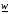 :
:
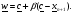
Параметр 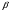 принимается равным 0,5. Точка
принимается равным 0,5. Точка 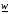 заменяет
заменяет 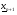 . Таким образом полученная точка заменяет самую «плохую»
. Таким образом полученная точка заменяет самую «плохую»
Если новая точка окажется самой «плохой», необходимо осуществить редукцию (уменьшение размера симплекса путем приближения всех его вершин к лучшей вершине)
После выполнения указанных действий проверяется параметр останова. В случае, если он признан большим, чем выбранное значение точности, действия повторяются снова. Параметр останова рассчитывается по формуле :
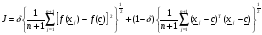
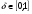
Результат работы метода представлен в таблице 3.1
Таблица 3.1 – Решение задачи минимизации при помощи метода Нелдера-Мида
Номер итерации
Х1
Х2
Функция
Параметр останова
1
0,4066667
0,4066667
45,631123492267
14,5885289
2
0,4433333
0,2683333
29,870063661634
2,8471538
3
0,3141667
0,2704167
16,456883364840
0,8308005
4
0,2495833
0,2714583
13,667862520021
0,3301516
5
0,2194792
0,2030729
12,662220410942
0,1540974
6
0,1796615
0,1864974
12,281326901893
0,0870517
7
0,1546549
0,1481608
12,136891733007
0,0558708
8
0,1284945
0,1302889
12,072845463097
0,0394655
9
0,1094511
0,1066526
12,044325208099
0,0355389
10
0,0380868
0,0472725
12,032057545239
0,0204381
11
0,0107240
0,0206094
12,021017539213
0,0124410
12
0,0217244
0,0287886
12,011093940034
0,0130068
13
-0,0220008
-0,0163585
12,008732867306
0,0089109
14
-0,0274319
-0,0235556
12,005248404276
0,0053110
15
-0,0178584
-0,0140681
12,003293104515
0,0042019
16
-0,0191470
-0,0189750
12,002069416305
0,0030794
17
-0,0146824
-0,0154579
12,001121615618
0,0025320
18
-0,0132441
-0,0133520
12,000655246493
0,0026725
19
-0,0028766
-0,0042119
12,000504634754
0,0015212
20
0,0004344
-0,0008739
12,000339347268
0,0009248
21
-0,0013297
-0,0023245
12,000183034613
0,0009948
22
0,0035282
0,0029010
12,000137117579
0,0007582
23
0,0038607
0,0034821
12,000078476732
0,0004900
24
0,0027293
0,0023210
12,000050320679
0,0004156
25
0,0022628
0,0023222
12,000031684386
0,0002830
26
0,0015804
0,0017419
12,000017894979
0,0002411
27
0,0015265
0,0015966
12,000009969113
0,0002705
28
0,0001079
0,0002907
12,000008036464
0,0001594
29
-0,0002737
-0,0001084
12,000005403290
0,0000921
В результате решения задачи минимизации с помощью метода Нелдера-Мида получено следующее значение функции : 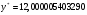 . Данный оптимум достигается в точке
. Данный оптимум достигается в точке 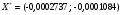 . Этот метод позволяет найти минимум (при начальной точке Х (1 ; 1)) за 29 итераций при точности решения
. Этот метод позволяет найти минимум (при начальной точке Х (1 ; 1)) за 29 итераций при точности решения 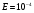 . При этом параметр останова равен 0,0000921.
. При этом параметр останова равен 0,0000921.
Градиентный метод с дроблением шага
Для реализации процедуры необходимо вычислить градиент:
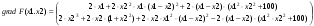
В процедуре используется критерий останова, который вычисляется по формуле:
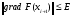 ,
,
где E – заданная точность решения (в данной задаче E=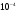 ).
).
Результат работы метода представлен в таблице 3.2
Вследствие того, что таблица содержит 1263 итерации, целесообразно предоставить первые и последние 25 итераций.
Таблица 3.2 – Решение задачи минимизации при помощи градиентного метода
Номер итерации
Х1
Х2
Функция
Параметр останова
1
0,992187500
0,976562500
14,872248322711100
5,725771436
2
0,972112596
0,966700991
14,755778561425900
5,391343315
3
0,960252606
0,949298075
14,647453457158200
5,170831157
4
0,944120479
0,937143394
14,545808827169400
4,999364954
5
0,931250704
0,922455245
14,450015755630300
4,851038521
6
0,917052669
0,909905567
14,359522419103900
4,715343849
7
0,904265341
0,896648294
14,273894939963900
4,588117156
8
0,891210499
0,884368998
14,192768112137200
4,467486611
9
0,878869537
0,872030350
14,115817843495700
4,352565782
10
0,866628626
0,860230552
14,042753034754000
4,242801681
11
0,854831609
0,848589700
13,973308662686200
4,137814211
12
0,843250897
0,837314037
13,907242987828300
4,037283606
13
0,832001542
0,826261206
13,844334505896600
3,940936337
14
0,820995553
0,815497743
13,784380045189000
3,848521743
15
0,810266979
0,804966957
13,727192808899800
3,759812059
16
0,799778396
0,794686358
13,672600853099300
3,674595835
17
0,789535800
0,784630345
13,620445636362400
3,592677880
18
0,779520366
0,774799711
13,570580790710000
3,513876598
19
0,769728817
0,765180416
13,522870992857600
3,438023378
20
0,760149472
0,755767918
13,477190974079800
3,364961115
21
0,750776352
0,746552749
13,433424623226000
3,294543452
22
0,741600798
0,737528983
13,391464187766000
3,226633778
23
0,732616368
0,728689198
13,351209552529500
3,161104506
24
0,723815911
0,720027406
13,312567592195300
3,097836320
25
0,715193248
0,711537292
13,275451586431100
3,036717546
1239
0,000042461
0,000042461
12,000000003605800
0,000120097
1240
0,000042129
0,000042129
12,000000003549700
0,000119159
1241
0,000041800
0,000041800
12,000000003494500
0,000118228
1242
0,000041473
0,000041473
12,000000003440100
0,000117304
1243
0,000041149
0,000041149
12,000000003386500
0,000116388
1244
0,000040828
0,000040828
12,000000003333800
0,000115479
1245
0,000040509
0,000040509
12,000000003281900
0,000114576
1246
0,000040192
0,000040192
12,000000003230900
0,000113681
1247
0,000039878
0,000039878
12,000000003180600
0,000112793
1248
0,000039567
0,000039567
12,000000003131100
0,000111912
1249
0,000039258
0,000039258
12,000000003082300
0,000111038
1250
0,000038951
0,000038951
12,000000003034400
0,000110170
1251
0,000038647
0,000038647
12,000000002987100
0,000109309
1252
0,000038345
0,000038345
12,000000002940600
0,000108455
1253
0,000038045
0,000038045
12,000000002894900
0,000107608
1254
0,000037748
0,000037748
12,000000002849800
0,000106767
1255
0,000037453
0,000037453
12,000000002805500
0,000105933
1256
0,000037161
0,000037161
12,000000002761800
0,000105106
1257
0,000036870
0,000036870
12,000000002718800
0,000104285
1258
0,000036582
0,000036582
12,000000002676500
0,000103470
1259
0,000036296
0,000036296
12,000000002634800
0,000102662
1260
0,000036013
0,000036013
12,000000002593800
0,000101860
1261
0,000035731
0,000035731
12,000000002553500
0,000101064
1262
0,000035452
0,000035452
12,000000002513700
0,000100274
1263
0,000035175
0,000035175
12,000000002474600
0,000099491
В результате реализации градиентного метода минимальное значение функции составляет 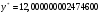 . Данный оптимум достигнут в точке
. Данный оптимум достигнут в точке 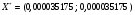 . Этот метод позволяет найти минимум (при начальной точке Х(1;1) за 1263 итерации при точности решения
. Этот метод позволяет найти минимум (при начальной точке Х(1;1) за 1263 итерации при точности решения 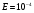 . При этом параметр останова равен 0,000099491.
. При этом параметр останова равен 0,000099491.
4. ГРАФИЧЕСКАЯ ИНТЕРПРИТАЦИЯ РЕШЕНИЯ ЗАДАЧИ
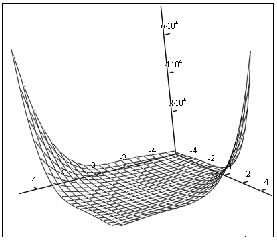
График исследуемой функции 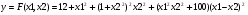 имеет вид :
имеет вид :
Рисунок 4.1 – График исследуемой функции
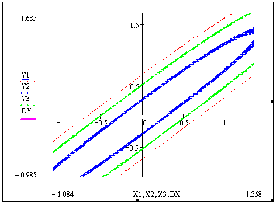
Изобразим на рисунке (4.2) линии уровня функции
Рисунок 4.2 – Линии уровня исследуемой функции
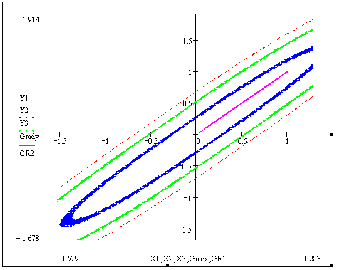
Отобразим на графиках линий уровня для каждого из заданных методов траекторию спуска
Рисунок 4.3 – траектория спуска (метод Нелдера-Мида)
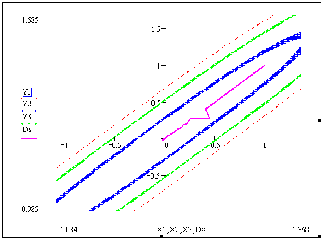
Рисунок 4.4 – траектория спуска (градиентный метод)
АНАЛИТИЧЕСКОЕ ИССЛЕДОВАНИЕ МЕТОДОВ
Для выявления зависимости числа итераций от заданной точности методы реализованы для каждого значения точности. Результаты представлены в таблицах (5.1-5.6, 5.8-5.13)
Реализация метода Нелдера-Мида :
Таблица 5.1 – Реализация метода Нелдера-Мида при 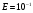
Номер итерации
Х1
Х2
Функция
Параметр останова
1
0,4066667
0,4066667
45,631123492267
14,5885289
2
0,4433333
0,2683333
29,870063661634
2,8471538
3
0,3141667
0,2704167
16,456883364840
0,8308005
4
0,2495833
0,2714583
13,667862520021
0,3301516
5
0,2194792
0,2030729
12,662220410942
0,1540974
6
0,1796615
0,1864974
12,281326901893
0,0870517
Таблица 5.2 – Реализация метода Нелдера-Мида при 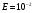
Номер итерации
Х1
Х2
Функция
Параметр останова
1
0,4066667
0,4066667
45,631123492267
14,5885289
2
0,4433333
0,2683333
29,870063661634
2,8471538
3
0,3141667
0,2704167
16,456883364840
0,8308005
4
0,2495833
0,2714583
13,667862520021
0,3301516
5
0,2194792
0,2030729
12,662220410942
0,1540974
6
0,1796615
0,1864974
12,281326901893
0,0870517
7
0,1546549
0,1481608
12,136891733007
0,0558708
8
0,1284945
0,1302889
12,072845463097
0,0394655
9
0,1094511
0,1066526
12,044325208099
0,0355389
10
0,0380868
0,0472725
12,032057545239
0,0204381
11
0,0107240
0,0206094
12,021017539213
0,0124410
12
0,0217244
0,0287886
12,011093940034
0,0130068
13
-0,0220008
-0,0163585
12,008732867306
0,0089109
Таблица 5.3 – Реализация метода Нелдера-Мида при 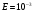
Номер итерации
Х1
Х2
Функция
Параметр останова
1
0,4066667
0,4066667
45,631123492267
14,5885289
2
0,4433333
0,2683333
29,870063661634
2,8471538
3
0,3141667
0,2704167
16,456883364840
0,8308005
4
0,2495833
0,2714583
13,667862520021
0,3301516
5
0,2194792
0,2030729
12,662220410942
0,1540974
6
0,1796615
0,1864974
12,281326901893
0,0870517
7
0,1546549
0,1481608
12,136891733007
0,0558708
8
0,1284945
0,1302889
12,072845463097
0,0394655
9
0,1094511
0,1066526
12,044325208099
0,0355389
10
0,0380868
0,0472725
12,032057545239
0,0204381
11
0,0107240
0,0206094
12,021017539213
0,0124410
12
0,0217244
0,0287886
12,011093940034
0,0130068
13
-0,0220008
-0,0163585
12,008732867306
0,0089109
14
-0,0274319
-0,0235556
12,005248404276
0,0053110
15
-0,0178584
-0,0140681
12,003293104515
0,0042019
16
-0,0191470
-0,0189750
12,002069416305
0,0030794
17
-0,0146824
-0,0154579
12,001121615618
0,0025320
18
-0,0132441
-0,0133520
12,000655246493
0,0026725
19
-0,0028766
-0,0042119
12,000504634754
0,0015212
20
0,0004344
-0,0008739
12,000339347268
0,0009248
Таблица 5.4 – Реализация метода Нелдера-Мида при 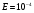
Номер итерации
Х1
Х2
Функция
Параметр останова
1
0,4066667
0,4066667
45,631123492267
14,5885289
2
0,4433333
0,2683333
29,870063661634
2,8471538
3
0,3141667
0,2704167
16,456883364840
0,8308005
4
0,2495833
0,2714583
13,667862520021
0,3301516
5
0,2194792
0,2030729
12,662220410942
0,1540974
6
0,1796615
0,1864974
12,281326901893
0,0870517
7
0,1546549
0,1481608
12,136891733007
0,0558708
8
0,1284945
0,1302889
12,072845463097
0,0394655
9
0,1094511
0,1066526
12,044325208099
0,0355389
10
0,0380868
0,0472725
12,032057545239
0,0204381
11
0,0107240
0,0206094
12,021017539213
0,0124410
12
0,0217244
0,0287886
12,011093940034
0,0130068
13
-0,0220008
-0,0163585
12,008732867306
0,0089109
14
-0,0274319
-0,0235556
12,005248404276
0,0053110
15
-0,0178584
-0,0140681
12,003293104515
0,0042019
16
-0,0191470
-0,0189750
12,002069416305
0,0030794
17
-0,0146824
-0,0154579
12,001121615618
0,0025320
18
-0,0132441
-0,0133520
12,000655246493
0,0026725
19
-0,0028766
-0,0042119
12,000504634754
0,0015212
20
0,0004344
-0,0008739
12,000339347268
0,0009248
21
-0,0013297
-0,0023245
12,000183034613
0,0009948
22
0,0035282
0,0029010
12,000137117579
0,0007582
23
0,0038607
0,0034821
12,000078476732
0,0004900
24
0,0027293
0,0023210
12,000050320679
0,0004156
25
0,0022628
0,0023222
12,000031684386
0,0002830
26
0,0015804
0,0017419
12,000017894979
0,0002411
27
0,0015265
0,0015966
12,000009969113
0,0002705
28
0,0001079
0,0002907
12,000008036464
0,0001594
29
-0,0002737
-0,0001084
12,000005403290
0,0000921
Таблица 5.5 – Реализация метода Нелдера-Мида при 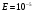
Номер итерации
Х1
Х2
Функция
Параметр останова
1
0,4066667
0,4066667
45,631123492267
14,5885289
2
0,4433333
0,2683333
29,870063661634
2,8471538
3
0,3141667
0,2704167
16,456883364840
0,8308005
4
0,2495833
0,2714583
13,667862520021
0,3301516
5
0,2194792
0,2030729
12,662220410942
0,1540974
6
0,1796615
0,1864974
12,281326901893
0,0870517
7
0,1546549
0,1481608
12,136891733007
0,0558708
8
0,1284945
0,1302889
12,072845463097
0,0394655
9
0,1094511
0,1066526
12,044325208099
0,0355389
10
0,0380868
0,0472725
12,032057545239
0,0204381
11
0,0107240
0,0206094
12,021017539213
0,0124410
12
0,0217244
0,0287886
12,011093940034
0,0130068
13
-0,0220008
-0,0163585
12,008732867306
0,0089109
14
-0,0274319
-0,0235556
12,005248404276
0,0053110
15
-0,0178584
-0,0140681
12,003293104515
0,0042019
16
-0,0191470
-0,0189750
12,002069416305
0,0030794
17
-0,0146824
-0,0154579
12,001121615618
0,0025320
18
-0,0132441
-0,0133520
12,000655246493
0,0026725
19
-0,0028766
-0,0042119
12,000504634754
0,0015212
20
0,0004344
-0,0008739
12,000339347268
0,0009248
21
-0,0013297
-0,0023245
12,000183034613
0,0009948
22
0,0035282
0,0029010
12,000137117579
0,0007582
23
0,0038607
0,0034821
12,000078476732
0,0004900
24
0,0027293
0,0023210
12,000050320679
0,0004156
25
0,0022628
0,0023222
12,000031684386
0,0002830
26
0,0015804
0,0017419
12,000017894979
0,0002411
27
0,0015265
0,0015966
12,000009969113
0,0002705
28
0,0001079
0,0002907
12,000008036464
0,0001594
29
-0,0002737
-0,0001084
12,000005403290
0,0000921
30
-0,0000145
0,0001182
12,000003012890
0,0000930
31
-0,0005185
-0,0004534
12,000002135678
0,0000765
32
-0,0005149
-0,0004829
12,000001171711
0,0000537
33
-0,0003880
-0,0003474
12,000000755753
0,0000486
34
-0,0002538
-0,0002710
12,000000487650
0,0000301
35
-0,0001568
-0,0001842
12,000000290103
0,0000249
36
-0,0001661
-0,0001816
12,000000155619
0,0000289
37
0,0000186
-0,0000052
12,000000128281
0,0000180
38
0,0000601
0,0000402
12,000000084592
0,0000102
39
0,0000243
0,0000074
12,000000049029
0,0000094
Таблица 5.6 – Реализация метода Нелдера-Мида при 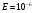
Номер итерации
Х1
Х2
Функция
Параметр останова
1
0,4066667
0,4066667
45,631123492267
14,5885289
2
0,4433333
0,2683333
29,870063661634
2,8471538
3
0,3141667
0,2704167
16,456883364840
0,8308005
4
0,2495833
0,2714583
13,667862520021
0,3301516
5
0,2194792
0,2030729
12,662220410942
0,1540974
6
0,1796615
0,1864974
12,281326901893
0,0870517
7
0,1546549
0,1481608
12,136891733007
0,0558708
8
0,1284945
0,1302889
12,072845463097
0,0394655
9
0,1094511
0,1066526
12,044325208099
0,0355389
10
0,0380868
0,0472725
12,032057545239
0,0204381
11
0,0107240
0,0206094
12,021017539213
0,0124410
12
0,0217244
0,0287886
12,011093940034
0,0130068
13
-0,0220008
-0,0163585
12,008732867306
0,0089109
14
-0,0274319
-0,0235556
12,005248404276
0,0053110
15
-0,0178584
-0,0140681
12,003293104515
0,0042019
16
-0,0191470
-0,0189750
12,002069416305
0,0030794
17
-0,0146824
-0,0154579
12,001121615618
0,0025320
18
-0,0132441
-0,0133520
12,000655246493
0,0026725
19
-0,0028766
-0,0042119
12,000504634754
0,0015212
20
0,0004344
-0,0008739
12,000339347268
0,0009248
21
-0,0013297
-0,0023245
12,000183034613
0,0009948
22
0,0035282
0,0029010
12,000137117579
0,0007582
23
0,0038607
0,0034821
12,000078476732
0,0004900
24
0,0027293
0,0023210
12,000050320679
0,0004156
25
0,0022628
0,0023222
12,000031684386
0,0002830
26
0,0015804
0,0017419
12,000017894979
0,0002411
27
0,0015265
0,0015966
12,000009969113
0,0002705
28
0,0001079
0,0002907
12,000008036464
0,0001594
29
-0,0002737
-0,0001084
12,000005403290
0,0000921
30
-0,0000145
0,0001182
12,000003012890
0,0000930
31
-0,0005185
-0,0004534
12,000002135678
0,0000765
32
-0,0005149
-0,0004829
12,000001171711
0,0000537
33
-0,0003880
-0,0003474
12,000000755753
0,0000486
34
-0,0002538
-0,0002710
12,000000487650
0,0000301
35
-0,0001568
-0,0001842
12,000000290103
0,0000249
36
-0,0001661
-0,0001816
12,000000155619
0,0000289
37
0,0000186
-0,0000052
12,000000128281
0,0000180
38
0,0000601
0,0000402
12,000000084592
0,0000102
39
0,0000243
0,0000074
12,000000049029
0,0000094
40
0,0000716
0,0000655
12,000000032997
0,0000081
41
0,0000655
0,0000636
12,000000017601
0,0000061
42
0,0000522
0,0000486
12,000000011215
0,0000059
43
0,0000267
0,0000299
12,000000007565
0,0000034
44
0,0000136
0,0000178
12,000000004741
0,0000026
45
0,0000167
0,0000194
12,000000002493
0,0000031
46
-0,0000062
-0,0000033
12,000000002045
0,0000021
47
-0,0000104
-0,0000081
12,000000001302
0,0000012
48
-0,0000057
-0,0000037
12,000000000784
0,0000010
49
-0,0000094
-0,0000089
12,000000000507
0,0000009
Данные по количеству итераций и заданным точностям для метода Нелдера-Мида сведены в таблицу 5.7
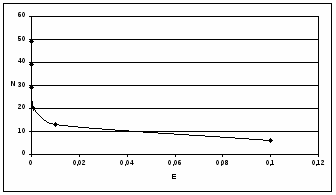
Таблица 5.7 - Зависимость числа итераций от точности
Точность
Количество итераций
0,1
6
0,01
13
0,001
20
0,0001
29
0,00001
39
0,000001
49
Рисунок 5.1 – Графическое представление зависимости количества итераций N от точности E для метода Нелдера-Мида.
Для градиентного метода, принимая во внимание большое количество итераций, целесообразно приводить для каждой реализации первые и последние 25 итераций.
Реализация градиентного метода:
Таблица 5.8 – Реализация градиентного метода при 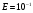
Номер итерации
Х1
Х2
Функция
Параметр останова
1
0,992187500
0,976562500
14,872248322711100
5,725771436
2
0,972112596
0,966700991
14,755778561425900
5,391343315
3
0,960252606
0,949298075
14,647453457158200
5,170831157
4
0,944120479
0,937143394
14,545808827169400
4,999364954
5
0,931250704
0,922455245
14,450015755630300
4,851038521
6
0,917052669
0,909905567
14,359522419103900
4,715343849
7
0,904265341
0,896648294
14,273894939963900
4,588117156
8
0,891210499
0,884368998
14,192768112137200
4,467486611
9
0,878869537
0,872030350
14,115817843495700
4,352565782
10
0,866628626
0,860230552
14,042753034754000
4,242801681
11
0,854831609
0,848589700
13,973308662686200
4,137814211
12
0,843250897
0,837314037
13,907242987828300
4,037283606
13
0,832001542
0,826261206
13,844334505896600
3,940936337
14
0,820995553
0,815497743
13,784380045189000
3,848521743
15
0,810266979
0,804966957
13,727192808899800
3,759812059
16
0,799778396
0,794686358
13,672600853099300
3,674595835
17
0,789535800
0,784630345
13,620445636362400
3,592677880
18
0,779520366
0,774799711
13,570580790710000
3,513876598
19
0,769728817
0,765180416
13,522870992857600
3,438023378
20
0,760149472
0,755767918
13,477190974079800
3,364961115
21
0,750776352
0,746552749
13,433424623226000
3,294543452
22
0,741600798
0,737528983
13,391464187766000
3,226633778
23
0,732616368
0,728689198
13,351209552529500
3,161104506
24
0,723815911
0,720027406
13,312567592195300
3,097836320
25
0,715193248
0,711537292
13,275451586431100
3,036717546
358
0,042588763
0,042587983
12,003630828695700
0,120676586
359
0,042255429
0,042254667
12,003574166022100
0,119728711
360
0,041924713
0,041923969
12,003518389968100
0,118788359
361
0,041596595
0,041595868
12,003463486588100
0,117855470
362
0,041271053
0,041270343
12,003409442157800
0,116929982
363
0,040948069
0,040947375
12,003356243171100
0,116011835
364
0,040627620
0,040626943
12,003303876336500
0,115100970
365
0,040309688
0,040309026
12,003252328573200
0,114197326
366
0,039994251
0,039993605
12,003201587008200
0,113300844
367
0,039681292
0,039680660
12,003151638972600
0,112411467
368
0,039370788
0,039370172
12,003102471998700
0,111529137
369
0,039062723
0,039062121
12,003054073816300
0,110653795
370
0,038757075
0,038756487
12,003006432349600
0,109785386
371
0,038453826
0,038453252
12,002959535714300
0,108923853
372
0,038152957
0,038152396
12,002913372214400
0,108069140
373
0,037854448
0,037853901
12,002867930339100
0,107221192
374
0,037558283
0,037557747
12,002823198760000
0,106379954
375
0,037264440
0,037263918
12,002779166327700
0,105545371
376
0,036972904
0,036972393
12,002735822069600
0,104717390
377
0,036683654
0,036683156
12,002693155186500
0,103895956
378
0,036396674
0,036396187
12,002651155050100
0,103081018
379
0,036111944
0,036111468
12,002609811200200
0,102272522
380
0,035829448
0,035828983
12,002569113341800
0,101470417
381
0,035549167
0,035548714
12,002529051343000
0,100674650
382
0,035271085
0,035270642
12,002489615231500
0,099885171
Таблица 5.9 – Реализация градиентного метода при 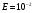
Номер итерации
Х1
Х2
Функция
Параметр останова
1
0,992187500
0,976562500
14,872248322711100
5,725771436
2
0,972112596
0,966700991
14,755778561425900
5,391343315
3
0,960252606
0,949298075
14,647453457158200
5,170831157
4
0,944120479
0,937143394
14,545808827169400
4,999364954
5
0,931250704
0,922455245
14,450015755630300
4,851038521
6
0,917052669
0,909905567
14,359522419103900
4,715343849
7
0,904265341
0,896648294
14,273894939963900
4,588117156
8
0,891210499
0,884368998
14,192768112137200
4,467486611
9
0,878869537
0,872030350
14,115817843495700
4,352565782
10
0,866628626
0,860230552
14,042753034754000
4,242801681
11
0,854831609
0,848589700
13,973308662686200
4,137814211
12
0,843250897
0,837314037
13,907242987828300
4,037283606
13
0,832001542
0,826261206
13,844334505896600
3,940936337
14
0,820995553
0,815497743
13,784380045189000
3,848521743
15
0,810266979
0,804966957
13,727192808899800
3,759812059
16
0,799778396
0,794686358
13,672600853099300
3,674595835
17
0,789535800
0,784630345
13,620445636362400
3,592677880
18
0,779520366
0,774799711
13,570580790710000
3,513876598
19
0,769728817
0,765180416
13,522870992857600
3,438023378
20
0,760149472
0,755767918
13,477190974079800
3,364961115
21
0,750776352
0,746552749
13,433424623226000
3,294543452
22
0,741600798
0,737528983
13,391464187766000
3,226633778
23
0,732616368
0,728689198
13,351209552529500
3,161104506
24
0,723815911
0,720027406
13,312567592195300
3,097836320
25
0,715193248
0,711537292
13,275451586431100
3,036717546
652
0,004240917
0,004240916
12,000035971071500
0,011995339
653
0,004207784
0,004207784
12,000035411204000
0,011901621
654
0,004174910
0,004174910
12,000034860050800
0,011808634
655
0,004142293
0,004142293
12,000034317476100
0,011716375
656
0,004109931
0,004109930
12,000033783346400
0,011624836
657
0,004077822
0,004077821
12,000033257530400
0,011534012
658
0,004045963
0,004045963
12,000032739898600
0,011443898
659
0,004014354
0,004014353
12,000032230323500
0,011354489
660
0,003982991
0,003982990
12,000031728679900
0,011265777
661
0,003951873
0,003951873
12,000031234844100
0,011177759
662
0,003920999
0,003920998
12,000030748694800
0,011090429
663
0,003890366
0,003890365
12,000030270112300
0,011003781
664
0,003859972
0,003859971
12,000029798978700
0,010917810
665
0,003829815
0,003829815
12,000029335178200
0,010832511
666
0,003799894
0,003799894
12,000028878596500
0,010747878
667
0,003770207
0,003770207
12,000028429121400
0,010663907
668
0,003740752
0,003740751
12,000027986642200
0,010580592
669
0,003711527
0,003711526
12,000027551050000
0,010497927
670
0,003682530
0,003682530
12,000027122237600
0,010415909
671
0,003653760
0,003653760
12,000026700099600
0,010334531
672
0,003625215
0,003625214
12,000026284531900
0,010253790
673
0,003596892
0,003596892
12,000025875432400
0,010173679
674
0,003568791
0,003568791
12,000025472700300
0,010094194
675
0,003540910
0,003540909
12,000025076236600
0,010015330
676
0,003513246
0,003513246
12,000024685943600
0,009937082
Таблица 5.10 – Реализация градиентного метода при 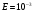
Номер итерации
Х1
Х2
Функция
Параметр останова
1
0,992187500
0,976562500
14,872248322711100
5,725771436
2
0,972112596
0,966700991
14,755778561425900
5,391343315
3
0,960252606
0,949298075
14,647453457158200
5,170831157
4
0,944120479
0,937143394
14,545808827169400
4,999364954
5
0,931250704
0,922455245
14,450015755630300
4,851038521
6
0,917052669
0,909905567
14,359522419103900
4,715343849
7
0,904265341
0,896648294
14,273894939963900
4,588117156
8
0,891210499
0,884368998
14,192768112137200
4,467486611
9
0,878869537
0,872030350
14,115817843495700
4,352565782
10
0,866628626
0,860230552
14,042753034754000
4,242801681
11
0,854831609
0,848589700
13,973308662686200
4,137814211
12
0,843250897
0,837314037
13,907242987828300
4,037283606
13
0,832001542
0,826261206
13,844334505896600
3,940936337
14
0,820995553
0,815497743
13,784380045189000
3,848521743
15
0,810266979
0,804966957
13,727192808899800
3,759812059
16
0,799778396
0,794686358
13,672600853099300
3,674595835
17
0,789535800
0,784630345
13,620445636362400
3,592677880
18
0,779520366
0,774799711
13,570580790710000
3,513876598
19
0,769728817
0,765180416
13,522870992857600
3,438023378
20
0,760149472
0,755767918
13,477190974079800
3,364961115
21
0,750776352
0,746552749
13,433424623226000
3,294543452
22
0,741600798
0,737528983
13,391464187766000
3,226633778
23
0,732616368
0,728689198
13,351209552529500
3,161104506
24
0,723815911
0,720027406
13,312567592195300
3,097836320
25
0,715193248
0,711537292
13,275451586431100
3,036717546
945
0,000426015
0,000426015
12,000000362977700
0,001204953
946
0,000422687
0,000422687
12,000000357328300
0,001195539
947
0,000419385
0,000419385
12,000000351766900
0,001186199
948
0,000416108
0,000416108
12,000000346292000
0,001176932
949
0,000412857
0,000412857
12,000000340902300
0,001167737
950
0,000409632
0,000409632
12,000000335596500
0,001158614
951
0,000406432
0,000406432
12,000000330373300
0,001149562
952
0,000403256
0,000403256
12,000000325231400
0,001140581
953
0,000400106
0,000400106
12,000000320169500
0,001131671
954
0,000396980
0,000396980
12,000000315186400
0,001122829
955
0,000393879
0,000393879
12,000000310280800
0,001114057
956
0,000390801
0,000390801
12,000000305451600
0,001105354
957
0,000387748
0,000387748
12,000000300697600
0,001096718
958
0,000384719
0,000384719
12,000000296017600
0,001088150
959
0,000381713
0,000381713
12,000000291410300
0,001079649
960
0,000378731
0,000378731
12,000000286874800
0,001071214
961
0,000375772
0,000375772
12,000000282409900
0,001062845
962
0,000372837
0,000372837
12,000000278014500
0,001054542
963
0,000369924
0,000369924
12,000000273687500
0,001046303
964
0,000367034
0,000367034
12,000000269427800
0,001038129
965
0,000364166
0,000364166
12,000000265234500
0,001030018
966
0,000361321
0,000361321
12,000000261106400
0,001021971
967
0,000358499
0,000358499
12,000000257042500
0,001013987
968
0,000355698
0,000355698
12,000000253041900
0,001006066
969
0,000352919
0,000352919
12,000000249103600
0,000998206
Таблица 5.11 – Реализация градиентного метода при 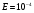
Номер итерации
Х1
Х2
Функция
Параметр останова
1
0,992187500
0,976562500
14,872248322711100
5,725771436
2
0,972112596
0,966700991
14,755778561425900
5,391343315
3
0,960252606
0,949298075
14,647453457158200
5,170831157
4
0,944120479
0,937143394
14,545808827169400
4,999364954
5
0,931250704
0,922455245
14,450015755630300
4,851038521
6
0,917052669
0,909905567
14,359522419103900
4,715343849
7
0,904265341
0,896648294
14,273894939963900
4,588117156
8
0,891210499
0,884368998
14,192768112137200
4,467486611
9
0,878869537
0,872030350
14,115817843495700
4,352565782
10
0,866628626
0,860230552
14,042753034754000
4,242801681
11
0,854831609
0,848589700
13,973308662686200
4,137814211
12
0,843250897
0,837314037
13,907242987828300
4,037283606
13
0,832001542
0,826261206
13,844334505896600
3,940936337
14
0,820995553
0,815497743
13,784380045189000
3,848521743
15
0,810266979
0,804966957
13,727192808899800
3,759812059
16
0,799778396
0,794686358
13,672600853099300
3,674595835
17
0,789535800
0,784630345
13,620445636362400
3,592677880
18
0,779520366
0,774799711
13,570580790710000
3,513876598
19
0,769728817
0,765180416
13,522870992857600
3,438023378
20
0,760149472
0,755767918
13,477190974079800
3,364961115
21
0,750776352
0,746552749
13,433424623226000
3,294543452
22
0,741600798
0,737528983
13,391464187766000
3,226633778
23
0,732616368
0,728689198
13,351209552529500
3,161104506
24
0,723815911
0,720027406
13,312567592195300
3,097836320
25
0,715193248
0,711537292
13,275451586431100
3,036717546
1239
0,000042461
0,000042461
12,000000003605800
0,000120097
1240
0,000042129
0,000042129
12,000000003549700
0,000119159
1241
0,000041800
0,000041800
12,000000003494500
0,000118228
1242
0,000041473
0,000041473
12,000000003440100
0,000117304
1243
0,000041149
0,000041149
12,000000003386500
0,000116388
1244
0,000040828
0,000040828
12,000000003333800
0,000115479
1245
0,000040509
0,000040509
12,000000003281900
0,000114576
1246
0,000040192
0,000040192
12,000000003230900
0,000113681
1247
0,000039878
0,000039878
12,000000003180600
0,000112793
1248
0,000039567
0,000039567
12,000000003131100
0,000111912
1249
0,000039258
0,000039258
12,000000003082300
0,000111038
1250
0,000038951
0,000038951
12,000000003034400
0,000110170
1251
0,000038647
0,000038647
12,000000002987100
0,000109309
1252
0,000038345
0,000038345
12,000000002940600
0,000108455
1253
0,000038045
0,000038045
12,000000002894900
0,000107608
1254
0,000037748
0,000037748
12,000000002849800
0,000106767
1255
0,000037453
0,000037453
12,000000002805500
0,000105933
1256
0,000037161
0,000037161
12,000000002761800
0,000105106
1257
0,000036870
0,000036870
12,000000002718800
0,000104285
1258
0,000036582
0,000036582
12,000000002676500
0,000103470
1259
0,000036296
0,000036296
12,000000002634800
0,000102662
1260
0,000036013
0,000036013
12,000000002593800
0,000101860
1261
0,000035731
0,000035731
12,000000002553500
0,000101064
1262
0,000035452
0,000035452
12,000000002513700
0,000100274
1263
0,000035175
0,000035175
12,000000002474600
0,000099491
Таблица 5.12 – Реализация градиентного метода при 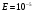
Номер итерации
Х1
Х2
Функция
Параметр останова
1
0,992187500
0,976562500
14,872248322711100
5,725771436
2
0,972112596
0,966700991
14,755778561425900
5,391343315
3
0,960252606
0,949298075
14,647453457158200
5,170831157
4
0,944120479
0,937143394
14,545808827169400
4,999364954
5
0,931250704
0,922455245
14,450015755630300
4,851038521
6
0,917052669
0,909905567
14,359522419103900
4,715343849
7
0,904265341
0,896648294
14,273894939963900
4,588117156
8
0,891210499
0,884368998
14,192768112137200
4,467486611
9
0,878869537
0,872030350
14,115817843495700
4,352565782
10
0,866628626
0,860230552
14,042753034754000
4,242801681
11
0,854831609
0,848589700
13,973308662686200
4,137814211
12
0,843250897
0,837314037
13,907242987828300
4,037283606
13
0,832001542
0,826261206
13,844334505896600
3,940936337
14
0,820995553
0,815497743
13,784380045189000
3,848521743
15
0,810266979
0,804966957
13,727192808899800
3,759812059
16
0,799778396
0,794686358
13,672600853099300
3,674595835
17
0,789535800
0,784630345
13,620445636362400
3,592677880
18
0,779520366
0,774799711
13,570580790710000
3,513876598
19
0,769728817
0,765180416
13,522870992857600
3,438023378
20
0,760149472
0,755767918
13,477190974079800
3,364961115
21
0,750776352
0,746552749
13,433424623226000
3,294543452
22
0,741600798
0,737528983
13,391464187766000
3,226633778
23
0,732616368
0,728689198
13,351209552529500
3,161104506
24
0,723815911
0,720027406
13,312567592195300
3,097836320
25
0,715193248
0,711537292
13,275451586431100
3,036717546
1532
0,000004265
0,000004265
12,000000000036400
0,000012064
1533
0,000004232
0,000004232
12,000000000035800
0,000011970
1534
0,000004199
0,000004199
12,000000000035300
0,000011877
1535
0,000004166
0,000004166
12,000000000034700
0,000011784
1536
0,000004134
0,000004134
12,000000000034200
0,000011692
1537
0,000004101
0,000004101
12,000000000033600
0,000011600
1538
0,000004069
0,000004069
12,000000000033100
0,000011510
1539
0,000004038
0,000004038
12,000000000032600
0,000011420
1540
0,000004006
0,000004006
12,000000000032100
0,000011331
1541
0,000003975
0,000003975
12,000000000031600
0,000011242
1542
0,000003944
0,000003944
12,000000000031100
0,000011154
1543
0,000003913
0,000003913
12,000000000030600
0,000011067
1544
0,000003882
0,000003882
12,000000000030100
0,000010981
1545
0,000003852
0,000003852
12,000000000029700
0,000010895
1546
0,000003822
0,000003822
12,000000000029200
0,000010810
1547
0,000003792
0,000003792
12,000000000028800
0,000010725
1548
0,000003762
0,000003762
12,000000000028300
0,000010641
1549
0,000003733
0,000003733
12,000000000027900
0,000010558
1550
0,000003704
0,000003704
12,000000000027400
0,000010476
1551
0,000003675
0,000003675
12,000000000027000
0,000010394
1552
0,000003646
0,000003646
12,000000000026600
0,000010313
1553
0,000003618
0,000003618
12,000000000026200
0,000010232
1554
0,000003589
0,000003589
12,000000000025800
0,000010152
1555
0,000003561
0,000003561
12,000000000025400
0,000010073
1556
0,000003534
0,000003534
12,000000000025000
0,000009994
Таблица 5.13– Реализация градиентного метода при 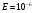
Номер итерации
Х1
Х2
Функция
Параметр останова
1
0,992187500
0,976562500
14,872248322711100
5,725771436
2
0,972112596
0,966700991
14,755778561425900
5,391343315
3
0,960252606
0,949298075
14,647453457158200
5,170831157
4
0,944120479
0,937143394
14,545808827169400
4,999364954
5
0,931250704
0,922455245
14,450015755630300
4,851038521
6
0,917052669
0,909905567
14,359522419103900
4,715343849
7
0,904265341
0,896648294
14,273894939963900
4,588117156
8
0,891210499
0,884368998
14,192768112137200
4,467486611
9
0,878869537
0,872030350
14,115817843495700
4,352565782
10
0,866628626
0,860230552
14,042753034754000
4,242801681
11
0,854831609
0,848589700
13,973308662686200
4,137814211
12
0,843250897
0,837314037
13,907242987828300
4,037283606
13
0,832001542
0,826261206
13,844334505896600
3,940936337
14
0,820995553
0,815497743
13,784380045189000
3,848521743
15
0,810266979
0,804966957
13,727192808899800
3,759812059
16
0,799778396
0,794686358
13,672600853099300
3,674595835
17
0,789535800
0,784630345
13,620445636362400
3,592677880
18
0,779520366
0,774799711
13,570580790710000
3,513876598
19
0,769728817
0,765180416
13,522870992857600
3,438023378
20
0,760149472
0,755767918
13,477190974079800
3,364961115
21
0,750776352
0,746552749
13,433424623226000
3,294543452
22
0,741600798
0,737528983
13,391464187766000
3,226633778
23
0,732616368
0,728689198
13,351209552529500
3,161104506
24
0,723815911
0,720027406
13,312567592195300
3,097836320
25
0,715193248
0,711537292
13,275451586431100
3,036717546
1826
0,000000425
0,000000425
12,000000000000400
0,000001202
1827
0,000000422
0,000000422
12,000000000000400
0,000001193
1828
0,000000419
0,000000419
12,000000000000400
0,000001184
1829
0,000000415
0,000000415
12,000000000000300
0,000001174
1830
0,000000412
0,000000412
12,000000000000300
0,000001165
1831
0,000000409
0,000000409
12,000000000000300
0,000001156
1832
0,000000406
0,000000406
12,000000000000300
0,000001147
1833
0,000000402
0,000000402
12,000000000000300
0,000001138
1834
0,000000399
0,000000399
12,000000000000300
0,000001129
1835
0,000000396
0,000000396
12,000000000000300
0,000001120
1836
0,000000393
0,000000393
12,000000000000300
0,000001112
1837
0,000000390
0,000000390
12,000000000000300
0,000001103
1838
0,000000387
0,000000387
12,000000000000300
0,000001094
1839
0,000000384
0,000000384
12,000000000000300
0,000001086
1840
0,000000381
0,000000381
12,000000000000300
0,000001077
1841
0,000000378
0,000000378
12,000000000000300
0,000001069
1842
0,000000375
0,000000375
12,000000000000300
0,000001061
1843
0,000000372
0,000000372
12,000000000000300
0,000001052
1844
0,000000369
0,000000369
12,000000000000300
0,000001044
1845
0,000000366
0,000000366
12,000000000000300
0,000001036
1846
0,000000363
0,000000363
12,000000000000300
0,000001028
1847
0,000000361
0,000000361
12,000000000000300
0,000001020
1848
0,000000358
0,000000358
12,000000000000300
0,000001012
1849
0,000000355
0,000000355
12,000000000000300
0,000001004
1850
0,000000352
0,000000352
12,000000000000200
0,000000996
Данные по количеству итераций и заданным точностям для градиентного метода сведены в таблицу 5.14
Таблица 5.14 - Зависимость числа итераций от точности
Точность
Количество итераций
0,1
382
0,01
676
0,001
969
0,0001
1263
0,00001
1556
0,000001
1850
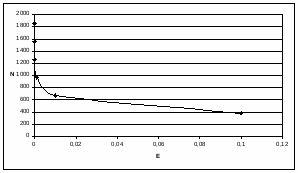
Рисунок 5.2 – Графическое представление зависимости количества итераций N от точности E для градиентного метода.
Таким образом, анализируя полученные зависимости можно сделать вывод о том, что метод Нелдера-Мида является более эффективным. Так же следует отметить, что градиентный метод быстро приближается к экстремуму, когда текущая точка находится далеко от него, и резко замедляется вблизи экстремума.
Следует заметить, что эффективность применения методов оптимизации прежде всего обусловлена видом функции.
6. ЗАКЛЮЧЕНИЕ
В курсовой работе произведена минимизации функции 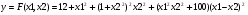 с помощью метода оптимизации нулевого порядка – метода Нелдера-Мида и метода оптимизации первого порядка – градиентного метода с дроблением шага.
с помощью метода оптимизации нулевого порядка – метода Нелдера-Мида и метода оптимизации первого порядка – градиентного метода с дроблением шага.
В результате решения задачи минимизации с помощью метода Нелдера-Мида получено следующее значение функции: 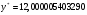 . Данный оптимум достигается в точке
. Данный оптимум достигается в точке 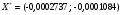 . Этот метод позволяет найти минимум (при начальной точке Х (1 ; 1)) за 29 итераций при точности решения
. Этот метод позволяет найти минимум (при начальной точке Х (1 ; 1)) за 29 итераций при точности решения 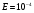 . При этом параметр останова равен 0,0000921.
. При этом параметр останова равен 0,0000921.
В результате реализации градиентного метода минимальное значение функции составляет 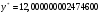 . Данный оптимум достигнут в точке
. Данный оптимум достигнут в точке 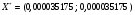 . Этот метод позволяет найти минимум (при начальной точке Х(1;1)) за 1263 итерации при точности решения
. Этот метод позволяет найти минимум (при начальной точке Х(1;1)) за 1263 итерации при точности решения 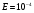 . При этом параметр останова равен 0,000099491.
. При этом параметр останова равен 0,000099491.
Для каждого из методов была установлена зависимость числа итераций от заданной точности . Анализируя полученные результаты, можно сделать вывод о том, что по числу итераций более эффективным является метод Нелдера-Мида. Однако следует отметить, что эффективность этих методов может изменяться в зависимости от выбора начального приближения и вида функции. Следует также учесть, что градиентный метод может быть непригоден в тех случаях, если расчет производных вызывает затруднение.
7. ПРИЛОЖЕНИЕ
В таблицах представлены координаты точек, образующих линии уровня
В настоящем приложении представлена реализация программного кода для каждого из методов оптимизации. Используемый язык программирования – Visual Studio C# 2005.
Градиентный метод с дроблением шага
namespace GradientL
{public partial class Form1 : Form
{public Form1()
{InitializeComponent();}
public static string[] str = new string[100000];
struct Tk
{public double x1, x2;
public Tk(double X, double Y)
{x1 = X;
x2 = Y;}
public static Tk operator /(Tk v1, double q)
{return new Tk(v1.x1 / q, v1.x2 / q);}
public static Tk operator *(Tk v, double d)
{return new Tk(v.x1 * d, v.x2 * d);}
public static Tk operator *(Tk v1, Tk v2)
{return new Tk(v1.x1 * v2.x1, v1.x2 * v2.x2);}
public static Tk operator -(Tk v1, Tk v2)
{return new Tk(v1.x1 - v2.x1, v1.x2 - v2.x2);}
public static Tk operator +(Tk v1, Tk v2)
{return new Tk(v1.x1 + v2.x1, v1.x2 + v2.x2);}
public static double Dist(Tk v1, Tk v2)
{return Math.Sqrt((v1.x1 - v2.x1) * (v1.x1 - v2.x1) + (v1.x2 - v2.x2) * (v1.x2 - v2.x2));}
public override string ToString()
{return "(" + this.x1.ToString("f5") + ";" + this.x2.ToString("f5") + ")";}}
class Pr
{public static double f(Tk c)
{return 12 + c.x1 * c.x1 + (1 + c.x2 * c.x2) * c.x2 * c.x2 + (c.x1 * c.x1 * c.x2 * c.x2 + 100) * (c.x1 - c.x2) * (c.x1 - c.x2);}
static Tk gradient(Tk c)
{Tk N = new Tk(2 * c.x1 + 2 * c.x1 * c.x2 * c.x2 *
( c.x1 - c.x2)*(c.x1 - c.x2) + 2 * (c.x1 * c.x1 * c.x2 * c.x2 + 100) * (c.x1 - c.x2),
2 * c.x2*c.x2*c.x2+2*c.x2*(1+c.x2*c.x2)+
2*c.x2*c.x1*c.x1*(c.x1-c.x2)*(c.x1-c.x2)-2*(c.x1-c.x2)*
(c.x1*c.x1*c.x2*c.x2+100));
return N;}
public static double Dl(Tk c)
{return Math.Sqrt(c.x1 * c.x1 + c.x2 * c.x2);}
public static void Tr(double eps, ref Tk ca, out double fn, out int i)
{Tk cb = new Tk(1, 1), st = new Tk(0.5, 0.5);
Tk step = new Tk(1, 1), eq; i = 0;
do
{while (true)
{cb = ca - step * gradient(ca);
eq = st * step * gradient(cb) * gradient(cb);
if (f(cb - step * gradient(cb)) >= (f(cb) - Dl(eq)))
{ step.x1 /= 2;
step.x2 /= 2;}
else break;}
fn = f(ca);
i++;
str[i] = String.Format("{0}" + ") " + "{1}" + "; " +
"{2}" + "; " + "{3}" + ".", i.ToString(), ca.ToString(), fn.ToString("f6"), Dl(gradient(cb)).ToString("f6"));
ca = cb;}
while (Dl(gradient(cb)) >= eps);
fn = f(cb);}}
private void button1_Click(object sender, EventArgs e)
{listBox1.Items.Clear();
double Et = Convert.ToDouble(textBox3.Text);
double fn;
int j;
Tk mas = new Tk(Convert.ToDouble(textBox1.Text), Convert.ToDouble(textBox2.Text));
Pr.Tr(Et, ref mas, out fn, out j);
Min.Visible = true;
Min.Text = String.Format("{0}" + "; " + "{1}" + "; " +
"{2}", mas.ToString(), fn.ToString(), j.ToString());
for (int i = 1; i < j; i++)
listBox1.Items.Add(str[i]);}
private void Form1_Load(object sender, EventArgs e){}}}
Метод Нелдера-Мида
namespace Nelder_Method
{public partial class Form1 : Form
{public Form1()
{InitializeComponent();}
static double Al = 1.0;
static double Bt = 0.5;
static double Gm = 2.0;
static int n=0;
static string[] op = new string[1000];
const int cap = 2;
struct Tk
{public double x1, x2;
public Tk(double X, double Y)
{x1 = X;
x2 = Y;}
public static Tk operator /(Tk v1, double q)
{return new Tk(v1.x1 / q, v1.x2 / q);}
public static Tk operator *(Tk v, double d)
{return new Tk(v.x1 * d, v.x2 * d);}
public static Tk operator *(Tk v1, Tk v2)
{return new Tk(v1.x1 * v2.x1, v1.x2 * v2.x2);}
public static Tk operator -(Tk v1, Tk v2)
{return new Tk(v1.x1 - v2.x1, v1.x2 - v2.x2);}
public static Tk operator +(Tk v1, Tk v2)
{return new Tk(v1.x1 + v2.x1, v1.x2 + v2.x2);}
public static double Dist(Tk v1, Tk v2)
{return Math.Sqrt((v1.x1 - v2.x1) * (v1.x1 - v2.x1) + (v1.x2 - v2.x2) * (v1.x2 - v2.x2));}
public override string ToString()
{return "(" + this.x1.ToString("f5") + ";" + this.x2.ToString("f5") + ")";}}
class Cnt
{public static double function(Tk c)
{return 12 + c.x1*c.x1 + (1+c.x2*c.x2)*c.x2*c.x2 + (c.x1*c.x1*c.x2*c.x2+100)*(c.x1-c.x2)*(c.x1-c.x2);}
public static void Pr(ref Tk[] c, ref double[] ot)
{double fir; Tk tk;
for (int k = 1; k <= cap; k++)
for (int l = k; l >= 1; l--)
if (ot[l - 1] > ot[l])
{fir = ot[l];
tk = c[l];
ot[l] = ot[l - 1];
c[l] = c[l - 1];
ot[l - 1] = fir;
c[l - 1] = tk;}
else break;}
public static bool Ostanov(Tk[] w, double E, double n, Tk c, out double Ost)
{double Lp;
double d = 0.5;
double p1 = 0;
Tk p2 = new Tk(0, 0);
for (int i = 0; i <= cap; i++)
{p1 += (function(w[i]) - function(c)) * (function(w[i]) - function(c));
p2 += (w[i] - c) * (w[i] - c);}
Lp = Math.Sqrt(p2.x1 * p2.x1 + p2.x2 * p2.x2);
Ost = d * (Math.Sqrt((1 / (n + 1)) * p1)) + (1 - d) * (Math.Sqrt((1 / (n + 1)) * Lp));
if (Ost < E)
return true;
else return false;}
public static double Met(Tk[] c, double tchn)
{double[] f = new double[cap + 1];
double val1=0, val2=0, val3 = 0, val4, val5, val6, val7;
Tk sim1, sim2, sim3, sim4, sim5, sim6, sim_cen, sim7;
sim_cen.x1 = sim_cen.x2 = 0;
int i;
double J1;
bool flag;
for (i = 0; i <= cap; i++) // Вычисление значений функции на начальном симплексе
f[i] = function(c[i]);
while (!Ostanov(c, tchn, n, sim_cen, out J1))// Проверка на условие выхода
{n++;
// Шаг 1. Сортировка
Pr(ref c, ref f);
sim1 = c[cap]; val1 = f[cap];
sim2 = c[cap - 1]; val2 = f[cap - 1];
sim3 = c[0]; val3 = f[0];
// Шаг 2. Вычисление центра тяжести симплекса
sim_cen.x1 = sim_cen.x2 = 0;
for (i = 0; i < cap; i++)
sim_cen = sim_cen + c[i];
sim_cen = sim_cen / cap;
// 3Шаг . Отражение
sim4 = sim_cen * (1 + Al) - sim1 * Al; val4 = function(sim4);
// Шаг 4.
if (val4 <= val3)
{ // Шаг 4a.
sim5 = sim_cen * (1 - Gm) + sim4 * Gm;
val5 = function(sim5);
if (val5 < val3)
{c[cap] = sim5;
f[cap] = val5;}
else
{c[cap] = sim4;
f[cap] = val4;}}
if ((val3 < val4) && (val4 <= val2))
{ // Шаг 4.b
c[cap] = sim4;
f[cap] = val4;}
flag = false;
if ((val1 >= val4) && (val4 > val2))
{ // Шаг 4c.
flag = true;
val7 = val1;
sim7 = sim1;
c[cap] = sim4;
f[cap] = val4;
sim4 = sim7;
val4 = val7;}
// Шаг 4d.
if (val4 > val1) flag = true;
if (flag)
{ // Шаг 5. Сжатие
sim6 = sim1 * Bt + sim_cen * (1 - Bt);
val6 = function(sim6);
if (val6 < val1)
{ // Шаг 6.
val7 = val1;
sim7 = sim1;
c[cap] = sim6;
f[cap] = val6;
sim6 = sim7;
val6 = val7;}
else
{ // Шаг 7. Глобальное сжатие
for (i = 0; i <= cap; i++)
c[i] = sim3 + (c[i] - sim3) / 2;}}
op[n - 1] = Convert.ToString(n) + "; " + sim1.ToString() +
"; " + sim2.ToString() + "; " + sim3.ToString();}
return (val3 + val1 + val2) / 3;}}
private void button1_Click(object sender, EventArgs e)
{Tk ta = new Tk(0, 0);
Tk tb = new Tk(0.26, 0.96);
Tk tc = new Tk(0.96, 0.26);
Tk[] t = new Tk[3] { ta, tb, tc };
listBox1.Items.Clear();
n = 0;
op = new string[200];
double eps1 = Convert.ToDouble(textBox2.Text);
label4.Text = Cnt.Met(t, eps1).ToString("f5") + "; " + Convert.ToString(n) + ".";
for (int i = 0; i < n; i++)
listBox1.Items.Add(op[i]);}
private void Form1_Load(object sender, EventArgs e){}}
8. СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ
Агуров П.В. C# в подлиннике (программирование на языке С#) – Петербург, 2006
Агуров П.В. Сборник рецептов по C# - Петербург,2006
Банди Б. Методы оптимизации – Москва, 1988
Базара М, Шетти К. Нелинейное программироваине. Теория и алгоритмы – М.:Мир, 1988
Поляк Б.Т. Введение в оптимизацию. - М.: Наука, 1983
Раскин Л.Г. Математическое программирование: Учебное пособие – Харьков: НТУ «ХПИ» , 2002
Рихтер Д. Программирование на платформе Microsoft. NET Freamework для профессионалов – М.Microsoft Press, 2003
Серая О.В. Методические указания для проведения лабораторных работ по курсу «Математическое программирование» - Харьков: НТУ «ХПИ» , 2003
Сухарев А.Г., Тимохов А.В Курс методов оптимизации – М.: Наука, 1986
Химмельблау Д. Прикладное нелинейное программирование М.:Мир, 1989

Нравится материал? Поддержи автора!
Ещё документы из категории информатика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ