Тема урока «Моделирование геометрических операций и фигур»

9 класс

Учитель информатики и математики

МАОУ «Средней общеобразовательной школы №14» г. Владимира

Грехова Екатерина Александровна

Комментарий к уроку

Интерактивная доска прочно вошла в мою повседневную школьную жизнь с первых дней появления в кабинете информатики.

Во-первых, она позволяет существенно экономить время на различных этапах урока.

Во-вторых, интерактивная доска дает возможность многократно использовать подготовленный материал: при объяснении нового материала, при проверке домашнего задания и тематическом повторении.

Интерактивная доска обладает уникальной возможностью сочетать вывод на нее любой информации с компьютера с произвольным дополнением выведенного изображения подчеркиваниями, комментариями.

На занятии с интерактивной доской можно использовать все материалы, доступные на компьютере: таблицы, схемы, анимацию, аудио- и видео-записи. Разнообразие этих ресурсов предоставляет широкий выбор подходов к обучению.

Интерактивная доска позволяет учителю «открыть» часть информации, а другую часть оставить скрытой, что очень удобно при дифференцированной работе с последующей проверкой.

Интерактивная доска усиливает интерес к изучаемому материалу, что является необходимым условием успешности обучения.

Следуя САНПИНам, использовать интерактивную доску на уроке рекомендуется не более 10-15 минут. Поэтому нужно заранее определиться, какой прием, на каком уроке будет работать эффективнее.

Предлагаю вашему вниманию урок по теме «Моделирование геометрических операций и фигур» в 9 классе с разными приемами использования интерактивной доски. Тема «Моделирование» очень сжато представлена в задачнике по моделированию Макаровой Н.В., а в стандартах второго поколения она присутствует. Я предлагаю Вашему вниманию, как можно используя интерактивную доску наглядно показать учащимся алгоритмы моделирования геометрических операций и фигур.

Задания для урока созданы в программах SMART Notebook 10.

Тема: Моделирование геометрических операций и фигур

Класс: 9

Цель: Сформировать знания учащихся о геометрических моделях в жизни человека. Познакомить с алгоритмами построения основных геометрических операций. Сформировать навыки построения геометрических моделей в графическом редакторе.

Задачи:

Образовательные

• формирование навыков работы с программным обеспечением;

• выбор определённого программного средства для реализации, поставленной задачи;

• выработка умений и навыков решения практических задач в соответствующих программах.

Развивающие

• развитие внимания, способности к анализу;

• развитие логического мышления;

• развитие способностей к определённым видам деятельности (дизайн, инженерная графика, программирование и т.д.)

Воспитательные

• формирование самостоятельности мышления, чёткости и организованности в работе, умения контролировать свою деятельность;

• работать эффективно в соответствии с располагаемым временем.

Тип урока: комбинированный

Необходимое оборудование: компьютеры, интерактивная доска с программным обеспечением, проектор.

План урока:

1. Организационный момент 2 минуты

2. Постановка целей и задач урока 2 минуты

3. Актуализация знаний 7 минут

4. Объяснение нового материала 10 минут

5. Практическая работа 15 минут

6. Подведение итогов 2 минуты

7. Постановка домашнего задания 2 минуты

Ход урока:

1. Организационный момент

2. Постановка целей и задач урока

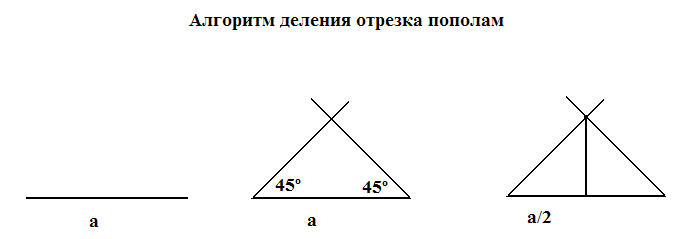
Сегодня на уроке мы узнаем, как можно делить отрезок, имея линейку без шкалы и циркуль, а также как разделить угол пополам, не имея транспортира.

3. Актуализация знаний

1. Соедините фразы.

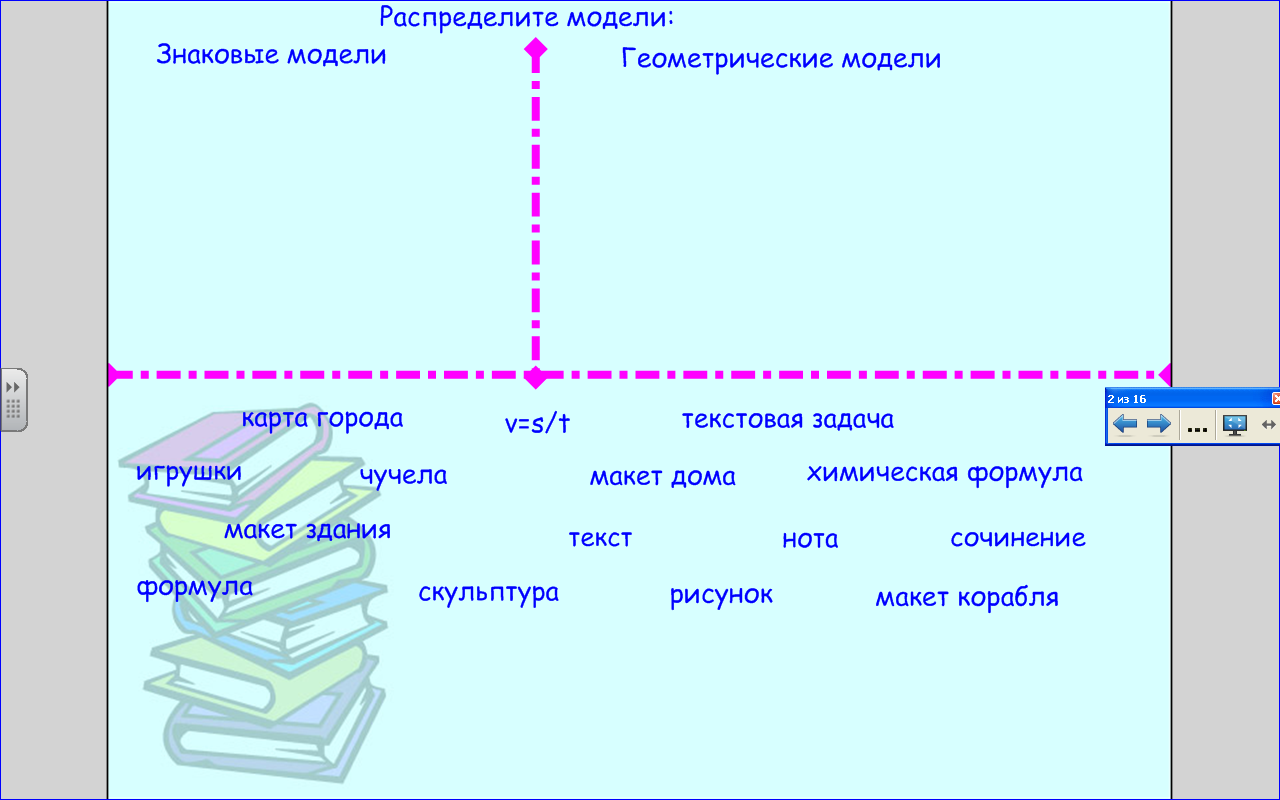
2. Распределите все модели по классам: знаковые и геометрические

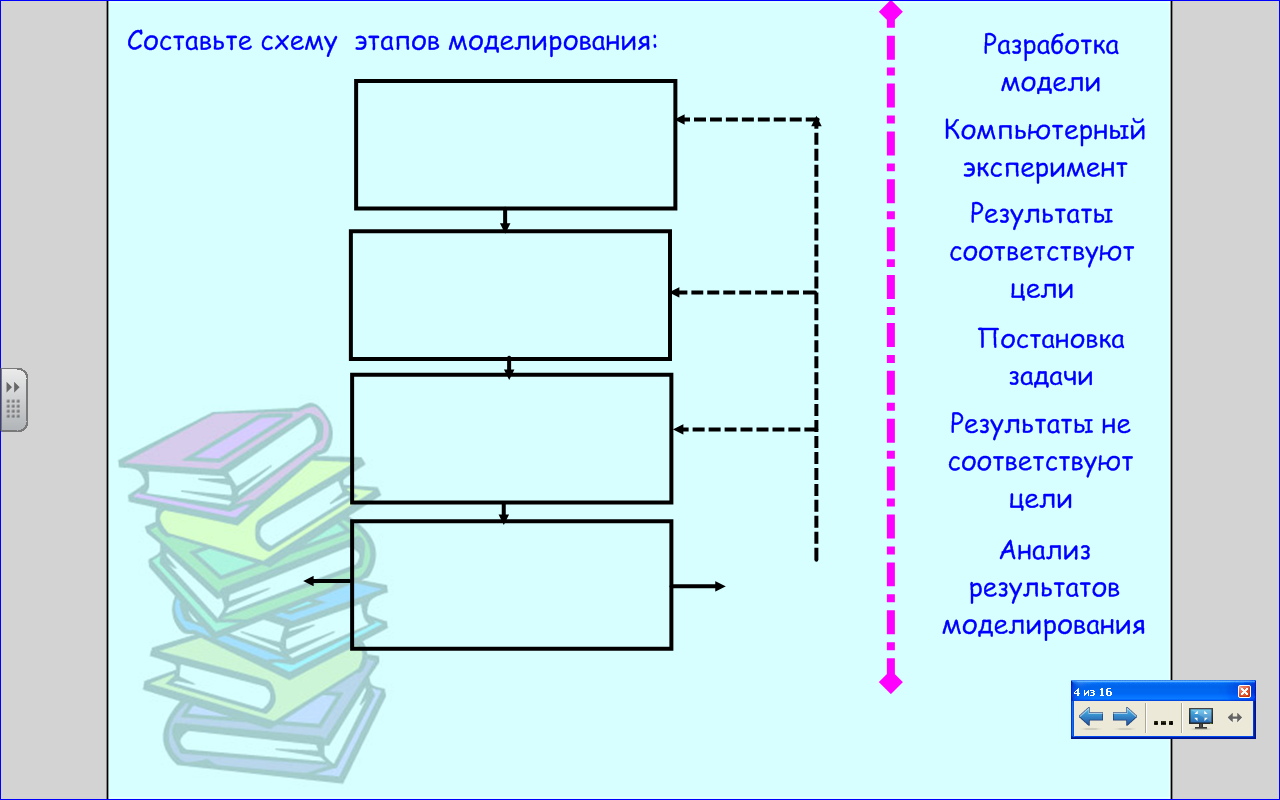
3. Составьте схему этапов моделирования

4. Объяснение нового материала

Задача 1. Построение геометрических операций.

• I этап. Постановка задачи.

Описание задачи.

Вся история геометрии связана с практикой построения при помощи подручных средств для измерения недоступного. В Древнем Египте, задолго до доказательства теоремы Пифагора, пользовались треугольником со сторонами, относящимися как 3:4:5 для получения прямых углов в треугольнике.

Фалес Милетский в VI в. до н.э. использовал метод измерения расстояния до кораблей, находящихся в море, с использованием признаков подобия треугольников.

Пифаго́р Само́сский (580 —500гг. до н. э.) — древнегреческий философ, поэт, астроном и математик. Создатель религиозно-философской школы пифагорейцев. Считал принципом мирового устройства Числа и их соотношения.

Историю жизни Пифагора трудно отделить от легенд, представляющих его в качестве совершенного мудреца и великого посвящённого во все таинства греков и варваров. Ещё Геродот называл его «величайшим эллинским мудрецом».

Самые ранние известные источники об учении Пифагора появились лишь 200 лет спустя после его смерти. Сам Пифагор не оставил сочинений, и все сведения о нём и его учении основываются на трудах его последователей, не всегда беспристрастных.

В честь Пифагора назван кратер на Луне.

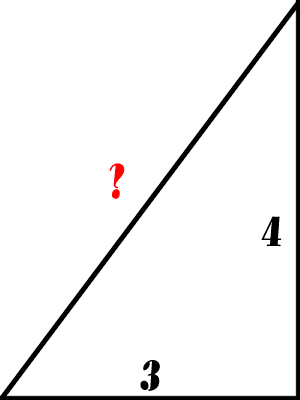
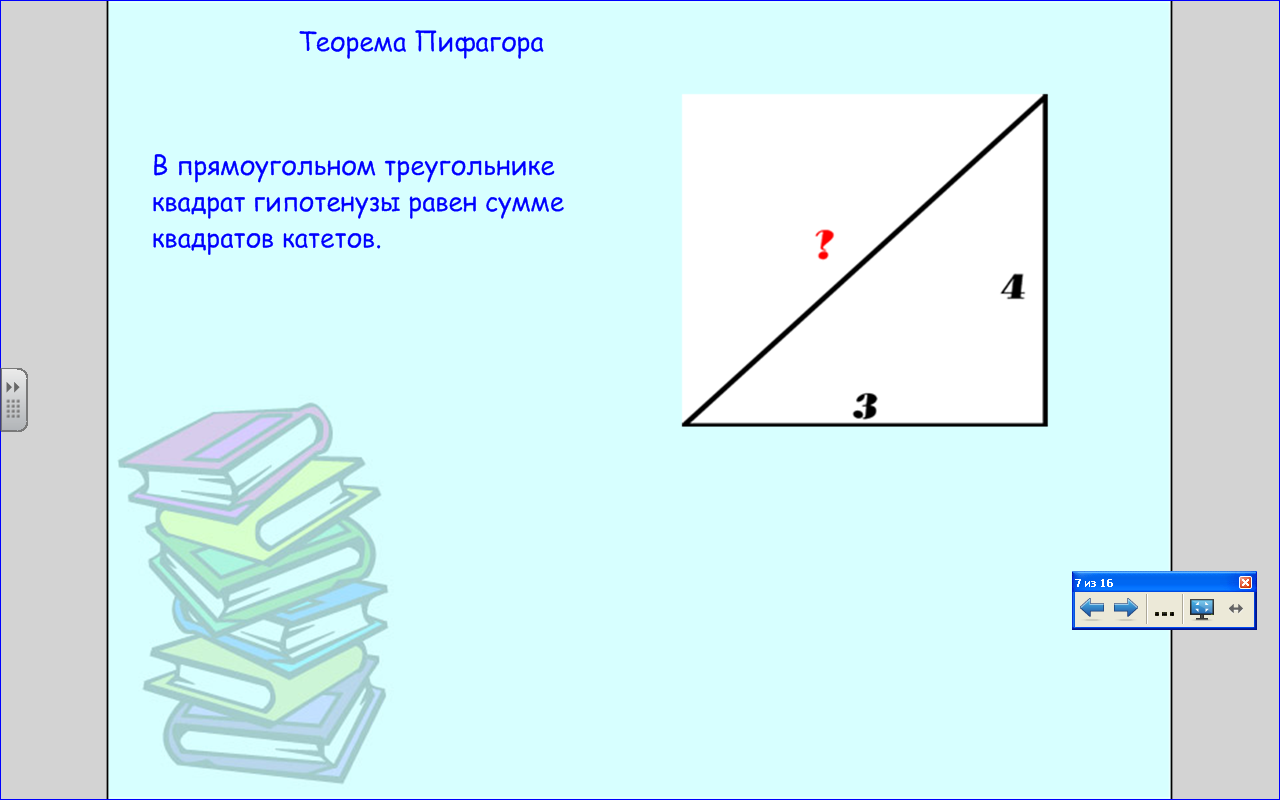
Теорема Пифагора

Фалес Милетский

Фале́с (640/624 — 548/545 до н. э.) — древнегреческий философ и математик из Милета (Малая Азия). Представитель ионической натурфилософии и основатель милетской (ионийской) школы, с которой начинается история европейской науки. Традиционно считается основоположником греческой философии (и науки) — он неизменно открывал список «семи мудрецов», заложивших основы греческой культуры и государственности.

Посмотрим, как ученые делили отрезки пополам и как проводили биссектрису угла.

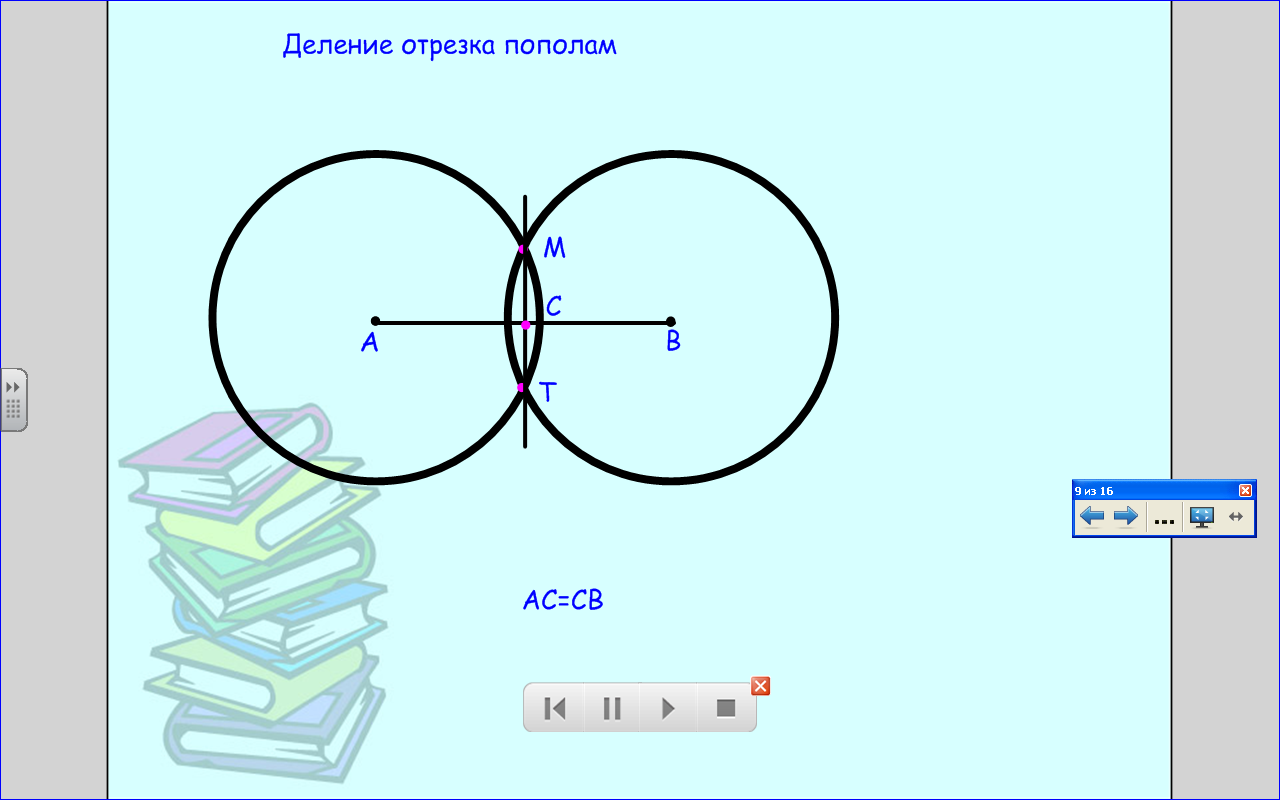
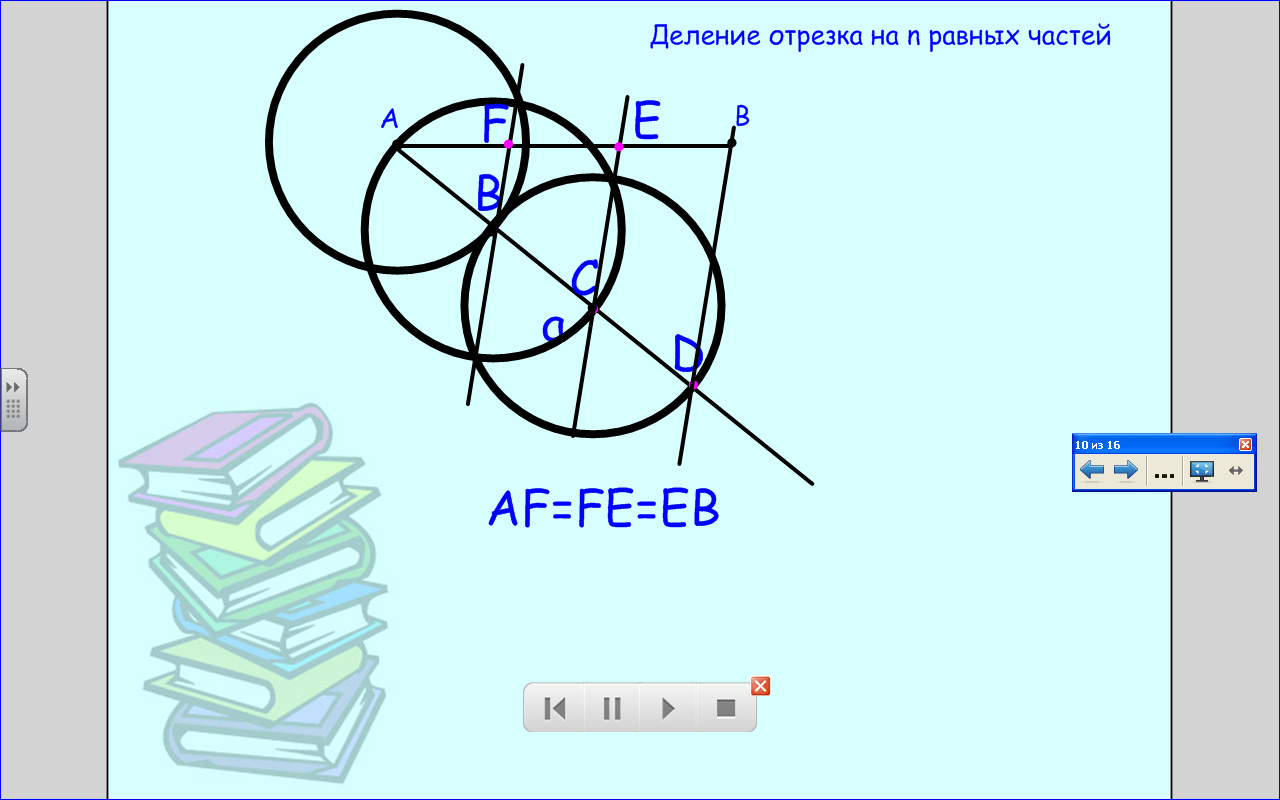
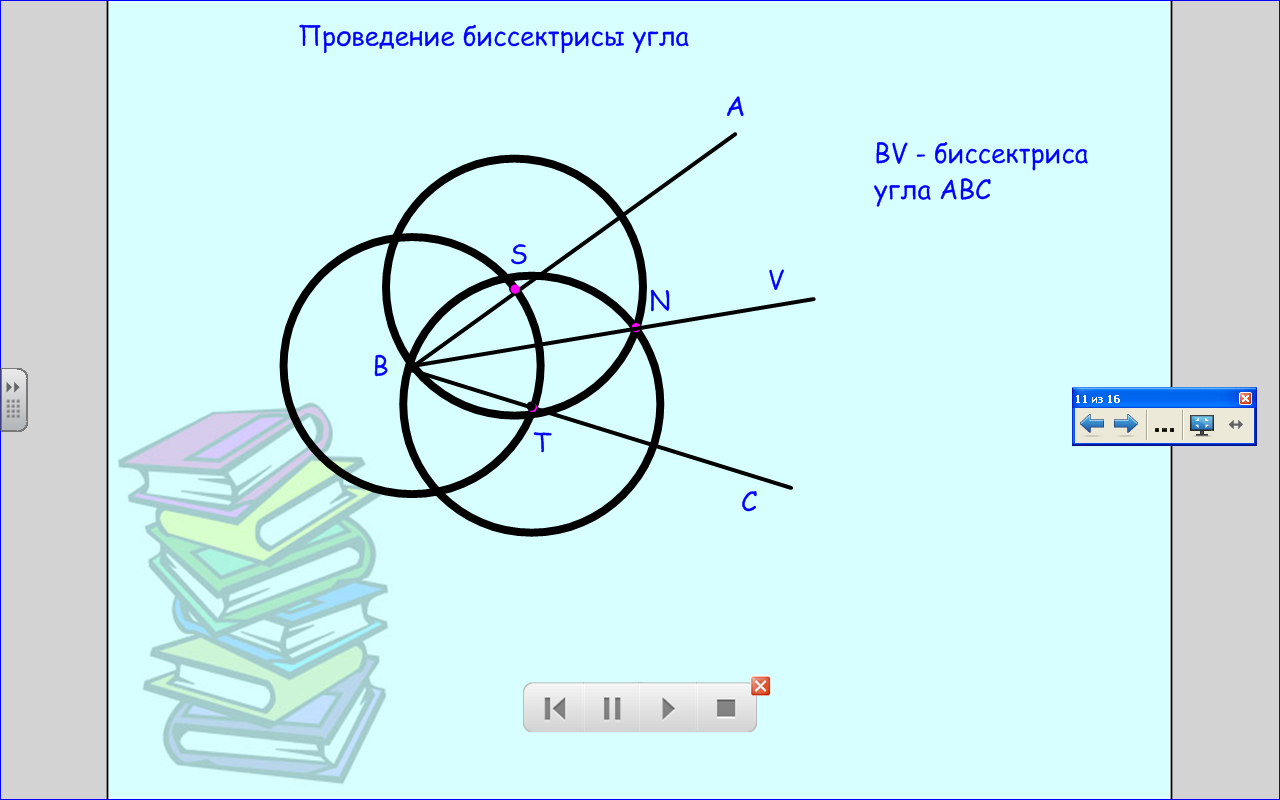
Цели моделирования.

При отсутствии специальных инструментов (линейки, транспортира, циркуля) смоделировать основные геометрические операции.

Формализация задачи.

Исходные геометрические объекты (отрезок, радиус, угол) задаются в левом верхнем углу рабочего поля. Для построения используются их копии. Построение основывается на законах геометрии.

• I I этап. Разработка модели.

Модель 1. Деление отрезков (моделирование функций линейки).

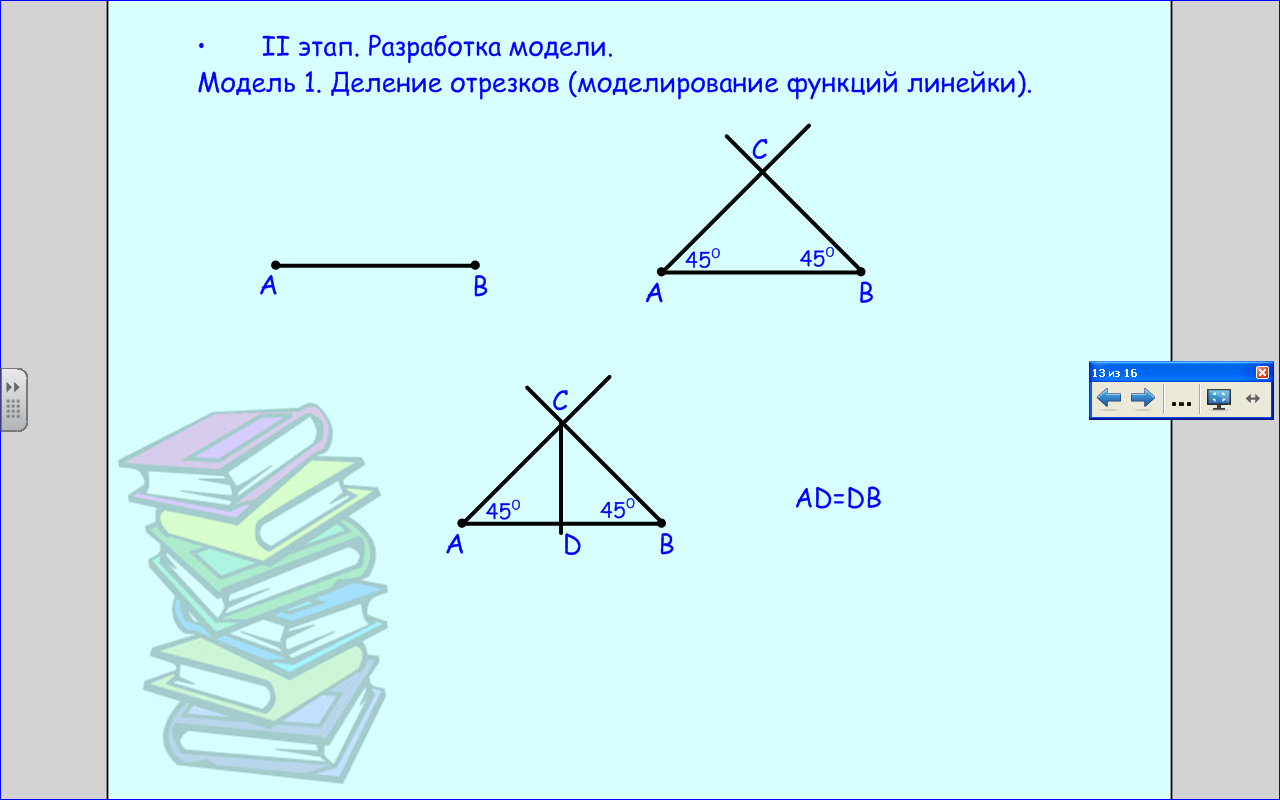
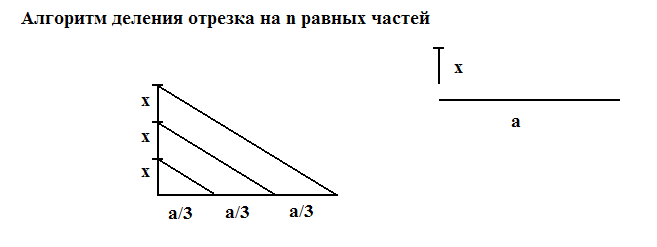
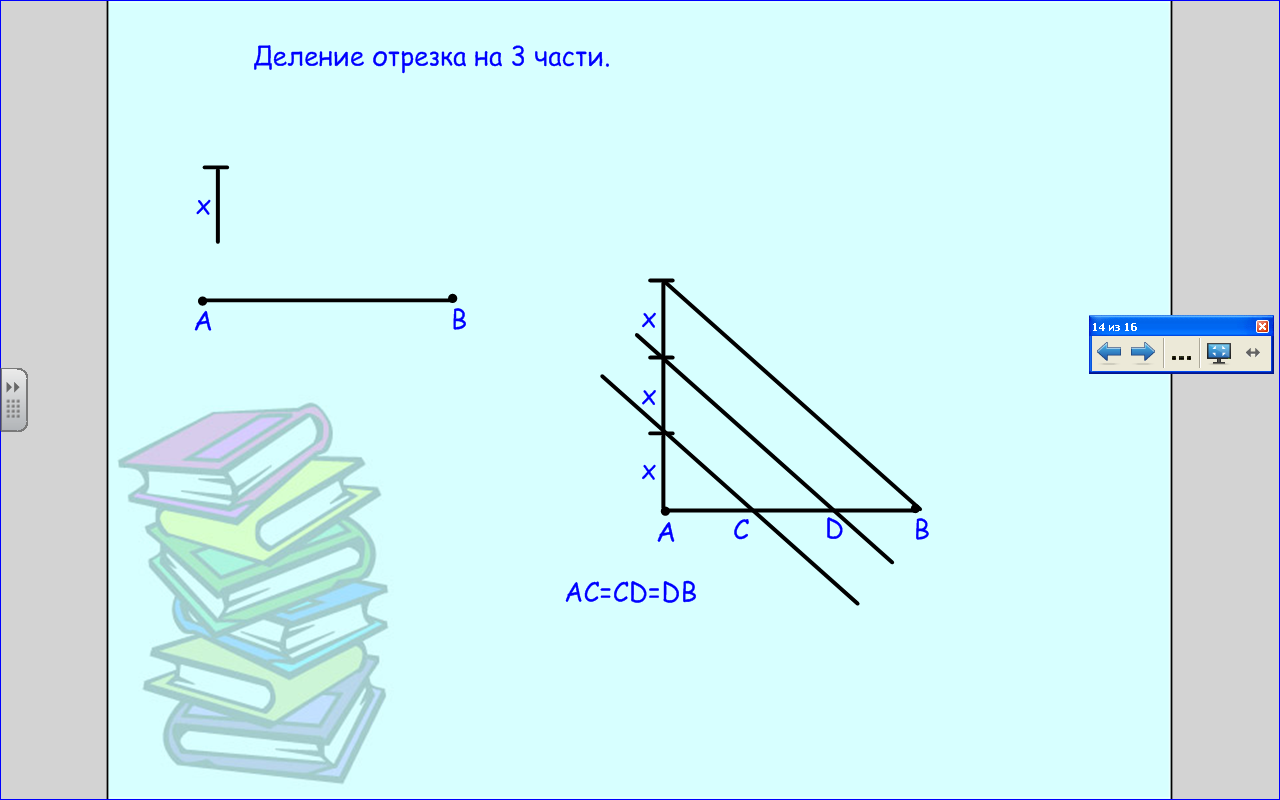
Модель 3. Деление угла пополам (моделирование функций транспортира).

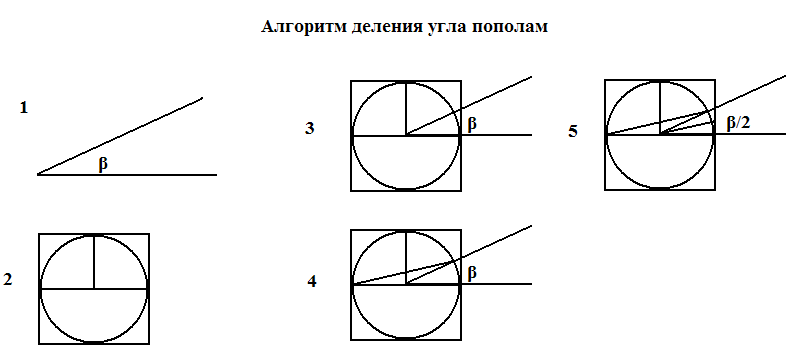
I I I этап. Компьютерный эксперимент.

План эксперимента.

1. Тестирование построенной по заданному алгоритму модели 1 совмещением отрезков, полученных при делении.

2. Тестирование построенной по заданному алгоритму модели 2 совмещением исходного и повернутого на 90º отрезка с радиусами полученной окружности.

Проведение исследования.

Доказать правильность алгоритмов построения.

• I V этап. Анализ результатов.

Если результаты тестирования отрицательные, увеличить точность выполнения алгоритма за счет работы в увеличенном масштабе.

5. Практическая работа

Построить модели 1, 2, 3 в графическом редакторе Paint.

6. Подведение итогов. Выставление оценок в журнал.

7. Постановка домашнего задания. Придумать алгоритм построения равностороннего треугольника в графическом редакторе Paint.