11

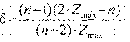
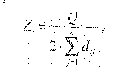
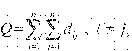
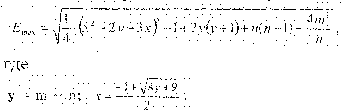
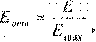
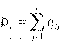
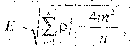
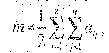
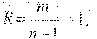
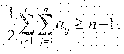
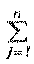
Федеральное агентство образования Российской Федерации

ГОУВПО «Воронежский Государственный Технический Университет»

Кафедра экономики, производственного менеджмента и

организации машиностроительного производства

КОНТРОЛЬНАЯ РАБОТА

по дисциплине «Методы моделирования производственных систем»

Воронеж 2008

Задание на выполнение домашней работы №1

По дисциплине «Методы моделирования производственных систем»

Теоретическая часть.

При использовании дополнительной литературы и материалов учебного пособия, в реферативной форме раскрыть следующие положения:

1. Методы и принципы системного анализа в их применении к решению управленческих проблем

2. Современная концепция математического моделирования

3. Виды и формы современного моделирования.

4. Методы статистического и имитационного моделирования.

5. Модели экономических систем.

6. Современные производственные системы и методы их формализации.

7. Концепция адекватности математических моделей.

8. Вероятностный подход к моделированию производственных систем.

9. Модель и объекты моделирования.

10. Методология моделирования производственных систем

Практическая часть

В рамках практического задания выполнить:

1. Разработать блок-схему модели СМО

2. Провести процесс моделирования.

3. Построить график

4. Сделать вывод

Исходные данные:

Время моделирования – 10 – 30 минут

Вероятность появления клиента – 1- 20 минут

Объем работы:

Теоретическая часть – 5-15 стр.

Практическая часть – 4-5 стр.

Теоретическая часть.

Современные производственные системы и методы их формализации.

Классификация производственных систем

Изучение современного производства, разработок и проектов показывает, что спектр решений гибких производственных систем простирается от производственных модулей на базе одного станка с ЧПУ до объединенных компьютером производственных участков и цехов.

Основными классификационными признаками ГАП являются:

масштабность структуры;

сфера использования (по группам отраслевых производств, видам работ, массе и габаритам продукции);

технический уровень (гибкость, степень автоматизации, рост производительности).

По масштабности ГАП разделяется:

Гибкий производственный модуль (ГПМ)

Единица технологического оборудования для производства изделий произвольной номенклатуры в установленных пределах значений их характеристик с программным управлением, автономно функционирующая, автоматически осуществляющая все функции, связанные с их изготовлением, имеющая возможность встраивания в гибкую производственную систему.

Гибкая производственная система (ГПС)

Совокупность в разных сочетаниях оборудования с ЧПУ, роботизированных технологических комплексов, гибких производственных модулей, отдельных единиц технологического оборудования и систем обеспечения их функционирования в автоматическом режиме в течение указанного интервала времени, обладающая свойством автоматизированной переналадки при производстве изделий произвольной номенклатуры в установленных пределах значений их характеристик.

Гибкая автоматизированная линия (ГАЛ)

Гибкая производственная система, в которой технологическое оборудование расположено в принятой последовательности технологических операций.

Гибкий автоматизированный участок (ГАУ)

Гибкая производственная система, функционирующая по технологическому маршруту, в котором предусмотрена возможность изменения последовательности использования технологического оборудования.

Гибкий автоматизированный цех (ГАЦ)

Гибкая производственная система, представляющая собой в различных сочетаниях совокупность гибких автоматизированных линий, роботизированных технологических комплексов, гибких автоматизированных участков, роботизированных технологических участков для изготовления изделий заданной номенклатуры.

Гибкий автоматизированный завод (ГАЗ)

Гибкая производственная система, представляющая собой совокупность ГАЦ.

По степеням автоматизации ГПС подразделяются на гибкие производственные комплексы (ГПК) и гибкие автоматизированные производства (ГАП).

ГПК определяется как ГПС, состоящая из нескольких ГПМ, объединенных автоматизированной системой управления и автоматизированной транспортно-складской системой, автономно функционирующая в течение заданного интервала времени и имеющая возможность встраивания в систему более высокой системы автоматизации.

ГАП представляет собой ГПС, состоящую из одного или нескольких ГПК, объединенных автоматизированной системой управления и транспортно-складской системой.

Роботизированный технологический комплекс (РТК)

Совокупность единицы технологического оборудования, промышленного робота и средств оснащения, автономно функционирующая и осуществляющая многократные циклы. РТК, предназначенные для работы в ГПС, должны иметь автоматизированную переналадку и возможность встраивания в систему. Средствами оснащения РТК могут быть: устройства накопления, ориентации, поштучной выдачи объектов производства и другие средства, обеспечивающие функционирование РТК.

Система обеспечения функционирования ГПС.

Совокупность в общем случае взаимосвязанных автоматизированных систем, обеспечивающих проектирование изделий, технологическую подготовку их производства, управление гибкой производственной системой при помощи ЭВМ и автоматическое перемещение предметов производства и технологической оснастки.

В общем случае в систему обеспечения функционирования ГПС входят:

- автоматизированная транспортно-складская система (АТСС);

- автоматизированная система инструментального обеспечения (АСИО);

- система автоматизированного контроля (САК);

- автоматизированная система удаления отходов (АСУО);

- автоматизированная система управления технологическими процессами (АСУ ТП);

- автоматизированная система научных исследований (АСНИ);

- система автоматизированного проектирования (САПР);

- автоматизированная система технологической подготовки производства (АС ТПП);

- автоматизированная система управления (АСУ) и т.д.

- Автоматизированная транспортно-складская система (АТСС).

По гибкости ГПС делятся на системы:

а) высокой гибкости у которых номенклатура продукции, приведенная на один обрабатывающий модуль, превышает 100 наименований. Затраты времени на переналадку для обработки новой детали в пределах группы не более 10% полезного фонда времени работы.

б) средней гибкости - номенклатура продукции, приведенная на один модуль, 20 - 100 наименований. Затраты времени на переналадку - 20 %.

в) малой гибкости - номенклатура - до 20 наименований; затраты времени на переналадку более 20 %.

По степени автоматизации ГПС делятся на системы:

а) высокой (высшей) степени - автоматическое управление и трехсменный режим работы;

б) средней степени - непрерывное автоматизированное управление при многостаночном обслуживании с коэффициентом многостаночности более 2.

в) малой степени - коэффициент многостаночности не более 2.

Основные характеристики гибкого автоматизированного производства

Важнейшие характеристики ГАП:

производительность;

гибкость;

31

эффективность;

Определяются, во-первых, характеристиками осн

31

овного (станки) и вспомогательного (накопители, системы автоматизированного контроля и измерений и т.д.) оборудования и во-вторых, удачностью компоновки оборудования в ГПС.

Производительность ГПС

Это важнейший показатель эффективности производственного процесса. Наиболее надежным и удобным количественным критерием производительности являлась производительность, измеряемая количеством изделий, произведенных в единицу времени (шт/ч), или ее обратная величина - трудоемкость изготовления конкретного изделия.

Привязка этих показателей к конкретному изделию делает их малоэффективными для оценки производительности процесса, с выхода которого снимаются разные изделия. ГПС производит не только разные детали, но и разное их число в единицу времени.

Производительность нельзя рассматривать без таких понятий как гибкость и мобильность.

Понятие о гибкости автоматизированного производства

Гибкость:

o возможность обрабатывать на одной и той же технологической линии различные детали в различных сочетаниях;

o возможность изменения в любой момент стратегии производства в зависимости от необходимости;

o модифицирование обрабатываемых деталей без привлечения дополнительных значительных затрат;

o изменение состава технологической линии в зависимости от требований;

o повторное использование значительного процента существующих капиталовложений в том случае, если приходится полностью менять тип продукции.

Гибкость и производительность - это такие два фактора, которые очень трудно объединять, и поэтому только из анализа этих факторов можно определить их оптимальное соотношение для объединения, и этот анализ должен выполняться совместно конструктором и потребителем.

Этот анализ должен способствовать определению того, как и насколько гибкая система производства может влиять и сокращать себестоимость продукции, где под себестоимостью продукции понимается как прямая стоимость производства, так и все косвенные затраты производства, которые могут быть изменены благодаря применению этой новой современной системы производства.

Гибкие производственные системы обычно состоят из определенного количества станков, системы транспортировки и разгрузки деталей и системы управления, состоящей из одной или нескольких ЭВМ и соответствующего математического обеспечения.

Станки могут быть специализированные или универсальные, одинаковые или различные, более или менее гибкие, оснащенные или нет какой-либо особенной аппаратурой.

Система транспортировки может быть организована для транспортировки деталей, оснастки, палет (спутников) или же только для перевозки деталей; может быть более жесткой (например, линия на роликах с приводом), или же более гибкой (например, самоходные тележки на рельсах или с управлением по проводу; может выполнять только подачу отдельных деталей, а затем роботы будут забирать эти детали и закреплять или снимать их на оснастке станков.

Может, наконец, выполнять перевозку только деталей, либо также и перевозку инструментов.

Система управления может быть простейшей (управление только одним движением тележек или деталей) или может усложняться и быть системой, которая управляет программой обработки деталей, магазином с инструментами, качеством обработки, стратегией, - которые изменяются в зависимости от требований производства; наконец, может быть сложнейшей системой комплексного управления цехом со всеми его составными частями.

Практическая часть

Задание 1.

На предприятии существует 5 видов производства в соответствии с которым выпускается 700, 150, 400, 80, 170 тыс. ед. продукции. При этом используется 30, 50, 75, 40, 80 тонн стали соответственно. Величина запаса составляет 17% от используемого. Прибыль от реализации продукции составит 3; 1,1; 1,2; 0,6; 1,1 млн. руб. соответственно. Составить уравнение математической модели.

Количество конечной продукции, т.е. прибыль от реализации продукции, производимой в течение единицы времени, обозначим через Cј. Обозначим число ј-х технологических способов производства через n (ј=1,n). Обозначим число исходных i-х ресурсов, необходимых для производства конечной продукции через m (i = um). Пусть bi - величина запаса i-гo исходного ресурса, которым располагает предприятие. Обозначим через aij расход i-ro исходного ресурса за единицу времени использования j-гo технологического способа производства.

В качестве параметров управления в данной задаче примем время функционирования каждого из технологических способов производства. Положим Xj равным времени, в течение которого предприятие выпускает продукцию.

Составление уравнения математической модели эквивалентно выбору (нахождению) конкретных значений для каждого из неизвестных пока параметров управления Xj . Целевой функцией в рассматриваемой задаче является выражение количества конечной продукции через параметры управления Xj , т.е. тот план производства считается лучше, при котором выпуск конечной продукции больше. Если Cj*Xj - это объем конечного продукта, произведенного j-м технологическим способом, то общий объем конечного продукта, выпущенного предприятием, который должен быть максимизирован, представляем в виде следующего выражения.

где Cij - объем выпуска продукции i-гo вида;

f(x) = 700Х1+150Х2+400Х3+80Х4+170Х5 мах

Т.к. выпуск продукции должен максимизировать прибыль, то составим

следующее выражение:

f(x) = 3Х1+1,1Х2+1,2Х3+0,6Х4+1,1Х5 мах

При этом ограничен расход материала, запас которого составляет 17 тонн

стали.

= СаХа≤bi, i=1,m,

30Х1+50Х2+75Х3+40Х4+80Х5≤0,17(30+50+75+40+80)

30Х1+50Х2+75Х3+40Х4+80Х5≤46,75, i=1,75 (2)

где Са - расход материала на производство единицы изделия i-oгo вида (определяется как отношение затрат материала на выпуск продукции i-oгo вида к выпуску продукции);

bj - величина запаса ресурса, которым располагает предприятие.

Поскольку запас i-го ресурса, которым располагает предприятие, равен bj, то полный расход этого ресурса не превосходит величину его запасов.

Учитывая физическую сущность параметров управления (время исполнения технологических способов не может быть отрицательным), математическая постановка задачи должна быть дополнена условиями, не допускающими отрицательные значения параметров управления Xj

Xj≥0, j=1,n. (3)

Система неравенств (2) и (3), состоящая из m + n неравенств, является полной системой ограничений задачи и определяет множество допустимых планов.

Математическая модель рассматриваемой задачи планирования работы предприятия определяется соотношениями (1), (2), (3) и состоит в максимизации целевой функции (1) при соблюдении ограничений (2) и (3).

Задание 2.

Рассмотрев предложенную организационную структуру проанализируйте ее эффективность с использованием методов моделирования производственных систем.

9

11

13

10

1

3

2

8

4

7

15

6

5

12

17

16

14

Для проведения структурного анализа организационной структуры предприятия представим ее в виде графа G = {X, U}, где X - множество вершин (|Х| = n), соответствующее множеству структурных элементов; U -множество ребер (|U| = m), соответствующее множеству связей между структурными элементами предприятия.

Для описания графа G построим матрицу смежности (таблица 1), которая для неориентированного графа имеет вид А= ||аij||, где аij - элементы матрицы смежности, определяемые следующим образом:

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

Pi

Pi²

ri

1

1

1

1

0.03

2

1

1

1

3

9

0.09

3

1

1

1

3

9

0.09

4

1

1

1

1

4

16

0.12

5

1

1

1

3

9

0.09

6

1

1

2

4

0.06

7

1

1

1

3

9

0.09

8

1

1

1

3

9

0.09

9

1

1

1

0.03

10

1

1

1

3

9

0.09

11

1

1

1

0.03

12

1

1

1

0.03

13

1

1

1

0.03

14

1

1

1

0.03

15

1

1

1

0.03

16

1

1

1

0.03

17

1

1

1

0.03

1. По матрице смежности определим ранг каждого элемента

для нашего случая ΣΣaij = 33, Ранги структурных элементов приведены в последнем столбце таблицы 1.

Чем выше ранг элемента, тем более сильно он связан с другими
элементами и тем более тяжелыми будут последствия при потере качества
его функционирования, В нашем случае наиболее высокий ранг (0.12) имеет
четвертый элемент структуры.

2. Проверим связность структуры.

Для связных структур (не имеющих обрывов и висячих элементов) должно выполняться условие

Правая часть неравенства определяет необходимое минимальное число
связей в структуре графа, содержащего n вершин.

Для нашего случая n(количество структурных элементов) равно 17 и
условие 1/2 33 = 17-1 выполняется, т. е. структура является связной.

3. Проведем оценку структурной избыточности R, отражающей
   превышение общего числа связей над минимально необходимым:

где m - множество ребер графа (1/2 количества связей в матрице смежности);

n - количество вершин (элементов) структуры;

где aij - элементы матрицы смежности.

Данная характеристика является косвенной оценкой экономичности и надежности исследуемой структуры и определяет принципиальную возможность функционирования и сохранения связей системы при отказе некоторых ее элементов. Система с большей избыточностью R потенциально более надежна, но менее экономична. Возможны три варианта: если R< 0, то система несвязная; R = 0, система обладает минимальной избыточностью; R > 0, система имеет избыточность; чем выше R, тем выше избыточность.

Для нашего случая R = 33*0.5/(17-1)-1= 0,031, т. е. структура имеет избыточность.

4. Определим неравномерность распределения связей - Е. данный показатель характеризует недоиспользование возможностей данной структуры, имеющей m ребер и n вершин, в достижении максимальной связности. Величина Е определяется по формуле

где - вес i-гo элемента, или количество связей i-го элемента со

всеми остальными.

Для нашего случая Е= 3,87.

Однако для сравнения различных структур по неравномерности связей используют относительную величину:

где Е_мах - максимальное значение неравномерности связей, которое достигается в системе, имеющей максимально возможное число вершин, имеющих одну связь.

Величину Е определяют но эмпирической формуле

Для нашего случая у- 16.5-17=-0,5; х= 0.615

Тогда Е_mах=14.35

Определим величину Е для нашего случая. Е = 3.84/14.35 = 0.27 Величина E для различных типов структур изменяется от 0 (для структур с равномерным распределением связей) до 1,

В нашем случае распределение связей в структуре довольно равномерное.

5. Определим структурную компактность структуры Q, которая отражает общую структурную близость элементов между собой. Для этого используем формулу

где dij - расстояние от элемента i до элемента j, т. е. минимальное число связей, соединяющих элементы i и j.

Для определения величины общей структурной компактности построим матрицу расстояний D = || dij || - (таблица 2), По таблице определяем Q = 336,

Таблица 2 - Матрица расстояний D

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

сумма

1

1

2

2

3

3

3

3

4

4

4

4

4

4

4

5

5

55

2

1

1

1

2

2

2

2

3

3

3

3

3

3

3

4

4

40

3

2

1

2

1

1

3

3

2

2

2

4

4

4

4

3

3

41

4

2

1

2

3

3

1

1

4

4

4

2

2

2

2

5

5

43

5

3

2

1

3

2

4

4

1

1

3

5

5

5

5

2

2

48

6

3

2

1

3

2

4

4

3

3

1

5

5

5

5

4

4

54

7

3

2

3

1

4

4

2

5

5

5

1

1

3

3

6

6

54

8

3

2

3

1

4

4

2

5

5

5

3

3

1

1

6

6

54

9

4

3

2

4

1

3

5

5

2

4

6

6

6

6

3

3

63

10

4

3

2

4

1

3

5

5

2

4

6

6

6

6

1

1

59

11

4

3

2

4

3

1

5

5

4

4

6

6

6

6

7

7

73

12

4

3

4

2

5

5

1

3

6

6

6

2

4

4

7

7

69

13

4

3

4

2

5

5

1

3

6

6

6

2

4

4

7

7

69

14

4

3

4

2

5

5

3

1

6

6

6

4

4

2

7

7

69

15

4

3

4

2

5

5

3

1

6

6

6

4

4

2

7

7

69

16

5

4

3

5

2

4

6

6

3

1

5

7

7

7

7

2

74

17

5

4

3

5

2

4

6

6

3

1

5

7

7

7

7

2

74

Однако для количественной оценки структурной компактности и возможности объективного сравнения различных организационных структур чаще используют относительный показатель определяемый по формуле:

где Q_min = n (п-1) - минимальное значение компактности для структуры типа «полный граф» (каждый элемент соединен с каждым).

Для нашей структуры Q_min =17*(17-1)=272. Тогда ⁼ 1008/272—1 = 2,7

Структурную компактность можно характеризовать и другой характеристикой - диаметром структуры: d = max dij, равным максимальному значению расстояния dij в матрице расстояний. Для нашей структуры d = 7.

С увеличением Q_0TH и d увеличиваются средние временные задержки при обмене информацией между подразделениями, что вызывает снижение общей надежности. С этой точки зрения, структура исследуемого предприятия имеет надежность низкого уровня (максимальную надежность имеет полный граф, для которого Qотн=0, a d =1).

Для характеристики степени централизации системы используется показатель центральности структурного элемента;

который характеризует степень удаленности i-го элемента от других элементов структуры.

Чем меньше удален i-й элемент от других, тем больше его центральность и тем большее количество связей осуществляется через него. В нашем случае наиболее центральным является первый элемент, для которого Σdij=40-min, то есть он обладает максимальным коэффициентом центральности Z_{max =}272/2*40=4.

Степень центральности в структуре в целом может быть охарактеризована индексом центральности:

Таким образом δ=3.

Значение степени центральности находится в диапазоне 1 ≥ 5 ≥ 0, при этом для структур с равномерным распределением связей δ = 0, для структур, имеющих максимальную степень централизации, δ = 1.

Для нашего случая среднее значение степени центральности структуры предъявляет достаточные требования к пропускной способности центра (элемент 2), через который устанавливается большое число связей по приему и переработке информации, и надежности его функционирования, так как отказ центрального элемента ведет к полному разрушению структуры.

Задание 3.

Мы имеем производственное подразделение, которое обслуживает клиентов. В нашем случае обслуживается один клиент, время появления которого от 1 до 20 минут. Для построения математической модели обслуживания определим вероятность появления клиента в установленный отрезок времени. По теории вероятности вероятность появления клиента за одну минуту равна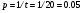, а вероятность его отсутствия q=l-p=l-0.05=0.95.

0 + 0,05 - 1

+ клиент пришел

- клиент не пришел

Для построения математической модели производство используем один из основных законов непрерывного распределения вероятностей - это показательное распределение.

По этому закону плотность распределения вероятности появления клиент выражается формулой

f (х) = λ-e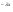 , х > 0

А функция распределения случайной величины X в нашем случае это вероятность появления одного клиента имеет вид

F(x)=l – e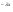 λ >0,0≤х<∞

λ — параметр показательного распределения.

Математическое ожидание появления одного клиента, обратно его параметру.

m_х = , m_х = n * р = 20 * 0.05 = 1,

отсюда λ = 1 и формулы имеют вид:

f (х) = e

F(x)=l - e

Таблица расчетов

f (х)

1

0,37

0,14

0,05

0,02

0,007

0,003

0,001

…

→0

х

0

1

2

3

4

5

6

7

…

20

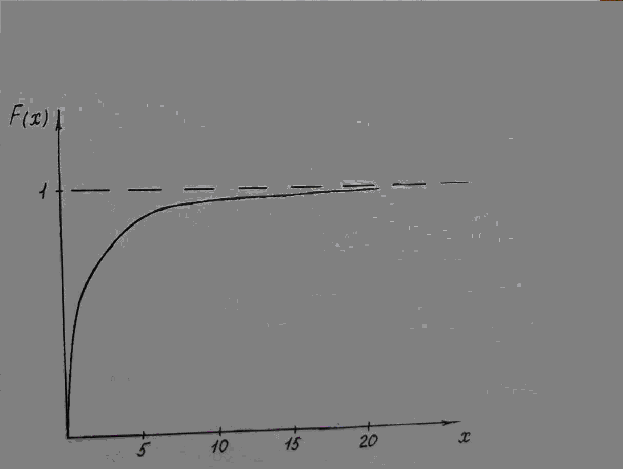
Используя данные расчетов, построим график функции F(x) показательного распределения вероятности появления одного клиента 0≤ F(x)<1

F(x)

0

0,63

0,86

0,95

0,98

0,993

0,997

0,99

→1

х

0

1

2

3

4

5

6

7

…

20

Вывод: Методы моделирования предприятия на основе теории вероятности являются наиболее доступными, но в значительной мере приближенными.

В зависимости от применяемого метода определяется плотность моделирования и точность получаемого результата.

Список используемой литературы.

1. Иозайтис В. С., Львов Ю.А. Экономико-математическое моделирование производственных систем: Учеб. пособие для инж.-экон. спец. вузов. М.: Высш. шк., 1991.

2. Советов Б.Я., Яковлев С.А. Моделирование систем: Учеб. для вузов. М.: Высш. шк., 1998.

3. Имитационное моделирование в оперативном управлении производством / Н.А. Саломатин, Г.В. Беляев, В.Ф. Петроченко, Е.В. Прошлякова. М.: Машиностроение, 1984.

4. Скурихин В.И. и др. Математическое моделирование.– Киев: 1983.

5. Лычагин М. В., Мироносецкий Н.Б. Моделирование финансовой деятельности предприятия/ Отв. ред. Макаров В.Л.– Новосибирск: Наука, 1986.

6. Анализ и моделирование производственных систем / Б. Г. Тамм, М. Э. Пуусепп, Р. Р. Таваст ; Под общ. ред. Б. Г. Тамма. М. Финансы и статистика 1987.