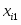Однофакторный дисперсионный анализ

В общем виде эту задачу можно поставить следующим образом: пусть мы наблюдаем m независимых нормально распределенных случайных величин 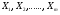(1) предполагая, что все они имеют одинаковую дисперсию 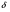(эту гипотезу можно проверить с помощью F-критерия). Средние значения случайных величин 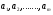(2) вообще говоря, различны. Пусть в одинаковых экспериментальных условиях над каждой из переменных (1) производится некоторая серия наблюдений (для простоты ограничимся случаем равночисленных наблюдений, хотя это обстоятельство несущественно для теории). Данные k-й серии пусть будут 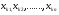(k=1,2,…..,m) (3).

Опираясь на эти статистические данные, мы хотим проверить гипотезу, согласно которой средние значения (2) равны, т.е. a₁=a₂=…..=a_m(4)

Если проверяемая гипотеза, называемая нулевой гипотезой, верна. поставив средние в каждой серии, мы не должны получить ш расхождения между ними; если такое расхождение обнаружено то гипотезу (3) приходится отбросить.

Примером подобной ситуации может служить статистическое исследование урожайности сельскохозяйственной культуры в зависимости от 1 из m сортов почвы при некотором способе ее обработки. Истинное значение урожайности для каждого из m сортов почвы неизвестно, а экспериментально наблюдаемые урожайности (3) в каждом из n экспериментов на этих сортах почвы содержат ошибки, возникающие из-за тех или иных случайных причин. Будет ли одинаковой урожайность на всех сортах почвы, если предположить, что измерения (3) проводились с ‚одинаковой точностью и в одинаковых условиях? Иначе говоря, мы хотим проверить влияние одного фактора сорта почвы — на урожайность .сельскохозяйственной культуры. В другой постановке та же задача возникает, если мы хотим проверить, насколько влияют и влияют ли вообще на плодородие почвы источники загрязнения. В этом случае сорт почвы может меняться и давать разную урожайность в зависимости от удаленности обрабатываемого участка земли от источника загрязнения.

Таблица результатов измерений будет иметь следующий вид (табл. 1):

Результаты измерений урожайности

Номер сорта почвы

Номер эксперимента

1

2

3

…

n

1

x₁₁

X₁₂

X₁₃

…

X_1n

2

X₂₁

X₂₂

X₂₃

…

X_2n

3

X₃₁

X₃₂

X₃₃

…

X_3n

…

…

…

…

…

…

m

X_m1

X_m2

X_m3

…

x_nm

Обозначим через 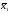среднее арифметическое из n наблюдаемых урожайностей на почве первого сорта, через 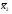— среднее из урожайностей в почве второго сорта и т. д., так, что

, …,

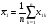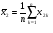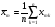
Систематические ошибки наблюдений урожайностей на разных почвах неодинаковы, то мы должны ожидать повышенного рассеивания выборочных средних.

Обозначим через 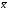общее среднее арифметическое всех n m измерений так, что 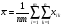.(5)

Суммирование по k при постоянном i дает сумму по всем наблюдениям i-той серии (т.е. по i-му сорту почвы). Дальнейшее суммирование по i дает итог по всем сортам почвы. Так как

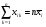, то .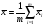

В то же время

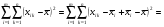
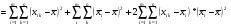,(6)

причем

.

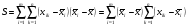Но 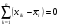, так как представляет собой сумму отклонений наблюдений i-й серии от средней этой же серии и потому S=0. (7)

По этому приняв во внимание, что

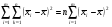,(8)

мы можем основное тождество (6) записать в следующем виде

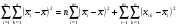, (9) или в сокращенном виде 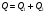,(10)

где , ,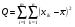

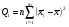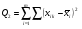
Таким образом, общая сумма квадратов ‚ распадается на две составные части, первая из которых связана с оценкой дисперсии урожайности между сортами почвы, а вторая — с оценкой дисперсии внутри всех сор почвы.

Предположим теперь, что гипотеза (4) верна, и потому нормальные распределения всех величин 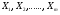(урожайностей) тождественны. имеют одинаковые среднее значение и дисперсию 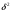.Тогда же nm наблюдений можно рассматривать как выборку из одной и той же нормальной совокупности .

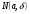Можно показать, что при этой гипотезе статистик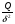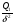и , и 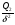распределены по закону 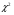соответственно с 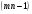,,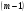 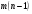степенями свободы, а по тому Q, Q₁, Q₂ могут быть использованы в этом случае для оценки 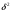. Эта оценка может быть поведена с помощью несокращенных характеристик

, , .

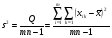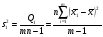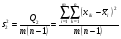При более детальном изучение показывает, что Q₁ и Q₂ при нашей гипотезе независимы друг от друга. Заметим, этот вывод справедлив при любых предположениях относительно a_i.

Из сказанного вытекает, что критерий

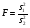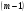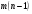(11) в гипотезе (4) будет следовать F-распределению с и степенями свободы. Выбирая q%-й уровень значимости при известных 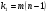, , 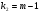найдем по таблице 20 в приложение соответствующий q% предел 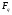так, что P(F>F_q).

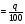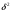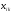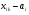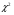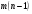Пусть с другой стороны наша гипотеза неверна и средние значения (2) не равны друг другу, но параметр во всехm совокупностях один и тот же, когда сумма Q₂, не изменяющаяся при замене на , имеет, как можно доказать. По-прежнему распределение и степенями свободы, .

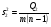По-прежнему является несмещенной оценкой для 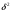. В то же время числитель F в (7,14) учитывает систематические расхождения между средними значениями a_i, и имеет тенденцию расти и становится тем больше, чем больше отклонения от предполагаемого равенства значений a_i. Поэтому правила проверки гипотезы дается в следующем виде: a₁=a₂=…..=a_m принимается, если 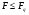; в этом случае 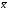и 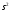несмещенными оценками параметров a и 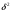нормально распределенных случайных величин (1).

Если 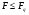,то нулевая гипотеза отклоняется, и следует считать, что среди значений 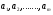имеются хотя бы два не равных друг другу.

Схема однофакторного дисперсионного анализа

Компонента дисперсии

Сумма квадратов

Число степеней свободы

Выборочная дисперсия

Между сортами почвы

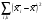
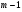
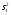
Внутри сортов почвы

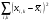
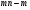
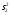
Полная (общая)

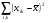
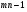
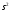
Сравнивая дисперсию между сортами почвы с дисперсией «внутри» почвы, по величине их отношения (11) судят, насколько рельефно проявляется влияние такого фактора, как сорт почвы; в этом сравнении как раз и заключается основная идея дисперсионного анализа. Схему однофакторного дисперсионного анализа можно представить в , табл. 2.

В качестве числового примера рассмотрим данные пятикратного (n=5) измерения урожайности на трех (т =3) сортах почвы. В таблице приведены данные не фактического, а условного эксперимента;

Результаты измерения урожайности в относительных единицах

Номер

Сорта почвы

Номер эксперимента

Выборочное среднее

1

2

3

4

N=5

i

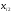
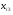
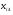
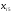
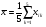
1

12

15

17

13

16

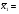14.6

2

20

17

16

25

14

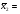18.4

m=3

10

12

11

13

8

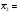10.8

Из таблицы имеем:

;

;

; ; ; .

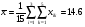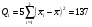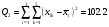
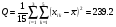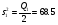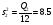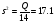Для нашего примера таблица однофакторного анализа будет иметь следующий вид

дисперсионный анализ урожайности на различных сортах почвы

Компонента дисперсии

Сумма квадратов

Число степеней свободы

Выборочная дисперсия

Между сортами

почвы

Q₁=137

2

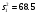
Внутри сортов почвы

Q2=102.2

12

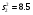
Полная (общая)

Q₃=239.2

14

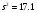
Произведя теперь проверку нулевой гипотезы (4) с помощью 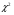распределения, находим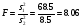

При двух степенях свободы большей дисперсии (k₁ = 2) и 12 е свободы меньшей дисперсии (k₂ = 12) по табл. в приложении II находим критические границы для F, равные при 5%-м уровне pзначимости и 3.88 и 1%-м уровне — 6.93. Полученное нами из наблюдений значение 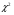превышает указанные границы, и потому нулевая гипотеза должна быть отвергнута, т.е. урожайность на рассматриваемых сортах почвы неодинакова.