Проектирование комбинационных схем










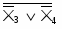
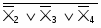

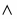
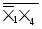
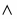
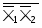
 СОДЕРЖАНИЕ
СОДЕРЖАНИЕ
Введение
1.Комбинационные схемы. Основные понятия
2.Проектирование комбинационных схем в булевом и монофункциональном базисах
3.Проектирование комбинационных схем с учетом коэффициентов объединения по входу и выходу
Вывод
Литература
Введение
Тема реферата «Проектирование комбинационных схем».
Цель написания работы – ознакомление с основными понятиями комбинационных схем; обучение проектированию комбинационных схем в булевом и монофункциональном базисах, а также с учетом коэффициентов объединения по входу и выходу.
1.Комбинационные схемы. Основные понятия
Комбинационной схемой (КС) называется схема из логических (переключательных) элементов, реализующая булеву функцию или совокупность булевых функций. В общем случае КС можно представить схемой, приведенной на рис. 1, где х1, х2,....хn — входы КС, f1, f2,...,fm — ее выходы.
ÊÑ õ1 õ2 ... õn f1 f2 ... fm
Рисунок. 1
Под логическим (переключательным) элементом чаще всего понимают техническое устройство, реализующее одну элементарную булеву функцию.
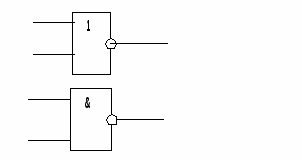
Прикладная теория цифровых автоматов не рассматривает физические явления, лежащие в основе разработки и функционирования логических элементов. Обычно логический элемент понимается как «черный ящик» и учитывается только реализуемая элементом булева функция. Примеры логических элементов ИЛИ — НЕ, И — НЕ, реализующих соответствующие булевые функции двух переменных, представлены на рис. 2.
Рисунок 2
Под глубиной (числом уровней) КС понимается максимальное число логических элементов, расположенных на пути следования сигнала от входов КС к ее выходу. Глубина КС оказывает существенное влияние на быстродействие КС, так как каждый логический элемент обладает внутренней задержкой распространения сигнала. Одно- и двухуровневые КС обладают максимальным быстродействием. Однако они не всегда могут быть использованы, поскольку число входов реальных логических элементов в интегральном исполнении ограничено.
Если КС реализует одну булеву функцию, то она называется одновыходовой КС (рис. 3). Если КС реализует совокупность булевых функций, то она называется многовыходовой КС.
Рисунок 3
Комбинационным схемам соответствуют схемы без обратных связей (под обратной связью понимается соединение выхода некоторого логического элемента со своим входом, возможно, через цепочку других логических элементов (рис. 4)).
Рисунок 4
Логические элементы, используемые для построения КС, характери-зуются определенными техническими парамет-рами, среди которых наиболее важные коэффи-циент объединения по входу І; коэффициент объединения по выходу U (коэффи- циент разветвления) и задержка сигнала ∆ τ в логическом элементе.
Система функций, реализуемая выбранной для синтеза схем совокупностью логических элементов, всегда должна быть функционально полной, т. е. допускать реализацию любой булевой функции на основе принципа суперпозиции. Если в качестве системы функций выбраны функции И, ИЛИ, НЕ, то считают, что реализован булев базис. Проектирование КС в булевом базисе наиболее просто, так как методы минимизации булевых функций в основном ориентированы на него. Поэтому, как правило, на первом этапе КС проектируется в булевом базисе с последующим переходом в заданный базис. Если выбраны функции И-НЕ или ИЛИ-НЕ, то считают, что реализуется универсальный или монофункциональный базис. Для удобства проектирования в различных системах элементов возможна реализация и смешанного базиса.
Конструктивно логические элементы объединяются в единые корпуса — интегральные микросхемы (ИМС). В общем случае, под интегральной микросхемой понимается микроэлектронное изделие, имеющее высокую плотность упаковки элементов и соединений между ними; при этом все элементы выполнены нераздельно и электрически соединены между собой таким образом, что с точки зрения спецификации, испытаний, поставки и эксплуатации изделие рассматривается как единое.
Число логических элементов, объединяемых в один корпус ИМС, характеризует степень интеграции логических элементов. Степень интеграции влияет на надежность, габаритные размеры, энергопотребляемость проектируемых КС. Различают ИМС малой, средней, большой и сверхбольшой степени интеграции.
В настоящее время используютоценки: до 100 000 вентилей — БИС, более 100000 вентилей—СБИС.
Коэффициент объединения І по входу логического элемента ИМС задает максимальное число логических элементов, выходы которых могут быть объединены на входе данного элемента.
Коэффициент объединения U по выходу (коэффициент разветвления) логического элемента ИМС задает максимальное число входов логических элементов, которые могут быть соединены с выходом данного логического элемента без нарушения режима его работы.
Если некоторый логический элемент КС оказался перегруженным по выходу (после окончания проектирования КС), то необходимо произвести эквивалентное преобразование структуры КС с целью его разгрузки. Это преобразование сводится либо к введению в КС специальных усилителей-формирователей, либо к дублированию данного логического элемента.
Задержка ∆ τ логического элемента характеризует промежуток времени между моментами установления сигналов на входах и выходах логического элемента. Распространение сигнала по КС в зависимости от задержек логических элементов, через которые он проходит, характеризует быстродействие КС. Прохождение сигналов по различным путям в КС вызывает появление различных задержек, что может послужить причиной неустойчивого функционирования КС.
Современные средства вычислительной техники собираются из ИМС, типовых как по физическим принципам функционирования, так и по выполняемым логическим функциям.
Основные требования к комплекту ИМС следующие:
1) ИМС комплекта должны обеспечивать возможность построения различных устройств и систем обработки цифровой информации;
2) число различных типов ИМС должно быть оптимальным, чтобы обеспечивалась простота эксплуатации сложных систем и взаимозаменяемость их частей;
3) в комплекте должны быть предусмотрены ИМС, которые не выполняют логических функций, а согласуют нагрузочные характеристики логических элементов и обеспечивают формирование электрических сигналов;
4) ИМС комплекта должны быть технологичными в изготовлении и удобными для проверки их электрических параметров;
5) комплект ИМС должен быть функционально полным;
6) комплект ИМС должен содержать специальные ИМС, предназначенные для построения управляющих цепей, запоминающих устройств, цепей связи запоминающих и логических устройств, согласования электромеханических устройств (реле, переключателей, механизмов перфорации и печати) и логических устройств, связи различных устройств с устройствами ввода-вывода информации, индикации информационных состояний и генерации высокостабильных тактовых сигналов.
В процессе реализации конкретных схем решаются задачи обеспечения необходимых характеристик надежности. В общем случае эти характеристики могут быть рассчитаны, исходя из надежностных характеристик элементов и конкретной схемы (это касается не только комбинационных схем). В тех случаях, когда расчетная надежность не удовлетворяет исходным требованиям, применяются специальные методы повышения надежности. Среди них наиболее интересными, с точки зрения теории цифровых автоматов, являются методы контроля работы схем с использованием помехоустойчивых кодов.
Таким образом, на этапе структурного синтеза решается задача построения комбинационной схемы, реализующей заданную совокупность булевых функций и удовлетворяющей заданным требованиям быстродействия и надежности.
2.Проектирование комбинационных схем в булевом и монофункциональном базисах
При проектировании КС на логических элементах И, ИЛИ, НЕ и отсутствии ограничений на число входов элементов пользуются изложенными ранее методами минимизации булевых функций. При наличии ограничений наиболее простым методом является применение специальных ИМС, называемых расширителями и имеющихся в комплектах ИМС. Расширители позволяют увеличить, в случае необходимости, число входов логического элемента путем включения дополнительного (точно такого же) логического элемента на один из входов основного.
а) б)
в) г)
Рисунок 5
Рассмотрим переход от реализации булевой функции в булевом базисе, т. е. на логических элементах И, ИЛИ, НЕ к схемам в монофункциональном базисе, т. е. реализованных на логических элементах ИЛИ — НЕ либо И — НЕ. Такие логические элементы широко используются в имеющихся на практике комплектах ИМС. Заметим, что если булева функция в базисе И, ИЛИ, НЕ реализована двухуровневой КС в соответствии с рис. 5, а. б, то переход к реализации в базисе И — НЕ либо ИЛИ—НЕ может быть осуществлен заменой всех элементов КС (рис. 5 а) на логические элементы ИЛИ—НЕ, и элементов КС (рис. 5.б) на логические элементы ИЛИ—НЕ с сохранением как переменных, поданных на входы элементов, так и связей между ними. Преобразованные КС представлены на рис. 5. в., г. В приведенных на рисунках схемах полагается, что на входы КС переменные поступают как с отрицанием, так и без отрицания, т. е. элемент НЕ на входах КС не учитывается.
Однако использовать в качестве внешних входов КС переменные Хі и Хі не всегда удается. В этом случае КС, реализованная в булевом базисе, может быть представлена рис.6 а,б и является трехуровневой. Соответствующие КС, реализованные в монофункциональном базисе, также будут трехуровневыми.
Существует весьма простой способ перехода от реализации КС в базисе И — НЕ к реализации КС в базисе И — ИЛИ. Способ основан на применении правил де Моргана и позволяет с помощью несложного алгоритма сразу по реализации КС в базисе И — НЕ получить реализацию КС в базисе И — ИЛИ. Если в исходной КС отсутствуют элементы И—НЕ, выполняющие функцию инвертора, то преобразованная КС будет содержать ровно столько логических элементов И, ИЛИ, сколько их имеется в исходной КС. Если в исходной КС инверторы имеются, то в преобразованной КС число логических элементов (по сравнению с исходной КС) будет уменьшено ровно на число инверторов.
Преобразование сложных аналитических выражений из булева базиса в базис ИЛИ — НЕ либо И — НЕ может быть сделано с помощью метода, основанного на последовательном применении теорем де Моргана. Метод позволяет осуществлять переход от произвольной по форме булевой функции, реализованной на элементах И, ИЛИ, НЕ, к форме, реализуемой на элементах И-НЕ, ИЛИ-НЕ, в частности от минимальной ДНФ или КНФ к минимальным (в точности до одной буквы) кратчайшим формам в базисе И-НЕ либо ИЛИ-НЕ.
а) б)
Рисунок 6
Пример. Реализовать булеву функцию
f= vvv
в монофункциональных базисах И-НЕ, ИЛИ-НЕ.
Функция задана в булевом базисе. Применив правило де Моргана, преобразуем функцию в монофункциональный базис.
f= vvv= -
преобразование в базис И-НЕ.
f=vvv= vvv-
преобразование в базис ИЛИ-НЕ.
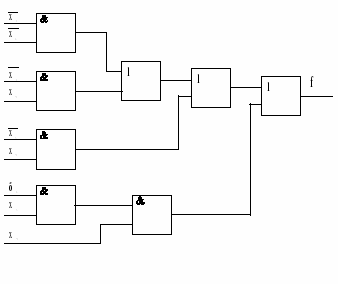
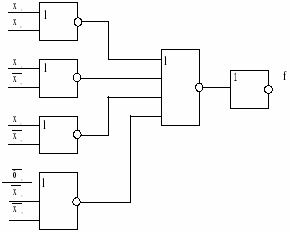
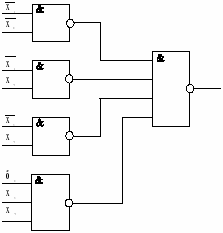
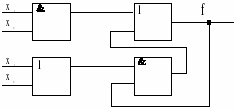
КС соответствующие данным реализациям, представлены на рис.7 а,б, соответственно.
В заключение напомним, что получение минимальных форм булевых функций в монофункциональном базисе можно представить следующим образом:
Рисунок 7. а) - реализация функции в базисе И-НЕ;
б) - реализация функции в базисе ИЛИ-НЕ.
1) получение СДНФ булевой функции;
2) получение минимальной ДНФ булевой функции на основе ее СДНФ с помощью любого известного метода минимизации булевых функций;
3) перевод минимальной ДНФ в монофункциональный базис применением теорем де Моргана в любой последовательности.
Последнее справедливо, в силу того, что применение теорем де Моргана не изменяет числа букв в выражении.
3.Проектирование комбинационных схем с учетом коэффициентов объединения по входу и выходу
Допустимая величина коэффициента объединения по входу (І) в реальных условиях проектирования КС оказывает существенное влияние на выбор ее структуры. Предположим, булева функция аналитически представлена выражением
f= vvv
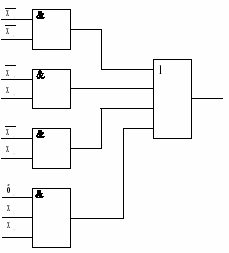
Рисунок 8
Если не учитывать коэффициент объединения по входу, то такая булева функция может быть реализована двухуровневой КС (рис. 8), являющейся оптимальным вариантом по быстродействию. Однако, если коэффициент объединения по входу І = 2, то предложенная реализация должна быть видоизменена. Преобразование КС в булевом базисе сводится к простому разделению переменных на элементах И и ИЛИ на основе ассоциативности операций конъюнкции и дизъюнкции. Преобразованная КС представлена на рис. 9. Как следует из рис.8, 9, выполненное преобразование приводит к необходимости использования четырехуровневой КС, что снижает быстродействие схемы. В общем случае, желательно проектировать КС минимальной глубины при выполнении требований на величину коэффициента І для используемого комплекта ИМС. Глубину КС можно уменьшить, если от минимальной ДНФ перейти к скобочной форме, вынося общие члены ДНФ за скобки.
В ряде случаев уменьшить глубину КС при сохранении величины коэффициента І можно, используя переход к смешанному базису, если в комплекте ИМС, используемом для проектирования КС, имеются соответствующие элементы.
Рисунок 9
Коэффициент объединения по входу U (коэффициент разветвления) некоторого логического элемента характеризует максимально возможное количество элементов схемы, входы которых могут быть подключены к его выходу. Коэффициент U является одной из технических характеристик комплекта ИМС и не связан с логикой работы ИМС. Если некоторый логический элемент α с коэффициентом разветвления U α, подключен ко входам n α > U α логических элементов, то считается, что элемент α перегружен. В этом случае необходимо так структурно преобразовать КС, возможно путем введения в нее некоторых дополнительных элементов, чтобы число нагрузок на элемент к было меньше U α. В корректно построенной КС для всех ее элементов α i должно выполняться условие отсутствия перегрузок n αi ≤ U αi Таким образом, расчет КС по коэффициенту разветвления сводится к определению перегруженных элементов и устранению перегрузок.
При построении КС с учетом коэффициента объединения по выходу наибольшее распространение получили два способа устранения перегрузок:
1) введение развязывающих усилителей;
2) дублирование перегруженных элементов.
Рисунок 10
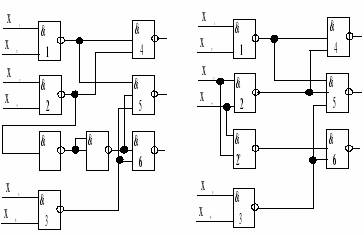
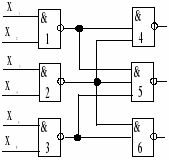
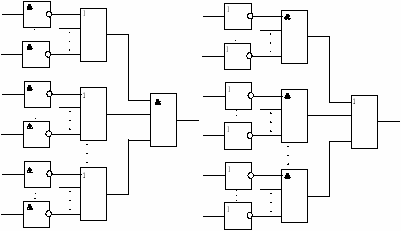
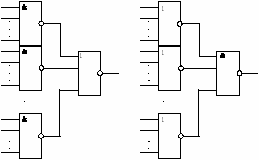
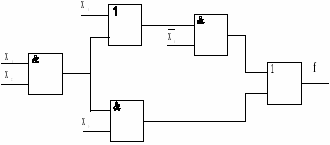
Рассмотрим их применение на конкретных примерах. Пусть задана КС (рис. 10) в монофункциональном базисе И — НЕ с коэффициентом объединения по выходу U=2. Элемент 2 в схеме перегружен, так как его выход подключен ко входам трех логических элементов КС. Установка развязывающего усилителя, состоящего из двух последовательно соединенных элементов И—НЕ (рис. 11), на выходе элемента 2 устраняет перегрузку.
Рисунок 7.11 Рисунок 7.12
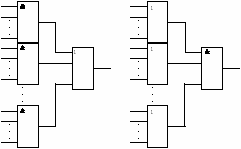
Иной способ устранения перегрузок элемента 2 сводится к его дублированию (рис. 12). Однако дублирование логического элемента повышает нагрузку на его входы, что может привести к перегрузке логических элементов, соединяемых со входами дублируемого. Ее устранение связано с введением новых дублируемых элементов и т. д. Необходимо отметить, что дублирование элементов не вносит дополнительных задержек в КС и может оказаться полезным при организации контроля правильности ее функционирования. Введение усилителей всегда вносит в КС дополнительную задержку распространения сигнала. В тех случаях, когда требуется сохранить заданное быстродействие КС и получить оптимальный вариант по числу вводимых элементов, применяют комбинированный метод, т. е. вводят усилители там, где возможно (при сохранении заданного быстродействия КС), а оставшиеся перегруженные элементы дублируют.
Вывод
В процессе написания реферата мы ознакомились с основными понятиями комбинационных схем; разобрались в проектировании комбинационных схем в булевом и монофункциональном базисах, а также с учетом коэффициентов объединения по входу и выходу.
Литература
1. Самофалов К.Г., Романкевич А.М., и др. Прикладная теория цифровых автоматов. - Киев. “Вища школа” 1987.
2. Соловьев Г.Н. Арифметические устройства ЭВМ. - М. “Энергия”. 1978.
3. Савельев А.Я. Прикладная теория цифровых автоматов - М. “Высшая школа”. 1987.
4. Каган Б.М. Электронные вычислительные машины и системы. - М. Энергоатомиздат. 1985.
5. Лысиков Б.Г. Арифметические и логические основы цифровых автоматов. - Минск. “Вышэйшая школа”. 1980.

Нравится материал? Поддержи автора!
Ещё документы из категории информатика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ