Анотація

Метою даної курсової роботи є закріплення основних теоретичних та практичних положень дисципліни комп`ютерна схемотехніка. В процесі розробки курсової роботи виконується синтез комбінаційної схеми, яка реалізує задану функцію п`яти змінних, та за результатами синтезу будується функціональна схема в заданому базисі. Потім, згідно з обраними блоками та структурою ГСА, проектуємо керуючі автомати Мура та Мілі, а також будуємо принципові схеми: для автомата Мура на елементах малого ступеня інтеграції заданої серії, а для автомата Мілі на основі ПЛМ. Ці задачі отримали широке розгалуження в аналізі та синтезі програмних і апаратних засобів обчислювальної техніки, дискретної математиці, а також мають багаточисельні технічні положення. Характерною рисою науково-технічного прогресу, який визначає подальший потужний підйом суспільно-технічного виробництва, є широке застосування досягнень обчислювальної та мікропроцесорної техніки в усіх галузях народного господарства. Вирішення задач науково-технічного прогресу потребує застосування засобів обчислювальної техніки на місцях економістів, інженерів та економічного персоналу.

1. Синтезувати комбінаційну схему, що реалізує задану функцію 5-ти змінних

1.1 Визначення значення БФ

Булева функція 5-ти змінних F (X1, X2, X3, X4, X5) задається своїми значеннями, які визначаються 7-розрядними двійковими еквівалентами чисел, що обираються з таблиці 1 за значеннями числа (А), місяця (В) народження студента і порядкового номера (С) студента в списку групи. Значення функції на конкретних наборах обираються:

– на наборах 0–6 за значенням А;

– на наборах 7–13 за значенням В;

– на наборах 14–20 за значенням С;

– на наборах 21–27 за значенням (А+В+С);

– на наборах 28–31 функція приймає невизначені значення.

Таблиця 1

О Д И Н И Ц І

0

1

2

3

4

5

6

7

8

9

0

23

11

72

12

94

38

59

10

42

25

д

1

85

95

07

49

57

50

89

13

72

39

е

2

32

23

43

94

54

76

96

37

05

96

с

3

97

87

36

08

61

48

19

18

86

62

я

4

79

72

70

02

90

63

41

47

01

20

т

5

23

26

44

92

84

33

52

51

43

38

к

6

45

74

34

35

83

87

55

93

08

07

и

7

95

80

66

60

65

88

33

05

09

48

8

27

49

19

40

17

51

47

08

37

36

9

10

59

89

99

95

77

48

11

68

20

Крім того, для всіх двійкових еквівалентів у розрядах лівіше старшої значущої одиниці, необхідно проставити символ невизначеного значення Х і вважати, що функція на таких наборах також приймає невизначені значення.

A=05. Из табл. 1 находимо число 38₁₀, яке в двоічній системі счислення має вид 0100110₂. Тут левіше старшої значущої одиницы знаходяться нулі, тому заміняємо їх символом невизначного значення Х. Тоді одержуемо Х100110.

В = 02; 72₁₀ = 1001000₂

С = 14; 57₁₀ = 0111001₂

D = А+В+С = 10100111

Запишемо значення функції F (X1, X2, X3, X4, X5) на наборах від 0 до 31 у базисі 2ЧИ-НІ

№ набора

X1

X2

X3

X4

X5

F

0

0

0

0

0

0

Х

1

0

0

0

0

1

1

2

0

0

0

1

0

0

3

0

0

0

1

1

0

4

0

0

1

0

0

1

5

0

0

1

0

1

1

6

0

0

1

1

0

0

7

0

0

1

1

1

1

8

0

1

0

0

0

0

9

0

1

0

0

1

0

10

0

1

0

1

0

1

11

0

1

0

1

1

0

10

0

1

1

0

0

0

13

0

1

1

0

1

0

14

0

1

1

1

0

Х

15

0

1

1

1

1

1

16

1

0

0

0

0

1

17

1

0

0

0

1

1

18

1

0

0

1

0

0

19

1

0

0

1

1

0

20

1

0

1

0

0

1

21

1

0

1

0

1

Х

22

1

0

1

1

0

1

23

1

0

1

1

1

0

24

1

1

0

0

0

0

25

1

1

0

0

1

1

26

1

1

0

1

0

1

27

1

1

0

1

1

1

28

1

1

1

0

0

Х

29

1

1

1

0

1

Х

30

1

1

1

1

0

Х

31

1

1

1

1

1

Х

1.2 Опис мінімізації БФ

Виписав значення функції з таблиці, одержимо мінімальну диз’юнктивну нормальну форму (МДНФ) і мінімальну кон’юнктивну нормальну форму (МКНФ) булевої функції методом карт Карно. Вибрати для реалізації мінімальну з МДНФ і МКНФ (для цього знайдемо ціну за Квайном) і представимо її відповідно до заданого елементного базису:

МДНФ:

х₁х₂х₃

х₄х₅

000

001

011

010

110

111

101

100

00

Х

1

0

0

0

Х

1

1

01

1

1

0

0

1

Х

Х

1

11

0

1

1

0

1

Х

0

0

10

0

0

Х

1

1

Х

1

0

Одержуємо мінімальну диз’юнктивну нормальну форму (МДНФ):

у =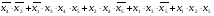

Для знайденої форми обчислимо ціну за Квайном, яка дорівнює додатку кількості слагаємих, кількості елементів та кількості заперечень.

Ц_кв. = 25

МКНФ:

х₁х₂х₃

х₄х₅

000

001

011

010

110

111

101

100

00

Х

1

0

0

0

Х

1

1

01

1

1

0

0

1

Х

Х

1

11

0

1

1

0

1

Х

0

0

10

0

0

Х

1

1

Х

1

0

Одержуємо мінімальну кон’юктивну нормальну форму (МКНФ):

у =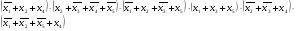

Для знайденої форми обчислимо ціну за Квайном, яка дорівнює додатку кількості помножень плюс один, кількості елементів та кількості заперечень.

Ц_кв. = 39

Виходячи з того, що ціна по Квайну МДНФ функції менше, ніж МКНФ, обираємо для реалізації МДНФ функції. Реалізацію будемо проводити згідно з заданим базисом 2ЧИ-НІ. Застосуємо до обраної форми факторний алгоритм та одержимо скобкову форму для заданої функції:

у =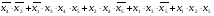

у =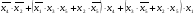

у =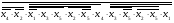

2. Вибір блоків та структури ГСА

Граф-схеми алгоритмів обираються кожним студентом індивідуально. Граф-схема складається з трьох блоків E, F, G і вершин «BEGIN» і «END». Кожен блок має два входи (A, B) і два виходи (C, D). Студенти вибирають блоки E, F, G з п'яти блоків з номерами 0, 1, 2, 3, 4 на підставі чисел А, В, С за такими правилами:

– блок Е має схему блока під номером (А) mod5;

– блок F має схему блока під номером (В) mod 5;

– блок G має схему блока під номером (С) mod 5.

Блоки E, F, G з'єднуються між собою відповідно до структурної схеми графа, що має вид

– для групи АН-042;

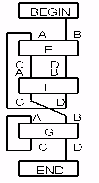
E=05 (MOD5)=0

F=02 (MOD5)=2

G=14 (MOD5)=4

Згідно з номером групи обираємо структурну схему графа, за якою з блоки E, F і G.

Тип тригера вибирається за значенням числа (А) mod 3 на підставі таблиці:

(A) mod 3

ТИП ТРИГЕРА

0

Т

D

1

D

JK

2

JK

T

автомат

Мілі

Мура

A(MOD3)= 05 (MOD3)=2; => JK триггер для автомата Мили, T-триггер для автомата Мура.

Серія інтегральних мікросхем для побудови схем електричних принципових синтезованих автоматів визначається в залежності від парності номера за списком:

– КР1533 – для парних номерів за списком;

3. Синтез автомата Мура на T-тригерах

Наш автомат має 18 станів, значить, для його побудови нам необхідно 5 T-тригерів.

Будуємо таблицю переходів автомата Мура на базі T-тригера. Виконаємо кодування станів керуючого автомата (УА) з використанням відповідного алгоритму кодування для T-триггера. Функцію порушення вихідних сигналів визначимо в залежності від поточного стану та вхідних сигналів згідно з таблицею:

Q_t

Q_t+1

T

0

0

0

0

1

1

1

0

1

1

1

0

Для кодування станів я обираю євристичний метод кодування. Я роблю це за допомогою спеціальной програми під назваю ECODE V3.02.

Таблиця для входів та виходів атомата Мура

a_m

Ka_m

a_s

Ka_s

Условие

перехода

Функция

возбуждения

а1 (–)

01100

а2

01110

1

T4

a2 (y1, y4)

01110

а5

а7

00110

01010

x3

x3

T2

T3

a3 (y1, y1)

00000

а4

а6

а8

а9

01000

00100

00010

00001

x4

x4 x2

x4 x2 x1

x4 x2 x1

T2

T3

T4

T5

a4 (y3)

01000

а7

01010

1

T4

a5 (y7)

00110

а8

а9

00010

00001

x1

x1

T3

T3 T4 T5

a6 (y4, y5)

00100

а8

00010

1

T3 T4

a7 (y2, y6)

01010

а8

00010

1

T2

a8 (y1, y8)

00010

а10

а13

а12

10010

00011

00101

x4

x4 x3

x4 x3

T1

T5

T3 T4 T5

a9 (y5, y9)

00001

а13

а13

а12

а3

00011

00011

00101

00000

x4 x3

x4 x1

x4 x3

x4 x1

T4

T4

T3

T5

a10 (y4)

10010

а11

10011

1

T5

a11 (y4, y5)

10011

а15

00111

1

T1 T3

a12 (y3, y10)

00101

а15

00111

1

T4

a13 (y6)

00011

а3

00000

1

T4 T5

a14 (y1, y3)

11111

а14

а16

11111

10111

x2

x2

–

T2

a15 (y2)

00111

а17

а16

01111

10111

x5

x5

T2

T1

a16 (y6)

10111

а17

01111

1

T1 T2

a17 (y7, y10)

01111

а14

а18

11111

01101

x4

x4

T1

T4

a18 (y2)

01101

а1

01100

1

T5

Для отримання вихідних сигналів:

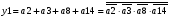
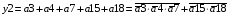
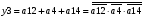
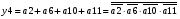
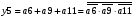
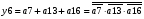
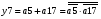
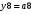
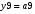
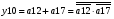
Виписуємо функцію збудження:

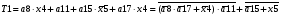
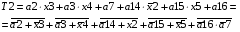
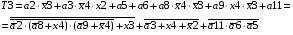
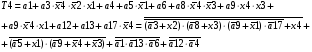
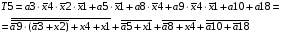
Знаходимо загальні частини та замінюємо їх на Q:

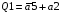
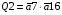
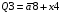
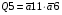
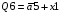
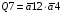
Переписуємо рівняння згідно з підстановкою:

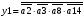
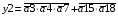
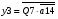
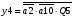
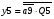
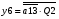
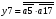
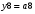
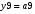
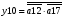
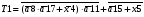
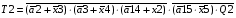
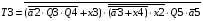
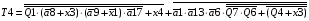
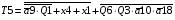
Побудова принципової схеми автомата на елементах малого ступеня інтеграції заданої серії

За допомогою отриманих виразів для вихідних сигналів і функцій порушень до типу логічних елементів, що реалізують ці вирази, та врахував проведену мінімізацію, будуємо принципову схему синтезованого автомата.

4. Синтез автомата Мілі на JK-тригерах

Наш автомат має 15 станів, значить, для його побудови нам необхідно 4 JK-тригерa.

Будуємо таблицю переходів автомата Мілі на базі JK-тригера. Виконаємо кодування станів керуючого автомата (УА) з використанням відповідного алгоритму кодування для JK-триггера. Функцію порушення вихідних сигналів визначимо в залежності від поточного стану та вхідних сигналів згідно з таблицею:

Таблиця

Q_t

Q_t+1

J

K

0

0

0

X

0

1

1

X

1

0

X

1

1

1

X

0

a1

1110

a2

0110

a3

0111

a4

0100

a5

0000

a6

1001

a7

1000

a8

1100

a9

1111

a10

1011

a11

1101

a12

0011

a13

0010

a14

0101

a15

0001

Таблиця для входів та виходів атомата Мілі

a_m

Ka_m

A_S

Ka_S

X

Y

Функція збудження

a1

1110

a2

0110

1

y1, y4

J4

a2

0110

a3

a4

0111

0100

x3

x3

y7

y2, y6

J3K4

J3

a3

0111

a12

a5

0011

0000

x1

x1

y5, y9

y1, y8

J1J4

J2K3

a4

0100

a5

0000

1

y1, y8

J2K3K4

a5

0000

a6

a7

a13

1001

1000

0010

x4

x4x3

x4x3

y4

y3, y10

y6

J4

J3

J1

a6

1001

a7

1000

1

y5, y4

J3K4

a7

1000

a8

1100

1

y2

J4

a8

1100

a9

a11

1111

1101

x5

x5

y7, y10

y6

J1K2K3K4

J1K2K4

a9

1111

a1

a10

1110

1011

x4

x4

y2

y1, y3

K1

J4

a10

1011

a11

a10

1101

1011

x2

x2

y6

y1, y3

J3K4

–

a11

1101

a9

1111

1

y7, y10

K3

a12

0011

a15

a7

a13

a13

0001

1100

0010

0010

x4x1

x4x3

x4x1

x4x3

y1, y2

y3, y10

y6

y6

J2K4

K1J2K4

J2K3K4

J2K3K4

a13

0010

a15

0001

1

y1, y2

J3

a14

0101

a4

0100

1

y2, y6

K1K2J3

a15

0001

a14

a4

a12

a5

0101

0100

0011

0000

x4

x4x2

x4x2x1

x4x2x1

y3

y4, y5

y5, y9

y1, y8

K2J4

K1K2J4

K2J4

K1K3

Для отримання вихідних сигналів:

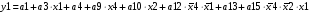
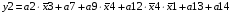
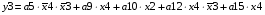
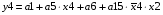
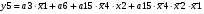
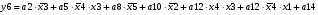
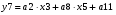
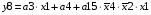
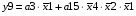
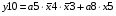
Виписуємо функцію збудження:

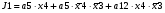
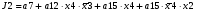
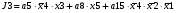
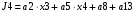
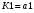
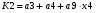
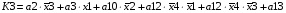
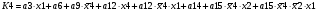
Записуємо вихідні сигнали та функцію збудження у такому виразі:

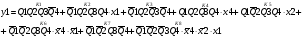
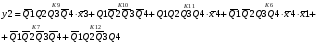
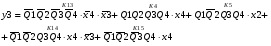
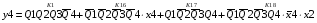
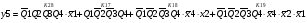
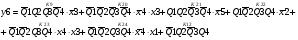
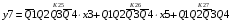
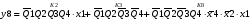
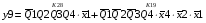
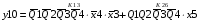
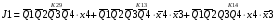
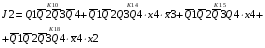
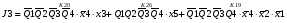
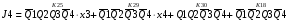
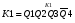
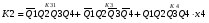
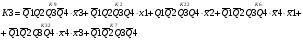
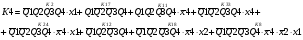
Побудова принципової схеми автомата на основі програмованих логічних матриць ПЛМ

Враховуючи отримані вирази для вихідних сигналів і функцій порушення, які підходять для побудови схеми на основі ПЛМ, наведемо таблицю з’єднань для ПЛМ, побудуємо принципову схему синтезованого автомата. При побудові принципової схеми автомата Мілі необхідно використати елементи більш високого ступеня інтеграції.

Висновки

В ході виконання даного курсового проекту був проведений аналіз основних розділів та закріплення теоретичних положень дисципліни комп`ютерна схемотехніка з метою закріплення лекційного та практичного матеріалу; також були одержані практичні навички в проектуванні принципових схем цифрових пристроїв обчислювальної техніки. У курсовій роботі були виявлені основні навички вирішення задач синтезу комбінаційної схеми та побудови функціональної схеми в заданому базисі за результатами синтезу. Також було проведене проектування керуючих автоматів Мура та Мілі за заданою граф-схемою алгоритму, а також побудування принципової схеми автоматів: для Мура – на елементах малого ступеня інтеграції заданої серії, а для Мілі – автомата на основі програмованих логічних матриць (ПЛМ). Знання, одержані під час виконання цієї роботи, використовуються для аналізу та синтезу різноманітних цифрових пристроїв обчислювальної техніки та автоматики.