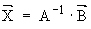
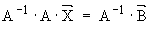
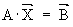
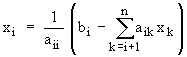
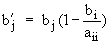
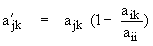
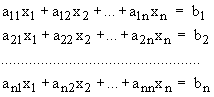
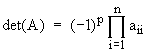
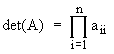
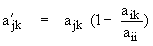
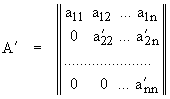
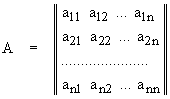Ðàçðàáîòêà áèáëèîòå÷íûõ ñðåäñòâ

ðåøåíèÿ çàäà÷ ëèíåéíîé àëãåáðû.

ÎÁÚÅÊÒ ÈÑÑËÅÄÎÂÀÍÈß: êëàññîâûå òèïû – ÷èñëåííàÿ êâàäðàòíàÿ ìàòðèöà è îäíîìåðíûé äèíàìè÷åñêèé ìàññèâ ñ ïåðåìåííûìè ðàçìåðàìè.

ÌÅÒÎÄ ÈÑÑËÅÄÎÂÀÍÈß: ðàçðàáîòêà àëãîðèòìîâ è íàïèñàíèå êëàññîâ ôóíêöèé íà ÿçûêå Borland Ñ++.

 êóðñîâîì ïðîåêòå ðàçðàáîòàíû àëãîðèòìû äëÿ ðåøåíèÿ îñíîâíûõ çàäà÷ ëèíåéíîé àëãåáðû. Ïî ýòèì àëãîðèòìàì íà ÿçûêå Borland C++ íàïèñàíû äâà êëàññà ôóíêöèé, îðèåíòèðîâàííûõ íà îáúåêòû òèïà ÷èñëåííàÿ êâàäðàòíàÿ ìàòðèöà è îäíîìåðíûé ìàññèâ (âåêòîð).  êëàññû âêëþ÷åíû àðèôìåòè÷åñêèå îïåðàöèè, îïåðàöèè ââîäà-âûâîäà, ôóíêöèè âû÷èñëåíèÿ îïðåäåëèòåëÿ ìàòðèöû, äëèíû âåêòîðà, à òàêæå ðåøåíèÿ ñèñòåìû ëèíåéíûõ àëãåáðàè÷åñêèõ óðàâíåíèé. Äëÿ íàãëÿäíîñòè ïîëó÷åííûõ ðåçóëüòàòîâ ðàçðàáîòàíà äåìîíñòðàöèîííî-òåñòèðóþùàÿ ïðîãðàììà.

Ðåçóëüòàòû êóðñîâîãî ïðîåêòà ìîãóò áûòü èñïîëüçîâàíû íà ïðàêòèêå äëÿ ðåøåíèÿ ñèñòåì ëèíåéíûõ óðàâíåíèé è äðóãèõ çàäà÷ ëèíåéíîé àëãåáðû.

ÂÂÅÄÅÍÈÅ

Îáúåêòíî-îðèåíòèðîâàííîå ïðîãðàììèðîâàíèå – ýòî íîâûé ñïîñîá ïîäõîäà ê ïðîãðàììèðîâàíèþ. Òàêîå ïðîãðàììèðîâàíèå, âçÿâ ëó÷øèå ÷åðòû ñòðóêòóðíîãî ïðîãðàììèðîâàíèÿ, äîïîëíÿåò åãî íîâûìè èäåÿìè, êîòîðûå ïåðåâîäÿò â íîâîå êà÷åñòâî ïîäõîä ê ñîçäàíèþ ïðîãðàìì.

Íàèáîëåå âàæíîå ïîíÿòèå ÿçûêîâ îáúåêòíî-îðèåíòèðîâàííîãî ïðîãðàììèðîâàíèÿ – ýòî ïîíÿòèå îáúåêòà (object). Îáúåêò – ýòî ëîãè÷åñêàÿ åäèíèöà, êîòîðàÿ ñîäåðæèò äàííûå è ïðàâèëà (ìåòîäû) îáðàáîòêè ýòèõ äàííûõ.  ÿçûêå Ñ++ â êà÷åñòâå òàêèõ ïðàâèë îáðàáîòêè âûñòóïàþò ôóíêöèè, ò. å. îáúåêò â Borland C++ îáúåäèíÿåò â ñåáå äàííûå è ôóíêöèè, îáðàáàòûâàþùèå ýòè äàííûå.

Îäíèì èç ñàìûõ ãëàâíûõ ïîíÿòèé ÿçûêà Ñ++ ÿâëÿåòñÿ ïîíÿòèå êëàññà (class).  ÿçûêå Ñ++ äëÿ òîãî, ÷òîáû îïðåäåëèòü îáúåêò, íàäî ñíà÷àëà îïðåäåëèòü åãî ôîðìó ñ ïîìîùüþ êëþ÷åâîãî ñëîâà class [1].

Áëèæàéøåé àíàëîãèåé êëàññà ÿâëÿåòñÿ ñòðóêòóðà. Ïàìÿòü âûäåëÿåòñÿ îáúåêòó òîëüêî òîãäà, êîãäà êëàññ èñïîëüçóåòñÿ äëÿ åãî ñîçäàíèÿ. Ýòîò ïðîöåññ íàçûâàåòñÿ ñîçäàíèåì ýêçåìïëÿðà êëàññà (class instance).

Ëþáîé îáúåêò ÿçûêà Ñ++ èìååò îäèíàêîâûå àòðèáóòû è ôóíêöèîíàëüíîñòü ñ äðóãèìè îáúåêòàìè òîãî æå êëàññà. Çà ñîçäàíèå ñâîèõ êëàññîâ è ïîâåäåíèå îáúåêòîâ ýòèõ êëàññîâ ïîëíóþ îòâåòñòâåííîñòü íåñåò ñàì ïðîãðàììèñò. Ðàáîòàÿ â íåêîòîðîé ñðåäå, ïðîãðàììèñò ïîëó÷àåò äîñòóï ê îáøèðíûì áèáëèîòåêàì ñòàíäàðòíûõ êëàññîâ.

Îáû÷íî, îáúåêò íàõîäèòñÿ â íåêîòîðîì óíèêàëüíîì ñîñòîÿíèè, îïðåäåëÿåìîì òåêóùèìè çíà÷åíèÿìè åãî àòðèáóòîâ. Ôóíêöèîíàëüíîñòü îáúåêòíîãî êëàññà îïðåäåëÿåòñÿ âîçìîæíûìè îïåðàöèÿìè íàä ýêçåìïëÿðîì ýòîãî êëàññà.

Øàáëîíû, èëè ïàðàìåòðèçîâàííûå òèïû, ïîçâîëÿþò êîíñòðóèðîâàòü ñåìåéñòâî ñâÿçàííûõ ôóíêöèé èëè êëàññîâ. Îáîáùåííûé ñèíòàêñèñ îïðåäåëåíèÿ øàáëîíà èìååò âèä

template <ñïèñîê øàáëîííûõ òèïîâ> {îáúÿâëåíèå} ;

Ðàçëè÷àþò øàáëîíû ôóíêöèé è øàáëîíû êëàññîâ.

Øàáëîí êëàññîâ çàäàåò îáðàçåö îïðåäåëåíèé ñåìåéñòâà êëàññîâ. Íàä òèïèçèðîâàííûìè ýëåìåíòàìè ýòîãî êëàññà âûïîëíÿþòñÿ îäèíàêîâûå áàçîâûå îïåðàöèè âíå çàâèñèìîñòè îò êîíêðåòíîãî òèïà ýëåìåíòîâ [2].

Ââåäåíèå â îáúåêòíî-îðèåíòèðîâàííîå ïðîãðàììèðîâàíèå

Îáúåêòíî-îðèåíòèðîâàííîå ïðîãðàììèðîâàíèå ïðåäñòàâëÿåò ñîáîé ÷óòü áîëåå àâòîìàòèçèðîâàííûé ñïîñîá ïðîãðàììèðîâàíèÿ. Îáúåêòíî-îðèåíòèðîâàííûå ïðîãðàììû – ýòî íå ïðîñòî ïðîöåäóðíûå ïðîãðàììû, ïåðåâåäåííûå íà íîâûé ñèíòàêñèñ. Îíè äîëæíû ñòðîèòñÿ íà íîâîé ôèëîñîôèè ðàçðàáîòêè. Äëÿ íèõ òðåáóåòñÿ íîâàÿ ñòðàòåãèÿ ïðîãðàììèðîâàíèÿ, êîòîðóþ ÷àñòî áûâàåò òðóäíî îñâîèòü [3].

Îñíîâíàÿ èäåÿ ÎÎÏ: ïðîãðàììà ñîñòîèò èç ãðóïïû îáúåêòîâ, ÷àñòî ñâÿçàííûõ ìåæäó ñîáîé.  Ñ++ îáúåêòû îïèñûâàþòñÿ ïðè ïîìîùè íîâîãî òèïà äàííûõ class. Êëàññ âêëþ÷àåò â ñåáÿ íàáîð ïåðåìåííûõ (äàííûõ) è îïåðàöèé (ìåòîäîâ èëè ôóíêöèé-÷ëåíîâ), êîòîðûå äåéñòâóþò íà ýòè ïåðåìåííûå. Ïîëó÷åííûìè îáúåêòàìè ìîæíî óïðàâëÿòü ïðè ïîìîùè ñîîáùåíèé.

 ÎÎÏ îáúåêòû âêëþ÷àþò â ñåáÿ íå òîëüêî äàííûå (äàííûå-÷ëåíû), íî è ìåòîäû (ôóíêöèè-÷ëåíû) âîçäåéñòâèÿ íà ýòè äàííûå. Ýòè äâå ÷àñòè â ñî÷åòàíèè îáðàçóþò ôóíêöèîíàëüíóþ åäèíèöó ïðîãðàììû. Äðóãèìè ñëîâàìè, îáúåêòû ñîäåðæàò äàííûå è ìåòîäû ðàáîòû ñ ýòèìè äàííûìè. Íèæå ïðèâåäåíû òðè îñíîâíûõ ïðåèìóùåñòâà îáúåêòíî-îðèåíòèðîâàííûõ ïðîãðàìì ïî ñðàâíåíèþ ñ ýêâèâàëåíòíûìè ïðîãðàììàìè, ðàçðàáîòàííûìè ñâåðõó âíèç.

Ñîïðîâîæäåíèå ïðîãðàììû. Ïðîãðàììû ïðîùå ÷èòàòü è ïîíèìàòü, ÎÎÏ ïîçâîëÿåò óïðàâëÿòü ñëîæíîñòüþ ïðîãðàììû, îñòàâëÿÿ âèäèìûìè ïðîãðàììèñòó òîëüêî ñóùåñòâåííûå äåòàëè.

Ìîäèôèêàöèÿ ïðîãðàììû (äîáàâëåíèå èëè èñêëþ÷åíèå âîçìîæíîñòåé). Âû ìîæåòå ÷àñòî äåëàòü äîïîëíåíèÿ èëè èñêëþ÷åíèÿ â ïðîãðàììå, íàïðèìåð ïðè ðàáîòå ñ áàçîé äàííûõ, ïðîñòî äîáàâëÿÿ è èñêëþ÷àÿ îáúåêòû. Íîâûå îáúåêòû ìîãóò íàñëåäîâàòü âñå ñâîéñòâà áàçîâûõ îáúåêòîâ, íåîáõîäèìî òîëüêî äîáàâèòü èëè óáðàòü îòëè÷àþùèåñÿ ñâîéñòâà.

Ïîâòîðíîå èñïîëüçîâàíèå. Ìîæíî ñîõðàíèòü ãðàìîòíî ðàçðàáîòàííûé îáúåêò â íàáîðå ïîëåçíûõ ïðîãðàìì è çàòåì âñòàâèòü åãî â íîâóþ ïðîãðàììó ñ íåáîëüøèìè èçìåíåíèÿìè èëè áåç èçìåíåíèé.

ÎÎÏ ïîëíîñòüþ ïðèíàäëåæèò ê ìèðó Ñ++, ïîñêîëüêó â Ñ íåò îñíîâíîãî ÿäðà – àáñòðàêòíîãî òèïà äàííûõ class [5]. Ïîýòîìó ïåðåïèñàòü ïðîöåäóðíî-îðèåíòèðîâàííóþ ïðîãðàììó êàê îáúåêòíî-îðèåíòèðîâàííóþ ãîðàçäî ñëîæíåå, ÷åì ïðîñòî ïîäñòàâèòü âìåñòî îäíîãî êëþ÷åâîãî ñëîâà äðóãîå.

ÎÎÏ ïðåäñòàâëÿåò ñîáîé òåõíèêó ïðîãðàììèðîâàíèÿ, êîòîðàÿ ïîçâîëÿåò ðàññìàòðèâàòü îñíîâíûå èäåè êàê ìíîæåñòâî îáúåêòîâ. Èñïîëüçóÿ îáúåêòû, ìîæíî ïðåäñòàâèòü çàäà÷è, êîòîðûå íåîáõîäèìî âûïîëíèòü, èõ âçàèìîäåéñòâèå è ëþáûå çàäàííûå óñëîâèÿ, êîòîðûå äîëæíû áûòü ñîáëþäåíû. Ñòðóêòóðà äàííûõ ÷àñòî îáðàçóåò îñíîâû îáúåêòîâ; òàêèì îáðàçîì â Ñ èëè Ñ++ òèï struct ìîæåò îáðàçîâûâàòü ýëåìåíòàðíûé îáúåêò. Ñâÿçü ñ îáúåêòîì ìîæíî îðãàíèçîâàòü ïðè ïîìîùè ñîîáùåíèé. Èñïîëüçîâàíèå ñîîáùåíèé ïîõîæå íà âûçîâ ôóíêöèé â ïðîöåäóðíî-îðèåíòèðîâàííîé ïðîãðàììå. Êîãäà îáúåêò ïîëó÷àåò ñîîáùåíèå, âñòóïàþò â äåéñòâèå ìåòîäû, ñîäåðæàùèåñÿ â îáúåêòå. Ìåòîäû (èõ èíîãäà íàçûâàþò ôóíöèÿìè-÷ëåíàìè) àíàëîãè÷íû ôóíêöèÿì ïðîöåäóðíî-îðèåíòèðîâàííîãî ïðîãðàììèðîâàíèÿ. Òåì íå ìåíåå ìåòîä ÿâëÿåòñÿ ÷àñòüþ îáúåêòà, à íå ÷åì-òî îòäåëüíûì, êàê áûëî áû â ïðîöåäóðíîì àíàëîãå.

Îñíîâíûå òåðìèíû è ïîëîæåíèÿ ÎÎÏ

Èíêàïñóëÿöèÿ äàííûõ

Ýòîò òåðìèí âêëþ÷àåò â ñåáÿ ëîãè÷åñêîå ñâÿçûâàíèå äàííûõ ñ êîíêðåòíîé îïåðàöèåé. Îíà òàê æå îçíà÷àåò, ÷òî îíè ÿâëÿþòñÿ íå -ãëîáàëüíûìè äîñòóïíûìè âñåé ïðîãðàììå, à ëîêàëüíûìè – äîñòóïíûìè òîëüêî ìàëîé åå ÷àñòè. Èíêàïñóëÿöèÿ òàêæå àâòîìàòè÷åñêè ïîäðàçóìåâàåò çàùèòó äàííûõ. Èìåííî äëÿ ýòîãî ïðåäíàçíà÷åíà ñòðóêòóðà class â Ñ++.  êëàññå óïðàâëåíèå ôóíêöèîíàëüíûìè äåòàëÿìè îáúåêòà îñóùåñòâëÿåòñÿ ïðè ïîìîùè ñïåöèôèêàòîðîâ private, public, protected.

Èåðàðõèÿ êëàññîâ

 îáùåì ñëó÷àå ìîæíî ïðåäñòàâèòü ñåáå èåðàðõèþ êëàññîâ êàê ðîäîñëîâíóþ â ãåíåàëîãè÷åñêîì äðåâå, ãäå êëàññ Ñ++ ïðåäñòàâëÿåò ñîáîé øàáëîí äëÿ ñîçäàíèÿ êëàññîâ-ïîòîìêîâ. Îáúåêòû, ïîëó÷åííûå èç îïèñàíèÿ êëàññà, íàçûâàþò ýêçåìïëÿðàìè ýòîãî êëàññà. Ìîæíî ñîçäàòü èåðàðõèþ êëàññîâ ñ êëàññîì-ðîäèòåëåì è íåñêîëüêèìè êëàññàìè-ïîòîìêàìè. Îñíîâîé äëÿ ýòîãî ÿâëÿþòñÿ ïðîèçâîäíûå êëàññû.

Íàñëåäîâàíèå

Íàñëåäîâàíèå â ÎÎÏ ïîçâîëÿåò êëàññó ïîëó÷àòü ñîâéñòâà äðóãîãî êëàññà îáúåêòîâ. Ðîäèòåëüñêèé êëàññ ñëóæèò øàáëîíîì äëÿ ïðîèçâîäíîãî êëàññà; ýòîò øàáëîí ìîæíî ìåíÿòü ðàçëè÷íûìè ñïîñîáàìè. Íàñëåäîâàíèå ÿâëÿåòñÿ âàæíûì ïîëîæåíèåì, ïîñêîëüêó îíî ïîçâîëÿåò ïîâòîðíî èñïîëüçîâàòü îïðåäåëåíèå êëàññà áåç çíà÷èòåëüíûõ èçìåíåíèé â êîäå.

Ïîëèìîðôèçì

Ñòðîèòñÿ íà îïèñàíîé âûøå êîíöåïöèè íàñëåäîâàíèÿ. Ïðîãðàììà ïîñûëàåò îäíî è òîæå ñîîáùåíèå êàê îáúåêòó ðîäèòåëüñêîãî êëàññà, òàê è âñåì îáúåêòàì ïðîèçâîäíûõ êëàññîâ. È ðîäèòåëüñêèé êëàññ, è êëàññû-ïîòîìêè îòâåòÿò íà ñîîáùåíèå ñîîòâåòñòâóþùèì îáðàçîì. Ïîëèìîðôèçì äàåò âîçìîæíîñòü äîïîëíÿòü óæå ñóùåñòâóþùèå ÷àñòè ïðîãðàììû.

Âèðòóàëüíûå ôóíêöèè

Âèðòóàëüíûå ôóíêöèè îïðåäåëÿþòñÿ â ðîäèòåëüñêîì êëàññå, à â ïðîèçâîäíûõ êëàññàõ ïðîèñõîäèò äîîïðåäåëåíèå ýòèõ ôóíêöèé è äëÿ íèõ ñîçäàþòñÿ íîâûå ðåàëèçàöèè. Ïðè ðàáîòå ñ âèðòóàëüíûìè ôóíêöèÿìè ñîîáùåíèÿ ïåðåäàþòñÿ êàê óêàçàòåëè, êîòîðûå óêàçûâàþò íà îáúåêò âìåñòî ïðÿìîé ïåðåäà÷è îáúåêòó. Âèðòóàëüíûå ôóíêöèè èñïîëüçóþò òàáëèöó äëÿ àäðåñíîé èíôîðìàöèè. Ýòà òàáëèöà èíèöèàëèçèðóåòñÿ âî âðåìÿ âûïîëíåíèÿ ïðè ïîìîùè êîíñòðóêòîðà.

Êîíñòðóêòîð âûçûâàåòñÿ êàæäûé ðàç, êîãäà ñîçäàåòñÿ îáúåêò åãî êëàññà. Çàäà÷à êîíñòðóêòîðà â äàííîì ñëó÷àå ñîñòîèò â ñâÿçûâàíèè âèðòóàëüíîé ôóíêöèè ñ òàáëèöåé àäðåñíîé èíôîðìàöèè. Âî âðåìÿ êîìïèëÿöèè àäðåñ âèðòóàëüíîé ôóíêöèè íåèçâåñòåí; âìåñòî ýòîãî åé îòâîäèòñÿ ïîçèöèÿ â òàáëèöå àäðåñîâ. Ýòà ïîçèöèÿ áóäåò ñîäåðæàòü àäðåñ ôóíêöèè [5].

Ãëàâà 2. Çàäà÷è ëèíåéíîé àëãåáðû

2.1. Âû÷èñëåíèå îïðåäåëèòåëåé

Ïóñòü èìååì êâàäðàòíóþ ìàòðèöó ðàçìåðîì n´ n:

. (2.1.1)

Òðåáóåòñÿ âû÷èñëèòü îïðåäåëèòåëü ìàòðèöû det(A).

Ýêâèâàëåíòíûì ïðåîáðàçîâàíèåì ìàòðèöû íàçûâàþò ïðåîáðàçîâàíèÿ ìàòðèöû, íå èçìåíÿþùèå âåëè÷èíó îïðåäåëèòåëÿ ìàòðèöû. Ýêâèâàëåíòíûì ÿâëÿåòñÿ ñëåäóþùåå ïðåîáðàçîâàíèå: ëþáóþ ñòðîêó ìàòðèöû ìîæíî çàìå-íèòü ñóììîé èñõîäíîé ñòðîêè è ëþáîé äðóãîé, óìíîæåííîé íà ëþáîå ÷èñëî, íå ðàâíîå íóëþ.

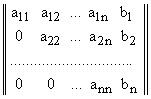
Èñïîëüçóÿ òàêîãî ðîäà ïðåîáðàçîâàíèÿ ìîæíî ïîïûòàòüñÿ ïðèâåñòè èñ-õîäíóþ ìàòðèöó ê òðåóãîëüíîìó âèäó:

,

ïðè ýòîì det(A) = det(A¢ ).

Ôîðìóëà äëÿ ïåðåñ÷åòà ýëåìåíòîâ ìàòðèöû èìååò âèä:

, (2.1.2)

ãäåi- íîìåð ñòîëáöà, â êîòîðîì ýëåìåíòû, ëåæàùèå íèæå ãëàâíîé
äèàãîíàëè, ïðåâðàùàþòñÿ â íóëè;

j- íîìåð ýëåìåíòà â îáðàáàòûâàåìîì ñòîëáöå (ò.å. íîìåð ñòðîêè);

k- íîìåð ýëåìåíòà â òåêóùåé ñòðîêå.

Àëãîðèòì ïðèâåäåíèÿ ìàòðèöû ê òðåóãîëüíîìó âèäó âêëþ÷àåò â ñåáÿ 3 âëîæåííûõ öèêëà:

- âíåøíèé öèêë, i = 1 .. n-1 ;

- ñðåäíèé öèêë, j = i+1 .. n ;

- âíóòðåííèé öèêë, k = i+1 .. n .

Òåïåðü èñêîìûé îïðåäåëèòåëü âû÷èñëÿåòñÿ êàê ïðîèçâåäåíèå äèàãîíàëüíûõ ýëåìåíòîâ:

.

Îïèñàííûé âûøå àëãîðèòì äàåò ðåçóëüòàò íå âñåãäà. Åñëè ïðè âûïîëíåíèè i-òîãî øàãà âíåøíåãî öèêëà äèàãîíàëüíûé ýëåìåíò aii îêàçûâàåòñÿ ðàâíûì íóëþ, à ñðåäè ýëåìåíòîâ i-òîãî ñòîëáöà ñ íîìåðàìè îò i+1 äî n åñòü õîòÿ áû îäèí íå íóëåâîé, àëãîðèòì çàâåðøàåòñÿ áåçðåçóëüòàòíî (èç-çà íåâîçìîæíîñòè âû÷èñëåíèé ïî ôîðìóëå (2.1.2). Äëÿ òîãî, ÷òîáû ýòî íå ïðîèñõîäèëî, èñïîëüçóåòñÿ ïðèåì, êîòîðûé íàçûâàåòñÿ “âûáîð ãëàâíîãî ýëåìåíòà”.

Ïðè âûïîëíåíèè î÷åðåäíîãî øàãà öèêëà ïî i ïðåäâàðèòåëüíî âûïîëíÿþòñÿ ñëåäóþùèå îïåðàöèè:

1) íàõîäèòñÿ ìàêñèìàëüíûé ïî ìîäóëþ ýëåìåíò ñðåäè ýëåìåíòîâ i-òîãî ñòîëáöà îò aii äî ani ;

2) åñëè íàéäåííûé ýëåìåíò ali ðàâåí íóëþ, ïðîöåññ âû÷èñëåíèÿ çàâåðøàåòñÿ ñ âûäà÷åé ðåçóëüòàòà det(A) = 0 ;

3) åñëè l¹ i , òîãäà ñòðîêè èñõîäíîé ìàòðèöû ñ íîìåðàìè i,l ïîìåíÿòü ìåñòàìè.

Ïîñëå çàâåðøåíèÿ ïðåîáðàçîâàíèÿ ìàòðèöû, îïðåäåëèòåëü âû÷èñëÿåòñÿ ïî ôîðìóëå:

,

ãäå p – ÷èñëî âûïîëíåííûõ îïåðàöèé ïåðåìåíû ñòðîê ìåñòàìè.

 

2.2 Îáðàùåíèå ìàòðèö

Îáðàòíîé ê ìàòðèöå A íàçûâàåòñÿ ìàòðèöà A-1, îáëàäàþùàÿ ñâîéñòâîì:

A× A-1 = A-1× A = I ,

ãäå I – åäèíè÷íàÿ äèàãîíàëüíàÿ ìàòðèöà. Îïèøåì îäèí èç óíèâåðñàëüíûõ è ýôôåêòèâíûõ ìåòîäîâ ðàñ÷åòà îáðàòíîé ìàòðèöû (ìåòîä Æîðäàíà-Ãàóññà, â êíèãå [4-218] îïèñàí êàê “ìåòîä èñêëþ÷åíèé”).  [5-22] ïðèâåäåí áîëåå ýôôåêòèâíûé ïî ïàìÿòè àëãîðèòì îáðàùåíèÿ ìàòðèöû.

Ïóñòü èìååì ìàòðèöó A âèäà (2.1.1) è ïóñòü B – åäèíè÷íàÿ äèàãîíàëüíàÿ ìàòðèöà òàêîãî æå ðàçìåðà. Ñîçäàäèì ðàáî÷óþ ìàòðèöó R ðàçìåðîì N´ 2N ïðîñòî ïðèñîåäèíèâ ìàòðèöó B ñïðàâà ê ìàòðèöå A :

.

Íàä ñòðîêàìè òàêîé ðàñøèðåííîé ìàòðèöû áóäåì ïðîèçâîäèòü ïðåîáðàçîâàíèÿ, àíàëîãè÷íûå òåì, êîòîðûå áûëè îïèñàíû â ï.2.1. Ëåâóþ ÷àñòü ìàòðèöû R áóäåì íàçûâàòü ïîäìàòðèöåé A, ïðàâóþ – ïîäìàòðèöåé B. Âåñü ïðîöåññ ïðåîáðàçîâàíèÿ ìàòðèöû R ðàçîáüåì íà 3 ýòàïà.

1 ýòàï. Âûïîëíèì ïðåîáðàçîâàíèÿ ñòðîê ìàòðèöû òàê, ÷òîáû âñå ýëåìåíòû, ëåæàùèå íèæå äèàãîíàëüíûõ ýëåìåíòîâ ïîäìàòðèöû A, îáðàòèëèñü â íóëè. Ïðè ýòîì ìîæåò èñïîëüçîâàòüñÿ âûáîð ãëàâíîãî ýëåìåíòà.

2 ýòàï. Âûïîëíèì ïðåîáðàçîâàíèÿ òàê, ÷òîáû âñå ýëåìåíòû, ëåæàùèå âûøå äèàãîíàëüíûõ ýëåìåíòîâ ïîäìàòðèöû A, îáðàòèëèñü â íóëè. Ïðåîáðàçîâàíèÿ íàäî âûïîëíÿòü â îáðàòíîì ïîðÿäêå: ñî ñòîëáöà íîìåð n è äî ñòîëáöà íîìåð 2.

3 ýòàï. Êàæäóþ ñòðîêó ðàñøèðåííîé ìàòðèöû R ñ íîìåðîì i äåëèì íà äèàãîíàëüíûé ýëåìåíò aii .

Ïîñëå çàâåðøåíèÿ ïðîöåäóðû ïîäìàòðèöà A ïðåâðàùàåòñÿ â åäèíè÷íóþ äèàãîíàëüíóþ ìàòðèöó, à ïîäìàòðèöà B áóäåò ðàâíà èñêîìîé îáðàòíîé ìàòðèöå A-1 . Àëãîðèòì èìååò ïîðÿäîê O(n3).

2.3. Ìåòîäû ðåøåíèÿ ñèñòåì ëèíåéíûõ óðàâíåíèé

Çàäà÷à ïîèñêà ðåøåíèé ñèñòåìû ëèíåéíûõ óðàâíåíèé èìååò íå òîëüêî ñàìîñòîÿòåëüíîå çíà÷åíèå, íî ÷àñòî ÿâëÿåòñÿ ñîñòàâíîé ÷àñòüþ àëãîðèòìà ðåøåíèÿ ìíîãèõ íåëèíåéíûõ çàäà÷. Îñíîâíûå ìåòîäû ðåøåíèÿ ÑËÓ:

- ìåòîä Ãàóññà;

- ìåòîä îáðàùåíèÿ ìàòðèöû;

- èòåðàöèîííûå ìåòîäû.

2.4. Ìåòîä Ãàóññà

Ïóñòü èìååì ñèñòåìó ëèíåéíûõ óðàâíåíèé:

Ïðîñòîé ìåòîä Ãàóññà ñîñòîèò â ñëåäóþùåì.

Ñîñòàâèì ðàñøèðåííóþ ìàòðèöó, ïðèïèñàâ ê ìàòðèöå êîýôôèöèåíòîâ ÑËÓ äîïîëíèòåëüíûé ñòîëáåö – ïðàâûå ÷àñòè óðàâíåíèÿ:

.

Âûïîëíèì íàä ñòðîêàìè ðàñøèðåííîé ìàòðèöû ïðåîáðàçîâàíèÿ, àíàëîãè÷íûå òåì, êîòîðûå áûëè îïèñàíû â ï. 2.1:

,

,

è ïðèâåäåì åå ê òðåóãîëüíîìó âèäó:

.

Òåïåðü ìîæíî âû÷èñëèòü èñêîìûå âåëè÷èíû xi , íà÷èíàÿ ñ ïîñëåäíåãî, ò.å. âíà÷àëå íàõîäèòñÿ xn , çàòåì xn-1, xn-2, … , x1. Ôîðìóëà äëÿ âû÷èñëåíèé èìååò âèä:

.

Äëÿ ðàñøèðåíèÿ âîçìîæíîñòåé è ïîâûøåíèÿ óñòîé÷èâîñòè ïðèâåäåííîãî àëãîðèòìà èñïîëüçóåòñÿ âûáîð ãëàâíîãî ýëåìåíòà. Ïîðÿäîê ìåòîäà Ãàóññà ðàâåí O(n3).

2.5. Ìåòîä îáðàùåíèÿ ìàòðèöû

Ïðåäñòàâèì ñèñòåìó ëèíåéíûõ óðàâíåíèé â ìàòðè÷íîé ôîðìå:

.

Óìíîæèì ïîñëåäíåå ðàâåíñòâî ñëåâà íà A-1 :

.

Ó÷èòûâàÿ, ÷òî A-1× A = I , ôîðìàëüíî ïîëó÷àåì èñêîìîå ðåøåíèå:

Òàêèì îáðàçîì, ðåøåíèå ñèñòåìû âûïîëíÿåòñÿ â äâà ýòàïà:

1) âû÷èñëåíèå îáðàòíîé ìàòðèöû;

2) óìíîæåíèå îáðàòíîé ìàòðèöû íà âåêòîð ïðàâûõ ÷àñòåé ÑËÓ.

Íåñìîòðÿ íà òî, ÷òî ìåòîä îáðàùåíèÿ ìàòðèöû èìååò òàêîé æå ïîðÿäîê, êàê è ìåòîä Ãàóññà - O(n3), ïî îáúåìó âû÷èñëåíèé îí ïðîèãðûâàåò åìó â íåñêîëüêî ðàç. Îäíàêî, åñëè ÑËÓ íåîáõîäèìî ðåøàòü ìíîãîêðàòíî è ïðè ýòîì èçìåíÿåòñÿ ëèøü âåêòîð ïðàâûõ ÷àñòåé, ìåòîä îáðàùåíèÿ ìàòðèöû ñòàíîâèòñÿ âñå æå âûãîäíûì.

Ïðàêòè÷åñêàÿ ÷àñòü

Îïèñàíèå êëàññà Matrix äëÿ ðåøåíèÿ çàäà÷ ëèíåéíîé àëãåáðû

Êëàññ èìååò ïðèâàòíûå è îáùåäîñòóïíûå ÷ëåíû-äàííûå è ÷ëåíû-ôóíêöèè (ìåòîäû). Äëÿ õðàíåíèÿ êîìïîíåíòîâ ìàòðèöû èñïîëüçóåòñÿ îäíîìåðíûé äèíàìè÷åñêèé ìàññèâ ýëåìåíòîâ òèïà ïàðàìåòðà øàáëîíà. Äëÿ ñîçäàíèÿ îáúåêòà ïðåäóñìîòðåíû òðè êîíñòðóêòîðà: êîíñòðóêòîð ïî óìîë÷àíèþ, êîíñòðóêòîð ñ ïàðàìåòðàìè, êîíñòðóêòîð êîïèðîâàíèÿ è äåñòðóêòîð. Äëÿ âûïîëíåíèÿ ìíîæåñòâà ìàòðè÷íûõ îïåðàöèé ñîçäàíû ïåðåãðóæåííûå îïåðàöèè: ïðèñâàèâàíèÿ (=), ñëîæåíèÿ (+), âû÷èòàíèÿ (-), óìíîæåíèÿ(*) è ò.ï. Íà áàçå îïåðàòîðîâ ââîäà/âûâîäà Ñ++ ðàçðàáîòàíû ôóíêöèè ââîäà ìàòðèö èç ïîòîêà è âûâîäà èõ â ïîòîê, ïðåäóñìàòðèâàþùèå â ñëó÷àå ôàéëîâîãî ââîäà/âûâîäà êàê òåêñòîâóþ ôîðìó õðàíåíèÿ, òàê è áèíàðíóþ.

Äîñòóï ê ÷ëåíàì-äàííûì êëàññà – ÷èñëó ñòðîê è ñòîëáöîâ ìàòðèöû îñóùåñòâëÿåòñÿ ñ ïîìîùüþ ìåòîäîâ size_row( ) è size_col( ). Äëÿ äîñòóïà ê ýëåìåíòàì ìàòðèöû ñîçäàí ïåðåãðóæåííûé îïåðàòîð âûçîâà ôóíêöèè operator( ) (dim x, dim x), ãäå dim – ïåðåîïðåäåëåííûé òèï unsigned char. Âûçîâ ôóíêöèè èñïîëüçóåòñÿ êàê îïåðàòîð èíäåêñèðîâàíèÿ, ïðèíèìàþùèé äâà àðãóìåíòà. Àíàëîãè÷íî ñîçäàí îïåðàòîð âûçîâà ôóíêöèè ñ îäíèì àðãóìåíòîì operator( ) (dim x). Äëÿ äàííîãî êëàññà – ýòî î÷åíü âàæíûå ïåðåãðóæåííûå îïåðàòîðû, ò.ê. îíè èñïîëüçóþòñÿ âî âñåõ ôóíêöèÿõ è îïåðàòîðàõ, â êîòîðûõ ïðîèñõîäèò îáðàùåíèå ê ýëåìåíòàì ìàòðèöû.

Îïèñàíèå ôóíêöèé, êîíñòðóêòîðîâ è äåñòðóêòîðîâ êëàññà:

Êîíñòðóêòîð ïî óìîë÷àíèþ Matrix( ):

Êîíñòðóêòîð ïî óìîë÷àíèþ ñîçäàåò ìàòðèöó íóëåâîãî ðàçìåðà.  äàëüíåéøåì ðàçìåð ýòîé ìàòðèöû ìîæíî èçìåíèòü ñ ïîìîùüþ ôóíêöèè newsize(i, j).

Êîíñòðóêòîð ñ ïàðàìåòðàìè Matrix(dim, dim=1):

Ýòî îáû÷íûé êîíñòðóêòîð ñ ïàðàìåòðàìè, êîòîðûé ïðèíèìàåò â êà÷åñòâå ïàðàìåòðîâ ðàçìåðû ìàòðèöû è ñîçäàåò îäíîìåðíûé äèíàìè÷åñêèé ìàññèâ ðàçìåðîì m*n, ãäå m – ÷èñëî ñòðîê, à n – ÷èñëî ñòîëáöîâ ìàòðèöû. Ñ öåëüþ âîçìîæíîñòè èñïîëüçîâàòü åãî äëÿ ñîçäàíèÿ âåêòîðîâ, âòîðîé ïàðàìåòð êîíñòðóêòîðà çàäàí êàê óìàë÷èâàåìûé ñî çíà÷åíèåì 1. Äëÿ ïåðâîíà÷àëüíîé “èíèöèàëèçàöèè” ýëåìåíòîâ ìàòðèöû íóëÿìè èñïîëüçóåòñÿ ôóíêöèÿ setmem( ).

Êîíñòðóêòîð êîïèðîâàíèÿ Matrix(const Matrix &):

Êîíñòðóêòîð ïðèíèìàåò â êà÷åñòâå ïàðàìåòðà ññûëêó íà îáúåêò êëàññà (íà ñóùåñòâóþùóþ ìàòðèöó), îïðåäåëÿåò åå ðàçìåð, âûäåëÿåò äëÿ íåå ïàìÿòü è êîïèðóåò â ýòó ïàìÿòü ñîäåðæèìîå ìàòðèöû, ïðèíèìàåìîé ïî ññûëêå. Òàêèì îáðàçîì, ñîçäàåòñÿ òî÷íàÿ êîïèÿ ìàòðèöû ñ òåêóùèìè çíà÷åíèÿìè åå ýëåìåíòîâ.

Äåñòðóêòîð ~Matrix( ):

Äåñòðóêòîð âûñâîáîæäàåò ïàìÿòü, âûäåëåííóþ êîíñòðóêòîðàìè äëÿ ýëåìåíòîâ ìàòðèöû.

Ôóíêöèÿ îïåðàöèè ïðèñâàèâàíèÿ "=" Matrix& operator= (Matrix&):

Äàííàÿ ôóíêöèÿ ñðàâíèâàåò àäðåñ ïåðåäàâàåìîãî ïî ññûëêå îáúåêòà ñ àäðåñîì ñîáñòâåííîãî êëàññà, ÷òîáû íå ïðåäïðèíÿëàñü ïîïûòêà ïðèñâîèò îáúåêò ñàìîìó ñåáå. Ïîñëå ýòîãî ñîçäàåòñÿ íîâûé ìàññèâ ñ ÷èñëîì ýëåìåíòîâ, ðàâíûì ÷èñëó ýëåìåíòîâ ìàññèâà ïðèíèìàåìîãî ïî ññûëêå, è â ýòîò ìàññèâ çàíîñèòñÿ ñîäåðæèìîå ïðèíèìàåìîãî ìàññèâà. Âîçâðàùàåòñÿ ðàçûìåíîâàííûé óêàçàòåëü this (return *this;).

Ôóíêöèè îïåðàöèé ñóììèðîâàíèÿ, âû÷èòàíèÿ, óìíîæåíèÿ ìàòðèö è óìíîæåíèÿ ìàòðèöû íà ÷èñëî:

Ýòè ôóíêöèè ðåàëèçîâàíû êàê äðóæåñòâåííûå ôóíêöèè è àëãîðèòìû ýòèõ ôóíêöèé àíàëîãè÷íû ïî ñâîåìó ñîñòàâó. Îáùèé âèä ïðîòîòèïà ýòèõ ôóíêöèé: friend Matrix operator @(const Matrix&, const Matrix&). Ïðèìåíåíèå äðóæåñòâåííûõ ôóíêöèé â äàííîì ñëó÷àå öåëåñîîáðàçíî äëÿ òîãî, ÷òîáû èìåòü âîçìîæíîñòü ïåðåäàâàòü â îïåðàòîð ôóíêöèþ îáúåêòû â ëþáîé ïîñëåäîâàòåëüíîñòè.  ýòèõ îïåðàòîðàõ-ôóíêöèÿõ âíà÷àëå ñîçäàåòñÿ âðåìåííûé îáúåêò òèïà ìàòðèöà (ñ ïîìîùüþ êîíñòðóêòîðà êîïèðîâàíèÿ), â êîòîðûé êîïèðóåòñÿ ïåðâàÿ ìàòðèöà è êîòîðûé ïðè âûõîäå èç ôóíêöèè ÿâëÿåòñÿ âîçâðàùàåìûì îáúåêòîì. Çàòåì ýòà ìàòðèöà ñóììèðóåòñÿ (âû÷èòàåòñÿ, óìíîæàåòñÿ) ñ ìàòðèöåé, ñòîÿùåé ïîñëå çíàêà îïåðàòîðà ïî ñîîòâåòñòâóþùèì ïðàâèëàì ìàòðè÷íûõ îïåðàöèé. Ïðè ýòîì äëÿ äîñòóïà ê ýëåìåíòàì ìàòðèöû è èíäåêñèðîâàíèÿ èñïîëüçóþòñÿ ïåðåãðóæåííûå îïåðàòîðû âûçîâà ôóíêöèè operator( ) (dim x, dim x) è operator( ) (dim x).

Ôóíêöèÿ – îïåðàòîð Matrix operator^ (int):

Ýòîò îïåðàòîð-ôóíêöèÿ ðåàëèçîâàí êàê ÷ëåí êëàññà è ïðåäíàçíà÷åí äëÿ âîçâåäåíèÿ ìàòðèöû â ñòåïåíü.  ñëó÷àå, êîãäà çíà÷åíèå âõîäíîãî ïàðàìåòðà ðàâíî ìèíóñ åäèíèöå îñóùåñòâëÿåòñÿ âûçîâ ôóíêöèè âû÷èñëåíèÿ îáðàòíîé ìàòðèöû ìåòîäîì ïðåîáðàçîâàíèé Ãàóññà, äëÿ ÷åãî ðàçðàáîòàíà îòäåëüíàÿ ôóíêöèÿ Matrix & Gauss(dim, dim). Òàêèì îáðàçîì, èñïîëüçîâàíèå ýòîãî îïåðàòîðà ïîçâîëÿåò ðåøàòü ñèñòåìó ëèíåéíûõ àëãåáðàè÷åñêèõ óðàâíåíèé â ïðåäñòàâëåíèè X = (A^-1)*B, ãäå X è B –âåêòîðà íåèçâåñòíûõ è ïðàâûõ ÷àñòåé ñîîòâåòñòâåííî.

Ôóíêöèÿ – îïåðàòîð Matrix operator ! ( ):

Îïåðàòîð äëÿ îïðåäåëåíèÿ òðàíñïîíèðîâàííîé ìàòðèöû.

Ôóíêöèÿ – îïåðàòîð friend VARTYPE operator %(const Matrix&, const Matrix&):

Ôóíêöèÿ âû÷èñëåíèÿ ñêàëÿðíîãî ïðîèçâåäåíèÿ âåêòîðîâ.  íåé â íà÷àëå ïðîâåðÿåòñÿ, ÿâëÿþòñÿ ëè ïåðåäàâàåìûå îáúåêòû âåêòîðàìè, à çàòåì âû÷èñëÿåòñÿ ñêàëÿðíîå ïðîèçâåäåíèå.

Ôóíêöèè-÷ëåíû VARTYPE determ( ) è VARTYPE vmodule( ):

Ïåðâàÿ ôóíêöèÿ âû÷èñëÿåò îïðåäåëèòåëü ñîáñòâåííîãî îáúåêòà (ìàòðèöû). Ïðè ýòîì èñïîëüçóþòñÿ ôóíêöèÿ Matrix & Gauss(dim, dim). Ôóíêöèÿ VARTYPE vmodule( ) âû÷èñëÿåò äëèíó (ìîäóëü) âåêòîðà

Ôóíêöèÿ îïåðàöèè âûâîäà friend ostream& operator<<(ostream&, Matrix&):

Äàííàÿ ôóíêöèÿ íå ìîæåò áûòü ÷ëåíîì êëàññà, ïîýòîìó ÷òîáû èìåòü äîñòóï ê ïðèâàòíûì ýëåìåíòàì êëàññà, îíà îáúÿâëåíà "äðóæåñòâåííîé" ôóíêöèåé. Îíà èìååò äâà ïàðàìåòðà: ññûëêó íà ïîòîê, êîòîðûé íàõîäèòñÿ ñëåâà îò çíàêà îïåðàöèè <<, è ññûëêó íà îáúåêò, êîòîðûé íàõîäèòñÿ ñëåâà îò çíàêà îïåðàöèè, äàííûå ýòîãî îáúåêòà è áóäóò âûâîäèòüñÿ. Çàòåì ñëåäóåò ôîðìàòèðîâàííûé âûâîä â ïîòîê âñåõ ýëåìåíòîâ ìàññèâà è âîçâðàùàåòñÿ ïîòîê. Åñëè òðåáóåòñÿ âûâåñòè äàííûå â ôàéë, íóæíî îòêðûòü åãî ïðèñîåäèíåíèåì ê ïîòîêó ofstream.

Ôóíêöèÿ îïåðàöèè ââîäà friend istream& operator>>(istream&, Matrix&):

Òàê æå êàê è ïðåäûäóùàÿ, äàííàÿ ôóíêöèÿ íå ìîæåò áûòü ÷ëåíîì êëàññà, à ïîýòîìó äëÿ äîñòóïà ê ïðèâàòíûì ýëåìåíòàì êëàññà îáúÿâëåíà "äðóæåñòâåííîé" ôóíêöèåé êëàññà. Îíà òàê æå èìååò äâà ïàðàìåòðà: ññûëêó íà ïîòîê, êîòîðûé íàõîäèòñÿ ñëåâà îò çíàêà >>, è ññûëêó îáúåêò, êîòîðûé íàõîäèòñÿ ñëåâà îò çíàêà îïåðàöèè, â íåãî è áóäóò ââîäèòüñÿ äàííûå èç ïîòîêà. Çàòåì ñëåäóåò ââîä äàííûõ èç ïîòîêà â ýëåìåíòû ìàññèâà è âîçâðàùàåòñÿ ïîòîê. Äëÿ ââîäà äàííûõ èç ôàéëà, íóæíî îòêðûòü åãî ïðèñîåäèíåíèåì ê ïîòîêó ifstream.

Ôóíêöèè-÷ëåíû dim write(ofstream&) è dim read(ifstream&):

Ôóíêöèè ïðåäíàçíà÷åíû äëÿ âûâîäà â ôàéë è ââîäà èç ôàéëà ìàòðèö â èç äâîè÷íîì ïðåäñòàâëåíèè. Äëÿ ýòîãî íåîáõîäèìî ïåðåäàòü â íèõ ñîîòâåòñòâóþùóþ ññûëêó íà îòêðûòûé ôàéë.

Ôóíêöèÿ void ERROR_MATRIX(dim):

Ýòî ôóíêöèÿ-÷ëåí, êîòîðàÿ âûçûâàåòñÿ äëÿ ôèêñàöèè íåêîòîðûõ îøèáîê ïðè ñîçäàíèè ìàòðèö è ðàáîòå ñ íèìè, òàêèõ êàê îòñóòñòâèå ïàìÿòè, íåñîãëàñîâàííîñòü ðàçìåðîâ ìàòðèö ïðè îïåðàöèè óìíîæåíèÿ, ïîïûòêè âû÷èñëèòü îòðèöàòåëüíóþ ñòåïåíü ìàòðèöû è ò.ï.

Ëèñòèíã ìîäóëÿ ñ îïðåäåëåíèåì è ðåàëèçàöèåé êëàññà ìàòðèö

// ôàéë tmatr.cpp

#include

#include // äëÿ setmem()

#include

#include

typedef unsigned char dim;

template class Matrix {

typedef Matrix Vector;

private:

VARTYPE *matr; // óêàçàòåëü íà ìàññèâ ìàòðèöû

dim m,n;// ðàçìåðû ìàòðèöû

public:

// êîíñòðóêòîðû è äåñòðóêòîðû:

Matrix() { matr=(VARTYPE*)0; m=n=0; }

Matrix(dim,dim=1); // Îáû÷íûé êîíñòðóêòîð

Matrix(const Matrix&); // Êîíñòðóêòîð êîïèðîâàíèÿ

~Matrix() { delete [ ]matr; }

// äîñòóï ê ýëåìåíòàì ìàòðèöû

dim size_row() { return m; }// ÷èñëî ñòðîê

dim size_col() { return n; }// ÷èñëî ñòîëáöîâ

VARTYPE& operator() (dim x) const { return (*this)(x,0); }// ýëåìåíòó

// ïåðåãðóæåííûå îïåðàöèè è ôóíêöèè:

Matrix& operator=(const Matrix&);

Matrix& operator=(const VARTYPE&);

Matrix operator^(int); // âîçâåäåíèå â ñòåïåíü

Matrix operator!(); // òðàíñïîíèðîâàíèå

VARTYPE determ(); // îïðåäåëèòåëü ìàòðèöû

VARTYPE vmodul(); // ìîäóëü âåêòîðà

Matrix& Gauss(dim,dim); // ïðåîáðàçîâàíèå ïî Ãàóññó

// (äëÿ ïîëó÷. îáðàòíîé è åäèíè÷íîé ìàòðèöû)

// (äëÿ ïîëó÷. âåðõíåòðåóãîëüíîé ìàòðèöû)

Matrix minor(dim,dim); // âîçâðàùàåò óêàç. ìèíîð ìàòðèöû

Vector line(dim i) // âîçâðàùàåò âåêòîð-ñòðîêó ìàòðèöû

{ return extract(1,n,i,0); }

Vector column(dim j) // âîçâðàùàåò âåêòîð-ñòîëáåö ìàòðèöû

{ return extract(m,1,0,j); }

VARTYPE& operator() (dim,dim) const;// äîñòóï ê

Matrix& operator<<=(const Matrix &A) { return newsize(A.m,A.n)=A; }

// áåçóñëîâíîå ïðèðàâíèâàíèå ìàòðèö

Matrix& insert(const Matrix&, dim=0, dim=0);// âñòàâèòü ÷àñòü ìàòðèöû

Matrix extract(dim, dim, dim=0, dim=0);// èçâëå÷ü ÷àñòü ìàòðèöû

Matrix& newsize(dim, dim=1);// óñòàíîâèòü íîâûå ðàçìåðû

void swap_line(dim, dim);//îáìåí ñòðîêàìè ìàòðèöû

void swap_column(dim, dim);// îáìåí ñòîëáöàìè ìàòðèöû

friend Matrix operator+(const Matrix&,const Matrix&);//A-B

friend Matrix operator-(const Matrix&,const Matrix&);//A-B

friend Matrix operator*(const Matrix&,const Matrix&);//A*B

friend Matrix operator*(const double&,const Matrix&); //k*A

friend Matrix operator*(const Matrix&, const double&); //A*k

friend ostream& operator<<(ostream&,Matrix&);

// ïîòîêîâûé âûâîä ìàòðèöû

friend int operator>>(istream&,Matrix&);

// ïîòîêîâûé ââîä ñóùåñòâ. ìàòðèöû

// 0 - áåç. îøèáîê, 1 - áûëà îøèáêà

dim read(ifstream&); // ôàéëîâîå ÷òåíèå è çàïèñü ìàòðèöû

dim write(ofstream&);// â åå âíóòðåííåì, äâîè÷íîì ïðåäñòàâëåíèè.

friend VARTYPE operator %(const Matrix&,const Matrix&);

//Ôóíêöèÿ îøèáîê

void ERROR_MATRIX(dim) const;

};

// Ðåàëèçàöèÿ êëàññà ìàòðèö

template

Matrix::Matrix(dim M, dim N)

{

m=M;

n=N;

matr=new VARTYPE[m*n];

if(!matr) ERROR_MATRIX(1);

setmem(matr,sizeof(VARTYPE)*m*n,0);

}

template

Matrix::Matrix(const Matrix &M_Obj) //Êîíñòðóêòîð êîïèðîâàíèÿ

{

m=M_Obj.m;

n=M_Obj.n;

matr=new VARTYPE[m*n];

if(!matr) ERROR_MATRIX(1);

movmem(M_Obj.matr, matr, sizeof(VARTYPE)*m*n);

}

template

Matrix& Matrix::operator=(const Matrix &M_Obj)

{

m=M_Obj.m;

n=M_Obj.n;

matr=new VARTYPE[m*n];

if(!matr) ERROR_MATRIX(1);

movmem(M_Obj.matr,matr,sizeof(VARTYPE)*m*n);

return *this;

}

//Äèàãîíàëü?

template

Matrix& Matrix::operator=(const VARTYPE &f)

{

for(int i=0,j;i

if(i==j) (*this)(i,j)=f;

else (*this)(i,j)=0;

return *this;

}

template

Matrix Matrix::operator^(int q) // Ñòåïåíü

{

if (q>0)

{

for(Matrix M=*this; q>1; q--)

M=M*(*this);

return M;

}

if (q!=-1) ERROR_MATRIX(3);

// âû÷èñëåíèå îáðàòíîé ìåòoäîì ïðåîáðàçîâàíèé Ãàóññà

if (n!=m) ERROR_MATRIX(4);

Matrix M(m,2*n);

M.insert(*this);

for(int i=0;i

M(i,i+M.m)=1;

for(i=0;i

M.Gauss(i,i);

return M.extract(M.m,M.m,0,M.m);

}

template

Matrix Matrix::operator!() // Òðàíñïîçèöèÿ

{ Matrix A(n,m);

for(int i=0, j; i

for(j=0; j

A(j,i)=(*this)(i,j);

return A;

}

template

VARTYPE Matrix::determ() // ðåêóðñèâíî íàõîäèò îïðåäåëèòåëü ìàòðèöû

{

if (n!=m) ERROR_MATRIX(4);

if (n==1)

return (*this)(0,0);

for(int i=0; i

if ((*this)(i,0))

{

static Matrix M;

M <<= *this;

VARTYPE d=M(i,0)*(i%2?-1:1);

return d*M.Gauss(i,0).minor(i,0).determ();

}

return 0.0;

}

template

VARTYPE Matrix::vmodul() // Ìîäóëü âåêòîðà

{

VARTYPE d=0;

if (n!=1) ERROR_MATRIX(9);

static Matrix M;

M <<= *this;

for(int i=0; i

d=d+M(i,0)*M(i,0);

return sqrt(d);

}

template

Matrix& Matrix::Gauss(dim M, dim N)

{

Matrix& A=*this;

if (!A(M,N)) ERROR_MATRIX(5);

for(int i=0,j;i

for(j=0;j

if (i!=M && j!=N)

A(i,j)-=A(M,j)*A(i,N)/A(M,N);

for(j=0;j

if (j!=N)

A(M,j)/=A(M,N);

for(i=0;i

A(i,N)=0;

A(M,N)=1;

return *this;

}

template

Matrix Matrix::minor(dim M, dim N)// âîçâðàù. ìàòðèöó áåç

{// ñòðîêè y è ñòîëáöà x

Matrix A(m-1,n-1);

for(int i=0,in=0,j,jn;i

if (i!=M)

{

for(j=0,jn=0;j

if (j!=N)

A(in,jn++)=(*this)(i,j);

in++;

}

return A;

}

template // âñòàâêà

Matrix& Matrix::insert(const Matrix &A, dim M, dim N)

{

if (M+A.m>m || N+A.n>n) ERROR_MATRIX(6);

for(int i=0, j; i

for(j=0; j

(*this)(i+M,j+N)=A(i,j);

return *this;

}

template // èçâëå÷åíèå

Matrix Matrix::extract(dim LM, dim LN, dim M, dim N)

{

if (M+LM>m || N+LN>n) ERROR_MATRIX(7);

Matrix A(LM,LN);

for(int i=0, j; i

for(j=0; j

A(i,j)=(*this)(i+M,j+N);

return A;

}

template

VARTYPE& Matrix::operator() (dim M, dim N) const

{ return *(matr+n*M+N); }

template

Matrix operator+(const Matrix &A, const Matrix&B)

{

Matrix C=A;

for(int i=0,j; i

for(j=0; j

C(i,j)+=B(i,j);

return C;

}

template

Matrix operator-(const Matrix &A, const Matrix &B)

{

Matrix C=A;

for(int i=0, j; i

for(j=0;j

C(i,j)-=B(i,j);

return C;

}

template

Matrix operator*(const Matrix &A,const Matrix &B)

{

Matrix C(A.m,B.n);

if (A.n!=B.m)

{

if(A.m==3 && A.n==1 && B.m==3 && B.n==1)

{

C(0)=A(1)*B(2)-A(2)*B(1);

C(1)=A(2)*B(0)-A(0)*B(2);

C(2)=A(0)*B(1)-A(1)*B(0);

}

else

A.ERROR_MATRIX(2);

}

else

{

for(int i=0,j,k;i

for(j=0;j

for(k=0;k

C(i,j)+=A(i,k)*B(k,j);

}

return C;

}

template //óìíîæåíèå ÷èñëà íà ìàòðèöó

Matrix operator*(const double &f,const Matrix &A)

{

Matrix B=A;

for(int i=0,j;i

for(j=0;j

B(i,j)*=f;

return B;

}

template // óìíîæåíèå ìàòðèöû íà ÷èñëî

Matrix operator*(const Matrix &A, const double &f)

{

Matrix B=A;

for(int i=0,j;i

for(j=0;j

B(i,j)*=f;

return B;

}

template

Matrix& Matrix::newsize(dim M, dim N)

{ delete [] matr;

m=M;

n=N;

if (N && M) { matr=new VARTYPE[m*n];

if (!matr) ERROR_MATRIX(1);

setmem(matr,sizeof(VARTYPE)*m*n,0); }

else { m=n=0; matr=(VARTYPE*)0; }

return *this;

}

template

ostream& operator<<(ostream &out,Matrix &A)

{ for(int i=0,j;i

{ for(j=0;j

out << A(i,j)<< " ";

out<

}

return out;

}

template

int operator>>(istream &inp,Matrix &A)

{ for(int i=0,j;i

for(j=0;j>A(i,j)) ) return 1;

return 0;

}

template

void Matrix::swap_line(dim L1, dim L2)

{

if (L1==L2)

return;

double b;

for(int j=0;j

{

b=(*this)(L1,j);

(*this)(L1,j)=(*this)(L2,j);

(*this)(L2,j)=b;

}

}

template

void Matrix::swap_column(dim C1, dim C2)

{

if (C1==C2)

return;

double b;

for(int i=0;i

{

b=(*this)(i,C1);

(*this)(i,C1)=(*this)(i,C2);

(*this)(i,C2)=b;

}

}

template

dim Matrix::read(ifstream &finp)

{ (finp.get(m)).get(n); delete []matr; matr=new VARTYPE[m*n];

if(!matr) ERROR_MATRIX(1);

setmem(matr,sizeof(VARTYPE)*m*n,0);

finp.read((char *)matr,sizeof(VARTYPE)*m*n); return finp.fail();

}

template

dim Matrix::write(ofstream &fout)

{ (fout.put(m)).put(n);

(fout.write((char *)matr,sizeof(VARTYPE)*m*n))<

}

template

VARTYPE operator%(const Matrix &A, const Matrix&B)

{

if(A.n!=1 || B.n!=1) A.ERROR_MATRIX(9);

if(A.m!=B.m) A.ERROR_MATRIX(0);

VARTYPE scalarmul = 0;

for(int i=0; i

scalarmul = scalarmul+A(i)*B(i);

return scalarmul;

}

template

void Matrix::ERROR_MATRIX(dim E) const

{ static char *message[] = {

"Ìàòðèöû äîëæíû èìåòü îäèíàêîâóþ ðàçìåðíîñòü",//0

"Íå âûäåëåíà ïàìÿòü!",//1

"Ìàòðèöû íå ñîãëàñîâàíû äëÿ óìíîæåíèÿ",//2

"Ñòåïåíü äîëæíà áûòü áîëüøå íóëÿ èëè -1",//3

"Ìàòðèöà äîëæíà áûòü êâàäðàòíîé",//4

"Íóëåâîé âåäóùèé ýëåìåíò â ïðåîáðàçîâàíèè Ãàóññà",//5

"Âñòàâêà íåâîçìîæíà èç-çà ïåðåêðûòèÿ áàçîâîé ìàòðèöû",//6

"Èçâëåêàåìàÿ ìàòðèöà âûõîäèò çà ãðàíèöû áàçîâîé",//7

"Âûõîä çà ãðàíèöû. Ïîïûòêà äîñòóïà ê íåñóù. ýëåìåíòó",//8

"Ýòî íå âåêòîð!"};//9

cerr<<"ERROR: "<< message[E] << endl; exit(1);

}

Äåìîíñòðàòèâíî - òåñòèðóþùàÿ ïðîãðàììà:

#include

#include

#include

#include "tmatr.cpp"

int main()

{

clrscr();

Matrix A(3,3), B(3,3), C(3,3);

Matrix V(3),X(3),H(3),U(3);

double d;

A(0,0)=1.1; A(0,1)=2.2; A(0,2)=3.3;

A(1,0)=2.4; A(1,1)=1.1; A(1,2)=4.4;

A(2,0)=1.3; A(2,1)=2.1; A(2,2)=4.1;

B(0,0)=2; B(0,1)=7; B(0,2)=2;

B(1,0)=4; B(1,1)=8; B(1,2)=1;

B(2,0)=6; B(2,1)=4; B(2,2)=1;

V(0)=2.1; V(1)=3.31; V(2)=1.4;

H(0)=1.1; H(1)=2.1; H(2)=3.1;

//******************************

C=A+B;

cout<<"A:n"<

cout<<"B:n"<

cout<<"C=A+B:n"<

cout<<"Press any key...n";

getch();

clrscr();

//******************************

C=A-B;

cout<<"A:n"<

cout<<"B:n"<

cout<<"C=A-B:n"<

cout<<"Press any key...n";

getch();

clrscr();

//******************************

//******************************

X=V+H;

cout<<"V:n"<

cout<<"H:n"<

cout<<"X=V+H:n"<

cout<<"Press any key...n";

getch();

clrscr();

//******************************

X=V-H;

cout<<"V:n"<

cout<<"H:n"<

cout<<"X=V-H:n"<

cout<<"Press any key...n";

getch();

clrscr();

 

C=A*V;

cout<<"A:n"<

cout<<"V:n"<

cout<<"C=A*V:n"<

cout<<"Press any key...n";

getch();

clrscr();

//******************************

Matrix D(3,3), E(3,3);

D(0,0)=1; D(0,1)=2; D(0,2)=3;

D(1,0)=2; D(1,1)=5; D(1,2)=6;

D(2,0)=7; D(2,1)=3; D(2,2)=9;

ofstream fout("test.mtr");

if(!fout)

{

cout<<"file not openn";

return 1;

}

D.write(fout);

fout.close();

ifstream fin("test.mtr");

if(!fin)

{

cout<<"file not openn";

return 1;

}

E.read(fin); //

cout<<"D:n";

cout<

cout<<"E:n";

cout<

fin.close();

cout<<"Press any key...n";

getch();

clrscr();

//************************************

C=A^-1;

cout<<"A:n"<

cout<<"C=A^-1:n"<

cout<<"Press any key...n";

getch();

clrscr();

//****************************

// A*X=V X=(A^-1)*V

 

X=(A^-1)*V;

cout<<"A^-1:n"<<(A^-1)<

cout<<"V:n"<

cout<<"X:n"<

cout<<"Press any key...n";

getch();

clrscr();

//************************************

d=A.determ();

cout<<"determinant of A = "<

d=V.vmodul();

cout<<"modul of V = "<

cout<<"Press any key...n";

getch();

clrscr();

//************************************

V(0)=4; V(1)=3; V(2)=2;

U(0)=1; U(1)=2; U(2)=3;

d=V%U;

cout<<"scalar product V*U= "<< d<

cout<<"Press any key...n";

getch();

clrscr();

 

 

//************************************

C=!A;

cout<<"A:n"<

cout<<"C=!A:n"<

cout<<"Press any key...n";

getch();

clrscr();

C=5*A;

B=A*2;

cout<<"A:n"<

cout<<"C=5*A:n"<

cout<<"B=A*2:n"<

cout<<"Press any key...n";

getch();

clrscr();

//************************************

//************************************

return 0;

 

 

Ðåçóëüòàòû òåñòèðîâàíèÿ êëàññà Matrix

Ñëîæåíèå ìàòðèö A è B:

A:B:C=A+B:

1.12.23.32723.19.25.3

2.41.14.44816.49.15.4

1.32.14.16417.36.15.1

Âû÷èòàíèå ìàòðèö A è B:

A:B:C=A-B:

1.12.23.3272-0.9-4.81.3

2.41.14.4481-1.6-6.93.4

1.32.14.1641-4.7-1.93.1

Ñëîæåíèå ìàòðèö A è B:

A:B:C=A*B:

1.12.23.327230.838.57.7

2.41.14.448135.643.210.3

1.32.14.164135.642.38.8

Ñëîæåíèå âåêòîðîâ

V:

2.1

3.31

1.4

H:

1.1

2.1

3.1

X=V+H

3.2

5.41

4.5

Âû÷èòàíèå âåêòîðîâ

V:

2.1

3.31

1.4

 

 

H:

1.1

2.1

3.1

X=V-H:

1

1.21

-1.7

Óìíîæåíèå ìàòðèöû íà âåêòîð

A:

1.1 2.2 3.3

2.4 1.1 4.4

1.3 2.1 4.1

V:

2.1

3.31

1.4

C=A*V:

14.212

14.841

15.421

Çàïèñü ìàòðèöû â ôàéë

D:

1 2 3

2 5 6

7 3 9

Ñ÷èòûâàíèå ìàòðèöû èç ôàéëà

E:

1 2 3

2 5 6

7 3 9

 

 

Âû÷èñëåíèå îáðàòíîé ìàòðèöû

A:

1.1 2.2 3.3

2.4 1.1 4.4

1.3 2.1 4.1

 

C=A^-1:

2.009346 0.88785 -2.570093

1.750212 -0.093458 -1.308411

-1.53356 -0.233645 1.728972

Ðåøåíèå àëãåáðàè÷åñêîãî óðàâíåíèÿ

A^-1:

2.009346 0.88785 -2.570093

1.750212 -0.093458 -1.308411

-1.53356 -0.233645 1.728972

V:

2.1

3.31

1.4

X:

3.56028

1.534325

-1.57328

Îïðåäåëåíèå äåòåðìèíàíòà ìàòðèöû

determinant of A = -2.354

Îïðåäåëåíèå äëèíû (ìîäóëÿ) âåêòîðà

modul of V = 4.162463

Âû÷èñëåíèå ñêàëÿðíîãî ïðîèçâåäåíèÿ âåêòîðîâ

scalar product V*U= 16

ÂÛÂÎÄ

 ðåçóëüòàòå âûïîëíåíèÿ êóðñîâîãî ïðîåêòà áûëè ðàçðàáîòàíû äâà êëàññà ôóíêöèé äëÿ ðåøåíèÿ ïðîñòåéøèõ çàäà÷ ëèíåéíîé àëãåáðû. ×èñëî ýòèõ ôóíêöèé ñðàâíèòåëüíî íåâåëèêî, îäíàêî ìîæíî ëåãêî äîáàâèòü â ýòè êëàññû áîëåå ñëîæíûå ôóíêöèè, ïîñòðîåííûå íà áàçå óæå èìåþùèõñÿ. Êëàññû ïîçâîëÿþò ðàáîòàòü ñ ìàòðèöàìè è âåêòîðàìè, ýëåìåíòû êîòîðûõ ìîãóò áûòü ëþáîãî òèïà, îäíàêî íà ïðàêòèêå ÷àùå âñåãî èñïîëüçóåòñÿ öåëûé òèï è òèï ÷èñåë ñ ïëàâàþùåé çàïÿòîé.

Êëàññû íàïèñàíû íà ÿçûêå Ñ++, îäíàêî ìîãóò áûòü ëåãêî ïåðåïèñàíû íà ëþáîì èç ñîâðåìåííûõ ÿçûêîâ ïðîãðàììèðîâàíèÿ, òàê êàê ïðèâåäåíû äîâîëüíî ïðîñòûå àëãîðèòìû âñåõ êîìïîíåíòíûõ ôóíêöèé. Áûëè ìàêñèìàëüíî ïðåäóñìîòðåíû âñå âîçìîæíûå îøèáêè, êîòîðûå ìîãóò âîçíèêíóòü ïðè èñïîëüçîâàíèè ôóíêöèé äàííûõ êëàññîâ. Îñîáîå âíèìàíèå óäåëÿëîñü ðàçóìíîìó âûäåëåíèþ ïàìÿòè ïîä îáúåêòû âî âðåìÿ âûïîëíåíèÿ ïðîãðàììû, ïîýòîìó âñå ôóíêöèè áûëè òùàòåëüíî îòëàæåíû.

Êëàññû Matrix è Vector ìîãóò áûòü ýôôåêòèâíî ïðèìåíåíû íà ïðàêòèêå â çàäà÷àõ, òðåáóþùèõ îïåðàöèé ñ ìàòðèöàìè è âåêòîðàìè, à òàêæå ñâÿçàííûõ ñ ðåøåíèåì ñèñòåì ëèíåéíûõ àëãåáðàè÷åñêèõ óðàâíåíèé.

Ñïèñîê èñïîëüçîâàííîé ëèòåðàòóðû

Äèñêðåòíàÿ ìàòåìàòèêà, êîíñïåêò ëåêöèé. Â. Ã. Çàñîâåíêî. Çàïîðîæüå, 1998 ã.

Íà÷àëüíûé êóðñ Ñ è Ñ++. Á. È. Áåðåçèí. Ìîñêâà: "ÄÈÀËÎÃ-ÌÈÔÈ", 1999 ã.

ßçûê ïðîãðàììèðîâàíèÿ Ñ++. Á. Ñòðàóñòðóï. Êèåâ:"ÄèàÑîôò", 1993 ã.