Разработка средства функционального диагностирования вычислительных устройств
В данной курсовой работе выполняется проектирование блоков устройства контроля по модулю три матричного умножителя с сокращением вычислений для обработки мантисс чисел с плавающей точкой. Арифметическая операция выполняется с сохранением одинаковой разрядности для операндов и результатов. Операции с плавающей точкой содержат умножение, удваивающее разрядность полного результата. Поэтому при обработке мантисс по n-разрядным операндам вычисляется округленный n-разрядный результат, т.е. Имеет место потеря n младших разрядов полного 2n-разрядного результата.
Использование сокращенных методов выполнения операций позволяет вдвое или почти вдвое снизить затраты оборудования и времени на выполнение операции.
Методы функционального диагностирования обеспечивают достоверность функционирования вычислительных устройств. Основным методом функционального диагностирования вычислительных устройств является контроль по модулю. Он обладает высокой обнаруживающей способностью и простотой реализации для полноразрядных вычислительных устройств. Функциональное диагностирование современных вычислительных устройств требует умения выполнять контроль по модулю производительных вычислительных устройств с плавающей точкой. Поэтому в курсовой работе затрагивается этот вопрос.
1. Определение варианта задания
Вариант задания определяется по номеру Z = 104, который был выдан преподавателем. Курсовая работа является комплексной – номер варианта выдается двум студентам. Я выполняю первую часть работы – разрабатываю блоки контроля вычисления контрольных кодов КА и КВ.
По номеру Z определяются параметры:
X = Z mod 9 = 10 mod 9 = 1,
Y = Z mod 4 = 10 mod 4 = 2.
По параметру X определяется шаг изменения размеров образующих фрагмента:
X mod 3 = 5 mod 3 = 2 – остаток и 1 – частное, т.е. шаг для верхнего фрагмента равен 2, а для нижнего фрагмента – 4.
Параметр Y определяет сомножители, по которым образующие верхних и нижних фрагментов меняют свой размер. Для Y равного 2, верхнее и нижнее разбиения задаются по операнду В.
Вариант задается видом разбиения матрицы конъюнкций прозведения на фрагменты (МКП).
2. Разбиение МКП на фрагменты
Разбиение МКП на фрагменты представлено на рис. 1.
Фрагменты разбиения:
V1 = – A{6}*B{36}*2-42
V2 = – A {7,8}*B {35,36}*2-44
V3 = – A{8}*B{34}*2-42
V4 = – A {9:12}*B {33:36}*2-48
V5 = – A{10}*B{32}*2-42
V6 = – A {11,12}*B {31,32}*2-44
V7 = – A{12}*B{30}*2-42
V8 = – A {13:16}*B {29:36}*2-52
V9 = – A{14}*B{28}*2-42
V10 = – A {15,16}*B {27,28}*2-44
V11 = – A{16}*B{26}*2-42
V12 = – A {17:20}*B {25:36}*2-56
V13 = – A{18}*B{24}*2-42
V14 = – A {19,20}*B {23,24}*2-44
V15 = – A{20}*B{22}*2-42
V16 = – A {21:36}*B {21:36}*2-72
V17 = – A{22}*B{20}*2-42
V18 = – A {23,24}*B {19,20}*2-44
V19 = – A{24}*B{18}*2-42
V20 = – A {25,26}*B {17:20}*2-46
V21 = – A{26}*B{16}*2-42
V22 = – A {27,28}*B {15:20}*2-48
V23 = – A{28}*B{14}*2-42
V24 = – A {29,30}*B {13:20}*2-50
V25 = – A{30}*B{12}*2-42
V26 = – A {31,32}*B {11:20}*2-52
V27 = – A{32}*B{10}*2-42
V28 = – A {33,34}*B {9:20}*2-54
V29 = – A{34}*B{8}*2-42
V30 = – A {35,36}*B {7:20}*2-56
V31 = – A{36}*B{6}*2-42
V32 = – A {1:36}*B {1:36}*2-72
3. Формирование контрольных кодов КАi и КВi
Составляемые контрольные коды (их длина не превышает L = 2, так как M = 3):
1) KA1 = A{6}*2-6 = A{6}
KA2 = A {7,8}*2-8 = A {7,8}
KA3 = A{8}
KA5 = A{10}
KA6 = A {11,12}
KA7 = A{12}
KA9 = A{14}
KA10 = A {15,16}
KA11 = A{16}
KA13 = A{18}
KA14 = A {19,20}
KA15 = A{20}
KA17 = A{22}
KA18 = A {23,24}
KA19 = A{24}
КА20 = A {25,26}
KA21 = A{26}
KA22 = A {27,28}
KA23 = A{28}
КА24 = A {29,30}
KA25 = A{30}
KA26 = A {31,32}
KA27 = A{32}
КА28 = A {33,34}
KA29 = A{34}
KA30 = A {35,36}
KA31 = A{36}
2) KB1 = B{36}*2-36 = B{36}
KB2 = B {35,36}*2-36 = B {35,36}
KB3 = B{34}
KB5 = B{32}
KB6 = B {31,32}
KB7 = B{30}
KB9 = B{28}
KB10 = B {27,28}
KB11 = B{26}
KB13 = B{24}
KB14 = B {23,24}
KB15 = B{22}
KB17 = B{20}
KB18 = B {19,20}
KB19 = B{18}
KB21 = B{16}
KB23 = B{14}
KB25 = B{12}
KB27 = B{10}
KB29 = B{8}
KB31 = B{6}
Вычисляемые контрольные коды (формируются при длине частей операндов превышающей L):
KA4 = (KA6 + A{9}*2-9 + A{10}*2-10) mod 3 = (KA6 – A{9} +A{10}) mod 3
KA8 = (KA10 – A{13} + A{14}) mod 3
KA12 = (KA14 – A{17} + A{18}) mod 3
KA16 = (KA18 + KA20 + KA22 + KA24 + KA26 + KA28 + KA30 – A{21} + A{22}) mod 3
KA32 = (KA16 + KA12 + KA8 + KA4 – A {1,3,5,7} + A {2,4,6,8}) mod 3
KB4 = (B{34}*2-34 +B{33}*2-33 + KB2) mod 3 = (KB2 + B{34} – B{33}) mod 3
KB8 = (B{30} – B{29} + KB4 + KB6) mod 3
KB12 = (B{26} – B{25} + KB8 + KB10) mod 3
KB16 = (B{22} – B{21} + KB12 + KB14) mod 3
KB20 = (B{18} – B{17} + KB18) mod 3
KB22 = (B{16} – B{15} + KB20) mod 3
KB24 = (B{14} – B{13} + KB22) mod 3
KB26 = (B{12} – B{11} + KB24) mod 3
KB28 = (B{10} – B{9} + KB26) mod 3
KB30 = (B{8} – B{7} + KB28) mod 3
KB32 = (B {2,4,6} – B {1,3,5} + KB30 + KB16) mod 3
Блоки контроля операндов
На сумматорах по модулю три выполняется свертка операндов А и В с формированием вычисляемых контрольных кодов КАi и КBi. Последние вычисляемые контрольные коды КА32 и КB32 являются результатами свертки. Они сравниваются на сумматоре по модулю три с входными контрольными кодами КА операнда А и КВ операнда В соответственно. Для этого входной контрольный код подключен инверсно: первый разряд – к входу с весом 2, а второй разряд – к входу с весом 1. На первом прямом и инверсном втором выходах сумматора по модулю три формируется код контроля ККА операнда А (ККВ операнда В).
Блок контроля вычисления контрольных кодов КAi
Для рассматриваемого разбиения МКП блок контроля БКА с прямым порядком вычисления контрольных кодов КAi представлен в приложении 1.
Блок контроля вычисления контрольных кодов КBi
Для рассматриваемого разбиения МКП блок контроля БКБ с прямым порядком вычисления контрольных кодов КВi представлен в приложении 2.
Описание блоков устройства контроля
Схемы блоков устройства контроля описываются прямым списком, который оформляется с использованием таблиц.
Для каждого элемента заполняется отдельная таблица. Столбец таблицы содержит описание соединений входов и выходов одного элемента. Входами элемента являются входы устройства контроля или выходы других элементов.
Описание схемы блока контроля БКА приведено в табл. 1.
Таблица 1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Вх1
1
5
9
13
17
21
25
29
33
118
122
126
128
132
136
Вх2
2
6
10
14
18
22
26
30
34
119
123
127
129
133
137
Вх1
3
7
11
15
19
23
27
31
35
120
124
0
130
134
138
Вх2
4
8
12
16
20
24
28
32
36
121
125
0
131
135
139
Вых1
118
120
122
124
126
128
130
132
134
136
138
140
142
144
146
Вых2
119
121
123
125
127
129
131
133
135
137
139
141
143
145
147
Таблица 1 продолжение
16
17
18
19
20
21
Вх1
140
142
146
150
152
38
Вх2
141
143
147
151
153
37
Вх1
0
144
148
0
154
157
Вх2
0
145
149
0
155
158
Вых1
148
150
152
153
156
159
Вых2
149
151
153
154
157
160
Описание схемы блока контроля БКБ приведено в табл. 2.
Таблица 2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Вх1
39
43
55
59
63
67
71
161
165
171
177
169
177
167
185
Вх2
40
44
56
60
64
68
72
162
166
172
178
170
178
168
186
Вх1
41
0
57
61
65
69
73
163
53
173
51
179
49
183
47
Вх2
42
0
58
62
66
70
74
164
54
174
52
180
50
184
48
Вых1
161
163
165
167
169
171
173
175
177
179
181
183
185
187
189
Вых2
162
164
166
168
170
172
174
176
178
180
182
184
186
188
190
Таблица 2 продолжение
16
17
18
19
Вх1
175
189
191
76
Вх2
176
190
192
75
Вх1
187
45
193
195
Вх2
188
46
197
196
Вых1
191
193
195
197
Вых2
192
194
196
198
6. Алгоритмы получения описаний
Процедуры получения описаний схем блоков устройства контроля формализованы в виде алгоритмов составления таблиц.
Таблицы представляются двухмерными массивами данных.
Для разработки алгоритмов были выполнены:
Обобщение содержания таблиц, с помощью выделения среди ее чисел ключевых данных и выражения их через параметры n, k;
Определение закономерностей изменения чисел в столбцах и строках таблицы.
Алгоритм, описывающий табл. 1., представлен в приложении 3.
Блок 2 описывает ввод данных:
n – разрядность МКП;
k – количество отбрасываемых разрядов.
В блоке 3,4 и 5 представлены ключевые данные:
d1 = первое значение в таблице 1, которое соответствует разрядности МКП;
d2 = 4*n – k + 5 – номер выхода первого сумматора по модулю три в схеме.
d3 = n/2+3 – количество столбцов в таблице 1.
L = n – k – Количество разрядов в усеченном результате.
as1 = (n/4 +n % 2) – Количество сумматоров в первом ряду.
as2 = as1 + L – Количество сумматоров во втором ряду.
as3 = (as2+as2% 2) /2 – Количество сумматоров в третьем ряду.
as4 = (as3+as3% 2) /2 – Количество сумматоров в четвертом ряду.
Блоки 10,6 определяет данные последнего столбца элементоа первого ряда табл. 1.
В блоках 7 – 9 задан цикл по столбцам, начиная со второго и заканчивая последним столбцом. В цикле определяют данные последних двух строк таблицы. Номер выхода в строке увеличивается на 2 для каждого последующего столбца.
В блоках 11 – 15 заданы циклы по строкам 1: 4 и по столбцам 1: as1. В цикле определяются входы сумматоров по модулю три, определяющих вычисляемые контрольные коды.
Блок 16,17 определяет данные первого столбца элементоа первого ряда табл. 1.
Блок 18,19,23 – подпрограмма заполняющая массив х. В подпрограмму передаем следующие параметры imin, imax, iinc, jmin, jmax, jinc,
В блоке 20–22, задаются номера входов разрядов контрольного кода КА16 {1,2}, а также номер выхода первого в таблице сумматора по модулю три, который подается на вход следующего сумматора.
В блоке 27–29, задаются номера входов разрядов контрольного кода КА12 {1,2}, а также номер выхода первого в таблице сумматора по модулю три, который подается на вход следующего сумматора.
В блоке 24–26, заполним столбцы таблицы, первый столбец в четвертом ряду
В блоке 30, задаются номера входов разрядов контрольного кода КА32 {1,2}, а также номер выхода первого в таблице сумматора по модулю три, который подается на вход следующего сумматора.
Блок 31 вычитаем из свернутого операнда А его ККА, получаем признак корректности результата.
В блоке 32 производится вывод данных.
Алгоритм, описывающий табл. 2., представлен в приложении 3.
Блок 2 описывает ввод данных:
n – разрядность МКП;
k – количество отбрасываемых разрядов.
В блоке 3 представлены ключевые данные:
d1 = (n-k)* 2 – первое значение в таблице 1;
d2 = 8*n – 5*k -3 – номер выхода первого сумматора в таблице. 2.
d3 = n – k – 3 – количество столбцов в таблице 2.
as1 = n/4–2 – Количество сумматоров в первом ряду.
Tail, head – переменые(указатели) хранят номер опорного и «заполняемого» элемента
Блоки 56,62 определяют данные первого столбца таблицы 2.
В блоках 63 – 65 задан цикл по столбцам, начиная со второго и заканчивая последним столбцом. В цикле определяют данные последних двух строк таблицы, а также первых двух строк. Номер выхода в строке увеличивается на 2 для каждого последующего столбца.
В блоках 57 – 61 заданы циклы по строкам 1: 4 и по столбцам 1: as1. В цикле определяются входы сумматоров по модулю три, определяющих вычисляемые контрольные коды.
В блоках 66 – 68 заполняются первый два столбца таблицы.
Заполнением данными столбцы 9,11,13,15,17; 10,12,14,16.
Установим указатели tail и head, на опорный элемент, тот элемент откуда берутся данные, и тот, который заполняется.
В блоках 72 – 76 заполним данными 10,12,14,16 элементы. Инициализируем tail, head, затем вызываем подпрограмму, увеличиваем tail, head. В цикле определяются входы сумматоров по модулю три, определяющих вычисляемые контрольные коды. Определим КВ22, КВ24, КВ26, КВ28, КВ30.
В блоках 77 – 85 заполним 11,13,15,17 данными элементы. В цикле вызываем подпрограмму, увеличиваем tail, head. Определим КВ4, КВ8, КВ12, КВ16.
В блоке 86–88, задаются номера входов разрядов контрольного кода КВ32 {1,2}, а также номер выхода первого в таблице сумматора по модулю три, который подается на вход следующего сумматора.
Блок 89–91 вычитаем из свернутого операнда А его ККА, получаем признак корректности результата
В блоке 92 производится вывод данных.
7. Листинг программы, реализующей алгоритмы
Текст программы, реализующей описание схемы блока контроля БКА.БКв
void __fastcall TForm1: Button1Click (TObject *Sender)
{
int d3b, d3a;
n = StrToInt (Edit1->Text);
k = StrToInt (Edit2->Text);
d3a = n/2 + 3;
d3b = (n – n % 2)/2;
StringGrid1->ColCount = d3a;
StringGrid2->ColCount = d3b;
for (int i=1; i
StringGrid1->Cells[i] [0]=i;
for (int i=1; i
StringGrid2->Cells[i] [0]=i;
String stroca1 [7]={«», «Âõ1», «Âõ2», «Âõ3», «Âõ4», «Âûõ1», «Âûõ2»};
for (int i=0; i<=7; i++)
{
StringGrid1->Cells[0] [i]=stroca1 [i].c_str();
StringGrid2->Cells[0] [i]=stroca1 [i].c_str();
}
StrGr1 ();
StrGr2 ();
}
// –
void __fastcall TForm1: Cycle (TStringGrid *tab, int imin, int imax, int iinc, int jmin, int jmax, int jinc)
{
for (int i=imin; i
for (int j = jmin; j
if (n % 2 == 1) {
tab->Cells[i] [1] = tab->Cells [j-1] [6];
tab->Cells[i] [2] = tab->Cells [j-1] [5];
tab->Cells[i] [3] = tab->Cells[j] [6];
tab->Cells[i] [4] = tab->Cells[j] [5];
}
else {
tab->Cells[i] [1] = tab->Cells [j-1] [5];
tab->Cells[i] [2] = tab->Cells [j-1] [6];
tab->Cells[i] [3] = tab->Cells[j] [5];
tab->Cells[i] [4] = tab->Cells[j] [6];
}
}}}
// –
void __fastcall TForm1:IF1 (TStringGrid *tab, int head, int tail, int m)
{
if (n % 2 == 1) {
StringGrid1->Cells[head] [1] = StringGrid1->Cells[tail] [5];
StringGrid1->Cells[head] [2] = StringGrid1->Cells[tail] [6];
StringGrid1->Cells[head] [3] = StringGrid1->Cells[m] [5];
StringGrid1->Cells[head] [4] = StringGrid1->Cells[m] [6];
}
else
{
StringGrid1->Cells[head] [1] = StringGrid1->Cells[tail] [6];
StringGrid1->Cells[head] [2] = StringGrid1->Cells[tail] [5];
StringGrid1->Cells[head] [3] = StringGrid1->Cells[m] [6];
StringGrid1->Cells[head] [4] = StringGrid1->Cells[m] [5];
}}
// –
void __fastcall TForm1:IF2 (TStringGrid *tab, int head, int tail, int m, int m1)
{
if (n % 2 == 1) {
StringGrid1->Cells[head] [1] = StringGrid1->Cells[tail] [5];
StringGrid1->Cells[head] [2] = StringGrid1->Cells[tail] [6];
StringGrid1->Cells[head] [3] = StringGrid1->Cells[m] [5];
StringGrid1->Cells[head] [4] = StringGrid1->Cells[m] [6];
}
else
{
StringGrid1->Cells[head] [1] = StringGrid1->Cells[tail] [6];
StringGrid1->Cells[head] [2] = StringGrid1->Cells[tail] [5];
StringGrid1->Cells[head] [3] = m;
StringGrid1->Cells[head] [4] = m1;
}}
// –
void __fastcall TForm1: StrGr1 ()
{
int L, as1, as2, as3, as4, as5, d2a;
as1 = n/4 + n % 2;
as2 = as1 + L;
as3 = as2/2 + as2% 2;
as4 = as3/2 + as3% 2;
d2a = 4*n-k +5;
L = n-k;
StringGrid1->Cells[1] [5] = d2a;
StringGrid1->Cells[1] [6] = d2a+1;
for (int i=2; i
StringGrid1->Cells[i] [5] = StringGrid1->Cells [i-1] [5]+2;
StringGrid1->Cells[i] [6] = StringGrid1->Cells[i] [6]+2;
}
StringGrid1->Cells[as1] [1] = n – 3;
StringGrid1->Cells[as1] [2] = n – 2;
StringGrid1->Cells[as1] [3] = n – 1;
StringGrid1->Cells[as1] [4] = n;
for (int i=(as1–1); i>=0; i–)
for (int j=4; j<=0; j–)
StringGrid1->Cells[i] [j] = StringGrid1->Cells [i+1] [j] – 4;
if (n % 2 == 1) {
StringGrid1->Cells[1] [1] = 0;
StringGrid1->Cells[1] [2] = 0;
StringGrid1->Cells[1] [3] = 0;
StringGrid1->Cells[1] [4] = 1;
}
Cycle (StringGrid1, as2, (as2-L/2), – 1, as1,0, – 2);
Cycle (StringGrid1, as3, (as3-L/4), – 1, as2,0, – 2);
Cycle (StringGrid1, (as1+1), (as2-L/2–1), 1,0,4,2);
IF1 (StringGrid1, as3+1, as2+1, as2+2);
IF1 (StringGrid1, as5, as3+1, as3+2);
IF2 (StringGrid1, as5+1, as5, n+2, n+1);
}
// –
void __fastcall TForm1: StrGr2 ()
{
int d2b, d1, d3, bs1, tail, head, m, m1;
d2b = 8*n-5*k-3;
d1 = (n-k)*2;
d3 = n-k-3;
bs1= n/4–2;
StringGrid2->Cells[1] [5] = d2b;
StringGrid2->Cells[1] [6] = d2b+1;
for (int i=2; i
StringGrid2->Cells[i] [5] = StringGrid2->Cells [i-1] [5]+2;
StringGrid2->Cells[i] [6] = StringGrid2->Cells[i] [6]+2;
}
StringGrid2->Cells[bs1] [1] = n – 3;
StringGrid2->Cells[bs1] [2] = n – 2;
StringGrid2->Cells[bs1] [3] = n – 1;
StringGrid2->Cells[bs1] [4] = n;
for (int i=(bs1–1); i>d2b; i–)
for (int j=0; j<4; j++)
StringGrid2->Cells[i] [j] = StringGrid2->Cells [i+1] [j] – 4;
IF1 (StringGrid2, d1+2, d1, d3–2);
tail+=2;
head+=2;
IF1 (StringGrid2, d1+2, d1, d3–2);
if (n % 2 == 1) {
StringGrid2->Cells [head+2] [1] = StringGrid2->Cells[head] [6];
StringGrid2->Cells [head+2] [2] = StringGrid2->Cells[head] [5];
StringGrid2->Cells [head+2] [3] = StringGrid2->Cells [d3+1] [6];
StringGrid2->Cells [head+2] [4] = StringGrid2->Cells [d3+1] [5];
}
tail= d3;
m= 4*(k-1);
head = bs1+2;
for (int i=1; i
{
IF2 (StringGrid2, head, tail, m, m-1);
tail+=2;
head+=2;
}
IF1 (StringGrid2, head, d1, d1+1);
IF1 (StringGrid2, head, tail, n/4–2);
IF2 (StringGrid2, head, tail, 2*n+4,2*n+3);
}
Результаты работы программы
В программе была задана разрядность n = 36 и количество отбрасываемых разрядов k = 31. Разбиение МКП представлено на рис. 2.
Блоки контроля БКА и БКБ представлены в приложении 4.
Описание схемы блока контроля БКА приведено в табл. 4.
Таблица 4
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Вх1
1
5
9
13
17
21
25
29
33
118
122
126
128
132
136
Вх2
2
6
10
14
18
22
26
30
34
119
123
127
129
133
137
Вх1
3
7
11
15
19
23
27
31
35
120
124
0
130
134
138
Вх2
4
8
12
16
20
24
28
32
36
121
125
0
131
135
139
Вых1
118
120
122
124
126
128
130
132
134
136
138
140
142
144
146
Вых2
119
121
123
125
127
129
131
133
135
137
139
141
143
145
147
Таблица 4 продолжение
16
17
18
19
20
21
Вх1
140
142
146
150
152
38
Вх2
141
143
147
151
153
37
Вх1
0
144
148
0
154
157
Вх2
0
145
149
0
155
158
Вых1
148
150
152
153
156
159
Вых2
149
151
153
154
157
160
Описание схемы блока контроля БКБ приведено в табл. 5.
Таблица 5
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Вх1
39
43
55
59
63
67
71
161
165
171
177
169
177
167
185
Вх2
40
44
56
60
64
68
72
162
166
172
178
170
178
168
186
Вх1
41
0
57
61
65
69
73
163
53
173
51
179
49
183
47
Вх2
42
0
58
62
66
70
74
164
54
174
52
180
50
184
48
Вых1
161
163
165
167
169
171
173
175
177
179
181
183
185
187
189
Вых2
162
164
166
168
170
172
174
176
178
180
182
184
186
188
190
Таблица 5 продолжение
16
17
18
19
Вх1
175
189
191
76
Вх2
176
190
192
75
Вх1
187
45
193
195
Вх2
188
46
197
196
Вых1
191
193
195
197
Вых2
192
194
196
198
Список литературы
Рабинович З.Л., Раманаускас В.А. Типовые операции в вычислительных машинах. – Киев: Техника, 1980.
Савельев А.Я. Прикладная теория цифровых автоматов. – М.: Высш. шк. 1987.

Нравится материал? Поддержи автора!
Ещё документы из категории информатика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ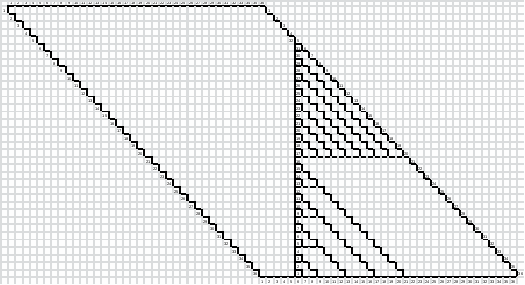 Введение
Введение