Симплекс метод решения задачи линейного программирования
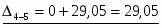
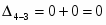
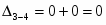
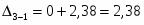
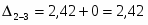
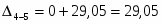
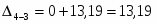
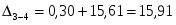
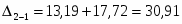
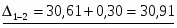
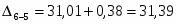
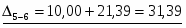
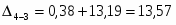
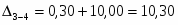
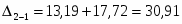
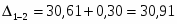
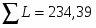
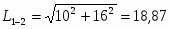
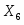
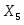
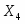
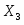
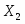
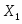
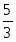
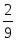
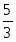
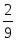
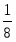
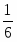
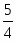
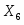
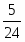
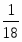
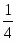
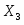
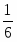
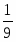
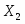
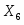
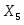
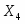
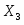
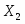
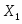
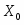
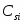
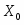
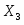
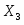
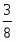
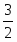
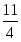
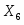
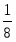
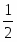
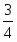
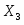
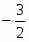
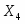
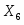
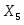
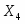
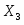
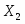
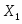
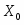
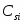
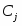
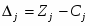
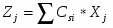
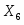
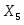
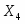
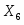
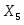
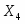
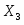
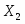
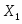
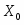
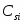
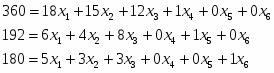
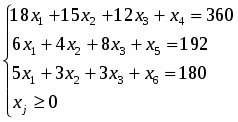
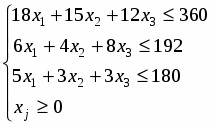Задача №1 (Симплекс метод решения задачи линейного программирования.)
Найти F max = 9x1+ 10x2 + 16x3, при ограничениях:
Запишем задачу в каноническом виде:
F=9x1+ 10x2 + 16x3 → max
Заполним начальную таблицу:
Таблица 0.
0
9
10
16
0
0
0
Отношение,
θ
i
Базис
1
0
360
18
15
12
1
0
0
30
2
0
192
6
4
8
0
1
0
24
3
0
180
5
3
3
0
0
1
60
∆j
0
-9
-10
-16
0
0
0
Zj
0
0
0
0
0
0
0
Zj вычисляется по формуле
Оценки (∆j) вычисляются по формуле , где - коэффициент из первой строки таблицы.
Выбираем минимальную (отрицательную) оценку. Она определяет направляющий столбец.
Заполняем столбец «θ», по минимальному значению определяем направляющую строку.
На пересечение строки и столбца находится направляющий элемент.
Заполняем новую таблицу
Таблица 1.
0
9
10
16
0
0
0
Отношение,
θ
i
Базис
1
0
72
9
9
0
1
0
8
2
16
24
1
0
0
48
3
0
108
0
0
-
1
72
∆j
384
3
-2
0
0
2
0
Zj
384
12
8
0
0
2
0
Изменяется базис в позиции направляющей строки. Базисным становится вектор, соответствующий направляющему столбцу, т. е.
Столбец становится базисным, то есть единичным.
Новые значения в направляющей строке получаем делением элементов этой строки на направляющий элемент.
Остальные элементы в небазисных столбцах и в столбце вычисляем по правилу треугольника.
Выбираем минимальную отрицательную оценку. Она определяет направляющий столбец.
Заполняем столбец «θ»
По минимальному значению определяем направляющую строку.
На пересечении направляющей строки и столбца находится направляющий элемент.
Заполнение второй таблицы осуществляется по аналогии с предыдущей.
Таблица 2.
0
9
10
16
0
0
0
Отношение,
θ
i
Базис
1
10
8
1
1
0
-
0
______
2
16
20
0
1
-
0
______
3
0
96
0
0
-
1
______
∆j
400
5
0
0
0
Zj
400
14
10
16
0
Так как нет отрицательных оценок ∆j, значит выполняется признак оптимальности и не вводились искусственные переменные, то получено оптимальное решение.
Ответ:
Максимальное значение функции F max =400 достигается в точке с координатами:
=0
=8
=20
=0
=0
=96
Задача №2 (Метод Литтла)
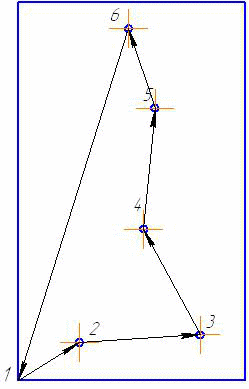
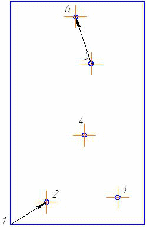
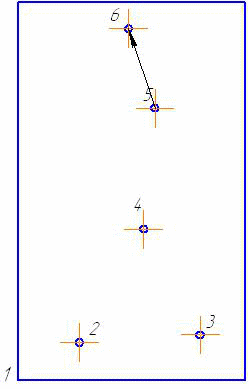
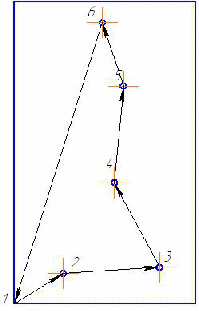
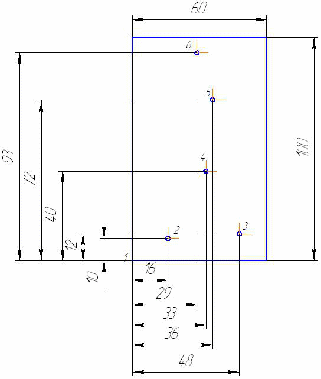
Найти кратчайший путь в графе, заданном графически в виде чертежа, методом Литтла.
Из чертежа запишем матрицу расстояний. (Расстояние от т.1 до т.2 равно:
, и т.д.)
1
2
3
4
5
6
1
∞
18,87
49,48
51,86
80,51
97,42
2
18,87
∞
32,06
34,48
65,15
84,01
3
49,48
32,06
∞
31,76
61,19
83,20
4
51,86
34,48
31,76
∞
32,14
53,15
5
80,51
65,15
61,19
32,14
∞
22,14
6
97,42
84,01
83,20
53,15
22,14
∞
Предположим что кратчайший путь будет следующим:
т.1→ т.2→ т.3→ т.4→ т.5→ т.6→т.1 и составит
Решение: Первый этап.
Шаг 1. Приведем матрицу расстояний по строкам и столбцам
(в строке вычитаем из каждого элемента минимальный, затем в столбцах)
1
2
3
4
5
6
1
∞
18,87
49,48
51,86
80,51
97,42
18,87
2
18,87
∞
32,06
34,48
65,15
84,01
18,87
3
49,48
32,06
∞
31,76
61,19
83,20
31,76
4
51,86
34,48
31,76
∞
32,14
53,15
31,76
5
80,51
65,15
61,19
32,14
∞
22,14
22,14
6
97,42
84,01
83,20
53,15
22,14
∞
22,14
↓
1
2
3
4
5
6
1
∞
0
30,61
32,99
61,64
78,55
2
0
∞
13,19
15,61
46,28
65,14
3
17,72
0,30
∞
0
29,43
51,44
4
20,10
2,72
0
∞
0,38
21,39
5
58,37
43,01
39,05
10,00
∞
0
6
75,28
61,87
61,06
31,01
0
∞
0
0
0
0
0
0
↓
1
2
3
4
5
6
1
∞
0
30,61
32,99
61,64
78,55
2
0
∞
13,19
15,61
46,28
65,14
3
17,72
0,30
∞
0
29,43
51,44
4
20,10
2,72
0
∞
0,38
21,39
5
58,37
43,01
39,05
10,00
∞
0
6
75,28
61,87
61,06
31,01
0
∞
Шаг 2. Определим оценки нулевых клеток:
Шаг 3. Вычеркиваем клетку с максимальной оценкой. Включаем данную клетку в путь обхода. (5 – 6)
Шаг 4. Переписываем матрицу расстояний, накладывая запрет на одну из клеток для исключения преждевременного замыкания контура (в клетку 6-5 ставим ∞).
1
2
3
4
5
1
∞
0
30,61
32,99
61,64
2
0
∞
13,19
15,61
46,28
3
17,72
0,30
∞
0
29,43
4
20,10
2,72
0
∞
0,38
6
75,28
61,87
61,06
31,01
∞
Далее повторяем шаги 1 – 4, пока не дойдем до одной клетки.
Второй этап.
Шаг 1. Приведем матрицу расстояний по строкам и столбцам.
1
2
3
4
5
1
∞
0
30,61
32,99
61,64
2
0
∞
13,19
15,61
46,28
3
17,72
0,30
∞
0
29,43
4
20,10
2,72
0
∞
0,38
6
75,28
61,87
61,06
31,01
∞
0
0
0
0
0,38
↓
1
2
3
4
5
1
∞
0
30,61
32,99
61,26
2
0
∞
13,19
15,61
45,90
3
17,72
0,30
∞
0
29,05
4
20,10
2,72
0
∞
0
6
75,28
61,87
61,06
31,01
∞
Шаг 2. Определим оценки нулевых клеток:
Шаг 3. Вычеркиваем клетку с максимальной оценкой. Включаем данную клетку в путь обхода. (1 – 2)
Шаг 4. Переписываем матрицу расстояний, накладывая запрет на одну из клеток для исключения преждевременного замыкания контура (в клетку 2 – 1 ставим ∞).
1
3
4
5
2
∞
13,19
15,61
45,90
3
17,72
∞
0
29,05
4
20,10
0
∞
0
6
75,28
61,06
31,01
∞
Третий этап.
Шаг 1. Приведем матрицу расстояний по строкам и столбцам.
1
3
4
5
2
∞
13,19
15,61
45,90
3
17,72
∞
0
29,05
4
20,10
0
∞
0
6
75,28
61,06
31,01
∞
17,72
0
0
0
↓
1
3
4
5
2
∞
13,19
15,61
45,90
13,19
3
0
∞
0
29,05
0
4
2,38
0
∞
0
0
6
57,56
61,06
31,01
∞
31,01
↓
1
3
4
5
2
∞
0
2,42
32,71
3
0
∞
0
29,05
4
2,38
0
∞
0
6
26,55
30,05
0
∞
Шаг 2. Определим оценки нулевых клеток:
Шаг 3. Вычеркиваем клетку с максимальной оценкой. Включаем данную клетку в путь обхода. (4 – 5)
Шаг 4. Переписываем матрицу расстояний, накладывая запрет на одну из клеток для исключения преждевременного замыкания контура (в клетку 6 – 4 ставим ∞).
1
3
4
2
∞
0
2,42
3
0
∞
0
6
26,55
30,05
∞
Четвертый этап.
Шаг 1. Приведем матрицу расстояний по строкам и столбцам.
1
3
4
2
∞
0
2,42
0
3
0
∞
0
0
6
26,55
30,05
∞
26,55
↓
1
3
4
2
∞
0
2,42
3
0
∞
0
6
0
3,50
∞
Шаг 2. Определим оценки нулевых клеток:
Шаг 3. Вычеркиваем клетку с максимальной оценкой. Включаем данную клетку в путь обхода. (3 – 4)
Шаг 4. Переписываем матрицу расстояний, накладывая запрет на одну из клеток для исключения преждевременного замыкания контура (в клетку 6 – 3 ставим ∞).
1
3
2
∞
0
6
0
∞
Пятый этап.
Остались не задействованными связи 2 – 3 и 6 – 1.
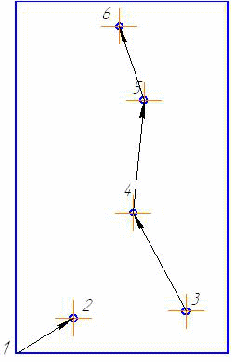
В результате получаем следующую цепочку:
1→ 2→ 3 → 4→ 5→ 6 →1
Длина пути составляет:
L=18,87+32,06+31,76+32,14+22,14+97,42=234,39
это и есть кратчайший путь.
Нравится материал? Поддержи автора!
Ещё документы из категории информатика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ