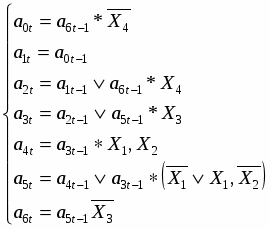
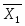
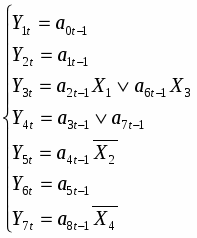
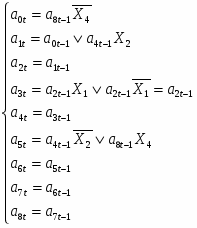
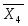
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

НАЦІОНАЛЬНІЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ „ХПІ"

Кафедра „Обчислювальна техніка та програмування”

Синтез мікропрограмних автоматів

Альбом документів курсового проекту по дисципліні

"Спеціалізовані комп’ютерні системи"

КІТ32.02198.022 ДКП

Керівник проекту:

___________

Виконав:

студент групи

____________________

„ __” ___________________ 2007 р.

Харків

Зміст

Вступ

1. Технічне завдання

1.1 Синтезувати мікропрограмний автомат за схемою Уілкса-Стрінжера у вигляді автомата Мілі

1.2 Синтезувати мікропрограмний автомат за схемою Уілкса-Стрінжера у вигляді автомата Мура

2. Базові теоретичні дані

2.1 Основні дані про автомати

2.2 Класифікація атоматів

3. Методика вирішення

3.1 Синтез мікропрограмного автомата за схемою Уілкса-Стрінжера у вигляді автомата Мілі

3.1.1 Змістовна схема алгоритму

3.1.2 Змістовна таблиця кодування операційних та умовних верхівок

3.1.3 Закодована мікроопераційна схема алгоритму

3.1.4 Таблиця кодування мікрокоманд

3.1.5 Закодована мікрокомандна схема алгоритма

3.1.6 Основна таблиця автомата (СІ - синхроімпульс)

3.1.7 Граф-схема переходів

3.1.8 Система рівнянь переходів

3.1 9. Система рівнянь виходів

3.1.10 Кодування внутрішніх станів автомата

3.1.11 Побудова схеми операційного автомата

3.1.12 Схема операційного автомата

3.2 Синтез мікропрограмного автомата за схемою Уілкса-Стрінжера у вигляді автомата Мура

3.2.1 Змістовна схема алгоритму

3.2.2 Змістовна таблиця кодування операційних та умовних верхівок

3.2.3 Закодована мікроопераційна схема алгоритма

3.2.4 Таблиця кодування мікрокоманд

3.2.5 Закодована мікрокомандна схема алгоритма

3.2.6 Основна таблиця автомата (СІ - синхроимпульс)

3.2.7 Граф-схема переходів

3.2.8 Система рівнянь переходів

3.2.9 Кодування внутрішніх станів автомата

3.2.10 Побудова схеми операційного автомата

3.2.11 Схема операційного автомата

Висновки

Список літератури

Вступ

Поряд з теорією формальних мов і заснованих на ній методів побудови компіляторів кінцеві автомати активно використовуються в комп'ютерних іграх, у реалізації мережних протоколів, системах стиску інформації. Іншими словами, там, де потрібна велика надійність і де логіка поводження надто складна, щоб програміст зміг реалізувати її на одному лише рівні здорового глузду.

З появою структурного програмування стало очевидним, що з трьох головних конструкторів керування: проходження, циклу і розгалуження останній є найважчим у сприйнятті програміста, оскільки при безлічі альтернатив перетворює лінеаризовану структуру алгоритму в деревоподібну. При цьому складність навіть послідовних програм росте стрімко і часом може перевершувати дерево варіантів у настільки непростий для автоматичного аналізу моделі, як традиційні шахи. Розбивка програми на процеси й об'єкти з заміною багатоступінчастого розгалуження засобами обробки повідомлень (подій) заміняє одну проблему на іншу: вкладеність зменшується, зате кількість взаємодіючих компонентів помітно зростає. Логіка "розмивається" і в підсумку ми одержуємо погано контрольовану ситуацію, коли через хаотичність "ручного" синтезу і неможливості побудувати вичерпний набір тестів немає ніякої впевненості в коректності побудованої системи. Ключ до рішення складається в застосуванні формальних методів, у створенні зручної абстракції, здатної "вичавити" з алгоритму квінтесенцію логіки його роботи і дати можливість проводити весь необхідний аналіз. Однією з таких зручних абстракцій можуть служити кінцеві автомати, серед різновидів яких варто виділити автомати Мілі і Мура. Близькість до булевої алгебри і теорії графів, наочність графічного представлення і детермінованість поводження є помітними достоїнствами цієї абстракції.

1. Технічне завдання

1.1 Синтезувати мікропрограмний автомат за схемою Уілкса-Стрінжера у вигляді автомата Мілі

Побудувати операційний автомат, що обчислює кількість парних елементів у двох одномірних масивах (A [n], B [m]).

Мікропроцесорний автомат необхідно реалізувати за схемою Уілкса-Стрінжера у вигляді автомата Мілі.

Оптимальну функціональну схему керуючих частин автомата синтезувати на елементах системи І, АБО, НЕ, RS-, D - тригерах, доповнюючи її необхідними по алгоритму функціональними автоматами.

1.2 Синтезувати мікропрограмний автомат за схемою Уілкса-Стрінжера у вигляді автомата Мура

Побудувати операційний автомат, який знаходить максимальний парний елемент в кожному рядку масива (A [n,n]).

Мікропрограмний автомат необхідно реалізувати за схемою Уілкса-Стрінжера у вигляді автомата Мура.

Оптимальну функціональну схему керуючих частин автомата синтезувати на елементах І, НЕ, RS-, D - тригерах.

2. Базові теоретичні дані

2.1 Основні дані про автомати

Автомат - модель пристрою з кінцевою пам'яттю, призначена для обробки інформації.

В абстрактному змісті автомат - зовсім не чорний ящик, що переробляє послідовність вхідних дискретних сигналів у послідовність вихідних сигналів. У загальному випадку, автомат представляється схемою, основними частинами якої є логічний перетворювач і пам’ять. Логічний перетворювач складається з логічних елементів, з'єднаних один з одним у необхідну схему. У правильно спроектованому автоматі логічні елементи і весь логічний перетворювач можуть вважатися безінерційними, притаманні елементам запізнювання в зміні сигналів використовуються для створення пам’яті. В автоматі виділяються чотири види сигналів: вхідні, вихідні, проміжні і синхронізуючі. Якщо число вхідних і вихідних сигналів кінцеве, то схема представляє кінцевий автомат.

Кінцевий автомат - це схема, що має обмежений набір станів. Роль кінцевих автоматів складається в тому, що будь-яка система (наприклад, програма), що володіє обмеженим набором можливостей, що можуть бути позначені окремими станами (чи навіть їх комбінаціями), може бути представлена кінцевим автоматом. Кінцеві автомати природні для програми керування (операційних систем) на комп'ютері та для трансляторів. Кінцевий автомат є моделлю, яка широко використовується при створенні різних пристроїв обробки інформації.

2.2 Класифікація атоматів

Розрізняють два класи кінцевих автоматів. Синхронний автомат характеризується тим, що генератор тактових імпульсів синхронізації впливає через вхід S на автомат, поділяючи час на такти. Інтервали часу між тактовими імпульсами повинні бути більше будь-якої затримки. Вихідні сигнали в синхронному автоматі зчитуються тільки під час видачі цих імпульсів, коли під впливом вхідних і проміжних сигналів автомат перейшов вже в новий стан. В асинхронному автоматі вихідні сигнали зчитуються в будь-який час, а перехід у новий стан визначається лише часом спрацьовування всіх логічних елементів, що входять у логічний перетворювач. На вхід S не подається ніякий сигнал (цей вхід відсутній).

Пристрої, які створені на основі асинхронного автомата, характеризуються високою швидкодією. Однак, синхронні автомати розробляються в більш короткий термін, легко налагоджуються і модифікуються. Синхронні автомати легко стикуються з комп'ютерами, що також є синхронними пристроями.

Кінцеві автомати створюються на базі Інтегральних Схем (ІС). Особливо зручна їх реалізація на основі програмувальних логічних матриць (ПЛМ). Часто логічний перетворювач виконується у виді однієї інтегральної схеми.

3. Методика вирішення

3.1 Синтез мікропрограмного автомата за схемою Уілкса-Стрінжера у вигляді автомата Мілі

Побудувати операційний автомат, що обчислює кількість парних елементів у двох одномірних масивах (A [n], B [m]).

Мікропроцесорний автомат необхідно реалізувати за схемою Уілкса-Стрінжера у вигляді автомата Мілі.

Оптимальну функціональну схему керуючих частин автомата синтезувати на елементах системи І, АБО, НЕ, RS-, D - тригерах, доповнюючи її необхідними по алгоритму функціональними автоматами.

3.1.1 Змістовна схема алгоритму

До складу змістовної схеми алгоритму (Рис.1) входять операційні та умовні верхівки. Наш алгоритм виконує знаходження кількості парних елементів у двох одномірних масивах розмірністю [n] та [m], використовуючи при цьому чотири (4) умовні верхівки і десять (10) операційних верхівок. Позначення операційних верхівок показано на Рис.2. Позначення умовних верхівок на Рис.3. Перевірка елементів масивів виконується від стовпчика до стовпчика.

Рис.1.

ПОЧАТОК

i = 1

kol = 0

A[i]

A[i] mod 2 = 0

max

kol = kol + 1

i  n

кінець

i = i + 1

так

так

i = 1

B[i]

B[i] mod 2 = 0

max

kol = kol + 1

i  m

i = i + 1

так

так

kol

Рис.3.

Рис.2.

3.1.2 Змістовна таблиця кодування операційних та умовних верхівок

Кожна верхівка, чи то операційна чи умовна, кодується. При чому, якщо, мікро операції повторюються і умовні верхівки повторюються, вони кодуються однаково. У даному прикладі мікрооперації повторюються двічі, тому, однакові верхівки ми можемо кодувати одним кодом. Таблиця кодування верхівок зображена у Таблиці1.

Таблиця1

Код

Зміст

Примітка

mY₁

i = 1

mY₂

kol = 0

mY₃

A [i]

Ввід А [і]

mY₄

kol = kol + 1

mY₅

i = i + 1

mY₆

B [i]

mY₇

kol

Вивід kol

X₁

A [i] mod 2 = 0

так - 1, ні - 0

X₂

i  n

так - 1, ні - 0

X₃

B [i] mod 2 = 0

так - 1, ні - 0

X₄

i ≤ m

так - 1, ні - 0

3.1.3 Закодована мікроопераційна схема алгоритму

Закодована мікроопераційна схема алгоритму будується на основі змістовної схеми алгоритму (Рис.1) і таблиці кодування операційних та умовних верхівок (Таблиця 1), шляхом заміни відповідних блоків. Схема алгоритму зображена на Рис.4.

Рис. 4.

початок

mY₁

mY₂

mY₃

X₁

mY₄

X₂

кінець

mY₅

1

1

mY₁

mY₆

X₃

mY₄

X₄

mY₅

1

1

mY₇

0

0

0

0

3.1.4 Таблиця кодування мікрокоманд

Складаємо таблицю кодування мікрокоманд. Кожна мікрооперація кодується своєю мікрокомандою. Мікрооперації, які виконуються одна за одною послідовно на протязі одного такту часу, поєднуються до однієї мікрокоманди. У даному прикладі дві мікрооперації (mY₁, mY₂) виконуються одна за одною послідовно. Тому ми поєднуємо їх в одну мікрокоманду. Таблиця кодування зображена в Таблиці 2.

Таблиця 2

Мікрокоманда

Мікрооперація

Y₁

mY₁, mY₂

Y₂

mY₃

Y₃

mY₄

Y₄

mY₅

Y₅

mY₁

Y₆

mY₆

Y₇

mY₇

3.1.5 Закодована мікрокомандна схема алгоритма

Складаємо закодовану мікрокомандну схему алгоритму (Рис.5). Проставляємо мітки внутрішніх станів автомата Мілі таким чином:

мітки ставляться після кожної мікрокоманди (перед блоком після операційного);

початок та кінець мікрокомандної схеми алгоритму відмічається міткою а₀;

мітки проставляються згідно з порядковим номером;

* a_0Х

Y₆

Y_1х

X₁

Y₃

X₂

Y₄

1

1

Y₅

X₃

Y₃

X₄

Y₄

1

1

0

0

0

0

Y₂

Y₇

* a₀

* a₈

* a₇

* a₆

* a₅

* a₄

* a₃

* a₂

* a₁

Рис.5.

3.1.6 Основна таблиця автомата (СІ - синхроімпульс)

Будуємо основну таблицю автомата (Таблиця 3). Ця таблиця складається на основі закодованої мікрокомандної схеми алгоритму (Рис.5) В першому стовпчику таблиці записуються усі стани, в яких може знаходитися наш автомат. В першому рядку таблиці записуються способи переходу автомата з одного стану в інший (вхідні сигнали), тобто, чи то буде СІ (той перехід, в процесі якого на шляху не зустрілась жодна верхівка), чи то при переході автомату буде поставлена умова. В клітинках таблиці фіксується, перехід до якого стану здійснюється, і що буде на виході. Наприклад, із стану а₀ автомат може здійснити перехід до стану а₁ і в результаті цього переходу на виході автомата буде Y₁, тобто, автомат виконає ті мікрооперації, які виконуються на протязі одного такту часу (mY₁ і mY₂ закодовані мікрокомандою Y₁), при чому, цей перехід станеться під синхроімпульсним сигналом.

Таблиця 3

СІ=1

X₁

X₂

X₃

X₄

a₀

a₁/Y₁

a₁

a₂/Y₂

a₂

a₃/Y₃

a₃/__

a₃

a₄/Y₄

a₄

a₁/__

a₅/Y₅

a₅

a₆/Y₆

a₆

a₇/Y₃

a₇/__

a₇

a₈/Y₄

a₈

a₅/__

a₀/Y₇

3.1.7 Граф-схема переходів

Будуємо граф-схему переходів (Рис.7). Граф-схема будується на основі Рис.5. і Таблиці 3. Кружочками позначаються можливі стани автомата. Стрілки указують на перехід із стану i до стану j. Над стрілкою указується, під яким вхідним сигналом станеться перехід, і, що при цьому буде на виході автомата.

a₁

a₃

a₂

a₄

a₇

a₈

a₀

a₅

a₆

Рис. 7.

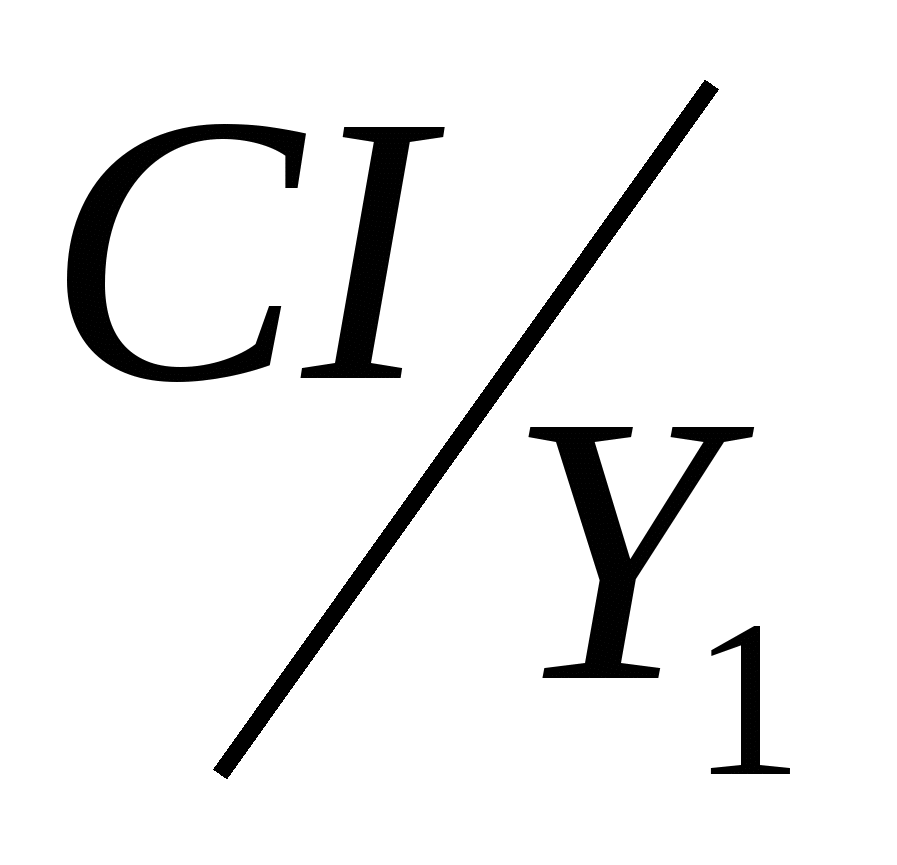
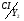
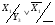
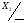
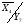
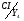
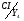
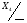
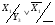
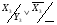
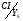
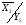
3.1.8 Система рівнянь переходів

Складаємо систему рівнянь переходів. Ця система складається на основі граф-схеми переходів (Рис.7) або основної таблиці абстрактного автомата (Таблиця 3). Сигнал СІ опущений.

3.1 9. Система рівнянь виходів

Складаємо систему рівнянь виходів. Ця система складається на основі закодованої мікрокомандної схеми алгоритму (Рис.5), де Х - вхід,

Y - вихід.

3.1.10 Кодування внутрішніх станів автомата

Для того, щоб закодувати внутрішні стани автомата, визначаємо кількість необхідних для цього тригерів (n). Кількість тригерів розраховується із співвідношення: log₂ A ≤ n, де

n - кількість необхідних тригерів;

А - кількість станів а_i (a₀ - a₈)

А = 9log₂ 9 ≤ nn = 4,Нам необхідні 4 тригери, значить внутрішні стани автомата будемо кодувати чотирьох-розрядним двійковим кодом. Процес кодування зображений у Таблиці 4.

Таблиця 4

S₁

S₂

S₃

S₄

a₀

0

0

0

0

a₁

0

0

0

1

a₂

0

0

1

0

a₃

0

0

1

1

a₄

0

1

0

0

a₅

0

1

0

1

a₆

0

1

1

0

a₇

0

1

1

1

a₈

1

0

0

0

3.1.11 Побудова схеми операційного автомата

Операційний автомат складається з п’яти (5) частин (Рис.5).

У вхідній частині розташовані чотири (4) RS-тригери, чотири (4) логічних елементи АБО, на які подається вхідний сигнал, декодер та дві шини, одна з яких необхідна для передачі сигналів, які надходять з декодера, а інша - для сигналів з виходів компаратора.

У перехідній частині автомата виконується перетворення сигнала на протязі одного такту часу. Пройшовши через логічні елементи І та (або) АБО, чи того не роблячи, сигнал змінюється і результат надходить на шину (a_t), відкіля продовжує передаватися до програмованої логічної матриці (ПЛМ). Перехідна частина будується на основі системи рівнянь переходів.

Вихідна частина. Ця частина будується на основі системи рівнянь виходів. Тут виконується той самий процес, що й у перехідній частині, тільки сигнали подаються на вихідну шину Y_t, з якої сигнал надходить до вихідної матриці.

3.1.12 Схема операційного автомата

1

S T2

R

S T1

R

1

S T3

R

1

&

1

&

S T4

R

1

DC

X₁

X₂

X₃

X₄

&

1

&

1

2

3

4

5

6

7

8

1

2

3

4

1

2

3

4

0

1

2

3

4

5

6

7

8

8

0

4

1

2

3

4

8

50

6

8

3

4

7

7

0

1

2

3

4

5

6

7

8

0

1

2

3

4

5

7

6

1

2

3

4

5

6

7

8

S1

R1

S2

R2

S3

R3

S4

R4

8

&

1

&

1

&

&

7

7

7

7

0

1

1

1

1

1

2

2

2

2

3

3

3

3

4

4

4

4

4

5

5

5

5

5

6

6

6

6

8

8

8

mY₁

mY₂

mY₃

mY₄

mY₅

mY₆

mY₇

до процесора

виходи

компараторів

a_t-1 X_it

at

Пуск

вхідна частина

перехідна частина

програмована логічна

матриця

входи тригерів

вихідна частина

Рис. 8.

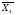
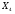
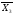
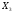
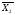
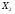
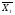
3.2 Синтез мікропрограмного автомата за схемою Уілкса-Стрінжера у вигляді автомата Мура

Побудувати операційний автомат, який знаходить максимальний парний елемент в кожному рядку масива (A [n,n]).

Мікропрограмний автомат необхідно реалізувати за схемою Уілкса-Стрінжера у вигляді автомата Мура.

Оптимальну функціональну схему керуючих частин автомата синтезувати на елементах І, НЕ, RS-, D - тригерах.

3.2.1 Змістовна схема алгоритму

До складу змістовної схеми алгоритму (Рис.1) входять операційні та умовні верхівки. Наш алгоритм виконує знаходження максимального парного елементу кожному рядку масива, використовуючи при цьому чотири (4) умовні верхівки і вісім (8) операційних верхівок. Позначення операційних верхівок показано на Рис.2. Позначення умовних верхівок на Рис.3.

Рис.2.

Рис.3.

Рис.1.

початок

j = 1

i = 1

max = 0

A[i,j]

A[i,j]%2

max = A[i,j]

max

i < n

кінець

j < n

i = i + 1

j = j + 1

так

так

так

A[i,j]>

max

так

3.2.2 Змістовна таблиця кодування операційних та умовних верхівок

Кожна верхівка, чи то операційна чи умовна, кодується. При чому, якщо, мікрооперації повторюються і умовні верхівки повторюються, вони кодуються однаково. В даному прикладі три мікрооперації повторюються двічі, тому, однакові верхівки ми можемо кодувати одним кодом. Таблиця кодування верхівок зображена у Таблиці1.

Таблиця 1

Код

Зміст

Примітки

mY1

j = 1

mY2

i = 1

mY3

max = 0

mY4

A [i,j]

Ввід A [i,j]

mY5

max = A [i,j]

mY6

i = i + 1

mY7

max

Вивід max

mY8

j = j + 1

X1

A [i,j]% 2

так - 1, ні - 0

X2

A [i,j] > max

так - 1, ні - 0

X3

i < n

так - 1, ні - 0

X4

j < m

так - 1, ні - 0

3.2.3 Закодована мікроопераційна схема алгоритма

Закодована мікроопераційна схема алгоритму будується на основі змістовної схеми алгоритму (Рис.1) і таблиці кодування операційних та умовних верхівок (Таблиця 1), шляхом заміни відповідних блоків. Схема алгоритму зображена на Рис.4.

Рис. 4.

початок

mY1

mY2

mY3

mY4

X1

mY5

mY7

X3

кінець

X4

mY6

mY8

1

1

1

X2

1

3.2.4 Таблиця кодування мікрокоманд

Складаємо таблицю кодування мікрокоманд. Кожна операція кодується своєю мікрокомандою. Мікрооперації, які виконуються одна за одною послідовно на протязі одного такта часу, об’єднуються в одну мікрокоманду. В даному прикладі двічі по дві мікрооперації ( (mY₂, mY₃) и (mY₇, mY₈)) виконуються послідовно. Тому ми об’єднуємо їх в одну мікрокоманду. Таблиця кодування зображена в Таблиці 2.

Таблиця 2

Мікрокоманда

Мікрооперація

Y1

mY1

Y2

mY2,mY3

Y3

mY4

Y4

mY5

Y5

mY6

Y6

mY7, mY8

3.2.5 Закодована мікрокомандна схема алгоритма

Складаємо закодовану мікрокомандну схему алгоритма (Рис.5). Проставляємо мітки внутрішніх станів автомата Мура таким чином:

мітки ставляться біля кожної мікрокоманди;

початок і кінець мікрокомандної схеми алгоритма відмічається міткою а₀;

перехід з одного стану в інший повинен проходити через умовну або операційну верхівки автомата;

- біля кожної мікрокоманди мітки проставляються відповідно порядковому номеру;

Рис.5.

a₀

a₀

a₆

a₅

a₄

a₃

a₂

a₁

Y1

Y3

Y2

X1

Y4

X3

X4

Y5

Y6

1

1

1

X2

1

3.2.6 Основна таблиця автомата (СІ - синхроимпульс)

Будуємо основну таблицю автомата Мура (Таблиця 3). Ця таблиця складається на основі закодованої мікрокомандної схеми алгоритму

(Рис.5) У першому стовпчику таблиці записуються стани, в яких може збути наш автомат. В першому рядку таблиці записуються способи переходу автомата з одного стану в інший (вхідні сигнали), тобто, чи то буде СІ (той перехід, в процесі якого на шляху не зустрілася жодна вершина), чи при переході автомату буде поставлена умова. В клітинках таблиці фіксується, перехід в який стан виконується та, що буде на виході. Наприклад, із стану а₀ автомат може здійснити перехід у стан а₁ і в результаті цього переходу на виході автомата буде Y₁, тобто, автомат виконає ті мікрооперації, які виконуються на протязі одного такту часу (mY₁ закодована мікрокомандою Y₁), при чому, цей перехід станеться під синхроімпульс ним сигналом.

Таблиця 3

СІ=1

X₁, X₂

X₁,

X₃

X₄

a₀

a₁/Y₁

a₁

a₂/Y₂

a₂

a₃/Y₃

a₃

a₅/Y₅

a₄/Y₄

a₅/Y₅

a₄

a₅/Y₅

a₅

a₃/Y₃

a₆/Y₆

a₆

a₂/Y₂

a₀/ __

3.2.7 Граф-схема переходів

Будуємо граф-схему переходів (Рис.7). Граф-схема будується на основі Рис.5. і Таблиці 3. Кружочками позначаються можливі стани автомата. Стрілки указують на перехід із стану i до стану j. Над стрілкою указується, під яким вхідним сигналом станеться перехід і, що при цьому буде на виході автомата.

Рис. 7.

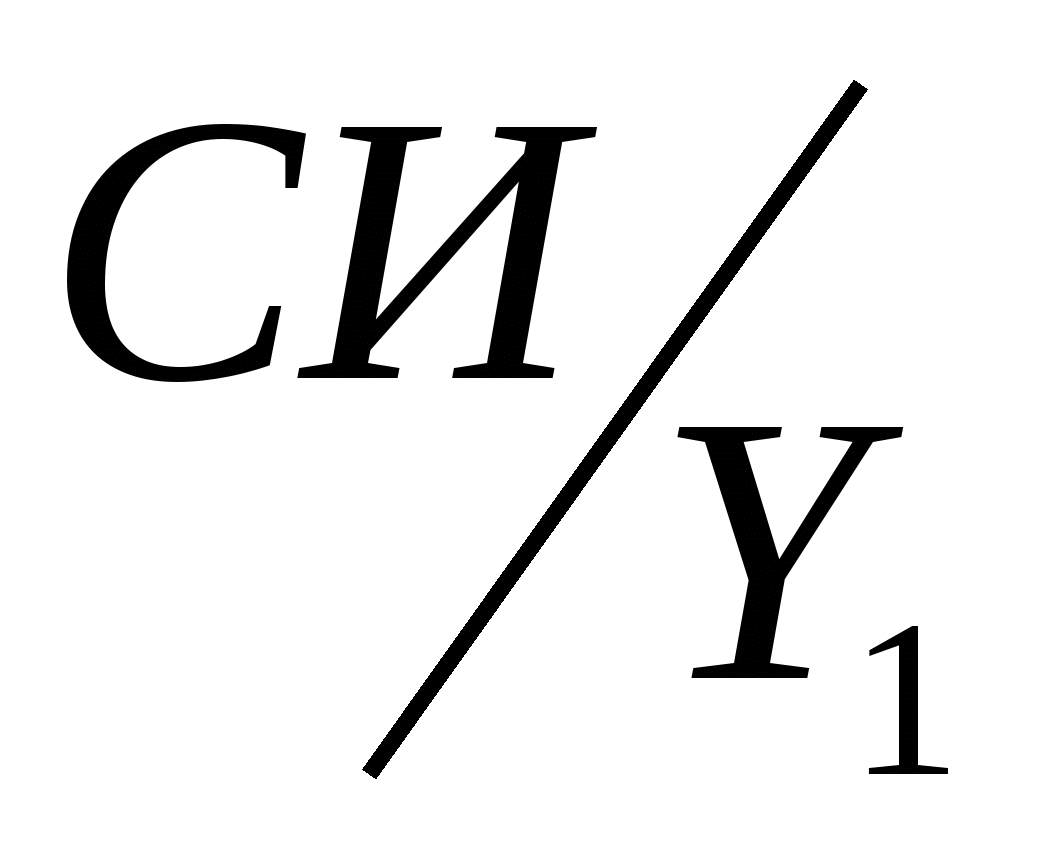
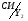
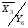
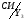
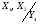
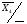
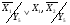
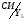
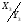
a₁

a₃

a₂

a₄

a₀

a₅

a₆

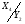
3.2.8 Система рівнянь переходів

Складаємо систему рівнянь переходів. Ця система складається на основі граф-схеми переходів (Рис.7) або основної таблиці абстрактного автомата (Таблиця 3).

3.2.9 Кодування внутрішніх станів автомата

Для того, щоб закодувати внутрішні стани автомата, визначаємо кількість необхідних для цього тригерів (n). Кількість тригерів розраховується із співвідношення: log₂ A ≤ n, де

n - кількість необхідних тригерів;

А - кількість міток а_i (a₀ - a₆)

А = 7log₂ 7 ≤ nn = 3,Оскільки, нам необхідно 3 тригера, то внутрішні стани автомата будемо кодувати трьох розрядним війковим кодом. Процес кодування зображений в Таблиці 4.

Таблиця 4

S₁

S₂

S₃

a₀

0

0

0

a₁

0

0

1

a₂

0

1

0

a₃

0

1

1

a₄

1

0

0

a₅

1

0

1

a₆

1

1

0

3.2.10 Побудова схеми операційного автомата

Операційний автомат складається з трьох (3) частин (Рис.5).

У вхідній частині розташовані три (3) D-тригери, три (3) логічних елементи АБО, на які подається вхідний сигнал, декодер та дві шини, одна з яких необхідна для передачі сигналів, які надходять з декодера, а інша - для сигналів з виходів компаратора.

У перехідній частині автомата виконується перетворення сигнала на протязі одного такту часу. Пройшовши через логічні елементи І та (або) АБО, чи того не роблячи, сигнал змінюється і результат надходить на шину (a_t), відкіля продовжує передаватися до програмованої логічної матриці. Перехідна частина будується на основі системи рівнянь переходів.

Вихідна частина. Ця частина будується на основі системи рівнянь виходів. Тут виконується той самий процес, що й у перехідній частині, тільки сигнали подаються на вихідну шину Y_t, з якої сигнал надходить до вихідної матриці.

3.2.11 Схема операційного автомата

виходи

компараторів

вхідна частина

перехідна частина

програмована логічна

матриця

входи тригерів

Рис. 8.

1

S T2

R

S T1

R

1

S T3

R

1

&

1

&

DC

X₁

X₂

X₃

1

2

3

4

5

6

1

2

3

1

2

3

0

1

2

3

4

5

6

5

6

5

3

1

50

1

5

4

0

1

2

3

4

3

8

0

1

2

3

4

5

6

1

2

3

4

5

6

S1

R1

S2

R2

S3

R3

&

0

1

1

6

1

7

2

2

2

3

3

3

4

4

4

5

6

5

6

6

6

mY₁

mY₂

mY₃

mY₄

mY₅

mY₆

mY₇

a_t-1 X_it

at

Пуск

1

&

mY₈

2

3

&

1

&

&

8

7

Висновки

В результаті виконання курсового проекту повністю виконане індивідуальне завдання. Синтезовано мікропрограмний автомат за схемою Уілкса-Стрінжера у вигляді автомата Мілі, та автомат за схемою Уілкса-Стрінжера у вигляді автомата Мура.

Сформульовано докладні алгоритми виводу автоматів, та отримано кінцеві структурні схеми на І, АБО, НЕ, RS, D - тригерах і граф схеми переходів автоматів.

Список літератури

1.Model Reduction and Coarse-Graining Approaches for Multiscale Phenomena, Springer, Complexity series, Berlin-Heidelberg-New York, 2006. XII+562 pp.

2.Арнольд В.И. Жёсткие и мягкие математические модели. - М.: МЦНМО, 2004.

3.Блехман И.И., Мышкис А.Д., Пановко Н.Г., Прикладная математика: Предмет, логика, особенности подходов. С примерами из механики: Учебное пособие. - 3-е изд., испр. и доп. - М.: УРСС, 2006. - 376 с.

4.Кучумов А.И. Электроника и схемотехника: учеб. пособие для студ. вузов / А.И. Кучумов. - 2-е изд., перераб. и доп. - М.: Гелиос АРВ, 2004. - 335 с.

5.Новиков Ю.В. Основы цифровой схемотехники: базовые элементы и схемы, методы проектирования / Ю.В. Новиков. - М.: Мир, 2001. - 379 с

6.Советов Б.Я., Яковлев С.А., Моделирование систем: Учеб. для вузов - 3-е изд., перераб. и доп. - М.: Высш. шк., 2001. - 343 с.

7.Угрюмов Е.П. Цифровая схемотехника: учеб. пособие для студ. / Е.П. Угрюмов. - СПб.: BHV, 2004. - 518 с.