КОНТРОЛЬНАЯ РАБОТА

По дисциплине: «Системы и методы искусственного интеллекта в экономике»

Задание 1

1. Выбираем массив финансовых показателей по которым будем оценивать финансовую устойчивость предприятия. Устанавливаем эталонные значения данных показателей в каждой группе риска в соответствие с предложенными диапазонами значений финансовых показателей:

x1

x2

x3

x4

Показатели

Эталоны

критическая зона

зона опасности

зона относительной стабильности

зона благо-получия

Коэф. абсолютной ликвидности

0,18

0,24

0,38

0,47

Коэф. оборачиваемости собст-венных средств

0,71

0,85

0,96

1,7

Коэф. обеспеченности денежных средств и расчетов

0,03

0,08

0,14

0,21

Рентабельность использования всего капитала

0,02

0,09

0,12

0,19

Рентабельность продаж

0,05

0,14

0,26

0,31

2. Задаем характеристики исследуемого предприятия. Веса показателям устанавливаются экспертами.

s

n

Показатели

Исследуемое предприятие

Вектор весов показателей (выбирается экспертами)

Коэф. абсолютной ликвидности

0,57

9

Коэф. оборачиваемости собст-венных средств

0.49

3

Коэф. обеспеченности денежных средств и расчетов

0,53

7

Рентабельность использования всего капитала

2,4

4

Рентабельность продаж

1,8

5

3. Рассчитываем разницу между составляющими векторов исследуемого предприятия и каждого эталонного образа:

(s-xi)

0,39

0,33

0,19

0,10

-0,22

-0,36

-0,47

-1,21

0,50

0,45

0,39

0,32

2,38

2,31

2,28

2,21

1,75

1,66

1,54

1,49

4. Рассчитываем квадрат разницы между составляющими векторов исследуемого предприятия и каждого эталонного образа:

(s-xi)^2

0,1521

0,1089

0,0361

0,0100

0,0484

0,1296

0,2209

1,4641

0,2500

0,2025

0,1521

0,1024

5,6644

5,3361

5,1984

4,8841

3,0625

2,7556

2,3716

2,2201

5. Таким образом, расстояния по Эвклиду (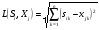) между исследуемым предприятием и эталонными образами будут равны:

х1

х2

х3

х4

Расстояния по Эвклиду

9,1774

8,5327

7,9791

8,6807

Минимальное расстояние между исследуемым предприятием и эталоном свидетельствует о принадлежности исследуемого предприятия к области риска х3 (зона относительной стабильности).

6. Рассчитываем разницу между составляющими векторов исследуемого предприятия и каждого эталонного образа, возведенную в степень λ=4:

(s-xi)^λ, λ=4

0,02313441

0,01185921

0,00130321

0,00010000

0,00234256

0,01679616

0,04879681

2,14358881

0,06250000

0,04100625

0,02313441

0,01048576

32,08542736

28,47396321

27,02336256

23,85443281

9,37890625

7,59333136

5,62448656

4,92884401

7. Таким образом, расстояния по Минковскому (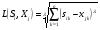) между исследуемым предприятием и эталонными образами будут равны:

х1

х2

х3

х4

Расстояние по Минковскому

41,55231058

36,13695619

32,72108355

30,93745139

Минимальное расстояние между исследуемым предприятием и эталоном свидетельствует о принадлежности исследуемого предприятия к области риска х4 (зона благополучия).

8. Рассчитываем модуль разницы между составляющими векторов исследуемого предприятия и каждого эталонного образа:

|s-xi|

0,39

0,33

0,19

0,10

0,22

0,36

0,47

1,21

0,50

0,45

0,39

0,32

2,38

2,31

2,28

2,21

1,75

1,66

1,54

1,49

9. Таким образом, расстояния по модулю разницы (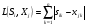) между исследуемым предприятием и эталонными образами будут равны:

х1

х2

х3

х4

Расстояние по модулю разности

5,24

5,11

4,87

5,33

Минимальное расстояние между исследуемым предприятием и эталоном свидетельствует о принадлежности исследуемого предприятия к области риска х3 (зона относительной стабильности).

10. Рассчитываем произведение весов коэффициентов и квадрата разницы между составляющими векторов исследуемого предприятия и каждого эталонного образа:

nj*(s-xi)^2

1,0647

0,7623

0,2527

0,0700

0,2904

0,7776

1,3254

8,7846

0,7500

0,6075

0,4563

0,3072

22,6576

21,3444

20,7936

19,5364

15,3125

13,7780

11,8580

11,1005

11. Таким образом, расстояния по Эвклиду с весами (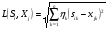) между исследуемым предприятием и эталонными образами будут равны:

х1

х2

х3

х4

Расстояние по Эвклиду (c весами)

40,0752

37,2698

34,6860

39,7987

Минимальное расстояние между исследуемым предприятием и эталоном свидетельствует о принадлежности исследуемого предприятия к области риска х3 (зона относительной стабильности).

12. Рассчитываем произведение весов коэффициентов и разницы между составляющими векторов исследуемого предприятия и каждого эталонного образа, возведенной в степень λ=4:

nj*(s-xi)^λ, λ=4

0,16194087

0,08301447

0,00912247

0,0007

0,01405536

0,10077696

0,29278086

12,86153286

0,1875

0,12301875

0,06940323

0,03145728

128,3417094

113,8958528

108,0934502

95,41773124

46,89453125

37,9666568

28,1224328

24,64422005

13. Таким образом, расстояния по Минковскому с весами (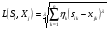) между исследуемым предприятием и эталонными образами будут равны:

х1

х2

х3

х4

Расстояние по Минковскому (c весами)

175,5997369

152,1693198

136,5871896

132,9556414

Минимальное расстояние между исследуемым предприятием и эталоном свидетельствует о принадлежности исследуемого предприятия к области риска х4 (зона благополучия).

14. Рассчитываем произведение весов коэффициентов и модулей разницы между составляющими векторов исследуемого предприятия и каждого эталонного образа:

nj*|s-xi|

2,73

2,31

1,33

0,7

1,32

0,4752

0,223344

0,27024624

1,5

1,35

1,17

0,96

9,52

9,24

9,12

8,84

8,75

8,3

7,7

7,45

15. Таким образом, расстояния по модулю разницы с весами (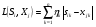) между исследуемым предприятием и эталонными образами будут равны:

х1

х2

х3

х4

Расстояние по модулю разности (c весами)

23,82

21,6752

19,543344

18,22024624

Минимальное расстояние между исследуемым предприятием и эталоном свидетельствует о принадлежности исследуемого предприятия к области риска х4 (зона благополучия).

16. Рассчитываем сумму между составляющими векторов исследуемого предприятия и каждого эталонного образа:

(s+xi)

0,75

0,24

0,77

0,80

1,20

0,85

0,74

1,34

0,56

0,08

0,64

0,66

2,42

0,09

2,50

2,50

1,85

0,14

2,01

1,97

17. Рассчитываем модуль отношения (s-x_i)/(s+x_i) для каждой составляющей векторов исследуемого предприятия и каждого эталонного образа:

|(s-xi)/(s+xi)|

0,52

1,375

0,246753

0,125

0,183333

0,423529

0,635135

0,902985

0,892857

5,625

0,609375

0,484848

0,983471

25,66667

0,912

0,884

0,945946

11,85714

0,766169

0,756345

18. Таким образом, расстояния по Камберру (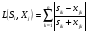) между исследуемым предприятием и эталонными образами будут равны:

х1

х2

х3

х4

Расстояние по Камберру

3,525607

44,94734

3,169433

3,153179

Минимальное расстояние между исследуемым предприятием и эталоном свидетельствует о принадлежности исследуемого предприятия к области риска х4 (зона благополучия).

ВЫВОД: В результате проведенного анализа можно сделать вывод о том, что уровень финансовой устойчивости исследуемого предприятия характеризуется относительной стабильностью и благополучием.

Задание 2

1. Задаем эталонные объекты, исследуемый образ и признаки, по которым будем оценивать сходство:

Вектор признаков

в него можно класть вещи

сделано преимущественно из одного материала

имеет дверцу

в него можно увидеть свое отражение

на нем сидят

окно

X₁

да

да

нет

да

нет

шкаф

X₂

да

да

да

нет

нет

стул

X₃

да

да

нет

нет

да

диван

X₄

да

нет

нет

нет

да

стол *

S

да

да

да

нет

нет

* Цветом выделен исследуемый образ.

2. Переводим качественные характеристики объектов в количественные. В результате формируется двоичный массив:

Вектор признаков

в него можно класть вещи

сделано преимущественно из одного материала

имеет дверцу

в него можно увидеть свое отражение

на нем сидят

окно

X₁

1

1

0

1

0

шкаф

X₂

1

1

1

0

0

стул

X₃

1

1

0

0

1

диван

X₄

1

0

0

0

1

стол *

S

1

1

1

0

0

3. Рассчитываем число совпадений наличия признаков объектов X_j, и S. Она может быть вычислена с помощью соотношения 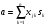(n – количество признаков). Для этого используем функцию СУММПРОИЗВ, указывая в ней массивы векторов значений признаков исследуемого образа и каждого из эталонного образов.

Таким образом:

A (количество совпадений присутствия признаков у исследуемого объекта и эталона X_j)

окно

X₁

2

шкаф

X₂

3

стул

X₃

2

диван

X₄

1

4. С помощью переменной b подсчитывается число случаев, когда объекты X_j, и S _. не обладают одним и тем же признаком, 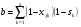. Для упрощения расчетов необходимо рассчитать матрицу значений (1-x_k) для всех исследуемых объектов:

(1-x_k)

окно

X₁

0

0

1

0

1

шкаф

X₂

0

0

0

1

1

стул

X₃

0

0

1

1

0

диван

X₄

0

1

1

1

0

стол *

X₅

0

0

0

1

1

Рассчитываем значение переменной b аналогично методу расчета переменной a, используя значения матрицы, полученной в п.4:

B (количество совпадений отсутствия признаков у исследуемого объекта и эталона X_j)

окно

X₁

1

шкаф

X₂

2

стул

X₃

1

диван

X₄

1

5. Аналогичным образом рассчитывает переменные g и h по формулам

, :

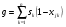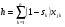G

H

окно

X₁

1

1

шкаф

X₂

0

0

стул

X₃

1

1

диван

X₄

2

1

6. Проверяем правильность произведенных расчетов по формуле:

a + b + g + h = n

где n – количество анализируемых признаков (в нашем случае n = 5)

a

b

g

h

n

2

1

1

1

5

3

2

0

0

5

2

1

1

1

5

1

1

2

1

5

Следовательно, расчеты произведены верно.

7. Рассчитываем значения функций сходства с каждым эталонным образом по формулам Рассела и Рао, Жокара и Нидмена, Дайса, Сокаля и Снифа, Сокаля и Мишнера, Кульжинского, Юла:

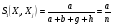(функция сходства Рассела и Рао),

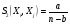(функция сходства Жокара и Нидмена),

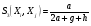(функция сходства Дайса),

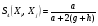(функция сходства Сокаля и Снифа),

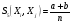(функция сходства Сокаля и Мишнера),

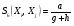(функция сходства Кульжинского),

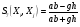(функция сходства Юла).

Рассела и Рао

Жокара и Нидмена

Дайса

Сокаля и Снифа

Сокаля и Мишнера

Кульжинского

Юла

Эталоны

0,4

0,5

0,333333

0,333333

0,6

1

0,333333333

окно

0,6

1

0,5

1

1

#ДЕЛ/0!

1

шкаф

0,4

0,5

0,333333

0,333333

0,6

1

0,333333333

стул

0,2

0,25

0,2

0,142857

0,4

0,33333

-0,333333333

диван

При распознавании образов с помощью функций сходства, исследуемый образ можно отнести к эталону, если значение функции сходства между ними максимально. Следовательно, наиболее близким эталоном к исследуемому образу является «шкаф», «стул», «окно».

8. Рассчитаем расстояние по Хеммингу между исследуемым образом и эталонами Расстояние по Хеммингу между двумя двоичными векторами равно числу несовпадающих двоичных компонент векторов. Используя переменные g и h его можно рассчитать по следующей формуле:

S_H = g + h

S_H = g + h

Окно

X₁

2

Шкаф

X₂

0

Стул

Х₃

2

Диван

X₄

3

При распознавании образов с помощью вычисления расстояния между объектами в качестве критерия принятия решения о принадлежности к конкретному эталону используется минимальное расстояние от исследуемого образа до эталона. Согласно данному критерию, наиболее близким к исследуемому образу является эталон «шкаф», «стул», «окно».

ВЫВОД: В результате проведенного анализа, согласно всех используемых функций сходства и расстояния по Хеммингу, исследуемый образ «стол» имеет наибольшее сходство с эталоном «шкаф», «стул», «окно».

9. Используя знания о логическом смысле переменных a, b, g, h предлагаю следующий вариант функции сходства:

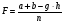
Используя её для оценивания сходства между исследуемым образом и эталонами, получим:

Эталоны

Предложенная функция

Окно

0,4

Шкаф

1

Стул

0,4

Диван

0,2

Как видим, результат предложенный функции совпадает с результатами функций Рассела и Рао, Жокара и Нидмена, Дайса, Сокаля и Снифа, Сокаля и Мишнера, Кульжинского, Юла, что свидетельствует о её достаточной достоверности.