Теория принятия решений: математические методы для выбора специалиста на должность администратора сети
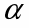
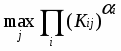
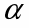
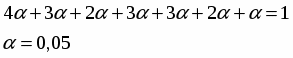
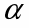
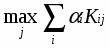
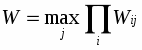
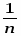
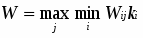
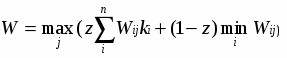
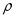
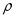
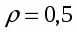
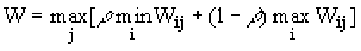
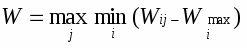
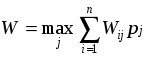
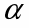 Теория принятия решений: математические методы для выбора специалиста на должность администратора сети
Теория принятия решений: математические методы для выбора специалиста на должность администратора сети
Домашнее задание
Выполнила студентка группы ИУ5-81 Выломова Е.А.
Московский государственный технический университет имени Н.Э.Баумана
Москва – 2006
На основании знаний современных технологий выполняет работы по проектированию сети, монтажу, настройке и обслуживанию сетевого оборудования. Осуществляет выбор сетевой операционной системы (совместно с руководством ЦИТ). Определяет средства вычислительной техники для создания локальной сети, ее структуру, макеты и схемы хранения и обработки информации, методы контроля. Предлагает технологии решения задач по всем этапам обработки информации.
Разрабатывает инструкции по работе в сети, оформляет необходимую техническую документацию. Определяет возможность использования готовых программных продуктов. Выполняет работу по унификации и типизации вычислительных процессов.
Установка сетевой ОС
Настройка рабочих параметров сетевой ОС
Установка клиентского ПО на рабочей станции
Настройка рабочих параметров клиентского ПО
Создание пользователей сети и установка режима их работы
Создание сценариев регистрации для пользователей
Создание меню для организации эффективной работы пользователей сети
Организация защиты информации на сервере
Обеспечение отказоустойчивой работы сервера
Организация печати в сети
Архивация информации в сети
Организация антивирусной защиты в сети
Установка ПО, расширяющего функциональные возможности сетевой ОС
Настройка рабочих параметров программного обеспечения, расширяющего функциональные возможности сетевой ОС
Диагностика кабельной системы
Сбор статистических данных о работе сети
Установка и настройка рабочих параметров ПО управления работой сети
Создание формализованной схемы работы сети. Разработка аналитической или имитационной модели , проведение экспериментов на этих моделях
Обработка результатов экспериментов с целью выбора наилучшего варианта модернизации или реорганизации сети
Проведение работы по модернизации и реорганизации сети
Требования к специалисту на должность администратора сети
Приведем некоторые примеры требований:
Работодатель №1:
Опыт построения и сопровождения программных/аппаратных комплексов
Общие знания ОС Windows и основных сетевых протоколов.
Опыт построения ЛВС, телефонных сетей, работы с АТС, построения и сопровождения сетевой инфраструктуры.
Опыт работы с оборудованием Cisco.
Работодатель №2:
Опыт администрирования оборудования Cisco (коммутаторы, маршрутизаторы) настройка, эксплуатация, мониторинг.
Знание основ взаимодействия сетевых устройств (Ethernet, TCP/IP), выявление слабых мест построения сети, перегрузок, устранение неисправностей.
Знание протоколов маршрутизации
Опыт построения и администрирования VPN, знание основ сетевой безопасности и криптозащиты
Знание проприетарных технологий и протоколов Cisco
Опыт эксплуатации и администрирования систем управления сетевым оборудованием.
Работодатель №3:
Знание стека протоколов TCP/IP, понимание модели OSI;
Понимание адресации в сетях, статической и динамической маршрутизации;
Знание средств сетевой диагностики, навыки обнаружения и устранения неисправностей в сетях передачи данных;
Опыт работы с оборудованием Cisco, Allied Telesyn;
Опыт администрирования и работы со службами ОС LInux, FreeBSD.
Работодатель №4:
Знание системного программного и аппаратного обеспечения (операционные системы, сервисные утилиты);
Опыт управление системами, базовым прикладным ПО/пакетами, включая бизнес-приложения, эл.почту и т.д.;
Опыт администрирования локальной вычислительной сети и сетевых сервисов (принтеры, базы данных, эл.почта);
Знание сегментов внутренней и глобальной сети (коммутационные концентраторы, шлюзы, маршрутизаторы, протоколы и т.д.);
Опыт мониторинг и протоколирования работы сети и сетевых служб.
В результате получаем список наиболее частых и важных требований к сетевому администратору:
Знание оборудования Cisco
Знание сетевой ОС
Знание стека протоколов TCP/IP
Опыт построения и администрирования ЛВС и сервисов
Понимание маршрутизации
Знание сегментов сети
Опыт мониторинга и протоколирования работы сети
Иванов И.И.
Петров П.П.
Сидоров С.С.
Знание Cisco
4
5
3
4
Знание сетевой ОС
3
2
5
1
Знание стека TCP/IP
2
3
4
4
ЛВС
3
5
3
2
Понимание маршрутизации
3
1
2
5
Знание сегментов сети
2
3
4
4
Опыт мониторинга
1
4
2
4
Построим матрицу доходов:
Иванов И.И.
Петров П.П.
Сидоров С.С.
Знание Cisco
20
12
16
Знание сетевой ОС
6
15
3
Знание стека TCP/IP
6
8
8
ЛВС
15
9
6
Понимание маршрутизации
3
6
15
Знание сегментов сети
6
8
8
Опыт мониторинга
4
2
4
Критерий принятия решений - это функция, выражающая предпочтения лица, принимающего решения (ЛПР), и определяющая правило, по которому выбирается приемлемый или оптимальный вариант решения.
Всякое решений в условиях неполной информации принимается в с учетом количественных характеристик ситуаций, в которой принимаются решения. Наиболее часто принимаются следующие критерии принятия Севиджа, критерий Гурвица, критерий Ходжа-Лимона, критерий Гермейера, соответствии с решений: минимаксный критерий, критерий Байеса-Лапласа, критерий какой-либо оценочной информацией, выбор которой должен осуществляться критерий произведений, составной критерий Байеса-Лапласа минимаксный.
Эти критерии можно использовать поочередно, причем после вычисления их значений среди нескольких вариантов приходится произвольным образом выделять некоторое окончательное решение. Что позволяет, во-первых, лучше проникнуть во все внутренние связи проблемы принятия решений и, во-вторых, ослабить влияние субъективного фактора.
Классические критерии принятия решений.
Методический учет таких факторов базируется на формировании специальных критериев, на основе которых принимаются решения. Критерии Вальда, Сэвиджа, Гурвица и Лапласа уже давно и прочно вошли в теорию принятия решений.
В соответствии с критерием Вальда в качестве оптимальной выбирается стратегия, гарантирующая выигрыш не меньший, чем "нижняя цена игры с природой":
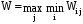 Правило выбора решения в соответствии с критерием Вальда можно интерпретировать следующим образом: матрица решений [Wir] дополняется еще одной строкой из наименьших результатов Wir каждой строки. Выбрать надлежит тот вариант, в столбце которого стоит наибольшее значение Wir этой строки.
Правило выбора решения в соответствии с критерием Вальда можно интерпретировать следующим образом: матрица решений [Wir] дополняется еще одной строкой из наименьших результатов Wir каждой строки. Выбрать надлежит тот вариант, в столбце которого стоит наибольшее значение Wir этой строки.
Выбранное таким образом решение полностью исключает риск. Это означает, что принимающий решение не может столкнуться с худшим результатом, чем тот, на который он ориентируется. Какие бы условия Vj не встретились, соответствующий результат не может оказаться ниже W. Это свойство заставляет считать критерий Вальда одним из фундаментальных. Поэтому в технических задачах он применяется чаще всего как сознательно, так и неосознанно. Однако в практических ситуациях излишний пессимизм этого критерия может оказаться очень невыгодным.
Применение этого критерия может быть оправдано, если ситуация, в которой принимается решение, характеризуется следующими обстоятельствами:
о вероятности появления состояния Vj ничего не известно;
с появлением состояния Vj необходимо считаться;
реализуется лишь малое количество решений;
не допускается никакой риск.
Иванов И.И.
Петров П.П.
Сидоров С.С.
Знание Cisco
20
12
16
Знание сетевой ОС
6
15
3
Знание стека TCP/IP
6
8
8
ЛВС
15
9
6
Понимание маршрутизации
3
6
15
Знание сегментов сети
6
8
8
Опыт мониторинга
4
2
4
3
2
3
Max=3 Следовательно, выбираем 1 или 3 варианты(Иванов И.И., Сидоров С.С.)
Критерий Байеса-Лапласа в отличие от критерия Вальда, учитывает каждое из возможных следствий всех вариантов решений:
Соответствующее правило выбора можно интерпретировать следующим образом: матрица решений [Wij] дополняется еще одной строкой, содержащей математическое ожидание значений каждого из столбцов. Выбирается тот вариант, в стролбцах которого стоит наибольшее значение Wir этой строки.
Критерий Байеса-Лапласа предъявляет к ситуации, в которой принимается решение, следующие требования:
вероятность появления состояния Vj известна и не зависит от времени;
принятое решение теоретически допускает бесконечно большое количество реализаций;
допускается некоторый риск при малых числах реализаций.
Иванов И.И.
Петров П.П.
Сидоров С.С.
Знание Cisco
20
12
16
Знание сетевой ОС
6
15
3
Знание стека TCP/IP
6
8
8
ЛВС
15
9
6
Понимание маршрутизации
3
6
15
Знание сегментов сети
6
8
8
Опыт мониторинга
4
2
4
8,57
8,57
8,57
Оптимального варианта не найдено
В соответствии с критерием Сэвиджа в качестве оптимальной выбирается такая стратегия, при которой величина риска принимает наименьшее значение в самой неблагополучной ситуации:
Здесь величину W можно трактовать как максимальный дополнительный выигрыш, который достигается, если в состоянии Vj вместо варианта Ui выбрать другой, оптимальный для этого внешнего состояния, вариант.
Соответствующее критерию Сэвиджа правило выбора следующее: из каждого элемента матрицы решений [Wij] вычитается наибольший результат max Wij соответствующей строки. Разности образуют матрицу остатков. Эта матрица пополняется строкой наименьших разностей Wir. Выбирается тот вариант, в столбце которого стоит наибольшее значение.
Иванов И.И.
Петров П.П.
Сидоров С.С.
Знание Cisco
20
12
16
20
Знание сетевой ОС
6
15
3
15
Знание стека TCP/IP
6
8
8
8
ЛВС
15
9
6
15
Понимание маршрутизации
3
6
15
15
Знание сегментов сети
6
8
8
8
Опыт мониторинга
4
2
4
4
Матрица остатков:
Иванов И.И.
Петров П.П.
Сидоров С.С.
Знание Cisco
0
-8
-4
Знание сетевой ОС
-9
0
-12
Знание стека TCP/IP
-2
0
0
ЛВС
0
-6
-9
Понимание маршрутизации
-12
-9
0
Знание сегментов сети
-2
0
0
Опыт мониторинга
0
-2
0
Min
-12
-9
-12
Max=-9 Следовательно, выбираем 2 вариант(Петров П.П.)
Согласно критерию Гурвица выбирается такая стратегия, которая занимает некоторое промежуточное положение между крайним пессимизмом и оптимизмом:
, где - коэффициент пессимизма, выбираемый в интервале [0,1].
Правило выбора согласно этому критерию следующее: матрица решений [Wij] дополняется столбцом, содержащим средние взвешенные наименьшего и наибольшего результатов для каждой строки. Выбирается тот вариант, в строках которого стоят наибольшие элементы Wir этого столбца.
При = 1 критерий Гурвица превращается в критерий Вальда (пессимиста), а при = 0 - в критерий азартного игрока. Отсюда ясно, какое значение имеет весовой множитель . В технических приложениях правильно выбрать этот множитель бывает так же трудно, как правильно выбрать критерий. Поэтому чаще всего весовой множитель = 0.5 принимается в качестве средней точки зрения.
Критерий Гурвица предъявляет к ситуации, в которой принимается решение, следующие требования:
о вероятности появления состояния Vj ничего не известно;
с появлением состояния Vj необходимо считаться;
реализуется лишь малое количество решений;
допускается некоторый риск.
Иванов И.И.
Петров П.П.
Сидоров С.С.
Знание Cisco
20
12
16
Знание сетевой ОС
6
15
3
Знание стека TCP/IP
6
8
8
ЛВС
15
9
6
Понимание маршрутизации
3
6
15
Знание сегментов сети
6
8
8
Опыт мониторинга
4
2
4
3
2
3
Max
20
15
16
Min*
1,5
1
1,5
Max*(1-)
10
7,5
8
SUMM
11,5
8,5
9,5
Max=11,5 Следовательно, выбираем 1 вариант(Иванов И.И.)
Критерий Ходжа-Лемана базируется одновременно на критериях Вальда и Байеса-Лапласа:
Правило выбора, соответствующее этому критерию, формулируется следующим образом: матрица решений [Wij] дополняется строкой, составленной из средних взвешенных (с постоянными весами) математического ожидания и наименьшего результата каждого стролбца. Отбирается тот вариант решения, в стролбце которого стоит наибольшее значение этой строки.
При z=1 критерий преобразуется в критерий Байеса-Лапласа, а при z=0 превращается в критерий Вальда. Таким образом, выбор параметра z подвержен влиянию субъективизма. Кроме того, без внимания остается и число реализаций. Поэтому этот критерий редко применяется при принятии технических решений.
Критерий Ходжа-Лемана предъявляет к ситуации, в которой принимается решение, следующие требования:
о вероятности появления состояния Vj ничего не известно, но некоторые предположения о распределении вероятностей возможны;
принятое решение теоретически допускает бесконечно большое количество реализаций;
допускается некоторый риск при малых числах реализаций.
Z=0,5
Иванов И.И.
Петров П.П.
Сидоров С.С.
Знание Cisco
20
12
16
Знание сетевой ОС
6
15
3
Знание стека TCP/IP
6
8
8
ЛВС
15
9
6
Понимание маршрутизации
3
6
15
Знание сегментов сети
6
8
8
Опыт мониторинга
4
2
4
3
2
3
MX
8,57
8,57
8,57
Min*(1-Z)
1,5
1
1,5
MX*Z
4,28
4,28
4,28
SUMM
5,78
5,28
5,78
Max=5,78 Следовательно, выбираем 1 или 3 варианты(Иванов И.И., Сидоров С.С.)
Этот критерий ориентирован на величину потерь
Правило выбора согласно критерию Гермейера формулируется следующим образом:
матрица решений Wij дополняется ещё одной строкой содержащей в каждом стролбце наименьшее произведение имеющегося в нем результата на вероятность соответствующего состояния. Выбираются те варианты в стролбцах которых находится наибольшее значение Wij этой строки.
В случае равномерного распределения kj = .
Условия его применимости таковы :
вероятности появления состояния неизвестны;
с появлением тех или иных состояний, отдельно или в комплексе, необходимо считаться;
допускается некоторый риск;
решение может реализоваться один или несколько раз.
Если функция распределения известна не очень надёжно, а числа реализации малы, то, следуя критерию Гермейера, получают, вообще говоря, неоправданно большой риск.
Иванов И.И.
Петров П.П.
Сидоров С.С.
Знание Cisco
20
12
16
Знание сетевой ОС
6
15
3
Знание стека TCP/IP
6
8
8
ЛВС
15
9
6
Понимание маршрутизации
3
6
15
Знание сегментов сети
6
8
8
Опыт мониторинга
4
2
4
Иванов И.И.
Петров П.П.
Сидоров С.С.
Знание Cisco
2,85
1,7
2,28
Знание сетевой ОС
0,85
2,14
0,42
Знание стека TCP/IP
0,85
1,14
1,14
ЛВС
2,14
1,28
0,85
Понимание маршрутизации
0,42
0,85
2,14
Знание сегментов сети
0,85
1,14
1,14
Опыт мониторинга
0,57
0,28
0,57
0,42
0,28
0,42
Max=0,42 Следовательно, выбираем 1 или 3 варианты(Иванов И.И., Сидоров С.С.)
Правило выбора в этом случае формулируется так :
Матрица решений Wij дополняется новой строкой, содержащей произведения всех результатов каждого стролбца. Выбираются те варианты, в столбцах которых находятся наибольшие значения этой строки.
Применение этого критерия обусловлено следующими обстоятельствами :
вероятности появления состояния неизвестны;
с появлением каждого из состояний по отдельности необходимо считаться;
критерий применим и при малом числе реализаций решения;
некоторый риск допускается.
Иванов И.И.
Петров П.П.
Сидоров С.С.
Знание Cisco
20
12
16
Знание сетевой ОС
6
15
3
Знание стека TCP/IP
6
8
8
ЛВС
15
9
6
Понимание маршрутизации
3
6
15
Знание сегментов сети
6
8
8
Опыт мониторинга
4
2
4
PROIZVED
777600
829440
1105920
Max=1105920 Следовательно, выбираем 3 вариант(Сидоров С.С.)
Общие рекомендаций по выбору того или иного критерия дать затруднительно. Однако отметим следующее: если в отдельных ситуациях не допустим даже минимальный риск, то следует применять критерий Вальда; если определенный риск вполне приемлем, то можно воспользоваться критерием Сэвиджа. Можно рекомендовать одновременно применять поочередно различные критерии. После этого среди нескольких вариантов, отобранных таким образом в качестве оптимальных, приходится волевым решением выделять некоторое окончательное решение.
Такой подход позволяет, во-первых, лучше проникнуть во все внутренние связи проблемы принятия решений и, во-вторых, ослабляет влияние
субъективного фактора. Кроме того, в области технических задач различные критерии часто приводят к одному результату.
Иванов И.И.
Петров П.П.
Сидоров С.С.
Знание Cisco
4
5
2
1
Знание сетевой ОС
3
2
4
4
Знание стека TCP/IP
2
1
4
4
ЛВС
3
3
3
2
Понимание маршрутизации
3
1
2
3
Знание сегментов сети
2
2
3
5
Опыт мониторинга
1
4
4
5
Нормированная матрица
Иванов И.И.
Петров П.П.
Сидоров С.С.
Знание Cisco
0,2
1
0,4
0,2
Знание сетевой ОС
0,15
0,3
0,6
0,6
Знание стека TCP/IP
0,1
0,1
0,4
0,4
ЛВС
0,15
0,45
0,45
0,3
Понимание маршрутизации
0,15
0,15
0,3
0,45
Знание сегментов сети
0,1
0,2
0,3
0,5
Опыт мониторинга
0,05
0,2
0,2
0,25
SUMM
2,4
2,65
2,3
Max=2,65 Следовательно, выбираем 2 вариант(Петров П.П.)
Иванов И.И.
Петров П.П.
Сидоров С.С.
Знание Cisco
0,2
1,38
1,14
1
Знание сетевой ОС
0,15
1,1
1,23
1,23
Знание стека TCP/IP
0,1
1
1,14
1,14
ЛВС
0,15
1,18
1,18
1,1
Понимание маршрутизации
0,15
1
1,1
1,8
Знание сегментов сети
0,1
1,07
1,11
1,17
Опыт мониторинга
0,05
1,07
1,07
1,08
PROIZVED
2,05
2,46
3,5
Max=3,5 Следовательно, выбираем 3 вариант(Сидоров С.С.)

Нравится материал? Поддержи автора!
Ещё документы из категории информатика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ