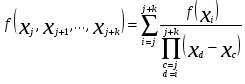
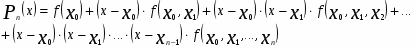
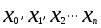
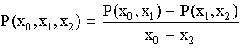
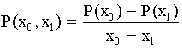
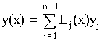
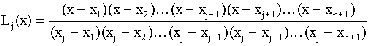
КУРСОВАЯ РАБОТА

по теме: "Вычислительная техника и программирование"

Киев

Введение

Если задана функция y(x), то это означает, что любому допустимому значению х сопоставлено значение у. Но нередко оказывается, что нахождение этого значения очень трудоёмко. Например, у(х) может быть определено как решение сложной задачи, в которой х играет роль параметра или у(х) измеряется в дорогостоящем эксперименте. При этом можно вычислить небольшую таблицу значений функции, но прямое нахождение функции при большом числе значений аргумента будет практически невозможно. Функция у(х) может участвовать в каких-либо физико-технических или чисто математических расчётах, где её приходится многократно вычислять. В этом случае выгодно заменить функцию у(х) приближённой формулой, то есть подобрать некоторую функцию j(х), которая близка в некотором смысле к у(х) и просто вычисляется. Затем при всех значениях аргумента полагают у(х)"j(х).

Что касается критерия согласия, то классическим критерием согласия является "точное совпадение в узловых точках". Этот критерий имеет преимущество простоты теории и выполнения вычислений, но также неудобство из-за игнорирования шума (погрешности, возникающей при измерении или вычислении значений в узловых точках). Другой относительно хороший критерий — это "наименьшие квадраты". Он означает, что сумма квадратов отклонений в узловых точках должна быть наименьшей возможной или, другими словами, минимизирована. Этот критерий использует ошибочную информацию, чтобы получить некоторое сглаживание шума. Третий критерий связывается с именем Чебышева. Основная идея его состоит в том, чтобы уменьшить максимальное отклонение до минимума. Очевидно, возможны и другие критерии.

Цель задачи о приближении (интерполяции): данную функцию у(х) требуется приблизительно заменить некоторой функцией j(х), свойства которой нам известны так, чтобы отклонение в заданной области было наименьшим. интерполяционные формулы применяются, прежде всего, при замене графически заданной функции аналитической, а также для интерполяции в таблицах.

Один из подходов к задаче интерполяции — метод Лагранжа. Основная идея этого метода состоит в том, чтобы прежде всего найти многочлен, который принимает значение 1 в одной узловой точке и 0 во всех других. Легко видеть, что функция (1) является требуемым многочленом степени n; он равен 1, если X=Xj и 0, когда X=Xi, i¹j.

(1)

Многочлен Lj(x)×Yj принимает значения Yi в i-й узловой точке и равен 0 во всех других узлах. Из этого следует, что (2) есть многочлен степени n, проходящий через n+1 точку (Xi, Yi).

(2)

Другой подход — метод Ньютона (метод разделённых разностей). Этот метод позволяет получить аппроксимирующие значения функции без построения в явном виде аппроксимирующего полинома. В результате получаем формулу для полинома Pn, аппроксимирующую функцию f(x):

P(x)=P(x0)+(x-x0)P(x0,x1)+(x-x0)(x-x1)P(x0,x1,x2)+…+

(x-x0)(x-x1)…(x-xn)P(x0,x1,…,xn);

разделённая разность 1-го порядка;

разделённая разность 2-го порядка и т.д.

Значения Pn(x) в узлах совпадают со значениями f(x)

Фактически формулы Лагранжа и Ньютона порождают один и тот же полином, разница только в алгоритме его построения.

Постановка задачи:

1. Построить интерполяционный полином Ньютона по значениям функции в узлах: .

2. Математическая постановка задачи:

Формула выглядит так:

Разделённая разность:

.

1. Алгоритм программы Polinom

Рис.1 Схема алгоритма подпрограммы Swap

Рис.2 Схема алгоритма подпрограммы Null

Рис.3 Схема алгоритма подпрограммы Rise

Рис.4 Схема алгоритма подпрограммы Calculat

Рис.5 Схема алгоритма подпрограммы Vvod

Рис.6 Схема алгоритма программы Print_Polinom

Рис.7 Схема алгоритма подпрограммы Div_Res

Рис.8 Схема алгоритма программы Nuton

Рис.9 Схема алгоритма подпрограммы Recover

Рис.10 Блок-схема программы Polinom

2. Листинг программы Polinom

Реализуем алгоритм на языке высокого уровня Turbo Pascal, используя подпрограммы.

PROGRAM POLINOM; {Программа построения интерполяционного полинома Ньютона}

Uses Crt;

Const Max_Num_Usel=20; {Количество узлов}

Type

Matrix_Line = Array[1..Max_Num_Usel] Of Real;

Var Max:Byte;

X,F:Matrix_Line;

PROCEDURE Swap(Var First,Second:real); {Обмена двух REAL переменных}

Var Temp:Real;

Begin

Temp:=First;

First:=Second;

Second:=Temp;

End; {Swap}

FUNCTION Rise(Root:Real;Power:Integer):Real; {Возведение в степень}

Var Temp:Real;

i:Integer;

Begin

Temp:=1;

For i:=1 To Power Do

Temp:=Temp*Root;

Rise:=Temp;

End; {Rise}

PROCEDURE Null(Last:Byte;Var M:Matrix_Line); {Обнуление матриц}

Var i:Byte;

Begin

For i:=1 To Last Do

M[i]:=0;

End; {Null}

PROCEDURE Calculat(Num:Integer;Cx:Matrix_Line); {вычисление значений полинома}

Var x,y:Real;

i:Integer;

Finish:Boolean;

c:Char;

Begin

Writeln('***********************************************');

Writeln;

Writeln('Вычисление значений интерполяционного полинома:');

Writeln('~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~');

Writeln('Введите значение x:');

Repeat

y:=0;

Readln(x);

For i:=Num DownTo 1 Do

y:=y+Cx[i]*Rise(x,i-1);

Writeln('Значение полинома в точке Xo=',x:7:4,' равно Yo=',y:7:4);

Write('Нажмите `ESC` для выхода или любую клавишу для продолжения');

c:=Readkey;

If c=#27 Then Finish:=True Else Finish:=False;

GoToXY(1,WhereY-2);

DelLine; DelLine;DelLine;

Until Finish;

End; {Calculat}

PROCEDURE Vvod(Var Mat_x,Mat_f:Matrix_Line;Var Number:Byte);

Var c:Char;

i,j:Integer;

Enter:Boolean;

Begin

ClrScr;

Writeln('Построение интерполяционного полинома Ньютона по значениям функции в узлах');

Writeln('~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~);

Writeln;

Writeln('Введите кол-во узлов интерполяции (0<N<',Max_Num_Usel,'):');

Repeat

Readln(Number);

Until (Number

ClrScr;

Writeln('Значения узлов не должны сопадать');

Writeln('Введите значения узлов и значения функций в них:');

For i:=1 To Number Do

Begin

Repeat

{Ввод узлов}

Enter:=True;{Правильность ввода}

GoToXY(5,i+3);

Write('X(',i-1,')=');

Readln(Mat_x[i]);

For j:=i-1 DownTo 1 Do

If (Mat_x[j]=Mat_x[i]) Then {Проверка на одинаковые узлы}

Begin

Writeln('Значения узлов ',i,' и ',j,' введены неверно!!!');

Write('Нажмите `Y` для повторения ввода или любую клавишу для выхода');

c:=Readkey;

If (c='Y') Or (c='y') Then Enter:=False Else Halt;

GoToXY(5,i+3);

DelLine;DelLine;DelLine;

End;

Until Enter;

{Ввод значений функции в узлах}

GoToXY(35,i+3);

Write('Y(',Mat_x[i]:5:2,')=');

Readln(Mat_f[i]);

End;

{Сортировка узлов по возрастанию}

For i:=1 To Number Do

For j:=i To Number Do

If (Mat_x[j]

Begin

Swap(Mat_x[j],Mat_x[i]);

Swap(Mat_f[j],Mat_f[i]);

End;

End;{Vvod}

{Распечатка полинома}

PROCEDURE Print_Polinom(N:Integer;Cx:Matrix_Line);

Var i:Integer;

c:Char;

Begin

Writeln;

Writeln('Полином Ньютона:');

Write('P',N-1,'(x)=');

For i:=N DownTo 1 Do

If Round(Cx[i]*1000)<>0 Then{Если в числе не более 3х нулей после запятой,}

Begin {тогда выводим его на экран}

If (Cx[i]<0) Then Write(' - ') Else Write(' + ');

Write(ABS(Cx[i]):5:3);

If (i>2) Then Write('·x^',i-1) Else

If (i>1) Then Write('·x')

End;

Writeln;

Writeln;

Writeln('Нажмите `ESC` для выхода или любую клавишу для вычисления значения полинома');

c:=Readkey;

GoToXY(1,WhereY-1);

DelLine;DelLine;

If c<>#27 Then Calculat(N,Cx);

End;{Print_Polinom}

PROCEDURE Recover(Current,Number:byte; Var Result,Mat_X:Matrix_Line);

{Восстановление коэффициентов полинома по его корням}

Var Process,i,j,k:Integer;

Begin

{Заносим первый линейный множитель вида (X - Cn) в Result}

k:=2; {Количество коэффициентов в Result = 2}

If Current<>1 Then {Если исключаем не Х1, то Result[1] = X1}

Begin

Result[1]:=-Mat_X[1];

Process:=2 {Начнем обработку со второго множителя}

End

Else Begin {Иначе Result[1] = X2}

Result[1]:=-Mat_X[2];

Process:=3 {Начнем обработку с третьего множителя}

End;

Result[2]:=1; {В любом случае Result[2] = 1, т.к. все множители вида (X - Cn) }

For i:=Process To Number Do

If i<>Current Then

Begin

For j:=k DownTo 1 Do {Домнoжаем полученный полином на X}

Result[j+1]:=Result[j];

Result[1]:=0; {Поэтому C0 = 0}

For j:=1 To k Do {Домнoжаем полученный полином на Cn = -X[n]}

Result[j]:=Result[j]-Mat_X[i]*Result[j+1];

Inc(k); {Размерность полинома увеличилась}

End;

End; {Recover}

PROCEDURE Nuton(Number:Byte;Var Mat_x,Mat_f:Matrix_Line);

{Интерполяционная формула Ньютона }

Var i,j:integer;

Temp,Result:Matrix_Line;

C:real;

{Функция вычисления разделенной разности по начальному и конечному узлам}

Function Div_Res(Beg_Usel,Fin_Usel:Byte;Var Xn,Fn:Matrix_Line):real;

Begin

Beg_Usel:=Beg_Usel+1;

If Beg_Usel=Fin_Usel Then

Div_Res:=(Fn[Fin_Usel]-Fn[Beg_Usel-1])/(Xn[Fin_Usel]-Xn[Beg_Usel-1])

Else Div_Res:=(Div_Res(Beg_Usel,Fin_Usel,Xn,Fn)-Div_Res(Beg_Usel-1,Fin_Usel-1,Xn,Fn))/(Xn[Fin_Usel]-Xn[Beg_Usel-1]);

End; {Div_Res}

Begin {Nuton}

Null(Number,Result);

Null(Number,Temp);

For i:=2 To Number Do

Begin

Recover(Number+1,i-1,Temp,Mat_x);

c:=Div_Res(1,i,Mat_x,Mat_f); {Значение разделенной разности 1 и i-го узлов}

For j:=1 To i Do

Result[j]:=c*Temp[j]+Result[j];

End;

Result[1]:=Result[1]+Mat_f[1];

Print_Polinom(Number,Result)

End;{Nuton}

Begin{Main}

Null(Max_Num_Usel,X);

Null(Max_Num_Usel,F); {Начальное обнуление матриц}

Vvod(X,F,Max);

Nuton(Max,X,F);

End.{Main}

3. Пример работы программы

Чтобы проверить правильно ли у нас строится полином Ньютона, разложим какую-нибудь известную функцию. Например, y=sin(x) на интервале Х от 0.1 до 0.9. Полином будем строить по 5 точкам (шаг 0.2). Данные в программу вводим согласно таблице 1.

Таблица 1. Исходные значения для программы.

x

y(x)

0.1

0.0998

0.3

0.2955

0.5

0.4794

0.7

0.6442

0.9

0.7833

На инженерном калькуляторе вычисляем Sin(0.4)= 0.3894

Результаты работы программы:

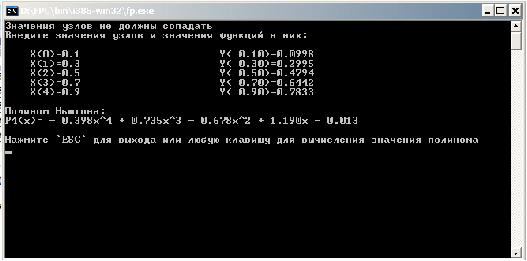
Построение интерполяционного полинома Ньютона по значениям функции в узлах

Введите кол-во узлов интерполяции (0<N<20): 5

Значения узлов не должны сопадать

Введите значения узлов и значения функций в них:

X(0)=0.1 Y( 0.10)=0.0998

X(1)=0.3 Y( 0.30)=0.2955

X(2)=0.5 Y( 0.50)=0.4794

X(3)=0.7 Y( 0.70)=0.6442

X(4)=0.9 Y( 0.90)=0.7833

Полином Ньютона:

P4(x)= + 0.018·x^4 - 0.181·x^3 + 0.005·x^2 + 0.99

Рисунок 11. Результат работы программы Polinom

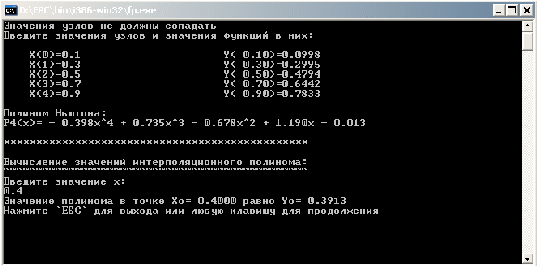
Вычисление значений интерполяционного полинома:

Введите значение x:

0.4

Значение полинома в точке Xo= 0.4000 равно Yo= 0.3894

Рисунок 12. Результат вычисления значения полинома

Заключение

Появление и непрерывное совершенствование ЭВМ привело к революционному преобразованию науки вообще и математики в особенности. Изменилась технология научных исследований, увеличились возможности теоретического изучения, прогноза сложных процессов, проектирования инженерных конструкций. Но более сложные расчёты требуют и более глубокого знакомства с численными методами. Численные методы носят в основном приближённый характер, позволяя, тем не менее, получить окончательный числовой результат с приемлемой для практических целей точностью.

Выполняя курсовую работу, я познакомилась с понятием интерполяция, укрепила свои знания в программировании на языке Turbo Pascal и при оформлении курсовой работы получила практические навыки при работе в пакетах Microsoft Word и Microsoft Visio.