Численные методы и их реализация в Excel
Кыргызский Государственный Национальный Университет Институт Интеграции Международных Образовательных Программ Кыргызско - Американский факультет Компьютерных технологий и ИНТЕРНЕТ


КГНУ
Институт Интеграции Международных Образовательных Программ
по предмету: ‘’Моделирование ’’
на тему: ‘’Численные методы и их реализация в Excel’’
Выполнила: студентка 3-курса
Камчыбекова Б.
гр. КИС-5-97
Проверил: к.т.н. профессор. Бабак В. Ф.
Бишкек – 2000
Глава 1. Подбор параметра…
1.1. Нелинейные алгебраические уравнения
При моделировании экономических ситуаций часто приходится решать уравнение вида:
f (x, p1, p2 ,…, pn)=0 (1)
где f-заданная функция, х-неизвестная переменная.
p1, p2,…, pn – параметры модели.
Решение таких уравнений может быть как самостоятельной, так и частью более сложных задач. Как правило, исследователя интересует поведение решения в зависимости от параметров pk , k=1,n
Решениями или корнями уравнения (1) называют такие значения переменной х, которые при подстановке в уравнение обращают его в тождество.
Только для линейных или простейших нелинейных уравнений удается найти решение в аналитической форме, т.е. записать формулу, выражающую искомую величину х в явном виде через параметры pk (например формула корней квадратного уравнения).
В большинстве же случаев приходится решать уравнение (1) численными методами, в которых процедура решения задается в виде многократного применения некоторого алгоритма. Полученное решение всегда является приближенным, хотя может быть сколь угодно близко к точному.
Рассмотрим последовательность действий для получения решения нелинейного уравнения в среде электронной таблицы.
Пусть надо решить уравнение вида:
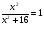 (2)
(2)
Cформируем лист электронной таблицы, как показано на рис.1. Уравнение (2) запишем в клетку С5, начиная со знака равенства, а вместо переменной x укажем адрес клктки В5, которая содержит значение начального приближения решения.
вместо переменной x укажем адрес клетки В5. которая содержит значение начального приближения решения
Метод, применяемый в EXCEL для решения таких уравнений -модифицированный конечными разностями метод Ньютона, который позволяет не сильно заботится о начальном приближении, как этого требуют другие численные методы решения уравнений (метод хорд, дихотомии и др.) Единственно, что следует учесть - это то, что будет' найдено решение ближайшее к выбранному начальному приближению.
Для получения решения уравнения (2) надо выполнить следующую последовательность действий:
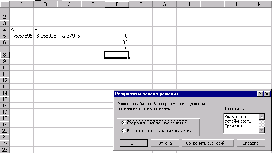
1. Выполнить команду Сервис/Подбор параметра... (получим лист электронной таблицы, как показано на Рис. 2);
2. Заполнить диалоговое окно Подбор параметра...:
2,1 Щелкнуть левой клавишей мыши в поле Установить в ячейке, после появления в нем курсора, переместить указатель мыши и щелкнуть на клетке с формулой, в нашем случае это клетка С5, абсолютный адрес которой $С$5 появится в поле рис.1
Этот адрес можно было бы набрать на клавиатуре, после появления курсора в поле. Установить в ячейке
2.2. В поле Значение ввс
В нашем случае это значение равно О.
2.3 В поле, Изменяя значение ячейки ввести адрес клетки, где задано начальное приближение решения, в нашем случае это клетка В 5 (абсолютный адрес которой $В$5 появится в поле после щелчка левой клавиши мыши на клетке В5).После выполнения пунктов 1-2 страница электронной таблицы будет выглядеть так, как показано на Рис.3.
Правая часть решаемого уравнения не обязана быть всегда нулем равнение (2) преобразовать к виду 10*х*(х+10)/(х-9)=2. то в поле Значение следовало бы установить 2.
После нажатия на кнопке ОК появится окно Результат подбора параметра, в котором дается о том нацдена ли решение, чему равна и какова точность полученного решения.
Для нашего примера Результат подбора параметра показан на Рис.4
При значении аргумента –0,187204141 функция, стоящая в левой части уравнения (2) отличается от нуля на – 0,000484158.
Достигнутая точность решения равна – 1.0Е-3
Если полученные значения следует "отразить на листе электронной таблицы, то надо щелкнуть на кнопке ОК . .если же нет то на кнопку Отмена. В первом случае найденные значения зафиксируются в клетках В5 и С5 и лист электронной таблицы будет выглядеть как на Рис.5, или как на Рис.6, если установить режим отображения результатов, предварительно сняв режим отображения формул, выполнив команду Сервис/Параметры/Вид/Формулы.
Численные методы решения уравнений хороши тем, что мoжно получить приближенное решение с заданной точностью. EXCEL име (возможность управлять выбором точности. Для этого надо выполни' команду Сервис/Параметры/Вычисления и в соответствующих полз установить. значения относительной погрешности и количества итераш Рис.7
1.2 Системы двух линейныхалгебраических уравнений
Вышеизложенный способ получения решения уравнения может быть легко распрастранен для случая решения ситемы двух уравнений с двумя неизвестными, если ситема имеет следующий вид.
Y=Ф (х)
Y=(х)
В каждом уравнении системы функции у явна выражена через х
Преобразуем систему (3) в одно уравнение вида (+)
Ф (х) -'^(х) = 0 - (4)
Полученное уравнение уже можно решить с помощью Подбора параметра... так как это было описано выше.
В качестве примера рассмотрим нахождение равновесных цены и объема продаж для рынка некоторого товара.
Пусть функция спроса на товар имеет вид Q = 40/(Р+3) а функция предложения: Q = 20Р-14
Найти равновесные цену и объем , построить графики спроса и предложения.
Имеющуюся систему уравнений Q=40/(p+3)
Q=20Р-14
преобразуем в одно уравнение вида 40 / (р + 3) - 20 р +14=0
Подбором параметра... описанным выше, находим равновесную цену, она равна 1,17, подставив это значение в одно из уравнений системы, получим и значение равновесного объема - 9,57. Для построения графика, иллюстрирующего ситуацию равновесия спроса и предложения на рынке, воспользуемся знанием равновесной цены и возьмем значения цен в некоторой окрестности от нее. например от 0 до 4 с шагом 0,1.
Используя все возможности мастера диаграмм, получим следующую иллюстрацию решения задачи о равновесии на рынке. Рис.8.
Задание1
Найти ближайшее к начальному приближению решение следующих уравнений. Исследовать влияние начального приближения на найденное решение
10x-x+56=12
Задание 2
Подбором параметра... найти точку равновесия рынка некоторого товара, для чего решить систему уравнений, описывающих спрос и предложение этого товара. Построить и оформить график равновесия.
Функция спроса
Q=50e-3
Функция предложения
Q=3p-4e
0<p<20
Глава 2. Матричная алгебра
По мнению крупнейшего экономиста нашей эпохи В.В.Леонтьева. «Дифференциальное исчисление и элементарная алгебра - два традиционных инструмента экономиста-математика заменяются . или, по крайней мере дополняются матричной алгеброй.»4Матричная алгебра тесно связана с линейными функциями и с линейными ограничениями в связи с чем находит себе применение в различных экономических задачах:
• в эконометрике, для оценки параметров множественных линейных регрессий;
• при решении задач линейного программирования;
• при макроэкономическом моделировании и т.д. Особое отношение к матричной алгебре в экономике появилось после создания моделей типа «Затраты - Выпуск», где с помощью матриц технологических коэффициентов объясняется уровень производства в каждой отрасли через связь с соответствующими уровнями во всех прочих отраслях.
Электронная таблица EXCEL имеет ряд встроенных функций для работы с матрицами:
ТРАНСП - транспонирование исходной матрицы - вычисление определителя квадратной матрицы
МОПРЕД- вычисление определителя квадратной матрицы
МОБР - вычисление матрицы обратной к данной - нахождение матрицы, являющейся произведением двух матриц.Кроме того возможно выполнение операций поэлементного сложения (вычитания ) двух матриц и умножения (деления) матрицы на число. Все вышеперечисленные функции вызываются через мастер функций и хотя относятся к разделу математических, они располагаются в полном алфавитном перечне.
МУМНОЖ- нахождение матрицы, являющейся произведением двух матриц.
Кроме того возможно выполнение операций поэлементного сложения (вычитания ) двух матриц и умножения (деления) матрицы на число.
Все вышеперечисленные функции вызываются через мастер функций и хотя относятся к разделу математических , они располагаются в полном алфавитном перечне.
2.1 Определитель матрицы
Для вычисления определителя матрицы сформируем лист электронной таблицы, как показано на Рис.9. Место записи вычисленного определителя матрицы определяется местоположением табличного курсора.
Пусть на листе электронной таблицы сделаны все предварительные действия, т.е введена матрица, над которой будут производиться действия и определено место записи результата.
Следующим шагом вызывается мастер функций рис10., левое окно которого содержит перечень разделов , а правое алфавитный список функций, составляющих данный раздел.
В левом окне выбираем раздел -« Полный алфавитный перечень «, а в правом МОПРЕД , В появившемся диалогом окне Рис11. Следует указать левый верхний и через двоеточие правый нижний адреса матрицы, (или обвести интересующую нас матрицу, при нажатой клавиши мыши, штриховой линией, что автоматизирует процесс определения адресов местоположения матрицы на листе ЭТ) Рис.11
Щелкнув на кнопке Готово получим значение определителя, размещенного в клетке С10. Его значение равно 1 Нахождение определителя - это единственное действие .над матрицей, которое дает в результате число, остальные матричные функции в результате своих действий дают матрицы и , это,следует, учитывать при подготовке на листе ЭТ места для размещения результата.
2.2 Умножение матриц
В качестве примера рассмотрим умножение двух матриц. Пусть надо умножить матрицу А(5*4) на матрицу В(4*3). это умножение возможно, так как число столбцов матрицы А совпадает с числом строк матрицы В . результатом будет матрица С(5*3).
Перед вызовом функции умножения матриц сформируем лист ЭТ, так как показано на Рис.12
Затем выполним следующую последовательность действий:
1.Зададим матрицу А
2. Зададим матрицу В
3 Отметим место для матрицы С7
4. Обратимся к мастеру функций , найдем в полном алфавитном перечне функцию МУМНОЖ и выполним постановку задачи так. Как показано на Рис. 13
В качестве массива 1 указывается диапазон адресов матрицы А, а в качестве массива 2- диапаон адресов матрицы В.
Щелкнуть в на кнопке Готово получим в клетке, где присутствует знак равенства, полную запись функции умножения. Для получения результата необходимо нажать клавиши Shift/Ctrl/Enter одновременно8
7В выделенном под результат месте ЭТ поставить знак равенства.
8Все матричные функции, за исключением вычисления определителя. требуют заключительного одновременного нажатия клавиш Shift/Ctrl/Enter
На Рис 15 показан результат умножения после нажатия клавш Shift/Ctrl/Enter, а в строке формул стоит выражение в "фигурны скобках, {3*B4:D6} что является признаком выполнения матрично операции
Сложение матриц
Для сложения двух матриц одинаковой размерности10 следует выполнить следующую последовательность действий. . Задать две исходных матрицы. . Отметить место для матрицы - результата. • . В выделенном под результат месте ЭТ поставить знак равенства и записать сумму так. как показано на Рис. 16. . -Завершить выполнение работы нажатием клавиш Shift/Ctrl/Enter, Рис.17".
Фигурные скобки в строке формул {В4:D6+F4:H6}-признак выполнения матричной операции
Задание 3
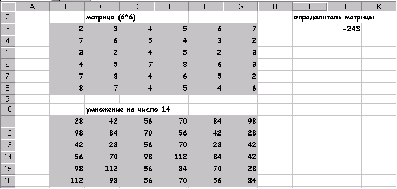
Найти определитель матрицы В (6*6):. умножить матрицу на 14.
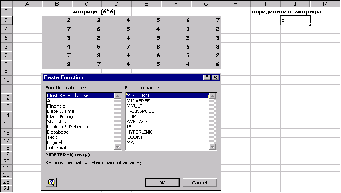
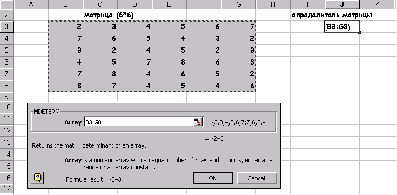

Умножение на число 14

результат:
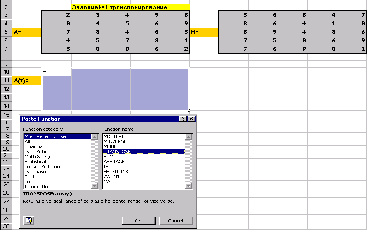
Задание 4
Транспонирование матрицы А :
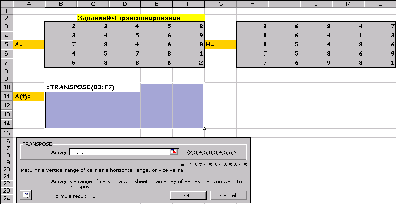
После нажатия Shift/Ctrl/Alt:
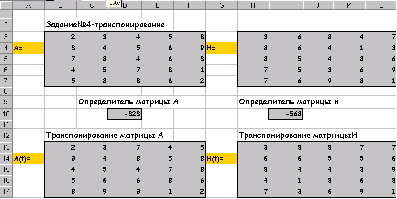
Умножение матриц А на H(t):
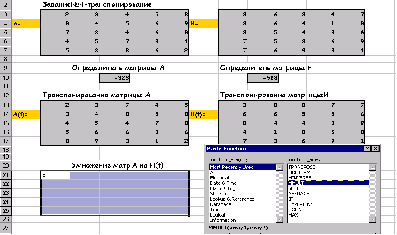
После нажатия на ОК:
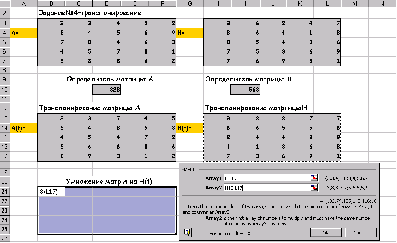
Вычитание матриц AH(t) и HA(t):

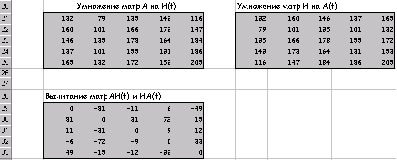
2.6 Система линейных алгебраических уравнений
Решение Система линейных алгебраических уравнений всегда занимало математиков и для решения было разработано немало численных методов, подразделяющихся на прямые ( Гаусса, Кремера) и итерационные (простых итераций , Зейделя ,верхних релакций… )
EXCEL задача получения решение СЛАУ решаются с помощью вышеописанных матричных функций, для чего исходную систему надо представить в виде матричного уравнения.
Рассмотрим последовательность действий для получения решение СЛАУ на конкретном примере.
Задание 5
Найти решение системы линейных алгебраических уравнение и сделать проверку.
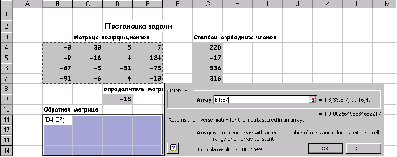
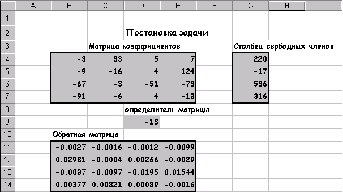
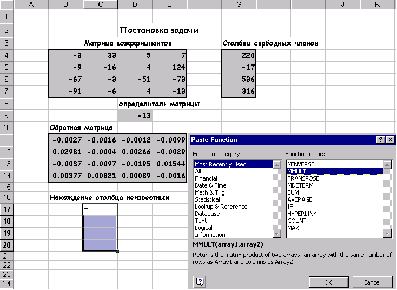
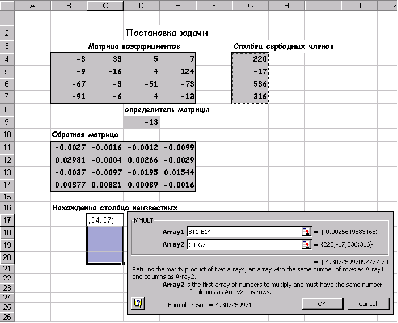
Для того, чтобы система (5) имела единственное решение необходимо и достаточно, чтобы определить системы, составленный из коэффициентов при переменных х,х,х,х, не был равен нулю.
Рассчитаем определить системы пользуясь функцией МОПРЕД. Рассчитанное значение определителя системы равно 1662723продолжать процесс поиска решения.
Из линейной алгебры известна матричная запись системы уравнений и матричное преставление решения.
Перепишем систему уравнений (5):
Тогда матричное решение уравнения выглядит так:
Результат, указанный на рис18 можно получить, выполнив следующие действия:
Вычислить определитель и выяснить имеет ли система единственное решение.
Вычислить матрицу обратную к исходной.
Найти произведение обратной матрицы и вектор столбца свободных членов.
Глава3. Поиск решения…
1.2Оптимизация
Почти любую ситуацию , встречающуюся в деловой личной общественной жизни можно охарактеризовать как ситуацию принятия решения. Для задач принятия решений существенными являются следующие общие элементы:
1. Множества переменных и параметров. В их число входят:
Множество разрешающих или эндогенных переменных, значения которых рассчитываются лицом, принимающим решение.
Множество внешних или экзогенных переменных, значения которых не контролируются лицом, принимающим решение.
Множество параметров, которые так же контролируется и считаются в условиях задачи вполне определенными.
Модель-множество соотношений, связывающих все переменные и параметры.
Целевая функция-функция, функций, значение которой зависит от значений эндогенных переменных. Эта функция. Позволяет лицу, принимающему решения оценивать варианты.
Численные методы-методы, с помощью, которых можно систематически оценивать результаты различных решений.
Получение решения на модели, в конечном итоге, сводится к математической задаче нахождения некоторых вещественных значений эндогенных переменных, которые оптимизируют целевую функцию.
Если до недавнего времени все четыре перечисленные выше элемента ложились на лицо принимающее решение, то теперь умение пользоваться встроенными функциями EXCEL снимает наиболее утомительный пункт, а именно, применения численных методов, и делает исследование задач принятия решения более эффективными, так как теперь для решения одной и той же более эффективными, так как теперь для решения одной и той же задачи можно быстро просмотреть различного вида постановки в том числе и отличающиеся друг от друга по структуре.
3.2Безусловный экстремум
Excel обладает мощным встроенным средством для нахождения экстремальных значений функции одной или нескольких переменных. Для одно-экстремальных функций можно найти безусловный глобальный экстремум. Для многоэкстремальных функций можно найти условный локальный экстремум. Забегая вперед отметим, что для многоэкстремальных функций определить какой из локальных экстремумов будет найден невозможно без построения графика функции на интересующем нас интервале, так как численные методы нахождения экстремума ориентированы на поиск ближайшего решения к точке начального приближения и вообще говоря, требуют унимодальности функции.
Посмотрим различные примеры поиска экстремальных значений функции.
Задание6
Найти минимум и максимум функции на интервале, построить график.
2. 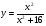
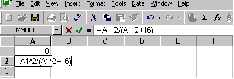
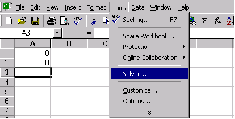
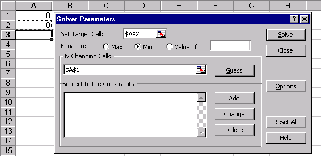
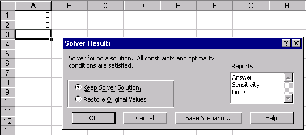
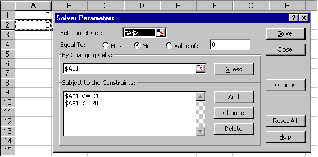
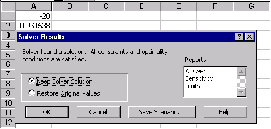
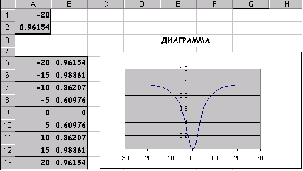
Рис.19
Для поиска безусловного экстремума функции сформируем лист электронной таблицы, как показано на рисунке 20. Функцию (6) запишем в клетку А2 где вместо переменной х следует указать адрес ячейки А1, которая содержит начальное приближение экстремума равное, например 0.
Для поиска минимума следует выполнить следующую последовательность действий:
1.Выполнить команду Сервис/Поиск решения…(получим лист электронной таблицы, как показано на рис.20).
2.Заполнить диалоговое окно Поиск решения… рис21
2.1.Щелкнуть левой клавишей мыши в поле. Установить целевую ячейку и щелкнуть на ячейке с формулой, в нашем случае это ячейка А2, абсолютный адрес которой. $А$2 появится в поле.
2.2. Выбрать поле Минимальное значение.
2.3. В поле. Изменяя ячейки ввести адреса ячеек, значения которых будут варьироваться в процессе поиска решения. В нашем случае это клеикаА1, абсолютный адрес которой. $А$1.
После выполнения пунктов 1-2 лист электронной таблицы будет выглядеть так, как показано на рис 21.
После щелчка на кнопке Выполнить получим решение поставленной задачи. В клетке А1 находится значение переменной Х равное 0.769231 при котором функция (5 ) достигает минимального значения равного –167,692. Рис22
Условный экстремум
Для функции одной переменной поиск экстремума возможен как на всей числовой оси, так и на некотором интервале, поиск на интервале уже можно считать поиском условного экстремума функции, т.к появляются ограничения на изменение значений аргумента.
На рис.21 в диалогом окне Поиск решения есть поле Ограничения м соответствующие ему команды: Добавить, Заменить, Удалить.
Рассмотрим предыдущую задачу, добавив условие поиска минимального значения на интервале [1;5]. Тогда диалоговое окно Поиск решения… следует видоизменить, добавив ограничения:
Щелкнув левой клавишей мыши в поле Ограничения и затем на кнопке Добавить , откроем диалоговое окно Добавление ограничения. Рис23,,,.. которое следует заполнить так как показано на рисунке.
После добавления последнего ограничения диалоговое окно Поиск решения…будет содержать математическую постановку задачи экстремума и выглядит след.образом.
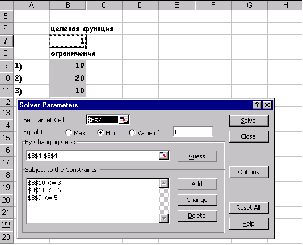
После щелчка на кнопке Выполнить получим следующее решение:
У=-167 при х=1, отличающееся от решения, полученного в предыдущем случае. Здесь в качестве минимального значения выступает наименьшее значение функции на интервале[1;5], совпадающее с левой границей интервала.
Все численные методы нахождения оптимальных значений для корректной работы требуют ,чтобы функция на интервале была унимодальной.
При такой постановке задачи значения труда и капитала определяется как 5 и 2 единицы соответственно. Получающиеся значение целевой функции при этом равно 3.37. Теперь можно построить график, на котором отражены линия безразличия использования труда и капитала при выпуске 3.37 и линия ограничения на средства, предназначенные для расходов на труд и капитал.
Полученные кривые касаются в найденной точке, что согласуется с теорией фирмы. Рис 31
Максимизация выпуска при ограничениях на средства
3.4 Математическое программирование
Различные методы оптимального управления, получившие заметное развитие во второй половине двадцатого века, благодаря созданию и распространению компьютерной техники, не только отвечают насущным потребностям экономической науки, но и начинают играть роль важнейшего ее составного элемента. И это вполне естественно, поскольку одной из главных задач экономической науки является разработка теоретического фундамента управления, т.е. методов наилучшего распределения ограниченных ресурсов (людских, материально -вещественных, финансовых, временных) для поддержания функционирования и развития предприятия или экономики страны.
Однако, чтобы обнаружить глубинную связь между математическим программированием и экономической наукой, понадобились усилия многих ученых.
Анализируя возможности Поиска решения … можно заметить, что он применим для решения достаточно широкого класса задач математического программирования.
Если задачу принятия решений в области управления можно сформулировать в виде подчиненных m произвольным ограничениям.
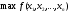 при
при
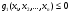
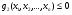
……………………
gm(x1,x2,…,xn)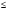 0
0
то Поиск решения… позволяет найти решение такой задачи, которая в формальной постановке может быть задачей:
линейного программирования
нелинейного программирования
целочисленного программирования
частично целочисленного программирования
Кроме того у лиц, принимающего решения есть возможность изменить параметры работы Поиска решения…, повышающие эффективность поиска оптимального решения. Рис.32
3.4.1. Линейное программирование
 Найти минимум функции F=5x1+x2
Найти минимум функции F=5x1+x2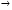 min
min
 при ограничениях:
при ограничениях:
 3x1+4x2
3x1+4x2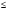 12
12
 -2x1+x2
-2x1+x2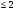
 x1-2x2
x1-2x2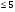
 x1+x2
x1+x2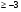 x1,x2 – произвольные
x1,x2 – произвольные
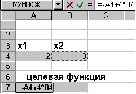
Сформируем страницу электронной таблицы и постановку задачи линейного программирования в диалоговом окне Поиска решения…
После выполнения поставленной задачи получаем следующее значение переменных
Как видим, при найденных значениях x1,x2 целевая функция принимает минимальное значение, равное –9.66 и этим удовлетворяются все ограничения поставленной задачи.
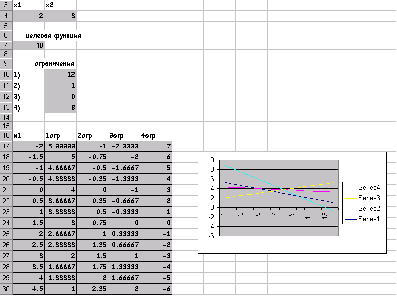
Графическое решение поставленной задачи выглядит так:
Задание 7
Решить задачу линейного программирования с помощью Поиска решения…, показать графически область допустимых решений и целевую функцию.
2.F=-x1+4x2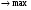
при
3x1+2x2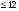
2x1-x2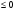
-3x1+2x2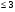
x1+2x2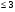
x1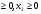

Задание 8
По описанию задачи сделать математическую постановку, решить.создать отчет и прокомментировать его.
№2
Фирма изготовляет два типа электрических выключателей, типа А, доход от которых равен 0.4$. На каждый выключатель и типа В – доход от которых равен 0.3$. На изготовление выключателя А требуется в три раза больше рабочего времени, чем на изготовления типа В.
Если бы изготавливались выключатели только типа В, то дневного рабочего времени хватило бы для изготовления ровно 1000 выключателей. Поставка медного провода обеспечивает изготовление только 800 выключателей в день (любого типа). Для выключателей требуются специальные изоляторы, их можно получить в день для типа А не более 400, для типа В не более 700. Задача состоит в максимизации дохода при всех указанных выше ограничениях.
Задание 9
Составить задачу двойственную к данной задаче линейного программирования и решить обе с помощью Поиска решения…
2.F=-x1+x2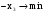
при
x1+2x2 –x3 5 
2x2+x43
x3+2x46
xj0.j=1.4
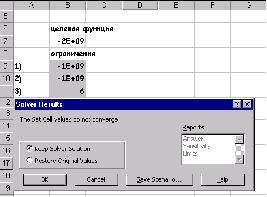
Задание 12
С помощью Поиска решения… найти решение системы нелинейных алгебраических уравнений. Исследовать зависимость получаемого решения от различных начальных приближений(менее трёх), оформить исследования в виде таблицы.
№2
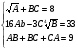


ЛИТЕРАТУРА:
EXCEL5.0 Для профессионалов. М-1995
EXCEL7.0 М-1997
А.А.Горчаков, И.В.Орлов. Компьютерные экономико-математические модели. М-1995
И.Л.Акулич. Математическое программирование а в примерах и задачах. М-1986
М.Кубонива. Математическая экономика на персональном компьютере. М-1991.

Нравится материал? Поддержи автора!
Ещё документы из категории история:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ