Экзаменационные вопросы и билеты по линейной алгебре за весенний семестр 2001 года
примерный перечень экзаменационных вопросов
линейная алгебра
Прямоугольная матрица, ее порядок, главная и побочная диагонали. Единичная, нулевая, треугольная, симметричная, транспонированная матрицы. Примеры.
Сложение матриц, умножение матрицы на число, умножение матриц. Свойства ассоциативности и коммутативности матриц. Примеры.
Приведение матриц к ступенчатому виду методом Гаусса. Элементарные преобразования над строками матрицы. Пример. Ранг матрицы.
Система из “m” линейных уравнений с “n” неизвестными. Векторно-матричная форма записи. Расширенная матрица системы. Пример.
Однородные и неоднородные системы уравнений. В каком случае они имеют единственное решение? Пример.
Решение однородной и неоднородной систем методом Гаусса. Пример.
Однородные системы и их свойства. Эквивалентные системы.
Свободные и несвободные переменные однородной системы. Частное и общее решение. Пример.
Совместные системы уравнений. Теорема Кронекера-Капелли. Пример.
Вектор решения линейной системы уравнений. Общее и частное решение неоднородной системы уравнений. Основные свойства решений.
Модель Леонтьева межотраслевого баланса. Ее математическая модель.
Определитель матрицы. Его порядок. Понятие определителя применительно к матрицам второго и третьего порядков. Алгебраическое дополнение элемента. Разложение определителя по строке или столбцу.
Сформулировать свойства определителя.
Какую матрицу называют обратной? Условие ее существования.
Вычисление определителя с использованием метода Гаусса.
Построение обратной матрицы с использованием алгебраических дополнений и методом Гаусса.
Даны матрицы А=
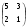 и В=
и В=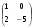 . Найти АВ - ВА.
. Найти АВ - ВА.Найти ранг матрицы:
 A =
A = .
.Найти ранг матрицы

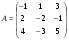 .
.Исследовать сколько решений может иметь система уравнений:
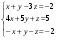 .
.Найти общее решение однородной системы:
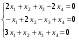 .
.Исследовать и решить в случае совместности систему уравнений:
 .
.Вычислить определитель матрицы det A, где А =
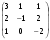 методом Гаусса.
методом Гаусса.Что называется линейным пространством? Элемент линейного пространства. Какое множество функций на отрезке [a, b] образует пространство C[a, b]?
Свойства коммутативности и ассоциативности сложения векторов.
Арифметическое пространство Rn. Что называют компонентами вектора?
Определите понятие подпространства Н в пространстве V. Приведите примеры линейных подпространств в линейном пространстве V, в пространстве Rn.
Определите понятие линейной комбинации векторов u и v линейного пространства. Какая система векторов называется линейно независимой?
Запишите свойства линейно зависимой системы векторов и линейно независимой системы векторов.
Приведите примеры линейно независимых векторов и функций в линейном пространстве.
Базис линейного пространства, разложение вектора по базису, координаты вектора u в базисе е1, е2 … еn. Примеры стандартных базисов в прстранстве Rn.
Размерность линейного пространства. Линейная оболочка системы векторов. Размерность линейного подпространства W линейного пространства V.
Линейные операции над свободными векторами в координатной форме в произвольном линейном пространстве.
Как определяется матрица перехода от старого базиса b к новому c?
Какими свойствами обладает матрица перехода от старого базиса b к новому c?
Сформулируйте теорему о разложении любого вектора линейного пространства по базису.
Запишите формулы преобразования координат вектора x линейного пространства L при переходе от старого базиса b к новому c.
Как определяется скалярное произведение двух векторов? Какое пространство называется евклидовым? Неравенство Коши-Буняковского.
Ортогональные векторы линейного пространства.
Понятие нормы вектора. Каким аксиомам подчиняется норма вектора?
Ортогональная система векторов. Является ли она линейно зависимой?
Понятие ортогонального и ортонормированного базисов линейного пространства.
Какую матрицу называют матрицей Грама и как вычисляются ее элементы?
Что называется процессом ортогонализации?
Сформулируйте необходимое и достаточное условие линейной зависимости векторов.
Составьте матрицу Грама для системы векторов е1=(1, -1, 2), е2=(1, 1, 1), е3=(1, 0, 1) трехмерного пространства.
Докажите, что для любых двух векторов а и с векторное уравнение a + x = c относительно x имеет решение, и при этом единственное.
Запишите матрицу перехода от базиса b к новому с, если b1=-2с1-3с2-2с3, b2=7с1+8с2+9с3, b3=3с1+4с2+5с3.
Выясните, образует ли линейное пространство множество всех векторов данной плоскости, не параллельных данной прямой, если в качестве операций взяты операции сложения векторов и умножения вектора на число.
Выясните, образует ли множество функций вида а cos t +b sin t, t (-,), a,b R, линейное пространство относительно обычных операций сложения функций и умножения функции на число.
Образует ли линейное пространство множество многочленов степени n относительно обычных операций сложения многочленов и умножения многочлена на число?
Образует ли линейное пространство множество функций, непрерывных на отрезке [a,b], относительно операций сложения функций и умножения функции на число?
Докажите, что множество матриц-столбцов высоты n образует линейное пространство относительно матричных операций сложения и умножения на число.
Докажите, что dim V2 = 2, dim V3 = 3.
Не проводя вычислений, выясните, является ли система векторов а1=(-4, 2, 3), а2= (-3, 5, 1), а3 = (1,-7, 3), а4= (12,-5,4) линейно независимой?
Выясните, образуют ли векторы а1=(1, 0, 0, 0), а2= (1, 1, 0, 0), а3 = (1,1, 1, 0), а4= (1,1,1, 1) базис в линейном арифметическом пространстве R4?
Может ли матрица А =
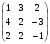 быть матрицей перехода от одного базиса трехмерного пространства к другому?
быть матрицей перехода от одного базиса трехмерного пространства к другому?Какой вид имеет матрица перехода от старого базиса к новому, если матрица перехода от нового базиса к старому является треугольной? Симметрической?
Для каких векторов евклидова пространства неравенство Коши-Буняковского превращается в равенство?
Дайте понятие линейного оператора, действующего в линейном пространстве L. Приведите примеры.
Какая матрица называется матрицей линейного оператора?
Какую матрицу имеет нулевой оператор, действующий в пространстве L? Какой вид у матрицы тождественного оператора, действующего в пространстве L?
Сформулируйте теорему о связи координат вектора-прообраза с координатами вектора-образа оператора А, действующего в пространстве L?
В каком случае совпадают матрицы двух различных линейных операторов?
Какое соответствие существует между квадратными матрицами порядка n и линейными операторами, действующими в n-мерном линейном пространстве?
Напишите зависимость, связывающую матрицы Аb и Ае в различных базисах b и e линейного пространства.
Определение характеристического уравнения матрицы А.
Дайте определение понятия собственное число линейного оператора А. Какой вектор называется собственным вектором оператора? Как его найти?
Что означает понятие «собственное подпространство», отвечающее данному собственному значению?
Составьте характеристическое уравнение для оператора А, если его матрица А=
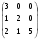 . Найдите собственные значения и собственные векторы линейного оператора А.
. Найдите собственные значения и собственные векторы линейного оператора А.Скольким собственным значениям может соответствовать один и тот же собственный вектор?
Известно, что собственные значения 1, 2,..,n линейного оператора попарно различны. Что можно сказать о линейной зависимости соответствующей им системы собственных векторов?
Известно, что базис е состоит из собственных векторов оператора А. Что можно сказать о матрице оператора в этом базисе?
Когда матрица оператора А подобна некоторой диагональной?
Пусть 1, 2,.., n - собственные значения оператора А. Найдите собственные значения линейного оператора, матрицей которого является матрица А2, А-1.
Дайте определение оператора, сопряженного к данному линейному оператору А. Сколько сопряженных операторов может быть у оператора А в евклидовом пространстве?
Какая матрица является матрицей оператора сопряженного линейному оператору А с матрицей А в ортонормированном базисе?
Дайте определение самосопряженного оператора. Приведите пример самосопряженного оператора.
Какова матрица самосопряженного оператора в ортонормированном базисе?
Что можно сказать об операторе А, если известно, что его матрица в некотором ортонормированном базисе является симметрической?
Каковы корни характеристического уравнения самосопряженного оператора?
Сколько собственных значений имеет симметрическая матрица порядка n?
Каким свойством обладают собственные векторы самосопряженного оператора?
Когда в евклидовом пространстве существует ортонормированный базис, в котором матрица линейного оператора имеет диагональный вид?
Докажите, что (А+ В)* = А* + В* и (АВ)* = В* А*.
В ортонормированном базисе оператор А имеет матрицу А =
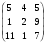 . Найдите матрицу сопряженного ему оператора в этом же базисе.
. Найдите матрицу сопряженного ему оператора в этом же базисе.Какая матрица называется ортогональной матрицей и чему равен ее определитель?
Свойства ортогональных матриц.
Что такое квадратичная форма? Дайте понятие матрицы квадратичной формы.
Запишите квадратичную форму в координатах в некотором базисе.
Что такое канонический вид квадратичной формы? Найти ее для x2 + xy + y2.
Какая квадратичная форма называется положительно определенной? Неотрицательно определенной?
Сформулируйте критерий Сильвестра.
Запишите закон инерции для квадратичной формы.
Что представляет собой метод итераций?
Дайте определение Гессиана.
Составьте Гессиан для функции f ( x1,....,xn )= x12 +x 1 x 2+ .... + x 1x n .
Приведите квадратичную форму х12 - 4х1х2 к каноническому виду методом выделения квадратов.
Какую квадратичную форму можно привести к каноническому виду?
Как изменяется характеристическое уравнение матрицы при ортогональном преобразовании квадратичной формы?
Выясните, является ли квадратичная форма с матрицей А =
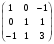 положительно определенной?
положительно определенной?Когда диагональные элементы симметрической матрицы ― положительные числа?
Найдите ранг квадратичной формы трех переменных 2ху + 2уz +2хz.
Какой ранг может иметь положительно определенная форма от n переменных?
Запишите матрицу перехода от базиса е к базису е, если е1= е1+ е2+7е3, е2=(7/6) е1- е2, е3=- е1+ е2+ е3.
Является ли линейным преобразование Ах = (6х1 - 5х2,-2х2, х3 - х1)?
Чему равно скалярное произведение векторов в арифметическом пространстве Rn?
Что можно сказать о собственных векторах, если они соответствуют различным собственным значениям?
Определите, каким является базис а=(1/
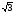 , 1/
, 1/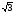 ,1/
,1/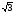 ), b=(1/
), b=(1/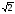 , -1/
, -1/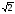 , 0), с =(1/
, 0), с =(1/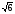 , 1/
, 1/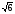 ,-2/
,-2/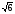 ).
).Нормируйте вектор х = 3i + 4j + 5k + 7m.
Экзаменационный билет по предмету
ЛИНЕЙНАЯ АЛГЕБРА
Билет № 1
Описать модель Леонтьева межотраслевого баланса.
Найти общее решение однородной системы:
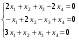 .
.Как записывается свойство ассоциативности сложения векторов?
Когда в евклидовом пространстве существует ортонормированный базис, в котором матрица линейного оператора имеет диагональный вид?
В ортонормированном базисе оператор А имеет матрицу А =
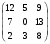 . Найдите матрицу сопряженного ему оператора в этом же базисе.
. Найдите матрицу сопряженного ему оператора в этом же базисе.
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
ЛИНЕЙНАЯ АЛГЕБРА
Билет № 2
Какие прямоугольные матрицы можно привести к ступенчатому виду? Метод приведения матрицы к ступенчатому виду. Пример.
Найти матрицу
 А-1, обратную к матрице А и с ее помощью решить систему А
А-1, обратную к матрице А и с ее помощью решить систему А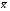 =
= 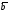 , где А =
, где А = 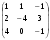 ,
, 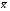 =
= 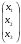 ,
, 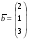 .
.Образует ли линейное пространство множество многочленов степени n относительно обычных операций сложения многочленов и умножения многочлена на число?
Какая матрица называется ортогональной матрицей?
Запишите матрицу перехода от базиса b к новому с, если b1=3с1-с2+2с3 , b2=-6с1+5с2 -2с3, b3=4с1+с2-с3.
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
ЛИНЕЙНАЯ АЛГЕБРА
Билет № 3
Дать определение системы из «m» линейных уравнений с «n» неизвестными. Векторно-матричная форма записи системы линейных уравнений.
Исследовать и решить в случае совместности систему уравнений:
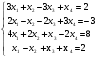 .
.Дайте определение понятия арифметического пространства Rn.
Какой матрицей является матрица, транспонированная к ортогональной?
Докажите, что для любых двух векторов а и с векторное уравнение а+х = с относительно х имеет решение, и притом единственное.
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
ЛИНЕЙНАЯ АЛГЕБРА
Билет № 4
Какой метод используется при решении системы линейных уравнений (на примере)?
Исследовать и решить в случае совместности систему уравнений:
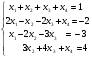 .
.Запишите свойства линейно зависимой системы векторов.
Дайте определение Гессиана.
Составьте Гессиан для функции f ( x1,....,xn )= x12 +x 1 x 2+ .... + x 1x n .
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
ЛИНЕЙНАЯ АЛГЕБРА
Билет № 5
Неоднородные системы уравнений. Основные свойства решений.
Найти матрицу
 А-1, обратную к матрице А и с ее помощью решить систему А
А-1, обратную к матрице А и с ее помощью решить систему А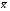 =
= 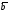 , где А =
, где А = 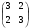 ,
,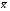 =
=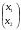 ,
, 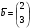 .
.Сформулируйте теорему о связи координат вектора-прообраза с координатами вектора-образа оператора А, действующего в пространстве L .
Какая матрица является матрицей оператора сопряженного линейному оператору А с матрицей А в ортонормированном базисе?
Выясните, является ли квадратичная форма с матрицей А =
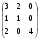 положительно определенной.
положительно определенной.
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
ЛИНЕЙНАЯ АЛГЕБРА
Билет № 6
Правило построения обратной матрицы на примере матрицы 2-го порядка с использованием алгебраических дополнений.
Совместна ли система уравнений:
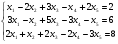 ?
?Выясните, образует ли линейное пространство множество всех векторов данной плоскости, не параллельных данной прямой, если в качестве операций взяты операции сложения векторов и умножения вектора на число.
Скольким собственным значениям может соответствовать один и тот же собственный вектор?
Составьте Гессиан для функции f ( x1,....,xn )= x12 + 2x22+ .... + nxn2 .
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
ЛИНЕЙНАЯ АЛГЕБРА
Билет № 7
Что называют определителем матрицы. Порядок определителя. Понятие определителя применительно к матрице второго порядка. Пример.
Найти ранг матрицы

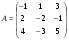 .
.Как записывается свойство коммутативности сложения векторов?
Какую квадратичную форму можно привести к каноническому виду?
Найдите ранг квадратичной формы трех переменных х2 + у 2 +2хz.
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
ЛИНЕЙНАЯ АЛГЕБРА
Билет № 8
Подчиняется ли умножение матриц свойству ассоциативности и перестановки сомножителей? Привести пример некоммунитативных матриц. Пример перестановочных матриц.
Найти общее решение однородной системы:
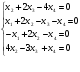 .
.Что называется линейным пространством?
Чему равен определитель ортогональной матрицы?
В ортонормированном базисе оператор А имеет матрицу А =
 . Найдите матрицу сопряженного ему оператора в этом же базисе.
. Найдите матрицу сопряженного ему оператора в этом же базисе.
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
ЛИНЕЙНАЯ АЛГЕБРА
Билет № 9
Дать определение ранга матрицы. Пример.
Убедиться, что система
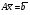 имеет единственное решение, и найти это решение методом Гаусса:
имеет единственное решение, и найти это решение методом Гаусса: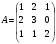 ,
, 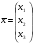 ,
, 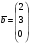 .
.Какая система векторов называется линейно независимой?
Какой матрицей будет матрица, обратная к ортогональной?
Докажите, что (А+ В)* = А* + В*.
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
ЛИНЕЙНАЯ АЛГЕБРА
Билет № 10
Какие преобразования можно выполнить над строками матрицы? Пример.
Найти общее решение однородной системы уравнений
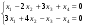 .
.Какой базис линейного пространства называется ортогональным?
Сколько сопряженных операторов может быть у оператора А в евклидовом пространстве?
Чему равно скалярное произведение векторов в арифметическом пространстве Rn?
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
ЛИНЕЙНАЯ АЛГЕБРА
Билет № 11
При решении однородной системы какие переменные называют свободными, а какие несвободными? Чему равно число свободных переменных?
Исследовать и решить в случае совместности систему уравнений:
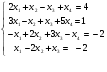 .
.Докажите, что множество матриц-столбцов высоты n образует линейное пространство относительно матричных операций сложения и умножения на число.
Сколько собственных значений имеет симметрическая матрица порядка n?
Запишите матрицу перехода от базиса b к новому с, если b1=-2с1-3с2-2с3, b2=7с1+8с2+9с3, b3=3с1+4с2+5с3.
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
ЛИНЕЙНАЯ АЛГЕБРА
Билет № 12
Элементарные преобразования над строками матрицы. Пример.
Убедиться, что система
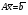 , имеет единственное решение, и найти это решение методом Гаусса:
, имеет единственное решение, и найти это решение методом Гаусса: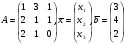 .
.Для каких векторов евклидова пространства неравенство Коши – Буняковского превращается в равенство?
Чему равна матрица, обратная к ортогональной?
Найдите ранг квадратичной формы трех переменных 2ху + 2уz +2хz.
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
ЛИНЕЙНАЯ АЛГЕБРА
Билет № 13
Решение однородной системы методом Гаусса. Пример.
Найти матрицу
 А-1, обратную к матрице А и с ее помощью решить систему А
А-1, обратную к матрице А и с ее помощью решить систему А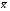 =
= 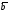 , где А =
, где А = 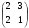 ,
,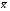 =
=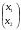 ,
, 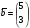 .
.Определите понятие подпространства Н в пространстве V.
Дайте понятие матрицы квадратичной формы.
Какой нормированный вектор соответствует вектору х = -5i + 3j + 7k?
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
ЛИНЕЙНАЯ АЛГЕБРА
Билет № 14
Какую систему уравнений называют неоднородной? В каком случае она имеет единственное решение?
Найти матрицу А-1, обратную к матрице
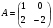 .
.Что называется разложением вектора по базису?
Когда диагональные элементы симметрической матрицы ― положительные числа?
Докажите, что (АВ)* = В* А*.
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
ЛИНЕЙНАЯ АЛГЕБРА
Билет № 15
Какую систему уравнений называют однородной? В каком случае она имеет единственное решение?
Сколько решений может иметь система уравнений:
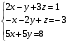 ?
?Что называют координатами вектора u в базисе е1, е2 ... еn.
Запишите закон инерции для квадратичной формы.
В ортонормированном базисе оператор А имеет матрицу А =
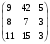 . Найдите матрицу сопряженного ему оператора в этом же базисе.
. Найдите матрицу сопряженного ему оператора в этом же базисе.
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
ЛИНЕЙНАЯ АЛГЕБРА
Билет № 16
Сформулировать теорему Кронекера-Капелли. Проиллюстрировать ее примером.
Вычислить определитель матрицы det A, где А =
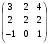 методом Гаусса.
методом Гаусса.Определите понятие линейной комбинации векторов u и v линейного пространства.
Каким свойством обладают собственные векторы самосопряженного оператора?
Выясните, образует ли множество функций вида а cos t +b sin t, t (-,), a,b R, линейное пространство относительно обычных операций сложения функций и умножения функции на число.
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
ЛИНЕЙНАЯ АЛГЕБРА
Билет № 17
Решение неоднородной системы методом Гаусса (на примере).
Совместна ли следующая система:
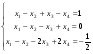 ? Найти ее решение.
? Найти ее решение.Дайте определение размерности линейного подпространства W линейного пространства V.
Какой многочлен называется характеристическим многочленом матрицы?
Является ли линейным преобразование Ах = (6х1 - 5х2,-2х2, х3 - х1)?
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
ЛИНЕЙНАЯ АЛГЕБРА
Билет № 18
Какие матрицы называют равными? Сложение матриц. Пример. Умножение матрицы на число. Пример.
Сколько линейно независимых решений имеет система:
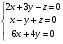 ?
?Какие векторы линейного пространства называются ортогональными?
Что такое канонический вид квадратичной формы?
Докажите, что dim V2 = 2, dim V3 = 3.
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
ЛИНЕЙНАЯ АЛГЕБРА
Билет № 19
В чем заключается прямой и обратный ход метода Гаусса при решении системы уравнений (на примере)?
Существует ли матрица А-1, обратная
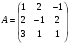 ?
?Как определяется матрица перехода от старого базиса b к новому с?
Какая матрица называется симметрической?
Составьте Гессиан для функции f ( x1,....,xn) = x12 + x 2+ .... + x n-1+xn2 .
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
ЛИНЕЙНАЯ АЛГЕБРА
Билет № 20
Какие системы линейных уравнений называют совместными? В каком случае система является несовместной?
Совместна ли система уравнений:
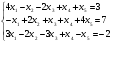 ? Найти ее решение.
? Найти ее решение.Как называется элемент линейного пространства?
Известно, что базис е состоит из собственных векторов оператора А. Что можно сказать о матрице оператора в этом базисе?
Запишите матрицу перехода от базиса b к новому с, если b1=-с1-7с2+2с3, b2=-9с1+ 8с2-с3, b3=с1+2с2+5с3.
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
ЛИНЕЙНАЯ АЛГЕБРА
Билет № 21
Какое решение неоднородной системы линейных уравнений называют общим? Какое – частным?
Сколько решений может иметь система уравнений:
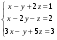 ?
?Запишите свойства линейно независимой системы векторов.
Что можно сказать об операторе А, если известно, что его матрица в некотором ортонормированном базисе является симметрической?
Что можно сказать о собственных векторах, если они соответствуют различным собственным значениям?
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
ЛИНЕЙНАЯ АЛГЕБРА
Билет № 22
Построение обратной матрицы с использованием метода Гаусса (на примере).
Вычислить определитель матрицы det A, где А =
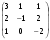 методом Гаусса.
методом Гаусса.В каком случае совпадают матрицы двух различных линейных операторов?
В каком базисе матрица линейного оператора А является диагональной?
Является ли линейно зависимой система векторов а=(5,4,3), b=(3,3,2), с=(8,1,3)?
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
ЛИНЕЙНАЯ АЛГЕБРА
Билет № 23
Основные свойства определителя.
Сколько решений может иметь система уравнений:
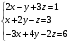 ?
?Какой вид имеет матрица перехода от старого базиса к новому, если матрица перехода от нового базиса к старому является треугольной?
Запишите квадратичную форму в координатах в некотором базисе.
Может ли матрица А =
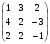 быть матрицей перехода от одного базиса трехмерного пространства к другому?
быть матрицей перехода от одного базиса трехмерного пространства к другому?
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
ЛИНЕЙНАЯ АЛГЕБРА
Билет № 24
Чему равен определитель треугольной матрицы? Меняют ли элементарные преобразования величину определителя? В каком случае определитель матрицы не равен нулю?
Исследовать и решить в случае совместности систему уравнений:
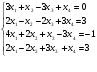 .
.Запишите формулы преобразования координат вектора х линейного пространства L при переходе от старого базиса b к новому с.
Какова матрица самосопряженного оператора в ортонормированном базисе?
Запишите матрицу перехода от базиса b к новому с, если b1= 4с1-5с2 +с3, b2=с1-3с2-2с3, b3=5с1+с2+с3.
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
ЛИНЕЙНАЯ АЛГЕБРА
Билет № 25
Какое решение однородной системы уравнений называют общим, частным? Пример.
Найти матрицу
 А-1, обратную к матрице А и с ее помощью решить систему А
А-1, обратную к матрице А и с ее помощью решить систему А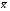 =
= 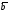 , где А =
, где А = 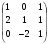 ,
, 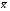 =
= 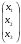 ,
, 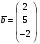 .
.Какое множество функций на отрезке [a,b] образует пространство С[a,b] ?
Дайте определение понятия собственного числа линейного оператора А.
Определите, каким является базис а=(1/
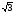 , 1/
, 1/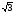 ,1/
,1/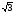 ), b=(1/
), b=(1/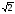 , -1/
, -1/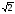 , 0), с =(1/
, 0), с =(1/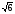 , 1/
, 1/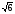 ,-2/
,-2/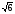 ).
).
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
ЛИНЕЙНАЯ АЛГЕБРА
Билет № 26
Приведение матрицы к ступенчатому виду методом Гаусса. Пример.
Вычислить определитель матрицы det A, где А =
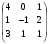 методом Гаусса.
методом Гаусса.Образует ли линейное пространство множество функций, непрерывных на отрезке [a,b], относительно операций сложения функций и умножения функции на число?
Какая квадратичная форма называется неотрицательно определенной?
Найдите ранг квадратичной формы трех переменных х2 + 2ху +z2.
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
ЛИНЕЙНАЯ АЛГЕБРА
Билет № 27
Какой вектор называют решением линейной системы уравнений? Что значит решить систему линейных уравнений? Какие системы называют эквивалентными?
Найти матрицу
 А-1, обратную к матрице А и с ее помощью решить систему А
А-1, обратную к матрице А и с ее помощью решить систему А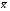 =
= 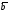 , где А =
, где А = 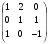 ,
, 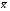 =
= 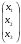 ,
, 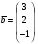 .
.Дайте определение размерности линейного пространства.
При каком условии существует базис, в котором матрица линейного оператора является диагональной?
В ортонормированном базисе оператор А имеет матрицу А =
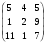 . Найдите матрицу сопряженного ему оператора в этом же базисе.
. Найдите матрицу сопряженного ему оператора в этом же базисе.
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
ЛИНЕЙНАЯ АЛГЕБРА
Билет № 28
Какую матрицу называют невырожденной? При каком значении определителя строки матрицы являются зависимыми, а при каком – независимыми?
Найти ранг матрицы: A =
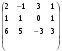 .
.Сформулируйте необходимое и достаточное условие линейной зависимости векторов.
Какой вектор называется собственным вектором оператора?
Составьте характеристическое уравнение для оператора А, если его матрица А=
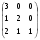 . Найдите собственные значения оператора А.
. Найдите собственные значения оператора А.
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
ЛИНЕЙНАЯ АЛГЕБРА
Билет № 29
Какую матрицу называют матрицей системы уравнений? Какая матрица называется расширенной матрицей системы? Как записываются вектор неизвестных и вектор правых частей уравнений?
Сколько решений может иметь система уравнений:
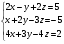 ?
?Напишите зависимость, связывающую матрицы Аb и Ае в различных базисах b и e линейного пространства.
Сколько собственных значений имеет самосопряженный оператор, действующий в n-мерном евклидовом пространстве?
Не проводя вычислений, выясните, является ли система векторов а1=(-4, 2, 3), а2= (-3, 5, 1), а3 = (1,-7, 3), а4= (12,-5,4) линейно независимой.
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
ЛИНЕЙНАЯ АЛГЕБРА
Билет № 30
Какую матрицу называют единичной, нулевой, треугольной? Пример.
Сколько решений может иметь система уравнений:
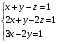 ?
?Какой вид у матрицы тождественного оператора, действующего в пространстве L?
Дайте определение оператора, сопряженного к данному линейному оператору А.
Запишите матрицу перехода от базиса b к новому с, если b1=с1-3с2+2с3, b2=-2с1+с2 - с3, b3=с1+2с2-2с3.
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
ЛИНЕЙНАЯ АЛГЕБРА
Билет № 31
Как записывается формула разложения определителя по строке или столбцу? Пример.
Найти матрицу
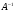 , обратную к матрице А и с ее помощью решить систему
, обратную к матрице А и с ее помощью решить систему 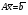 , где
, где 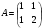 ,
, 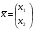 ,
, 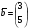 .
.Запишите неравенство Коши - Буняковского.
Дайте определение самосопряженного оператора.
Приведите квадратичную форму х12 + 4х1х2 + x2x3 + x32 к каноническому виду методом выделения квадратов.
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
ЛИНЕЙНАЯ АЛГЕБРА
Билет № 32
Неоднородная система линейных уравнений. Ее общее и частное решения. Пример.
Найти ранг матрицы:
 A =
A = .
.Дайте понятие ортонормированного базиса линейного пространства.
Как находятся собственные векторы линейного оператора?
Пусть 1, 2,.., n - собственные значения оператора А. Найдите собственные значения линейного оператора, матрицей которого является матрица А2.
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
ЛИНЕЙНАЯ АЛГЕБРА
Билет № 33
Однородные системы уравнений и их основные свойства.
Сколько решений может иметь система уравнений:
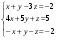 ?
?Каким аксиомам подчиняется норма вектора?
Какая квадратичная форма называется положительно определенной?
Запишите матрицу перехода от базиса b к новому с, если b1= 4с1- с2+9с3, b2 =-с1+6с2-11с3, b3=5с1+3с2-2с3.
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
ЛИНЕЙНАЯ АЛГЕБРА
Билет № 34
Понятие «определитель» применительно к матрице третьего порядка. Какую величину называют алгебраическим дополнением элемента? Пример.
Даны матрицы
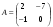 и
и 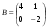 . Найти АВ-ВА.
. Найти АВ-ВА.Какое пространство называется евклидовым?
Когда матрица оператора А подобна некоторой диагональной?
Выясните, образуют ли векторы а1=(1, 0, 0, 0), а2= (1, 1, 0, 0), а3 = (1,1, 1, 0), а4= (1,1,1, 1) базис в линейном арифметическом пространстве R4.
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
ЛИНЕЙНАЯ АЛГЕБРА
Билет № 35
Задача межотраслевого баланса. Ее математическая модель.
Исследовать и решить в случае совместности систему уравнений:
 .
.Что означает запись dim V?
Что такое квадратичная форма?
Пусть 1, 2,.., n - собственные значения оператора А. Найдите собственные значения линейного оператора, матрицей которого является матрица А-1.
Зав. кафедрой
--------------------------------------------------

Нравится материал? Поддержи автора!
Ещё документы из категории история:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ