Математические основы теории систем









































 Саратовский Государственный Технический Университет
Саратовский Государственный Технический Университет
Балаковский Институт Техники Технологии и Управления
Кафедра:
Специальность:
Курсовая работа
МОТС
Выполнил:
Принял:
Балаково 2009г.
I-часть
Задание1: По виду электрической схемы построить математическую модель объекта управления в пространстве состояния.
Задание2: По построенной модели составить структурную схему и сигнальный граф.
Задание3: Используя формулу Мейсона найти передаточную функцию объекта управления.
Задание4: По передаточной функции объекта управления определить временные и частотные характеристики. Построить их зависимость: АЧХ, ФЧХ.
Задание5: По полученным зависимостям определить прямые и косвенные оценки качества объекта управления.
II-часть.
Задание1: По заданной корреляционной функции Kx() определить спектральную плотность Sx() для белого шума, который подается на вход формирующего фильтра.
Задание2: По заданным статистическим характеристикам Se,Sv определить передаточную функцию формирующего фильтра (р)
Задание3: Представить объект управления в виде
(p)
W(p)
V(t) X(t) Y(t)
и оценить качество полученной системы по переходной характеристике.
Задание4: Сделать вывод по работе.
I-часть
Данные
-
R1
R2
R3
R4
L1
L2
C2
I2
Ом
Гн.
10-6Ф
?
328
395
118
215
24
24
19605
L1 e(t) L2
Построить математическую модель объекта управления в пространстве состояния.
ОУ
В схеме три элемента, запасающих энергию: 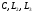 , следовательно, математическая модель должна быть третьего порядка.
, следовательно, математическая модель должна быть третьего порядка.
2. Построение математической модели.
Задаемся направлением контурных токов 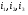 . Составляем три уравнения по второму закону Кирхгофа для контуров:
. Составляем три уравнения по второму закону Кирхгофа для контуров:
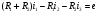 (1)
(1)
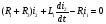 (2)
(2)
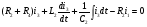 (3)
(3)
В уравнении (3) есть интеграл, поэтому дифференцируем его:
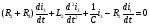 (3*)
(3*)
В уравнениях (3*), (2), (3) есть производные, в качестве 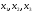 выбираем элементы с производными и производные берем на порядок ниже:
выбираем элементы с производными и производные берем на порядок ниже:
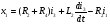 (4)
(4)
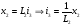 (5)
(5)
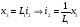 (6)
(6)
Запишем введенный вектор состояния в виде дифференциальных уравнений первого порядка.
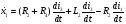
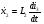
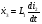
Уравнение в пространстве состояний записывается в левой части:
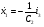
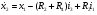
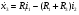
В полученных уравнениях имеется шесть переменных 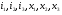 . Необходимо уйти от
. Необходимо уйти от 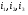 , выразив их через
, выразив их через 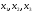
Из выражения (1) выразим 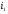 :
:
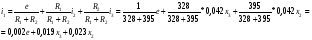
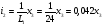
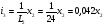
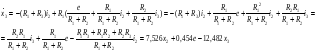
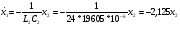
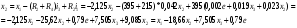
Получили три дифференциальных уравнения и одно уравнение для выходного параметра.
Запишем полученную систему уравнений в матричном виде:
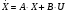
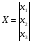

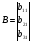
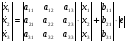
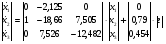
Получим матричное уравнение для выходной переменной:
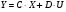
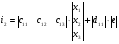
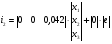
Построение сигнального графа.
Перепишем уравнения в общем, виде для построения графа системы:
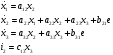
Построение графа произведем в два шага:
Шаг 1. Ставим точки входа, выхода системы 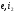 и векторы параметров
и векторы параметров
Шаг 2. Соединяем все параметры связями согласно системе уравнений.
с13
b21 a22
a33
1/p a23 1/p b31
e X 3 X 3 X 2 X 2 i2
a32
a21
1/p a12
X 1 X 1
Нахождение передаточной функции по формуле Мейсона.
k-количество возможных путей от входа к выходу
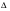 -определитель графа
-определитель графа
Pk-коэффициент передачи k пути от входа к выходу
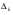 -определитель всех касающихся контуров при удалении k-ого пути
-определитель всех касающихся контуров при удалении k-ого пути
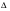 =1-(сумма коэффициентов передачи всех отдельных контуров)+(сумма всевозможных произведений из двух некасающихся контуров) - (сумма всевозможных комбинаций из трех некасающихся контуров)+…+…
=1-(сумма коэффициентов передачи всех отдельных контуров)+(сумма всевозможных произведений из двух некасающихся контуров) - (сумма всевозможных комбинаций из трех некасающихся контуров)+…+…
Последовательность нахождения w(p) по формуле Мейсона:
В данном случае есть 1 путь от входа к выходу:
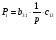
В системе имеется 4 замкнутых контуров:
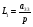
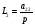
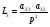
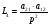
Определитель системы включает 4 контура и 2 пары некасающихся контуров L1,L2; L1,L4
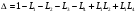
Количество сомножителей равно количеству прямых путей. Выражение для
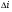 записывается как выражение для
записывается как выражение для 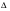 , но разрываются контуры, через которые проходит прямой путь Pi.
, но разрываются контуры, через которые проходит прямой путь Pi.
Сомножитель 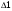 для первого пути. При размыкании первого пути 2 контура размыкаются, кроме L2,L4
для первого пути. При размыкании первого пути 2 контура размыкаются, кроме L2,L4
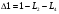
Запишем и преобразуем выражение передаточной функции:
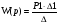
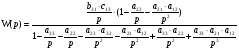
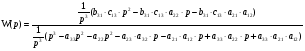


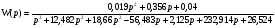
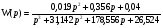
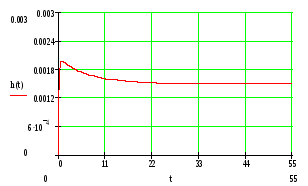
Найдем переходную функцию и построим ее график:
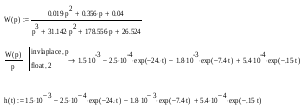
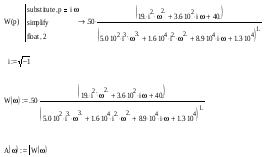 Найдем амплитудно-частотную характеристику (АЧХ):
Найдем амплитудно-частотную характеристику (АЧХ):
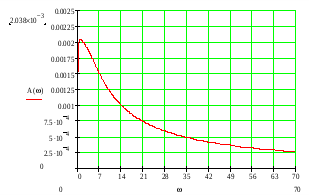 Найдем фаза частотную характеристику (ФЧХ):
Найдем фаза частотную характеристику (ФЧХ):
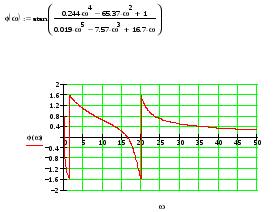
Определим оценки качества системы: прямые и косвенные.
Прямые оценки определяются графически по графику переходного процесса.
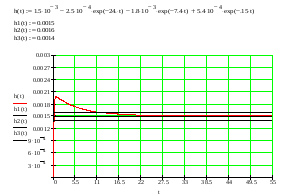
Время переходного процесса: tn=11
Перерегулирование:
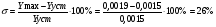
Колебательность: п=0,5
Время нарастания регулируемой величины: t=0,385
Время первого согласования: tm=0,66
Косвенные оценки качества системы определяются по графику АЧХ.
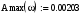
Колебательность:
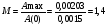
Резонансная частота: p=0,83
Частота среза: сp=10
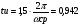
Полоса пропускания частот: 
II-часть
Задание1: По заданной корреляционной функции Kx() определить спектральную плотность Sx() для белого шума, который подается на вход формирующего фильтра.
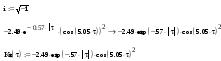 По данной корреляционной функции определим спектральную плотность:
По данной корреляционной функции определим спектральную плотность:
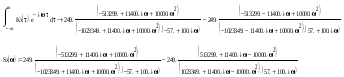
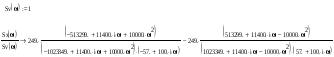

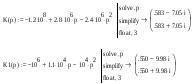 Найдем корни характеристических уравнений передаточной функции фильтра:
Найдем корни характеристических уравнений передаточной функции фильтра:
Изобразим эти корни на комплекснрй плоскости:
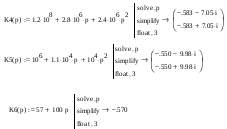
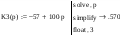
Система будет устойчивой, если корни характеристического уравнения лежат во 2-ом квадранте, следовательно, условию устойчивости системы соответствуют корни:
P7= -0,583+7,05i
P9= - 0,550+9,98i
P10= -0,570
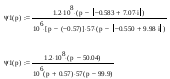 Из этого следует, что передаточная функция фильтра будет иметь
Из этого следует, что передаточная функция фильтра будет иметь
следующий вид:
С учетом фильтра наша схема будет иметь следующий вид:
W(p) (р)
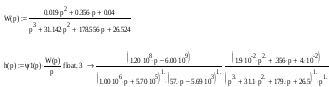
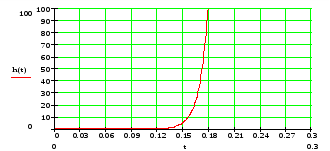 Найдем переходную функцию данной системы, построим ее график и определим прямые оценки качества системы.
Найдем переходную функцию данной системы, построим ее график и определим прямые оценки качества системы.
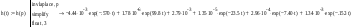
Вывод: По графику видно, что фильтр вносит в систему изменения, приводящие к неустойчивости системы. Вследствие чего оценки качества системы определить нельзя.

Нравится материал? Поддержи автора!
Ещё документы из категории коммуникации, связь:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ