Построение годографов Михайлова при помощи пакета MATHCAD
построение годографов михайлова при помощи пакета «mathcad»
Цель работы заключается в необходимости получения простого и наглядного инструмента для решения задач расчёта устойчивости систем автоматического управления, что является обязательным условием работоспособности любого промышленного робота и манипулятора.
1 Понятие об устойчивости системы
Как видно из цели исследования, необходимым условием работоспособности системы автоматического управления (САУ), является её устойчивость. Под устойчивостью принято понимать свойство системы восстанавливать состояние равновесия, из которого она была выведена под влиянием возмущающих факторов после прекращения их воздействия [1]. Если система не способна возвращаться в состояние равновесия, которое было нарушено в процессе работы, то для практического использования она непригодна.
На практике для определения устойчивости САУ используют критерии устойчивости, то есть правила, с помощью которых можно определить устойчива ли система, не прибегая к решению дифференциальных уравнений. Одним из таких критериев, есть критерий устойчивости Михайлова.
2 Критерий устойчивости Михайлова
Данный критерий основан на связи характера переходного процесса системы с амплитудой и фазой вынужденных колебаний, устанавливающихся в системе при синусоидальном воздействии. Анализ устойчивости системы этим методом сводится к построению по характеристическому многочлену замкнутой системы (знаменатель передаточной функции), комплексной частотной функции (характеристического вектора):
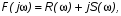 (1)
(1)
где 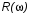 и
и 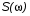 – соответственно вещественная и мнимая части знаменателя передаточной функции, по виду которой можно судить об устойчивости системы.
– соответственно вещественная и мнимая части знаменателя передаточной функции, по виду которой можно судить об устойчивости системы.
Если задаваться различными значениями частоты 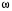 и откладывать
и откладывать 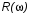 по горизонтальной, а
по горизонтальной, а 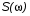 по вертикальной осям декартовой системы координат, то будет получена кривая, называемая годографом характеристического вектора или годографом Михайлова.
по вертикальной осям декартовой системы координат, то будет получена кривая, называемая годографом характеристического вектора или годографом Михайлова.
В таком случае, критерий устойчивости Михайлова может быть сформулирован следующим образом: замкнутая САУ устойчива, если комплексная частотная функция 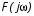 , начинаясь на действительной положительной оси, при изменении частоты
, начинаясь на действительной положительной оси, при изменении частоты 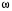 от 0 до ∞ огибает против часовой стрелки начало координат, проходя последовательно n квадрантов, где n – порядок характеристического уравнения системы, т. е.
от 0 до ∞ огибает против часовой стрелки начало координат, проходя последовательно n квадрантов, где n – порядок характеристического уравнения системы, т. е.
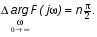 (2)
(2)
jS(ω)
R(ω)
0
а)
n=1
n=2
n=3
n=4
n=5
jS(ω)
R(ω)
0
б)
3
2
1
Рисунок 1 – Амплитудно-фазовые характеристики (годографы) критерия Михайлова: а) – устойчивой системы; б) – неустойчивой системы (1, 2) и системы на границе устойчивости (3)
На рис. 1 показаны примеры перемещения годографов Михайлова для различных систем с изменяющимся порядком n характеристического уравнения.
3 Алгоритм построения годографа Михайлова
Рассмотрим последовательность расчёта критерия устойчивости Михайлова и сформируем алгоритм построения годографа, используя математический пакет «MathCad», на приведенных ниже примерах.
Пример 1. Используя критерий Михайлова, определим устойчивость системы автоматического управления электроприводом манипулятора промышленного робота (МПР). Структурная схема САУ электроприводом МПР изображена на рис. 2.
Uз(s)
ΔU(s)

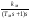
Uя(s)
ω(s)
kдс
Uдс(s)
(-)
Рисунок 2 – Структурная схема САУ электроприводом МПР
Передаточная функция данной САУ имеет следующее выражение [2]:
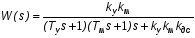 (3)
(3)
или
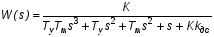 (4)
(4)
где kу – коэффициент усиления усилителя, kм – коэффициент пропорциональности частоты вращения двигателя величине напряжения на якоре, Tу – электромагнитная постоянная времени усилителя, Tм – электромеханическая постоянная времени двигателя с учётом инерции нагрузки (по своим динамическим характеристикам двигатель представляет собой передаточную функцию последовательно соединённых инерционного и интегрирующего звеньев), kдс – коэффициент пропорциональности между входной и выходной величинами датчика скорости, K – коэффициент усиления главной цепи: 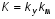 .
.
Подставим численные значения в выражение передаточной функции:
K = 100 град / (В∙с); kдс = 0,01 В / (град∙с); Tу = 0,01 с; Tм = 0,1с.
Получим:
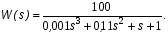 (5)
(5)
Далее запишем характеристический многочлен замкнутой системы 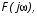 заменив s на
заменив s на 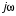 :
:
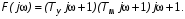 (6)
(6)
С помощью (1) выделим вещественную и мнимую части и подставим численные значения в полученную комплексную частотную функцию:
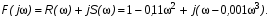 (7)
(7)
Имея данные в виде (7), перейдём непосредственно к использованию математического пакета «MathCad».
Для этого в верхнем меню выберем «Новый…» – «Пустой документ», в котором будем формировать программу построения годографа Михайлова, используя нижеприведенный алгоритм.
Шаг 1. Задать разрешение годографа диапазоном значений индекса i. Например:
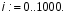 (8)
(8)
Шаг 2. Определить исследуемый диапазон и шаг частоты  , используя значения индекса i (обычно, для практических расчётов, максимальная величина частоты
, используя значения индекса i (обычно, для практических расчётов, максимальная величина частоты 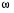 не превышает значения 1000, в нашем же примере – достаточно принять
не превышает значения 1000, в нашем же примере – достаточно принять 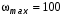 с частотным шагом 0,1):
с частотным шагом 0,1):
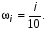 (9)
(9)
Шаг 3. Полученные вещественную 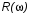 и мнимую
и мнимую 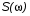 части характеристического уравнения, зададим численными значениями (в данном случае используя (7)) в виде:
части характеристического уравнения, зададим численными значениями (в данном случае используя (7)) в виде:
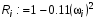 (10)
(10)
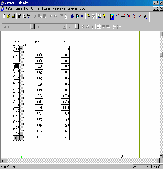 и
и
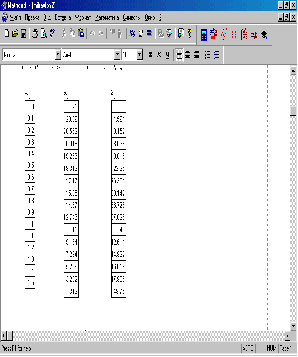
Рисунок 3 – Массивы значений , и , рассчитанные в «MathCad»
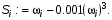 (11)
(11)
Шаг 4. В результате вычислений (9), (10) и (11), получаются массивы значений частоты 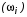 , а также вещественной
, а также вещественной 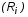 и мнимой
и мнимой 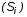 частей (рис. 3).
частей (рис. 3).
Шаг 5. Далее имея рассчитанные массивы значений 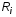 и
и 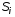 , переходим к построению годографа Михайлова, используя встроенную функцию «MathCad» – «Инструменты графиков», выбрать «Декартов график». Здесь необходимо определить идентификаторы осей (в данном случае ось абсцисс соответствует вещественной части
, переходим к построению годографа Михайлова, используя встроенную функцию «MathCad» – «Инструменты графиков», выбрать «Декартов график». Здесь необходимо определить идентификаторы осей (в данном случае ось абсцисс соответствует вещественной части 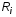 , а ординат – мнимой части
, а ординат – мнимой части 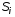 ) и параметры графика в подменю «Формат…». В результате получим график комплексной частотной функции, приведенный на рис. 4.
) и параметры графика в подменю «Формат…». В результате получим график комплексной частотной функции, приведенный на рис. 4.
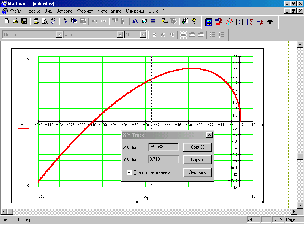
Рисунок 4 – Годограф Михайлова для САУ электроприводом МПР
Используя функцию «Трассировка…» (пунктирные линии на рис. 4), можно определить, в соответствующем трассировке окне, точные значения годографа в любой точке рассчитанных массивов.
Таким образом, по рассчитанным данным, построенный годограф Михайлова, начинаясь на действительной положительной полуоси, огибает против часовой стрелки начало координат, проходя последовательно три квадранта, что соответствует порядку характеристического уравнения. Следовательно, данная САУ электроприводом МПР – устойчива.
В соответствии с изложенным алгоритмом, рассмотрим ещё один пример расчёта критерия устойчивости Михайлова и построения комплексной частотной функции.
Пример 2. На современных автомобильных заводах широко применяются большие сварочные роботы (рис. 5). Наконечник сварочного узла (НСУ) подводится к различным местам кузова автомобиля, быстро и точно совершает необходимые действия. Требуется определить устойчивость по критерию Михайлова САУ позиционированием НСУ, структурная схема которой изображена на рис. 6.
X(s)
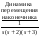
Y(s)
(-)
Характеристическое уравнение данной САУ будет иметь вид [1]:
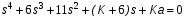 (12)
(12)
где K – варьируемый коэффициент усиления системы, a – определённая положительная константа.
Подставим в (12) численные значения: K = 40; a = 0,525.
Имеем:
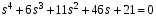 (13)
(13)
Далее путём замены s на 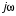 , получим функцию Михайлова:
, получим функцию Михайлова:
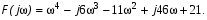 (14)
(14)
Перед тем, как выделить вещественную и мнимую части, запишем (1) в несколько усовершенствованном виде, с целью универсального использования для различных порядков n:
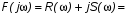
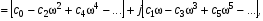 (15)
(15)
где с – соответствующий постоянный коэффициент при определённом порядке частоты 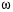 .
.
Применяя (15) к нашей задаче, получим:
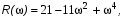 (16)
(16)
а также
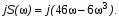 (17)
(17)
Имея данные в виде (16) и (17), приступим к вышеупомянутому алгоритму построения годографа Михайлова с помощью «MathCad».
Шаг 1. Зададим диапазон индекса i:
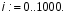 (18)
(18)
Шаг 2. Определим исследуемый диапазон и шаг частоты 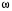 (примем
(примем 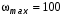 с частотным шагом 0,1):
с частотным шагом 0,1):
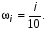 (19)
(19)
Шаг 3. Введём вещественную 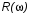 (16) и мнимую
(16) и мнимую 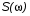 (17) части характеристического уравнения:
(17) части характеристического уравнения:
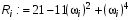 (20)
(20)
и
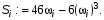 (21)
(21)
Шаг 4. При выполнении вычислений (19), (20) и (21), формируются массивы значений частоты 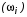 , вещественной
, вещественной 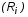 и мнимой
и мнимой 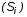 частей (рис. 7).
частей (рис. 7).
Шаг 5. Имея рассчитанные массивы значений 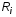 и
и 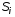 , подобно предыдущему примеру, построим частотную функцию Михайлова. После определения параметров графика, получим годограф, приведенный на рис. 8.
, подобно предыдущему примеру, построим частотную функцию Михайлова. После определения параметров графика, получим годограф, приведенный на рис. 8.
Рисунок 7 – Массивы значений 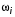 ,
, 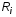 и
и 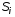 , рассчитанные в «MathCad»
, рассчитанные в «MathCad»
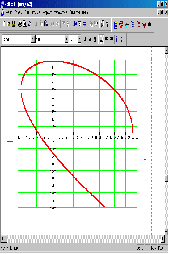
Рисунок 8 – Годограф Михайлова для САУ позиционированием НСУ
На основе анализа полученных данных, можно сделать вывод, что построенный годограф Михайлова, начинаясь на вещественной положительной оси, огибает в положительном направлении начало координат, проходя последовательно четыре квадранта, что соответствует порядку характеристического уравнения. Значит, данная САУ позиционированием НСУ – устойчива.
Что же касается анализа последних публикаций [2] и сравнения с лучшими аналогами [3], то необходимо отметить факт отсутствия подобной функции (построение годографа Михайлова) в пакете «MATLAB» [1, 4], который, обычно, используется для моделирования различных САУ, что, собственно, и послужило главной причиной создания данного алгоритма.
Перспективы развития данной работы заключаются в создании универсального инструмента для анализа комплексной частотной функции Михайлова, способного выполнить все вычисления уже на этапе задания характеристического уравнения, тем самым полностью автоматизируя этот процесс.
Таким образом, для достижения цели, в ходе написания исследования, была решена главная проблема – получение простого и наглядного инструмента для решения задач расчёта устойчивости САУ, что является обязательным условием работоспособности любого промышленного робота и манипулятора. Также были выполнены следующие задачи: сформирован алгоритм построения комплексной частотной функции Михайлова при помощи математического пакета «MathCad», выполнен анализ устойчивости САУ МПР по данному критерию, кроме того, – приведены практические примеры реализации данного алгоритма.
Список использованной литературы
1. Дорф Р. Современные системы управления / Р. Дорф, Р. Бишоп. – М.: Лаборатория Базовых Знаний, 2002. – 832 с.
2. Юревич Е.И. Основы робототехники 2-е издание / Е.И. Юревич. – С-Пб.: БХВ-Петербург, 2005. – 416 с.
3. Yim Y. Modular Robots / Y. Yim, Y. Zhang, D. Daff // IEEE SPECTRUM. – 2002. – # 2. – P. 30 – 34.
4. Олссон Г. Цифровые системы автоматизации и управления / Г. Олссон, Дж. Пиани. – С-Пб.: Невский Диалект, 2001. – 557 с.

Нравится материал? Поддержи автора!
Ещё документы из категории коммуникации, связь:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ