Расчет зеркальной параболической антенны с облучателем в виде конического рупора



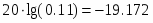
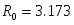
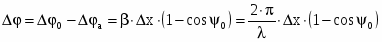
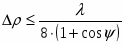

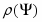
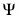
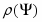
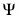
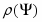
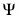
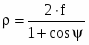
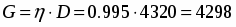
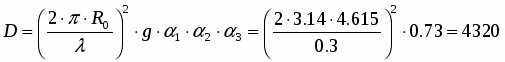
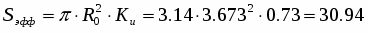
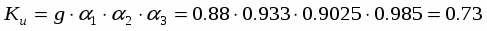
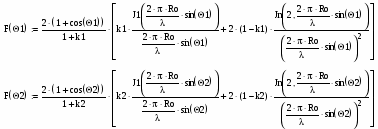
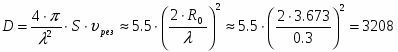
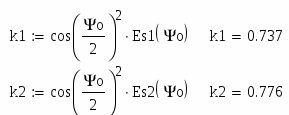
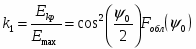
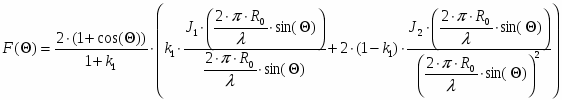
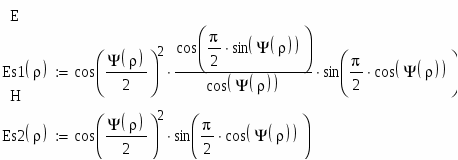
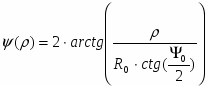
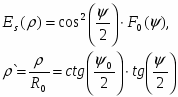
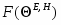
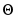
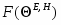
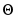
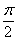
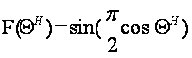
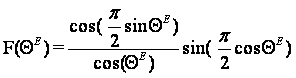
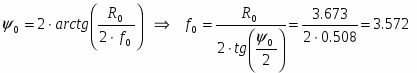
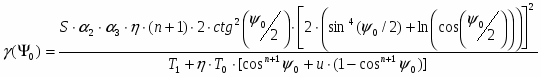
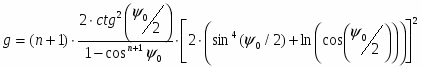
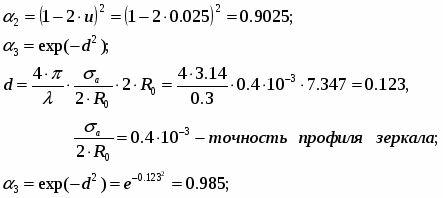
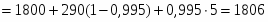
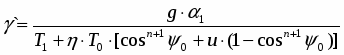
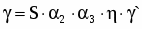
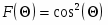
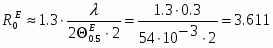
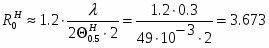
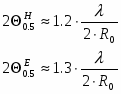
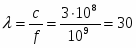
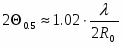
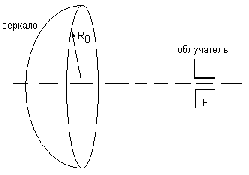
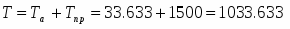
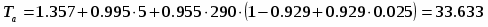
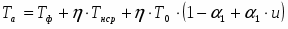
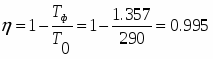
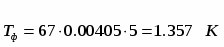
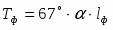
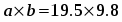 Некоммерческое акционерное общество
Некоммерческое акционерное общество
«АЛМАТИНСКИЙ УНИВЕРСИТЕТ ЭНЕРГЕТИКИ И СВЯЗИ»
Кафедра РТ
Дисциплина АФУиРРВ
Курсовая работа
Специальность:
050719 – Радиотехника, электроника и телекоммуникации
Выполнил: студент Джуматаев Е.Б.
Алматы 2010
ИСХОДНЫЕ ДАННЫЕ
ВВЕДЕНИЕ
1. РАСЧЕТ ГЕОМЕТРИЧЕСКИХ И ЭЛЕКТРОДИНАМИЧЕСКИХ ПАРАМЕТРОВ ОБЛУЧАТЕЛЯ И ПАРАБОЛОИДА
1.1 Выбор фидера. Определение шумовой температуры фидерного тракта
1.2 Определение диаметра раскрыва
1.3 Аппроксимация аналитического вида ДН облучателя функцией вида cosn/2
1.4 Определение угла раскрыва и фокусного расстояния зеркальной антенны
2. РАСЧЕТ ГЕОМЕТРИЧЕСКИХ И ЭЛЕКТРОДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК ПОЛЯ
2.1 Диаграммы направленности облучателя
2.1 Распределение поля в апертуре зеркала
3. РАСЧЕТ ПРОСТРАНСТВЕННОЙ ДИАГРАММЫ НАПРАВЛЕННОСТИ И ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ПАРАБОЛИЧЕСКОЙ АНТЕННЫ
4 КОНСТРУКТИВНЫЙ РАСЧЕТ АНТЕННЫ
4.1 Расчет профиля зеркала
4.2 Выбор конструкции зеркала
4.3 Определение допусков на точность изготовления
5. СОПОСТАВЛЕНИЕ РАСЧЕТНОГО И ЗАДАННОГО УРОВНЯ БОКОВЫХ ЛЕПЕСТКОВ, ВЫРАБОТКА РЕКОМЕНДАЦИИ ДЛЯ ОБЕСПЕЧЕНИЯ СООТВЕТСТВИЯ ЭТИХ УРОВНЕЙ
ЗАКЛЮЧЕНИЕ
СПИСОК ЛИТЕРАТУРЫ
ИСХОДНЫЕ ДАННЫЕ
Рассчитать малошумящую параболическую антенну. Исходные данные:
Частота сигнала генератора, подводимого к антенне, f = 1,0 ГГц;
Ширина главного лепестка ДН на уровне половинной мощности 0.5
Н0.5 = 49 мрад;
Е0.5 = 54 мрад;
Уровень боковых лепестков (- 17) дБ;
Тип облучателя: Полуволновой вибратор с дисковым контррефлектором;
Средняя яркостная температура неба Тнср = 5 К;
Температура шумов приемника Тпр = 1800 К;
Длина фидерной линии lф=5 м.
Параболические антенны в последнее время находят все более широкое применение в космических и радиорелейных линиях связи. В 1888 году известный немецкий физик Г. Герц в своих опытах по СВЧ оптике впервые применил в качестве фокусирующего устройства параболический цилиндр. Интерес к зеркальным антеннам не ослабевает и в наши дни в связи со стремительным развитием космических радиотехнических систем и комплексов.
Достаточная простота и легкость конструкции, возможность формирования самых разнообразных диаграмм направленности, высокий КПД, малая шумовая температура – вот основные достоинства, зеркальных антенн, обуславливающих их широкое применение в современных радиосистемах.
Целью данной курсовой является освоение методики проектирования зеркальных параболических антенн: определение их основных электродинамических параметров и конструктивный расчет.
В курсовой работе определение поля излучения параболической антенны производится апертурным методом, который широко применяем при проектировании зеркальных антенн.
1 РАСЧЕТ ГЕОМЕТРИЧЕСКИХ И ЭЛЕКТРОДИНАМИЧЕСКИХ ПАРАМЕТРОВ ОБЛУЧАТЕЛЯ И ПАРАБОЛОИДА
1.1 Выбор фидера. Определение шумовой температуры фидерного тракта
В качестве фидера будет использован прямоугольный волновод. Его параметры для частоты f = 1.0 ГГц даны в [1], приложение А:
см
= 0.00405 дБ/м
Шумовая температура фидерного тракта Тф:
,
где α – коэффициент затухания линии передачи [дБ/м],
lф – длина фидерной линии [м].
.
Выразим КПД из формулы:
Тф=T0·(1-КПД),
где Т0=290 К.
Тогда КПД равен:
.
Шумовая температура антенной системы:
1 = 1 - cosn+10 = 0.929 (см. пункт 1.4)
К;
К.
1.2 Определение диаметра раскрыва
Зеркальная антенна – направленная антенна, содержащая первичный излучатель и отражатель антенны в виде металлической поверхности. Параболическая зеркальная антенна представлена на рисунке 1.
Рисунок 1 – Зеркальная параболическая антенна
В случае равномерно возбуждённого раскрыва параболического зеркала ширина ДН приближённо определяется:
,
где 0.5 – ширина диаграммы направленности на уровне половинной мощности, рад.;
- длина волны излучаемого (принимаемого) антенной радиосигнала;
R0 – радиус раскрыва зеркала (рисунок 1).
Длина волны определяется по формуле:
cм.
Неравномерное возбуждение раскрыва зеркала приводит к некоторому расширению главного лепестка ДН, так как уменьшается эффективная площадь раскрыва. Чаще всего диаграммы направленности зеркальных антенн не обладают осевой симметрией, т.е. ширина главного лепестка в плоскостях Е и Н различна. В большинстве практических случаев это влечёт за собой следующее изменение:
где Н0.5 , Е0.5 ширина ДН соответственно в плоскостях H и E.
Для Е и Н плоскостей соответственно найдем радиусы раскрыва:
м;
м.
Исходя из исходных данных о ширине диаграммы направленности в обеих плоскостях, можно определить диаметр раскрыва dp = 2 R0, причем, из полученных двух значений диаметра следует выбрать наибольшее. Следовательно,
R0 = 3.673 м,
dp = 2R0 = 23.673 = 7.346 м.
1.3 Аппроксимация аналитического вида ДН облучателя функцией вида cosn/2
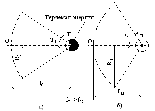
В зависимости от размещения облучателя относительно зеркала можно получить то или иное значение КНД. При определенном оптимальном отношении Ro/fo КНД наибольший. Это объясняется тем, что количество теряемой энергии зависит от формы диаграммы направленности облучателя и от отношения Ro/fo. При уменьшении отношения Ro/fo от оптимального КНД уменьшается, так как увеличивается часть энергии, проходящей мимо зеркала. С другой стороны, увеличение этого отношения также приводит к уменьшению КНД в связи с более сильным отклонением закона распределения возбуждения от равномерного. Оптимальное значение Ro/fo определяется по аппроксимированной нормированной ДН облучателя (аппроксимация функцией вида F()=cosn2(), где n определяет степень вытянутости ДН облучателя).
Рисунок 2 - Варианты размещения облучателя
Для вибратора с контррефлектором в виде диска:
n=4; R0/f0=1.0…1.25; ν=0.82
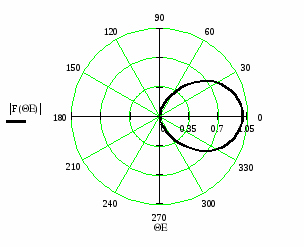
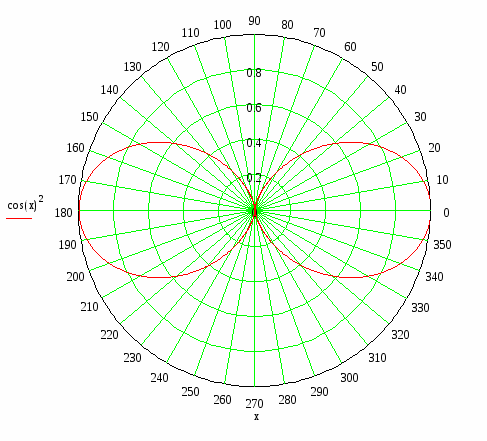
Аппроксимированная нормированная ДН представлена на рисунке 3.
Рисунок 3 – Апроксимированная нормированная ДН облучателя
1.4 Определение угла раскрыва и фокусного расстояния зеркальной антенны.
С точки зрения оптимизации геометрии антенны по максимальному отношению сигналшум необходимо произвести следующий расчет.
Чувствительность определяется по формуле:
,
где первые четыре коэффициента не зависят от о, а ' вычисляется:
,
где Т1
u = (0.02 – 0.03) – коэффициент, учитывающий «переливание» части мощности облучателя через края зеркала:
u = 0.025;
S – площадь апертуры зеркала
S= πR2 = 3.1423.6732 = 42.394 м2;
n = 4 – определяется типом облучателя;
1 = 1 - cosn+10;
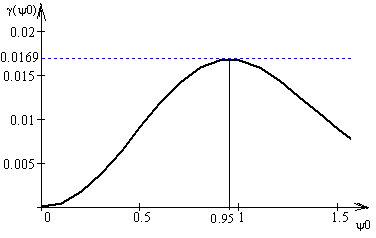
Построим график функции γ(0), по максимуму которого определим угол раскрыва зеркала:
Таблица 1 – Аргументы функции γ(0) и её значения
0
0.301
0.601
0.901
1.201
1.401
1.501
γ(0)
3.779e-3
0.012
0.017
0.014
0.011
8.863e-3
По графику (рисунок 1.4) можно определить:
0 = 0.95 рад = 54.431,
тогда
1 = 1 – cos5(54.431) = 0.933,
g = 0.88,
` = 4.466 10-4,
= 0.0169.
Фокусное расстояние f0 может быть найдено из следующего соотношения:
зеркальная антенна облучатель зеркало
м.
В зависимости от размещения облучателя относительно зеркала можно получить то или иное значение КНД. При определенном оптимальном отношении R0/f0 КНД наибольший. Заданный интервал отношения R0/f0 = (1.0÷1.25). Расчетное отношение R0/f0 = 1.029, что удовлетворяет условию.
2. РАСЧЕТ ГЕОМЕТРИЧЕСКИХ И ЭЛЕКТРОДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК ПОЛЯ
2.1 Диаграммы направленности облучателя
Полуволновой симметричный вибратор с контррефлектором в виде диска
Фазовый центр вибратора с контррефлектором в виде диска лежит между вибратором и контррефлектором несколько ближе к последнему. Обычно контррефлекторы выполняются в виде дисков диаметром 2d = (0.7 ... 0.8), при этом ДН имеет форму, близкую к диаграмме с осевой симметрией. Расстояние между вибратором и контррефлектором выбирается близким к четверти длины волны, а длина вибратора - к половине длины волны (2l /2).
Диаграмма направленности такого облучателя в Е плоскости рассчитывается по формуле [11]
Рисунок 5 – ДН облучателя в плоскости Е
а в Н плоскости - по формуле
Рисунок 6 – ДН облучателя в плоскости H
Эти формулы справедливы для E и H менее .
Таблица 2 – Расчет ДН конического рупора
, град
0
10
20
30
40
50
60
70
80
90
1
1
0.995
0.977
0.931
0.843
0.701
0.503
0.258
0.087
, град
-90
-80
-70
-60
-50
-40
-30
-20
-10
0
0
0.27
0.513
0.708
0.848
0.934
0.978
0.996
1
1
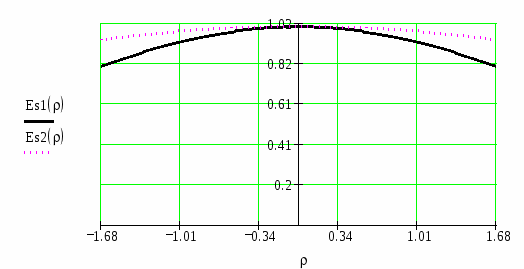
2.1 Распределение поля в апертуре зеркала
Расчет распределения поля в апертуре зеркала осуществляется по следующим формулам:
где F0() – диаграмма направленности облучателя,
0 – угол раскрыва,
– текущий угол.
Зависимость угла от текущего радиуса :
,
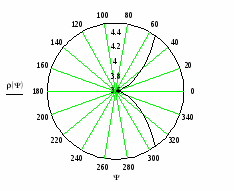
ρ, м
3. РАСЧЕТ ПРОСТРАНСТВЕННОЙ ДИАГРАММЫ НАПРАВЛЕННОСТИ И ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ПАРАБОЛИЧЕСКОЙ АНТЕННЫ
Инженерный расчёт пространственной диаграммы направленности ДН параболической антенны часто сводится к определению ДН идеальной круглой синфазной площадки с неравномерным распределением напряжённости возбуждающего поля. В данном случае распределение напряжённости возбуждающего поля в основном определяется ДН облучателя в соответствующей плоскости. Выражение для нормированной ДН зеркальной параболической антенны при этом имеет вид:
,
где J1, J2 – цилиндрические функции Бесселя первого и второго порядка.
- Коэффициент, показывающий во сколько раз амплитуда возбуждающего поля, на краю раскрыва меньше амплитуды в центре раскрыва в соответствующей плоскости с учётом различий расстояний от облучателя до центра зеркала и до края зеркала;
Екр, Емах – амплитуды поля на краю и в центре раскрыва.
ДН зеркальной параболической антенны имеет следующий вид (рисунок 2.5).
Приближенно коэффициент направленного действия зеркальной антенны определяется выражением:
, г
де
S – площадь раскрыва;
υрез – результирующий коэффициент использования поверхности
F(ϴ) ϴ, рад
Рисунок 8 – Пространственная ДН параболической антенны
Коэффициент использования поверхности:
Эффективная площадь антенны:
м2.
Коэффициент направленного действия:
Коэффициент усиления антенны:
4. КОНСТРУКТИВНЫЙ РАСЧЕТ АНТЕННЫ
4.1 Расчет профиля зеркала
Зеркальные антенны имеют наибольший КНД при синфазном возбуждении раскрыва (плоский фазовый фронт волны). Параболический профиль зеркала обеспечивает одинаковые длины электрических путей от облучателя, установленного в фокусе параболоида вращения, до каждой точки плоскости раскрыва (свойство параболы). В полярной системе координат парабола описывается уравнением
,
Где , - полярные координаты;
f = 3.572 м - фокусное расстояние;
изменяется от 0 до 0=0.95 рад.
Рисунок 9 – Плоский фазовый фронт волны
Таблица 3 – Расчет профиля зеркала
, рад
-0.95
-0.85
-0.75
-0.65
-0.55
-0.45
-0.35
-0.25
-0.15
4.516
4.303
4.125
3.977
3.856
3.759
3.683
3.628
3.592
, рад
-0.05
0.05
0.15
0.25
0.35
0.45
0.55
0.65
0.75
3.574
3.574
3.592
3.628
3.683
3.759
3.856
3.977
4.125
, рад
0.85
0.95
4.303
4.516
4.2 Выбор конструкции зеркала
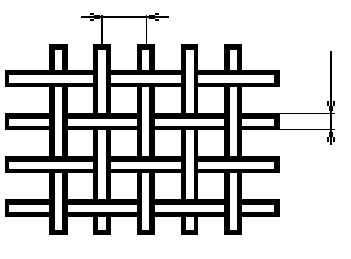
С целью уменьшения веса и ветровых нагрузок поверхность зеркала часто выполняется перфорированной, или сетчатой
Рисунок 10 – Конструкция зеркала
При такой конструкции зеркала часть энергии просачивается сквозь него, образую нежелательное излучение. Допустимым является значение коэффициента прохождения в обратном направлении.
,
где Рпад, Робр – мощность излучения падающего на зеркало и в обратном направлении, соответственно.
Двухлинейная сетка работает удовлетворительно при расстоянии между проводниками меньше 0.1 и диаметре проводов не менее 0.01.
dп = 0.1 0.3 = 3 см;
d = 0.01 0.3 = 3 мм.
4.3 Определение допусков на точность изготовления
Неточность изготовления зеркала вызывает несинфазность поля в раскрыве. Допустимыми являются фазовые искажения поля в раскрыве зеркала не более ± /4. При этом уменьшение коэффициента усиления антенны не превышает нескольких процентов.
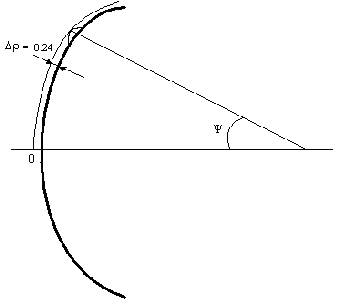
Пусть поверхность параболоида имеет некоторые неровности (выступы и углубления). Наибольшее отклонение от идеальной поверхности в направлении обозначим через Δ.
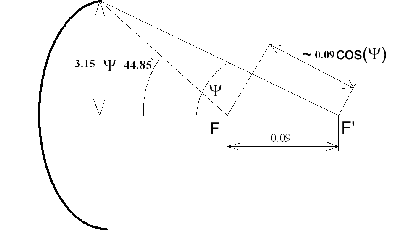
Рисунок 11 – Допуски на точность изготовления зеркала
Путь луча, отраженного от неровности в месте наибольшего отклонения от изменяется при этом на величину + cos, а соответствующий сдвиг фаз составит величину = (1+cos), и он не должен превышать величину 4, отсюда получаем
Анализ полученного выражения для показывает, что вблизи центра параболоида ( = 0) необходимая точность изготовления зеркала наивысшая. Здесь наибольшее отклонение от идеальной поверхности не должно превосходить величины 16 (т.е. 0.0023) у кромки параболоида требования к точности получаются наименьшими. Точность установки облучателя также определяется нормами на наибольшие допустимые фазовые искажения поля в раскрыве. Пусть фазовый облучатель смещен на х (рисунок 4.4). Тогда длины путей лучей от фазового центра до раскрыва увеличиваются.
Рисунок 12 — Допуски на точность установки облучателя
Наибольшее удлинение пути происходит у лучей, падающих на вершину зеркала. Это удлинение путей при малых смещениях можно приблизительно определить как хcos. Тогда изменение фазы составит величину
, где
0, а – фазовые искажения, возникающие из-за неточности установки облучателя, в центре и на краю раскрыва, соответственно. Эта величина не должна превышать /4, отсюда получаем:
Таким образом, с увеличением угла раскрыва точность и установка облучателя в фокусе повышается.
5. СОПОСТАВЛЕНИЕ РАСЧЕТНОГО И ЗАДАННОГО УРОВНЯ БОКОВЫХ ЛЕПЕСТКОВ, ВЫРАБОТКА РЕКОМЕНДАЦИИ ДЛЯ ОБЕСПЕЧЕНИЯ СООТВЕТСТВИЯ ЭТИХ УРОВНЕЙ
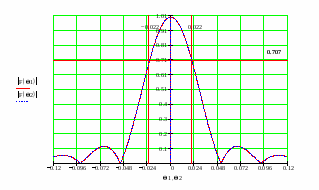
По графику, изображенному на рисунке 8, найдем ширину ДН на уровне половинной мощности:
2H0.5 = 44 мрад, что меньше заданного значения 2H0.5 = 49 мрад на 10,2% и 2Е0.5=48 меньше значения 2Е0.5 = 54 мрад на 11,1%.
Для увеличения ширины ДН необходимо уменьшить радиус параболоида.
Пусть радиус параболоида будет равным м. Тогда получаем график ДН:
Рисунок 13 – ДН антенны
По графику определим ширину 2H0.5 = 49 мрад, равно значению 2H0.5 = 49 мрад и 2Е0.5 = 54 равное заданному значением 2Е0.5 = 54 мрад. Достигнут компромисс.
Уровень УБЛ возьму по максимальному уровню боковых лепестков.
Найдем УБЛ:
УБЛ = 0.11
дБ
Допустимое значение УБЛ = -17 дБ, значит вычисленное значение допустимо, потому что уровень боковых лепестков ослабляется дополнительно на 1.416 чем задано по условию, т.о. придавая ей большую узконаправленность.
ЗАКЛЮЧЕНИЕ
В данной курсовой работе была спроектирована зеркальная параболическая антенна с облучателем в виде конического рупора. При расчете геометрических и электродинамических характеристик облучателя и параболоида исходные данные немного отклоняются от вычисленных значений: отклонение ширины ДН на уровне половинной мощности в плоскости E составляет 18,5%, а в плоскости H – 10,2%. Причиной этому явилась идеализация устройства (использовалась идеальная модель), использование аппроксимации при вычислениях. В реальных системах необходимо учитывать воздействие многих посторонних факторов, влияние которых может существенно повлиять на результат расчётов.
Однако внесение некоторых преобразований (уменьшение радиуса параболоида до м) позволяет прийти к компромиссу. При этом значении отклонения ширины ДН на уровне половинной мощности в плоскостях H и E отсутствуют.
СПИСОК ЛИТЕРАТУРЫ
Гончаров В.Л. Методические указания и задание к выполнению курсовой работе. Алматы: АИЭС – 2007
Антенны и устройства СВЧ. Проектирование фазированных антенных решеток/ Под ред. проф. Д.И. Воскресенского. – М.: Советское радио, 1994.
Кочержевский Г.М., Ерохин Г.А., Козырев Н.Д. Антенно-фидерные устройства. - М.: Радио и связь, 1989.
Регламент радиосвязи. Т.1. – М.: Радио и связь, 1995.
Сазонов Д.М. Антенны и устройства СВЧ. – М.: Высшая школа, 1988.
Спутниковая связь и вещание/ Под ред. Кантора Л.А. – М.: Радио и связь, 1987.
Хмель В.Ф., Чаплин А.Ф., Шумлянский И.И. Антенны и устройства СВЧ. – Киев: Вища школа, 1990.

Нравится материал? Поддержи автора!
Ещё документы из категории коммуникации, связь:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ