Разработка арифметико-логического устройства, выполняющего операции сложения и вычитания в прямом двоичном коде




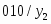

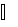
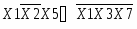
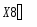
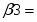
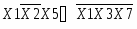

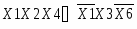
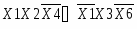


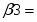
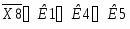
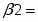
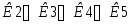

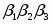
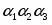

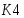
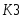
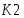
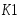
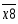
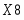
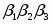
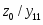
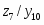
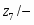
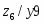
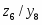

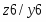
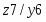
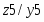
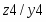

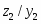

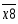
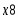
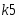
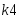

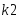
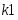

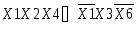
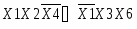

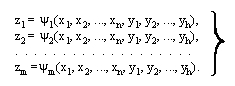


Курсовая работа
На тему:
«Разработка арифметико-логического устройства, выполняющего операции сложения и вычитания в прямом двоичном коде»
Запорожье 2010 г.
Реферат
В данном курсовом проекте производится разработка управляющего автомата реализующего функции устройства для выполнения сложения и вычитания в прямых кодах с учетом знака операндов и знака операции, каноническим методом структурного синтеза цифровых автоматов.
Рассмотрен абстрактный цифровой автомат Мили заданного устройства, алгоритм его работы, таблицы прошивки и возбуждения постоянного запоминающего устройства, составлены функции возбуждения. Также составлены функциональная и электрическая принципиальная схемы.
Арифметико-логическое устройство, алгоритм, абстрактный автомат, граф автомата, таблица переходов-выходов, кодирование, ПЗУ, таблица возбуждений ПЗУ, функция возбуждений ПЗУ, структурная схема, схема электрическая принципиальная.
цифровой устройство автомат алгоритм
Введение
Логические устройства, работающие с цифровым сигналом получили широкое применение в электронике. Стали развиваться науки связанные с цифровыми устройствами: «Цифровая схематехника», «Цифровые автоматы».
Основой всех цифровых устройств являются простейшие логические элементы, выполняющие простейшие логические операции алгебры-логики. Все более сложные цифровые устройства можно представить в виде простейших устройств – логических элементов. Конструирование электронных схем и эффективное применение цифровых устройств невозможно без представлений о принципах их действия и основных параметрах.
Структурная схема любого ЦА состоит из трех частей: запоминающей части с дешифратором, схемы формирования сигналов возбуждения триггеров запоминающей части, схемы формирования выходных сигналов.
ЗУ с дешифратором содержит тригерный регистр, на котором могут размещаться всевозможные числа, соответствующие требуемым состояниям. Дешифратор расшифровывает число в нужный сигнал состояния, индекс которого совпадает с величиной числа. Входные сигналы, множество которых обозначено через Х, сигналы состояний, множество которых обозначено через S, используются для формирования сигналов возбуждения триггеров, как для автоматов Мили, так и для автоматов Мура, а также для формирования выходных сигналов автоматов Мили.
1. Выполнение операций сложения, вычитания в двоичном коде
Сложение чисел, представленных в двоичном коде, выполняется поразрядно, начиная с младшего разряда. В результате сложения двух первых кодов слагаемых Xo, Yo получается первый разряд суммы Sо и код переноса Pо в следующий разряд. В следующих разрядах код Si будет определяться с учетом переноса из соседнего младшего разряда:
7 0111 5 0101
+ ── + ─────
12 1100
Операция Вычитания в ЭВМ выполняется, так же как и сложение, но при этом отрицательные числа представляются в дополнительном или обратном коде. Смысл перевода отрицательных чисел из прямого в дополнительный и обратный коды поясним на примере с десятичными числами.
Допустим, требуется сложить числа X1=76 и X2=-58. Заменим код отрицательного слагаемого X2 его дополнением до 100, так чтобы [X2] доп=100+X2=42. Сложив числа X1+[X2] доп получим: Y=X1+[X2] доп=76+42=118.
Отбрасывая 1 старшего разряда получим искомый результат 18. Равенство полученного результата истинному объясняется тем, что при формировании дополнительного кода к X2 мы прибавляли 100, а из результата вычитали 100 отбрасыванием старшего разряда.
Y=X1+[X2] доп-100=X1+[X2+100] – 100=76+[-58+100] – 100=18.
При записи двоичного числа в прямом коде в знаковом разряде ставится его знак (0 – плюс, 1 – минус), а само число записывается в естественной форме:
X=13 [X] пр=01101
10 2
X=-13 [X] пр=11101
10 2
Дополнительный код отрицательных двоичных чисел получается заменой двоичных кодов во всех разрядах на взаимно обратные (0 на 1, 1 на 0). После этого к младшему разряду числа добавляется 1. В знаковом разряде отрицательного числа записывается 1.
[-14] доп=[-01110] доп=[10001+1]=10010
Кроме дополнительного кода для представления отрицательных чисел используется обратный код. В этом случае в знаковом разряде записывается 1, а в остальных разрядах цифры заменяются на взаимно обратные
[-14] обр=[-01110] обр=10001
При выполнении арифметических операций с отрицательными числами производится поразрядное сложение слагаемых, начиная с младшего и кончая знаковым разрядом. Если используется дополнительный код, то возможная единица переноса из знакового, разряда отбрасывается, при использовании обратного кода единица переноса знакового разряда суммируется с младшим разрядом полученной суммы. Результат вычисления получается в том коде, в каком были представлены слагаемые. Положительные числа в прямом, обратном и дополнительном кодах имеют одну и ту же форму записи.
2. Структурный синтез цифровых автоматов
2.1 Задача структурного синтеза
Процесс построения схемы автомата обычно разделяют на две относительно независимых стадии: абстрактный и структурный синтез. На стадии абстрактного синтеза, исходя из заданных условий работы, выполняется построение таблиц переходов и выходов автомата. Задачей структурного синтеза является построение функциональной схемы автомата. Исходными данными для стадии структурного синтеза являются таблицы переходов и выходов автомата, система логических элементов, тип элемента памяти, а также дополнительные условия, накладываемые на качество и на работу схемы, например: время работы, допустимость риска, условия связи с внешней средой, стоимость и т.п.
Следует отметить, что исходные данные и круг вопросов, решаемых на стадии структурного синтеза, могут существенно изменяться. Например, в некоторых случаях при структурном синтезе решают задачу выбора искомой схемы. В дальнейшем изложении совокупность исходных данных и задач, а структурного синтеза предполагаются такими, как они описаны в начале настоящего параграфа.
2.2 Обобщенная структурная схема автомата
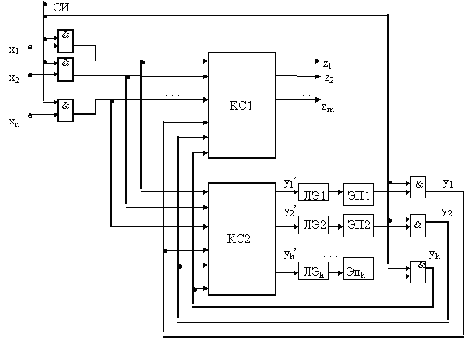
На стадии абстрактного синтеза обычно пользуются представлением автомата в виде одного блока, имеющего один вход и один выход. На стадии структурного синтеза автомат изображают в виде обобщенной структурной схемы, приведенной на рисунке 2.2 т n входных и m выходных каналов, по которым в подавляющем большинстве случаев передаются двоичные сигналы x1, x2,…, xn и z1, z2,…, zm. Переменные x1, x2,…, xn называют входными переменными, а z1, z2,…, zm – выходными переменными или функциями выходов автомата.
Рисунок 2.2. Обобщенная структурная схема автомата
Рассматриваемая схема состоит из двух частей: комбинационной схемы (КС) и набора элементов памяти (ЭП). Переменные y1, y2,…, yh, соответствующие выходным сигналам элементов памяти, называют внутренними переменными автомата. Переменные y1', y2',…, yh' используются в схеме для обозначения входных сигналов, изменяющих состояние элементов памяти, и называют функциями возбуждения. В качестве элементов памяти на практике чаще всего используют элементарные автоматы.
В приведенной схеме наборы значений входных переменных x1, x2,…, xn соответствуют буквам входного алфавита Р абстрактного автомата, наборы выходных переменных z1, z2,…, zm - буквам выходного алфавита W, y1, y2,…, yh - состояниям абстрактного автомата.
2.3 Структурная схема с преобразователями входных и выходных сигналов
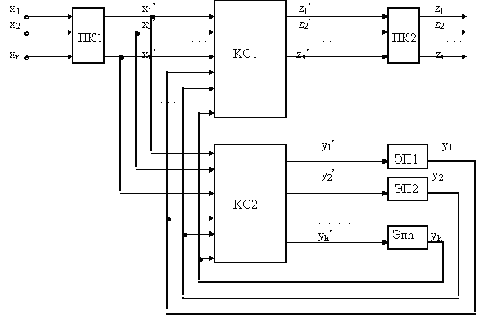
В общем случае комбинационная схема в приведенной структурной схеме автомата может решать несколько различных задач. Если эту схему разбить на подсхемы так, чтобы каждая задача решалась отдельной подсхемой, то структурная схема автомата может быть представлена в виде, изображенном на рис. 2.3. В этой схеме комбинационная схема КС1 вырабатывает функции выхода, КС2 – функции возбуждения, преобразователь кодов ПК1 используется для перекодирования входных сигналов, а преобразователь кодов ПК2 – для преобразования выходных сигналов. Наличие преобразователей кодов ПК1 и ПК2 не является обязательным в структурной схеме автомата, но в некоторых случаях их включение в схему позволяет добиться уменьшения сложности, упростить процесс построения или контроля работы схемы автомата.
Рисунок 2.3. Структурная схема с преобразователями входных и выходных сигналов
Необходимо отметить, что вид структурной схемы автомата в сильной степени зависит от используемой системы логических элементов. Например, при построении схемы на элементах с синхронизацией, сохраняющих результат логической операции до момента прихода считывающего сигнала, необходимость в элементах памяти часто отпадает. В этом случае структурная схема автомата может быть изображена в виде, приведенном на рисунке 2.3.1.
Рисунок 2.3.1. Упрощенная Структурная схема с преобразователями входных и выходных сигналов
2.4 Структурная схема на элементах импульсного типа
При построении схемы из логических элементов импульсного типа, работающих с импульсными сигналами длительностью t, и элементов памяти с выходными сигналами потенциального типа в структурную схему необходимо включить цепи синхронизации и линии задержки (ЛЗ), как это показано на рис. 4.
Рисунок 2.4. Структурная схема с линиями задержки
Линии задержки в такой схеме осуществляют задержку входных сигналов элементов памяти. Если время задержки (tз) этих линий немного больше величины t, то состояние элементов памяти остается неизменным на время действия синхронизирующего сигнала (СИ).
2.5 Основные этапы структурного синтеза
Процедуру структурного синтеза удобно рассматривать, расчленив ее предварительно на несколько связанных между собой этапов.
1. Выбор структурной схемы автомата. Этот этап синтеза во многом определяет последовательность построения схемы. Примеры того, как заданная система элементов влияет на структурную схему автомата, были приведены в предыдущем параграфе. Структурные схемы автомата, применяемые при построении схемы на потенциальных элементах, будут рассмотрены в п. 9, а структурные схемы, использующие типовые блоки, будут описаны в п. 10. Основная трудность этого этапа заключается в отсутствии формальных критериев для выбора структурной схемы. Одним из главных факторов, определяющих выбор структурной схемы, является опыт разработчика.
2. Кодирование входных и выходных сигналов. Кодирование входных сигналов заключается в том, что каждой букве pi входного алфавита абстрактного автомата однозначным образом ставится в соответствие набор значений двоичных переменных х1, х2,…, хn. Очевидно, что кодирование является однозначным, если число букв входного алфавита не превышает числа различных двоичных наборов переменных х1, х2,…, хn. Исходя из этого, количество двоичных переменных n, необходимое для кодирования r букв входного алфавита, можно определить из условия r Ј 2n. Кодирование выходных сигналов состоит в том, что буквам выходного алфавита wi абстрактного автомата аналогичным образом ставятся в соответствие наборы значений выходных переменных z1, z2,…, zm. Результаты кодирования обычно заносятся в таблицы кодирования входных и выходных сигналов.
В некоторых задачах кодирования входных и выходных сигналов задается в качестве условий работы схемы на этапе абстрактного синтеза. В таких случаях в структурную схему автомата могут быть включены преобразователи кодов. При этом кодирование заключается в том, что каждому набору значений переменных х1, х2,…, хn однозначным образом ставится в соответствие набор переменных х1', х2',…, хq', а каждому набору переменных z1, z2,…, zm – набор переменных z1', z2',…, zs'. Заметим, что в качестве преобразователей кодов на практике часто используют дешифраторы. Необходимо иметь в виду, что кодирование входных и выходных сигналов может существенно влиять на сложность комбинационной части схемы так же, как и кодирование состояний автомата.
3. Выбор числа элементов памяти и кодирование состояний автомата. Кодирование состояний заключается в том, что каждому состоянию si О S однозначным образом ставится в соответствие набор внутренних переменных у1, у2,…, уh. Состояния и соответствующие им коды обычно представляют в виде таблицы, которая называется таблицей кодирования состояний автомата.
Если автомат имеет l состояний, то, для того, чтобы получить однозначное соответствие, необходимо иметь не менее l различных двоичных кодов. Минимальное число элементов памяти, необходимое для получения однозначного кодирования, h=log2l.
Кодирование состояний существенно влияет на сложность комбинационной части схемы автомата. Для того, чтобы упростить комбинационную схему, часто используют избыточное кодирование, выбирая h большим, чем это необходимо для получения однозначного кодирования. Избыточное кодирование используется также для построения схем без состязаний. Кодирование состояний кажется целесообразным выполнять совместно с кодированием входных и выходных сигналов, однако такая задача оказывается весьма сложной и практически не реализуется.
4. Построение функций возбуждения. Функция возбуждения yi' определяет, какой сигнал нужно подать на вход i-го элемента памяти, чтобы получить код состояния, в которое автомат должен перейти. Функции возбуждения при структурном синтезе соответствуют функциям перехода абстрактного автомата. Это соответствие показывает, что функции возбуждения должны зависеть от внутренних переменных y1, y2,…, yh, определяющих состояние автомата, и входных переменных х1, х2,…, хn, относящихся к одному и тому же моменту времени. Последнее обстоятельство позволяет нам рассматривать функции возбуждения как переключательные функции:
5. Построение функции выхода. В автомате Мили каждая функция выхода zi определяет соответствующий компонент набора выходных сигналов. Функции выхода при структурном синтезе соответствуют функции выхода абстрактного автомата. Они зависят от внутренних переменных y1, y2,…, yh и входных переменных х1, х2,…, хn. Существенно, что значения переменных, определяющих zi, относятся всегда к одному и тому же моменту времени, поэтому функции выхода являются переключательными функциями:
Функции выхода автомата Мура в каждый момент времени определяют совокупность выходных сигналов:
6. Реализация функций выхода и функций возбуждения. Этот этап включает в себя действия, связанные с построением аналитического представления для переключательных функций, входящих в системы, их минимизацию, факторизацию и преобразования в операторную форму для заданной системы элементов. Заметим, что на этом этапе целесообразно также выполнять построение преобразователей кодов, которые обычно реализуются либо как система переключательных функций, либо в виде схемы «дешифратор-шифратор».
7. Графическое изображение полной схемы автомата.
2.6 Типы элементов памяти
В качестве элементов памяти на стадии структурного синтеза чаще всего используют элементарные автоматы с двумя выходными сигналами. Однако в последнее время в связи с разработкой больших интегральных схем представляет интерес использование в качестве элементов памяти широко применяемых в цифровых устройствах типовых схем: счетчиков и регистров. Элементы памяти с двумя выходными сигналами обычно называются триггерами. В большинстве случаев триггер является автоматом Мура. Он может иметь один или несколько входов. Работа триггера, как и любого автомата, описывается с помощью таблицы переходов.
На практике часто возникает задача построения триггеров из элементов заданной системы. Для этой цели используют характеристическое уравнение триггера, которое определяет состояние, в которое должен перейти триггер qt+1 в зависимости от входного сигнала xt и состояния qt, в котором находится триггер qt+1 = c (xt, qt). Построение характеристических уравнений триггеров выполняется обычно либо непосредственно по таблице переходов, либо с помощью диаграмм Вейча.
При построении функций возбуждения автомата необходимо решать обратную задачу: находить сигналы, которые нужно подать на вход триггера, чтобы перевести его из одного состояния в другое. Для этого используют матрицу переходов автомата, в которой для каждого перехода указаны соответствующие входные сигналы, вызывающие такой переход. Построение матрицы переходов выполняется, как правило, непосредственно по таблице переходов автомата.
3. Проектирование алгоритма и построение абстрактного автомата арифметико-логического устройства
3.1 Задание и исходные данные
Разработка арифметико-логического устройства, выполняющего операцию сложения и вычитания в прямом двоичном коде.
Исходные данные:
– разрядность операндов – 8 бит;
– разрядность результата – 8 бит;
– элемент памяти – ПЗУ;
– формат операндов и результата – 8 бит;
3.2 Разработка алгоритма устройства
Построим алгоритм заданного логического устройства. Распишем все возможные комбинации сочетания знаков чисел, поступающих на вход устройства с учетом типа операции
1.A+B
2.А+(-В)
3.-А+В
4.-А+(-В)
5.А-В
6.А – (-В)
7.-А-В
8.-А – (-В)
Учтя особенности сложения и вычитания в двоичном коде, получим:
А+В
А+Вд
Ад+В
Ад+Вд
А+Вд
А+В
Ад+Вд
Ад+В, где д – означает число, переведенное в дополнительный код.
Очевидно, что мы получили пары одинаковых комбинаций. Объединив номера 1 и 6, 2 и 5, 3 и 8, 4 и 7 получим:
А+В
А+Вд
Ад+В
Ад+Вд
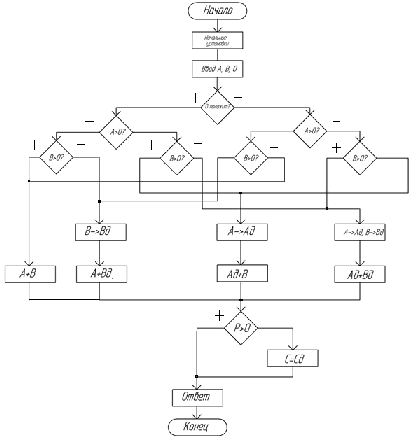
Теперь мы имеем все данные для построения алгоритма, построим его:
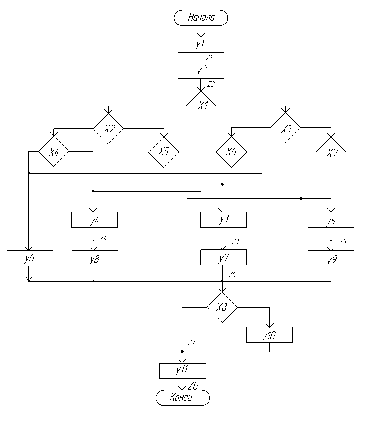
Рисунок 3.2.1. Алгоритм арифметико-логического устройства
Далее разметим алгоритм с учётом входных, выходных сигналов и состояний для построения абстрактного автомата Мили:
Рисунок 3.2.2 – Алгоритм с учётом входных, выходных сигналов и состояний
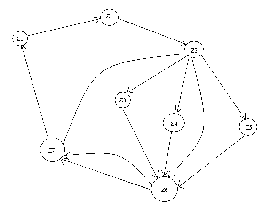
Нарисуем Граф автомата Мили
Запишем составляющие К1, К2, К3, К4, К5
К1=
К2=
К3=
К4=
К5=
Входные сигналы К1, К2, К3, К4, К5, X8,
По размеченному алгоритму построим таблицу переходов-выходов автомата Мили.
Таблица 3.2 – Таблица переходов-выходов автомата Мили
1
Z0
Z1
Z2
Z3
Z4
Z5
Z6
Z7
4. Построение функциональной и электрической принципиальной схемы
Для построения функциональной схемы с минимальными затратами входные сигналы и состояния нужно закодировать.
Табл. 4.1 – Кодировка состояний
Выходные сигналы
1
000
001
010
011
100
101
110
111
Табл. 4.2 – Кодировка выходных сигналов
Состояния
Z0
000
Z1
001
Z2
010
Z3
011
Z4
100
Z5
101
Z6
110
Z7
111
Используем таблицу 4.2 для построения шифратора
Запишем формулировки для в форме ДНФ
Теперь запишем таблицу переходов с учётом кодировок.
Табл. 4.3 – Таблица переходов-выходов автомата Мили с учётом кодировок
000
001
010
011
100
101
110
111
000
001
010
011
100
101
110
111
Используем приведенную выше таблицу для построения таблицы прошивки ПЗУ.
Табл. 4.4 – Таблица прошивки ПЗУ системы управления
Адрес
Данные
б1
б2
б3
в1
в2
в3
б1
б2
б3
y1
y2
y3
y4
y5
y6
y7
y8
y9
y10
y11
0
0
0
0
0
0
0
0
1
1
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
1
0
0
1
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
1
1
0
0
1
0
0
0
0
0
0
0
0
0
1
0
0
0
1
0
1
1
0
0
1
0
0
0
0
0
0
0
0
0
1
0
0
0
1
1
0
0
0
0
0
1
0
0
0
0
0
0
0
0
1
0
0
1
0
1
0
0
0
0
0
1
0
0
0
0
0
0
0
0
1
0
0
1
0
1
0
1
0
0
0
0
1
0
0
0
0
0
0
0
1
0
0
1
1
1
0
1
0
0
0
0
1
0
0
0
0
0
0
0
1
0
0
1
1
1
1
1
0
0
0
0
0
1
0
0
0
0
0
0
1
0
1
0
0
1
1
1
0
0
0
0
0
1
0
0
0
0
0
0
1
1
0
0
0
1
1
0
0
0
0
0
0
0
0
1
0
0
0
1
0
0
0
0
0
1
1
0
0
0
0
0
0
0
1
0
0
0
0
1
0
1
0
0
0
1
1
0
0
0
0
0
0
0
0
0
1
0
0
1
1
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
1
1
0
1
0
0
1
1
1
0
0
0
0
0
0
0
0
0
0
0
1
1
0
1
0
1
1
1
1
0
0
0
0
0
0
0
0
0
1
0
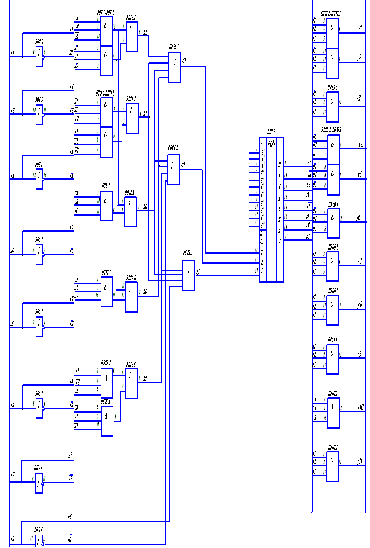
После построения функциональной схемы выбираем по справочнику элементы и строим схему электрическую принципиальную.
Выбираем следующие номиналы ИМС, присутствующие в схеме функциональной:
Так как часто в наличии и при ограничении одной серией ИМС имеется только четырех разрядный параллельный регистр, а необходим восьмиразрядный, то информационные вх./вых. двух четырех разрядных регистров включаем независимо и параллельно, а управляющие сигналы регистров необходимо соединить между собой соответственно.
Так как часто в наличии и при ограничении одной серией ИМС имеется только четырех разрядный, управляющие сигналы соединить между собой соответственно, а вывода переполнения и прибавления лог. 1 в младший разряд, соединяем таким образом. Сигнал переполнения ИМС младших разрядов соединяем с входом «прибавления лог. 1 в младший разряд» ИМС старших разрядов.
Вывод
В данном курсовом проекте была разработана система управления арифметико-логическим устройством с элементами памяти ПЗУ, выполняющее операцию сложения и вычитания в прямом двоичном коде. В процессе работы был составлен алгоритм работы устройства, абстрактный автомат Мили, таблицы прошивки ПЗУ и по ним построена система управления. В завершении работы были построены функциональная и электрическая принципиальная схемы устройства на форматах А3 и А1 соответственно. Также составлены таблицы: переходов, выходов автомата, кодирования сигналов автомата, структурную таблицу переходов, выходов и функций возбуждения.
Осуществлена реализация схемы управляющего автомата на микросхемах ТТЛ серии К555 обладающих высоким быстродействием и малым потреблением.
В ходе выполнения задания по курсовому проектированию закреплены теоретические знания по дисциплине: «цифровые автоматы».
Список источников
Глушков В.М. Синтез цифровых автоматов. М.: 1967
Самофалов К.Г. и др. Прикладная теория цифровых автоматов. К.: 1987
Савельев А.Я. Прикладная теория цифровых автоматов. М.: 1987
Справочник по интегральным микросхемам / Под ред. Б.В. Тарабрина. – М.: Энергия, 1980.
Каган Б.М., Сташин В.В. Основы проектирования микропроцессорных устройств автоматики. М.: 1987
Шило В.Л. Популярные цифровые микросхемы: Справочник. – М.: Радио и связь, 1988. – 352 с.
Зубчук В.И., Сигорский В.П., Шкуро А.Н. Справочник по цифровой схемотехнике. – К.: Техника, 1990. – 448 с.
Омельчук Н.А – Методические указания по курсовому проектированию по дисциплине «Цифровые автоматы». - Запорожье: ЗГИА, 2001. – 17 с.
Омельчук Н.А – Конспект лекций по дисциплине «Цифровые автоматы». - Запорожье: ЗГИА, 2002. – 68 с.
Глушков В.М – Синтез цифровых автоматов. - М.: 1967
Электронный справочник: Шульгин О.А., Шульгина И.Б. – Справочник по цифровым логическим микросхемам (часть 1).

Нравится материал? Поддержи автора!
Ещё документы из категории коммуникации, связь:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ