Сутність аналого-цифрових перетворювачів
Курсова робота
Сутність аналого-цифрових перетворювачів
1. Загальні відомості
Аналого-цифрові перетворювачі (АЦП) є пристроями, що приймають вхідні аналогові сигнали та генерують відповідні їм цифрові сигнали, що придатні для обробки мікропроцесорами та іншими цифровими пристроями.
Процедура аналого-цифрового перетворення безперервних сигналів у цифрову форму – є перетворення безперервної функції часу U(t), що описує вхідний сигнал у послідовність чисел {U’(tj)}, j = 0,1,2,…, що віднесені до деяких фіксованих моментів часу. Цю процедуру можна розділити на дві самостійні операції. Перша з них називається дискретизацією і є перетворенням безперервної функції часу у безперервну послідовність {U(tj)}. Друга називається квантуванням і є перетворенням безперервної послідовності у дискретну {U’(tj)}.
Найбільш поширеною формою дискретизації є рівномірна, у основі якої знаходиться теорема відліків. Згідно з цією теоремою у якості коефіцієнтів aj потрібно використовувати миттєві значення сигналу U(tj) у дискретні моменти часу tj = jt, а період дискретизації вибирати з умови
t = 1/2Fm,
де Fm – максимальна частота спектру перетворюваного сигналу.
Але спектри реальних сигналів прямують до нуля лише асимптотичне. Застосування рівномірної дискретизації до таких сигналів призводить до виникнення у системах обробки інформації специфічних високочастотних спотворень. Для уникнення таких спотворень потрібно або підвищувати частоту дискретизації, або використовувати перед АЦП фільтр нижніх частот, що звужує спектр початкового сигналу перед його аналого-цифровим перетворенням.
Для достатньо вузькосмугових сигналів операцію дискретизації можна виконати за допомогою самих АЦП та сполучити її з операцією квантування. У результаті при роботі зі змінними сигналами виникають специфічні спотворення, для оцінки яких вводять поняття апертурного часу.
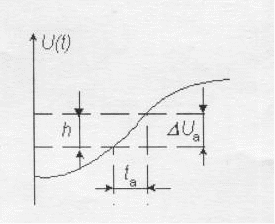
Апертурний час – час, за який зберігається невідповідність між значенням вибірки та часом, до якого вона відноситься. За апертурний час виникає амплітудна помилка, яку називають апертурною помилкою.
Звичайно для оцінки апертурної помилки використовують синусоїдальний випробувальний сигнал U(t) = Umsint, для якого максимальне відносне значення апертурної помилки
Ua/Um = ta,
як це показане на рис.1
Рис.1. Апертурна помилка
Якщо прийняти, що для N-розрядного АЦП з розділом 2-N апертурна помилка не повинна перевищувати шагу квантування, то між частотою сигналу, апертурним часом ta та відносною апертурною помилкою має місце співвідношення
1/2N = ta.
Для забезпечення дискретизації синусоїдального сигналу з частотою 100 кГц та помилкою 1% час перетворення повинен бути 25 нс. У той же час за допомогою такого АЦП можна перетворювати сигнали зі смугою частот до 20 МГц. Таким чином, дискретизація за допомогою самого АЦП призводить до суттєвого розходження між швидкодією АЦП та періодом дискретизації. Щоб позбавитись цього використовують пристрої вибірки-збереження.
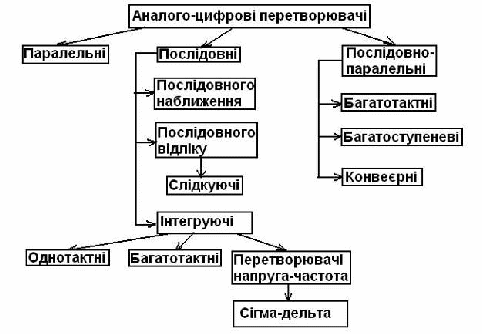
2. Класифікація аналого-цифрових перетворювачів
Ця класифікація показана на рис.2.
Рис.2. Класифікація аналого-цифрових перетворювачів
В основу класифікації покладена ознака що вказує на те, як у часі розгортається процес перетворення аналогової величини у цифрову. Операції квантування та кодування можуть здійснюватись за допомогою або послідовної, або паралельної, або послідовно-параллельної процедур наближення цифрового еквівалента до перетворюваної величини.
3. Паралельні АЦП
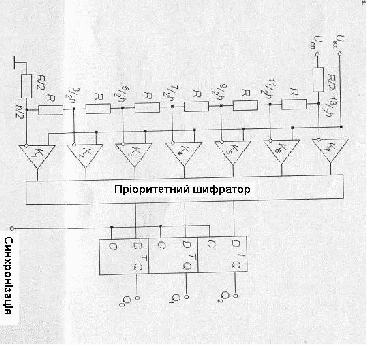
АЦП цього типу здійснюють квантування сигналів одночасно за допомогою набору компараторів, що включені паралельно джерелу вхідного сигналу. На рис.3 показана реалізація паралельного методу АЦ-перетворення для 3-розрядного числа.
За допомогою трьох війкових розрядів можна передати вісім різних чисел, включаючи нуль. Для цього потрібні сім компараторів. Сім відповідних еквідистантних опорних напруг утворюються за допомогою резистивного подільника.
Якщо прикладена вхідна напруга не виходить за межі діапазону від 5h/2 до 7h/2, де h = Uоп/7 – квант вхідної напруги, що відповідає одиниці молодшого розряду АЦП, то компаратори з 1-го по 3-й встановлюються у стан „1”, а компаратори з 4-го по 7-й – у стан „0”. Перетворення цієї групи кодів у 3-значне двійкове число виконує логічний пристрій, що називається пріоритетним шифратором.
Рис. Паралельний перетворювач для 3-розрядного числа
Діаграма стану шифратора наведена у табл.1.
Таблиця 1.
Вхідна напруга
Стан компараторів
Виходи
Uвх/h
К7
К6
К5
К4
К3
К2
К1
Q2
Q1
Q0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
1
0
0
1
2
0
0
0
0
0
1
1
0
1
0
3
0
0
0
0
1
1
1
0
1
1
4
0
0
0
1
1
1
1
1
0
0
5
0
0
1
1
1
1
1
1
0
1
6
0
1
1
1
1
1
1
1
1
0
7
1
1
1
1
1
1
1
1
1
1
Підключення приоритетного шифратора безпосередньо до виходу АЦП може призвести до похибки, якщо вхідна напруга змінюється швидко. Тому треба, щоб зміна стану компараторів проходила одночасно. Це робиться двома способами: або на вході АЦП ставлять швидкодіючий пристрів вибірки та збереження, що фіксує значення вхідної напруги, або на виході компараторів встановлюють паралельний регістр. У другому випадку використовується двотактний цикл перетворення. Завдяки одночасній роботі компараторів паралельний АЦП є найбільш швидкодіючим. Наприклад, 8-розрядний паралельний АЦП МАХ108 дозволяє довести частоту перетворення до 1,5 ГГц. Недоліком такої схеми АЦП є висока складність. Оскільки паралельний АЦП містить 2N-1 компараторів та 2N резисторів, то його вартість може бути високою (сотні доларів США). Такий АЦП має також велику споживану потужність, той самий МАХ108 споживає до 5 Вт.
4. Багатоступеневий АЦП
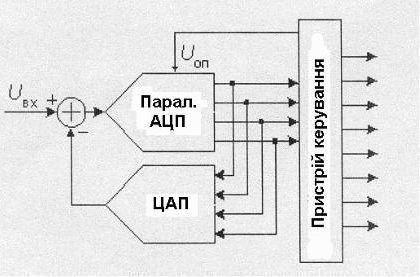
В багатоступеневому АЦП процес перетворення вхідного сигналу розділений у просторі. На рис.4 наведена схема двохступеневого 8-розрядного АЦП.
Рис.4. Двохступеневий 8-розряднй АЦП
Верхній по схемі АЦП здійснює грубе перетворення сигналу у чотири старших розряди вихідного коду. Цифрові сигнали з виходу АЦП поступають на вихідний регістр та одночасно на вхід 4-розрядного швидкодіючого цифро аналогового перетворювача (ЦАП). Різність від віднімання вихідної напруги ЦАП із вхідної напруги схеми поступає на другий АЦП (нижній по схемі). У цього АЦП опорна напруга у 16 разів менша за опорну напругу першого АЦП. Тому квант другого АЦП у 16 разів менший кванта першого АЦП. Цей залишок, що перетворений у другому АЦП у цифрову форму є чотирма молодшими розрядами. Різниця між двома АЦП в тому, що точність першого АЦП повинна бути такою, як у 8-розрядного АЦП.
Оскільки перетворення у цифрову форму здійснюється за два такти, то доцільно на вході використовувати пристрій вибірки та збереження, щоб значення вхідної напруги за час двох тактів не змінювалось.
5. Багатотактний послідовно-паралельний АЦП
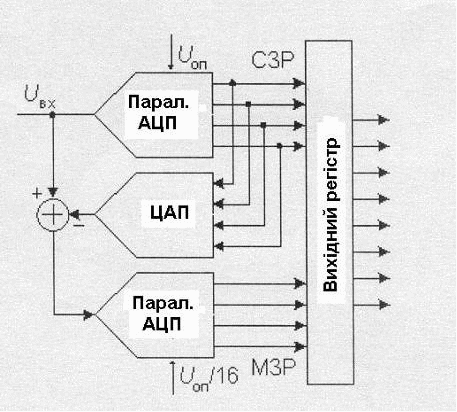
Розглянемо приклад 8-розрядного двохтактного АЦП, схема якого показана на рис.5. Процес перетворення розділений у часі.
Перетворювач складається з 4-розрядного паралельного АЦП, квант h якого визначається величиною опорної напруги, 4-розрядного ЦАП та пристрою керування. Якщо максимальний вхідний сигнал дорівнює 2,56 В, то на першому такті перетворювач працює з шагом квантування h1=0,16 В. В цей час вхідний код ЦАП дорівнює нулю.
Рис.5. Двохтактний 8-розрядний АЦП
Пристрій керування передає одержане на першому такті слово у чотири старших розряди вихідного регістру, подає це слово на вхід ЦАП та зменшує у 16 разів опорну напругу АЦП. Таким чином, у другому такті шаг квантування h2=0,01 В і залишок, що з’явився при відніманні з вхідної напруги вихідної напруги ЦАП, буде перетворений у молодший полу байт вихідного слова.
Використовувані у цій схемі 4-розрядні АЦП та ЦАП повинні мати 8-розрядну точність, інакше можливий пропуск кодів. Як і у попереднього АЦП на вході потрібно встановлювати пристрій вибірки та збереження.
Прикладом такого АЦП є трьохтактний 12-розрядний AD7886 з часом перетворення 1 мкс.
6. Конвеєрний АЦП
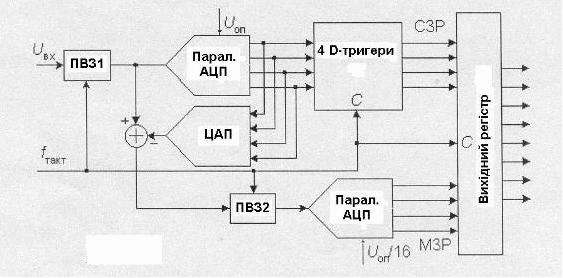
Швидкодію багатоступеневого АЦП можна підвищити за допомогою конвеєрного принципу багатоступеневої обробки. У звичайному багатоступеневому АЦП рис.4 спочатку формуються старші розряди вихідного слова першим АЦП, потім іде встановлення вихідного сигналу ЦАП. На цьому інтервалі другий АЦП простоює. Тому треба ввести елементи затримки між першою та другою ступенями і одержимо конвеєрний АЦП, схема якого показана на рис.6.
Рис.6. Конвеєрний АЦП
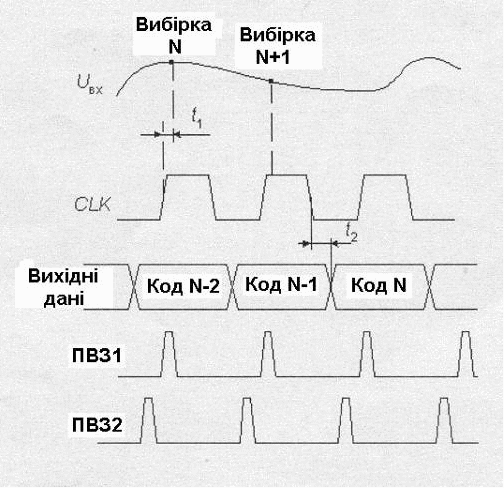
Роль аналогового елемента затримки виконує пристрій вибірки та збереження ПВЗ2, а цифрового – чотири D-тригери. .Ці тригери затримують передачу старшого полу байту у вихідний регістр на один період тактового сигналу.
Сигнали вибірки, що формуються з тактового сигналу, поступають на ПВЗ1 та ПВЗ2 у різні моменти часу (рис.7).
Рис.7. Діаграма вибірок конвеєрного АЦП
ПВЗ2 переходить у режим збереження пізніше, ніж ПВЗ1 на час, що дорівнює сумарній затримці розповсюдження сигналу по АЦП1 та ЦАП. Задній фронт тактового сигналу керує записом кодів в D - тригери та вихідний регістр. Повна обробка вхідного сигналу займає біля двох періодів тактових імпульсів CLK, але частота появлення нових значень вихідного коду дорівнює частоті тактового сигналу. Таким чином, конвеєрна архітектура дозволяє суттєво (в декілька разів) збільшити максимальну частоту вибірок багатоступеневого АЦП. Те, що при цьому зберігається сумарна затримка проходження сигналу, що відповідає звичайному багатоступеневому АЦП з такою ж кількістю ступенів, не має суттєвого значення, так як час наступної цифрової обробки цих сигналів все одно набагато більше цієї затримки. За рахунок цього можна без програшу у швидкодії збільшити кількість ступенів АЦП, зменшивши розрядність кожної ступені. В свою чергу, збільшення числа ступенів перетворення зменшує складність АЦП. Дійсно, наприклад, для побудови 12-розрядного АЦП з чотирьох 3-розрядних потрібно 28 компараторів, тоді як його реалізація з двох 6-розрядних потребує 126 компараторів.
Конвеєрну структуру має багато АЦП, що виготовляються зараз. Так двохступеневий 10-розрядний AD9040 виконує до 40 мільйонів перетворень за секунду, 12-розрядний AD9220 виконує до 10 мільйонів перетворень за секунду. При роботі з конвеєрним АЦП треба знати, що багато з них не допускають низьких частот вибірок, бо внутрішні ПВЗ мають велику швидкість розряду конденсаторів.
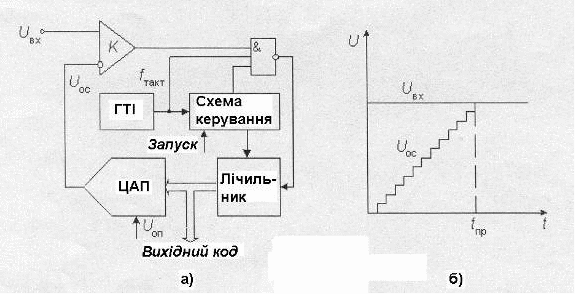
7. АЦП послідовного лічіння
Цей АЦП складається з компаратора, лічильника та ЦАП (рис.8). На один вхід компаратора поступає вхідний сигнал, на інший – сигнал зворотного зв’язку з ЦАП.
Рис.8. а) схема АЦП послідовного лічення; б) діаграма роботи.
Робота перетворювача починається з приходу імпульсу запуску, який включає лічильник, що сумує кількість імпульсів, що поступають від генератора тактових імпульсів ГТІ. Вихідний код лічильника подається на ЦАП, що перетворює цей код у напругу зворотного зв’язку Uос. Процес перетворення продовжується доки напруга зворотного зв’язку не стане рівним до вхідної напруги, тоді переключиться компаратор, який своїм вихідним сигналом припиняє доступ тактових імпульсів на лічильник. Перехід виходу компаратора з „1” в „0” означає закінчення процесу перетворення. Вихідний код, пропорційний вхідній напрузі в момент закінчення перетворення, зчитується з виходу лічильника.
Час перетворення АЦП цього типу є змінним и визначається вхідною напругою. При розрядності війкового лічильника N та частоті тактових імпульсів fтакт дорівнює
Tпер = (2N – 1)/такт.
Наприклад, при N=10 та fтакт = 1 МГц Tпер = 1024 мкс, що забезпечує максимальну частоту вибірок біля 1 кГц.
АЦП цього типа без пристрою вибірки та збереження можуть працювати тільки з постійними та повільно змінними напругами, що змінюються на величину не більшу за квант перетворення за час перетворення.
Таким чином недоліком АЦП такого типу є повільне перетворення, а позитивна якість – простота побудови.
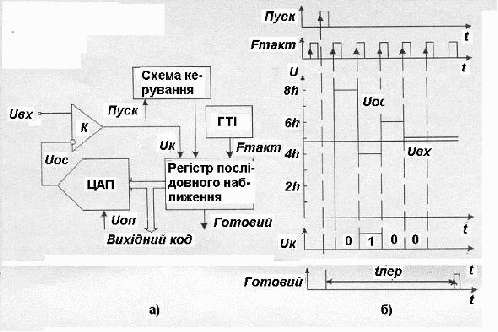
8. АЦП послідовного наближення
Перетворювач цього типу, що в літературі називається також АЦП з послідовним порівнянням – найбільш розповсюджений варіант послідовного АЦП.
В основі роботи цього класу АЦП полягає принцип послідовного порівняння вхідної напруги з ½, ¼, 1/8 і т.і. від можливого максимального значення вхідної напруги. Це дозволяє для N-розрядного АЦП послідовного наближення виконати увесь процес перетворення за N послідовних ітерацій замість 2N – 1 при використанні послідовного лічиння і одержати суттєвий виграш у швидкодії. Так, вже при N=10 цей виграш досягає 100 разів і дозволяє одержати за допомогою таких АЦП до 105...106 перетворень за секунду. У той же час статична похибка перетворювачів цього типу, що залежить від використаного ЦАП, може бути дуже малою, що дозволяє реалізувати роздільну здатність до 18 двійкових розрядів при частоті вибірок до 200 кГц (наприклад, DSP101 фірми Burr-Brown). На рис.9а показана структура 4-розрядного перетворювача, який складається з трьох головних вузлів: компаратора (К), регістра послідовного наближення та ЦАП. На рис.9б показана діаграма роботи цього перетворювача.
Рис.9. а) структура АЦП послідовного наближення; б) діаграма роботи АЦП послідовного наближення.
Після подачі команди „Пуск” з приходом першого тактового імпульсу регістр послідовного наближення (РПН) примусово задає на вхід ЦАП код, що дорівнює половині його шкали (для 4-розрядного ЦАП це 1000). завдяки цьому напруга Uос стає рівною 8h, де h – квант вихідної напруги ЦАП, що відповідає одиниці молодшого розряду. Ця величина складає половину діапазону вхідного сигналу. Якщо вхідна напруга більша, ніж ця величина, то на виході компаратора встановлюється „1”, якщо менша, то „0”. У цьому випадку схема керування повинна переключити старший розряд d3 знову у стан „0”. Після цього залишок Uвх – d3*8h таким же чином порівнюється з найближчим молодшим розрядом і т.і. Після чотирьох подібних шагів в РПН визначається війкове число, з якого після цифро-аналогового перетворення утворюється напруга, що відповідає Uвх з точністю до одиниці молодшого розряду. Вихідне число може бути зчитане з РПН у вигляді паралельного двійкового коду по N лініям.
Швидкодія такого АЦП визначається сумою часу встановлення ЦАП, часу переключення компаратору та затримкою розповсюдження сигналу в РПН. Для ефективного використання такого АЦП вхідну напругу треба підключати через пристрій вибірки та збереження (ПВЗ). Більшість таких АЦП мають ПВЗ у своєму складі, наприклад 16-розрядний AD7882.
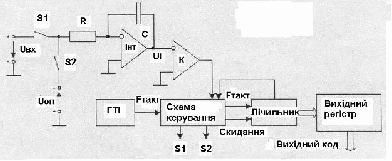
9. АЦП багатократного інтегрування
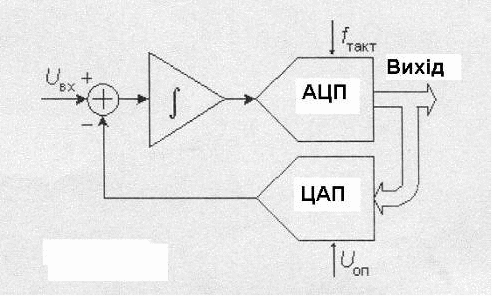
Ті АЦП, що були розглянуті раніше, мають малу перешкодоздатність, тому що вхідна напруга звичайно включає у себе перешкоди. В інтегруючих АЦП вхідний сигнал інтегрується, що дозволяє уникнути перешкод. На рис.10 показана спрощена схема АЦП, що працює у два такти.
Рис.10. АЦП багатократного інтегрування
Перший такт – інтегрування, другий такт – лічення. На початку першої стадії ключ S1 замкнений, а ключ S2 – розімкнений. Інтегратор Інт інтегрує вхідну напругу Uвх. Час інтегрування вхідної напруги постійний t1, у якості таймера використовується лічильник з коефіцієнтом лічення Кл, тому t1 = Кл/Fтакт.
До моменту закінчення ліку вихідна напруга інтегратора складає:
Ui = 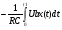 = - Uвх.сер Кл/FтактRC,
= - Uвх.сер Кл/FтактRC,
де Uвх.сер – середня вхідна напруга за час t1. Після закінчення стадії інтегрування ключ S1 розмикається, а ключ S2 замикається і опорна напруга Uоп подається на вхід інтегратора.
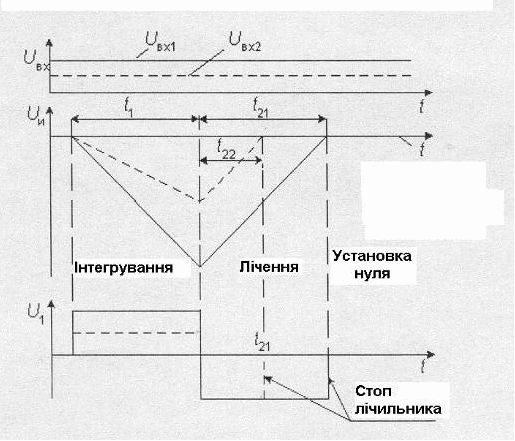
При цьому вибирається опорна напруга протилежна за знаком вхідній напрузі. На стадії лічення вихідна напруга інтегратора лінійно зменшується, як це показане на рис.11.
Стадія лічення закінчується, коли вихідна напруга інтегратора переходить через нуль. При цьому компаратор К перемикається і лічення зупиняється. Інтервал часу, на якому іде стадія лікування, визначається рівнянням:
Ui(t1) + 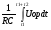 = 0.
= 0.
Рис.11. Діаграма роботи АЦП багатократного інтегрування
Якщо підставити значення Ui з урахуванням того, що t2 = n2/Fтакт, де n2 – зміст лічильника після закінчення стадії лічення, то одержимо:
n2 = Uвх.сер Кл/Uоп.
З цієї формули виходить, що особливістю методу багатократного інтегрування, що ні тактова частота, ні постійна інтегрування RC не впливають на результат. Необхідно тільки, щоб тактова частота на інтервалі часу t1 + t2 залишалась постійною. Це можна забезпечити при використанні простого генератора тактової частоти (ГТІ), оскільки дрейф його частоти проходить за час забагато більший, ніж час перетворення.
У всі математичні вирази, що наведені вище, входить не миттєве значення напруги, а значення, усереднене за час t1. тому, чим вище частота перешкоди, тим більше ослаблення перешкоди.
10.Перетворювачі напруга–частота
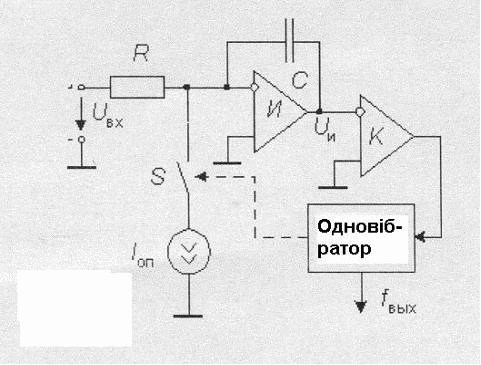
На базі перетворювачів напруга-частота (ПНЧ) можуть бути побудовані інтегруючі АЦП, що забезпечують високу точність перетворення. Існує декілька типів ПНЧ. Найбільше застосування одержали ПНЧ з заданою тривалістю вихідного імпульсу. Структурна схема такого ПНЧ наведена на рис.12. По цій схемі побудована вітчизняна мікросхема КР1108 ПП1.
Під дією позитивного вхідного сигналу Uвх напруга Uи на виході інтегратора И зменшується. При цьому ключ S розімкнений. Коли напруга Uи зменшується до нуля, компаратор К перемикається та запускає одновібратор. Той формує імпульс стабільної тривалості Ти, який керує ключем. Послідовність цих імпульсів є вихідним сигналом ПНЧ. Ключ замикається, струм Іоп на протязі Ти поступає на вхід інтегратору, призводячи до збільшення вихідної напруги інтегратору. Далі процес повторюється.
Рис.12. Схема перетворювача напруга-частота
Імпульси струму Іоп зрівноважують струм, що викликається вхідною напругою Uвх. У сталому режимі
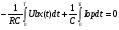 .
.
Звідки: f = 1/T = Uвх.сер/RIопТи,
де Uвх.сер – середнє значення вхідної напруги за період Т.
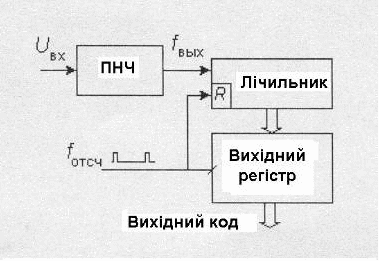
Цей вираз показує, що точність перетворення визначається точністю установки опорного струму Іоп, точністю витримки тривалості імпульсу одно вібратора Ти, а також точністю резистора R. Ємність інтегратора на впливає на частоту ПНЧ. таким чином, ПНЧ перетворює вхідну напругу в унітарний код. Для його перетворення у двійковий позиційний можна використовувати лічильник. Схема інтегруючого АЦП на базі ПНЧ наведена на рис.1
Рис.1 Схема інтегруючого АЦП на базі ПНЧ
Двійковий лічильник підраховує кількість імпульсів, що поступила від ПНЧ за період Твідл = 1/fвідл, що задається відліковими імпульсами. котрими вміст лічильника заноситься у вихідний регістр. За цим проводиться скидання лічильника. Кількість імпульсів n, що підраховані лічильником за час Твідл:
n = Т відл Uвх сер./Ти RIоп.
Тут Uвх.сер – середнє значення вхідної напруги за увесь період Твідл.
Можна помітно підвищити точність ПНЧ, якщо замість одновібратору підключити D-трігер, що тактується імпульсами стабільної частоти.
11. Сігма-дельта АЦП
АЦП багатократного інтегрування мають багато недоліків. По-перше нелінійність перехідної статичної характеристики операційного підсилювача, на якому зроблений інтегратор, помітно визначається на характеристиці перетворення АЦП з високим розділенням. Для зменшення впливу цього фактору АЦП виготовляють багатоактними. Наприклад 13-розрядний AD7550 виконує перетворення у 4 такти. Іншим недоліком цих АЦП є та обставина, що інтегрування вхідного сигналу займає у циклі перетворення тільки приблизно третину. Дві третини циклу перетворювач не приймає вхідний сигнал. Це погіршує властивості АЦП щодо придушення спотворень. По-третє АЦП багатотактного перетворення повинен мати досить багато наріжних резисторів та конденсаторів з високоякісним діелектриком, що значно збільшує місце, що займає перетворювач на платі.
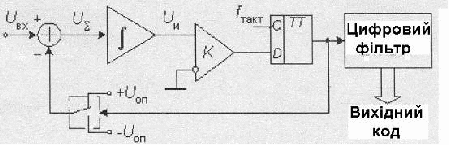
Ці недоліки усунуті у сигма-дельта АЦП. У цих АЦП є два головних блоки: суматор та інтегратор. Один з принципів у цих перетворювачах, що дозволяє зменшити погрішність, що вноситься спотвореннями – це усереднення результатів вимірів на великому інтервалі часу.
Головні вузли АЦП – сігма-дельта модулятор та цифровий фільтр. Схема N- розрядного сігма-дельта модулятора першого порядку наведена на рис.14.
Рис.14. Сігма-дельта модулятор першого порядку
Робота цієї схеми заснована на відніманні з вхідного сигналу Uвх(t) величини сигналу на виході ЦАП, що здійснена а попередньому такті роботи схеми. Одержана різниця інтегрується, а потім перетворюється у код паралельним АЦП невеликої розрядності. Послідовність кодів поступає на цифровий фільтр нижніх частот.
Порядок модулятора визначається кількістю інтеграторів та суматорів в його схемі. Сігма-дельта модулятори N-го порядку мають N суматорів та N інтеграторів та забезпечують більше співвідношення сигнал-спотворення при тій же частоті відліків, що і модулятори першого порядку. Прикладами сігма-дельта модуляторів високого порядку є одноканальний AD7720 сьомого порядку. Найбільш широко у складі інтегральних мікросхем використовуються однобітні сігма-дельта модулятори, в яких у якості АЦП використовується компаратор, а в якості ЦАП – аналоговий комутатор – рис.15.
Рис.15. Сігма-дельта АЦП першого порядку
На відміну від АЦП з перетворювачами напруга – частота сігма-дельта модулятор синхронізований тактовою частотою fтакт. Вихідний сігма-дельта модульований сигнал є послідовність одиничних та нульових посилок, тривалість яких = 1/fтакт, а загальна частота – fтакт. При цьому частота одиничних посилок є частотою модулятора і пропорційна модулюючому аналоговому сигналу.
Частота тактових імпульсів вибирається з розрахунку fтакт = fдКдец, де Кдец – коефіцієнт децимації, зниження частоти відліків до значення частоти дискретизації fд при наступному цифровому перетворенні. В найпростішому випадку Кдец = 2N, де N – розрядність формованого цифрового сигналу. Згідно з теоремою Котельникова, для дискретизованого сигналу з верхньою частотою спектру fc повинна виконуватись умова fc < fд/2. Ця умова розповсюджується не тільки на корисний сигнал, але і на супроводжуючі його спотворення. Тому на вході звичайних АЦП встановлюють фільтр нижніх частот.
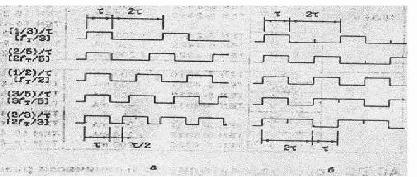
Для сігма-дельта модулятора тактова частота fт є частотою дискретизації його вхідного сигналу. Оскільки fт в Кдец разів більша за fд, її називають частотою збиткової дискретизації (oversampling). На рис.16 показані епюри напруг звичайного перетворення напруги у частоту (а), і перетворення у сігма-дельта модуляторі (б).
Рис.16. Епюри напруг: а) перетворення напруги в частоту; б) перетворення у сігма-дельта модуляторі
Імпульси при звичайній модуляції мають постійну тривалість, а сігма-дельта - змінну, але кратну = 1/fт (складаються з одиничних посилок). Зліва на рис.16 записані значення частот проходження імпульсів перетворення у частоту та одиничних посилок сігма-дельта модулятора, що виражені через через . Справа на рис.16 показана та ж сама послідовність, але синхронізована. Таким чином, сігма-дельта- модульований сигнал це частотно-модульована послідовність одиничних імпульсів, частота яких пропорційна сумі сигналу та шуму синхронізації.
На сьогодні сігма-дельта АЦП – єдині, які можуть виконати 24-розрядне перетворення аналогового сигналу.
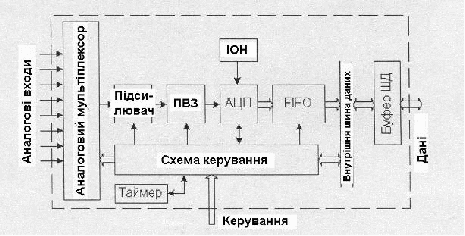
12. Системи збирання даних та мікроконвертори
Зараз розповсюджені АЦП, де дані сприймаються з багатьох джерел. Такі АЦП називаються системами збирання даних (data acquisition system) або мікроконверторами. Функціональна схема мікроконвертора наведена на рис.17.
Рис.17. Функціональна схема мікроконвертора
Основу цієї системи складає АЦП, звичайно АЦП послідовного наближення. Щоб зменшити кількість корпусів інтегральних мікросхем, що потрібні для системи збору даних, у схему вмонтовані ПВЗ та джерело постійного живлення, Для підключення до декількох джерел вхідних аналогових сигналів використовується аналоговий мультіплексор. Щоб зменшити частоту переривань головного процесора деякі системи збору даних мають оперативні запам’ятовуючі пристрої типу FIFO (First In – First Out – першим увійшов – першим вийшов). Вимірювальний підсилювач, що входить у систему, змінює свій коефіцієнт підсилення по команді зі схеми керування. Це дозволяє вирівняти діапазони аналогових сигналів з різних входів. Схема керування може включати до себе оперативний запам’ятовуючий пристрій, в який завантажується від головного процессору блок робочих команд. В систему збирання даних вбудовується цифровий таймер, який визначає темп перетворення АЦП.
Характерним прикладом системи збирання даних є AD7581 (вітчизняний аналог 572ПВ4), що містить 8-входовий аналоговий мультиплексор, 8-розрядний АЦП послідовного наближення та запам’ятовуючий пристрій.
Особий клас пристроїв з АЦП – це мікроконвертори. Analog Devices створила прилади програмовані пристрої, що вміщували багатоканальний АЦП, мікро контролер та одно- або двохканальний ЦАП. Такий мікро конвертор приймає аналогові сигнали, перетворює їх у цифрові коди, по програмі мікроконтролера перетворює ці коди та за допомогою ЦАП знову перетворює їх у аналогові сигнали. Мікроконвертор ADuC812 має 8-канальний мультіплексор, ПВЗ, 12-розоядний АЦП послідовного наближення з швидкодією 200 кіловибірок за секунду, 2 12-розрядні ЦАП та мікроконтролер.
13. Інтерфейси АЦП
Цифровий інтерфейс – система, що забезпечує зв’язок АЦП з приймачами цифрових сигналів. Структура цифрового інтерфейсу визначає спосіб підключення АЦП до приймача цифрового коду, зокрема мікропроцесора, або цифрового процесора сигналів.
Найбільш часто використовують спосіб зв’язку АЦП з процесором, при якому АЦП є для процесора як би однією з комірок пам’яті. При цьому АЦП має необхідне число адресних входів, дешифратор адреси і підключається безпосередньо до адресної шини та шині даних процесора. Для цього він повинен обов’язково мати вихідні каскади з трьома станами.
Інша умова спільної роботи АЦП з мікропроцесорами, що називається програмним сполученням, є спільним для будь-яких систем, в які входять ЕОМ та АЦП. Є декілька способів програмного сполучення АЦП з процесорами. Розглянемо головні.
Перевірка сигналу перетворення
Цей спосіб полягає в тому, що команда початку перетворення „Пуск” періодично подається на АЦП від таймера. Процесор знаходиться у режимі очікування від АЦП сигналу перетворення „Готовий”, після якого виходить з циклу, зчитує дані з АЦП та переходить або до слідую чого перетворення, або до виконання головної програми. Тут АЦП виступає як ведучий пристрій (master), а процесор – як відомий (slave). Цей спосіб майже не потребує додаткової апаратури, але він придатний лише в системах, де процесор не дуже завантажений. Цей спосіб дозволяє максимально використовувати продуктивність АЦП. Якщо тривалість обробки даних від АЦП помітно більше, ніж час перетворення АЦП, можна використовувати варіант цього способу, що відрізняється тим, що сигнал „Пуск” поступає від процесора. Процесор виконує головну програму обробки даних, а потім зчитує дані з АЦП та знову його запускає. У цьому випадку процесор виступає у ролі ведучого пристрою, а АЦП – відомого.
Просте переривання
Видавши команду „Пуск”, процесор продовжує роботу по головній програмі. Після закінчення перетворення формується сигнал переривання, який перериває у процесорі обчислення і включає процедуру пошуку периферійного приладу, що надіслав команду переривання. Ця процедура полягає у переборі усіх периферійних пристроїв доки не буде знайдений потрібний. Перевага цього способу у порівнянні з попереднім – більша кількість перетворень за один і той же час, якщо АЦП працює повільно. Якщо АЦП – швидкий, то цей спосіб може виявитись навіть повільнішим, ніж попередній, тому що на обробку переривання може знадобитись значний час.
Векторне переривання
Цей спосіб відрізняється від попереднього тим, що разом із сигналом переривання надсилається також адрес програми звернення до даного АЦП. Тому не треба перебирати усі периферійні прилади.
Прямий доступ до пам’яті
Тут також використовується переривання, але на відміну від попередніх двох способів керування по системі переривання передається на спеціальний інтерфейс, який виконує перезапис даних перетворення у пам’ять, минаючі регістри процесора. Це дозволяє скоротити тривалість переривання до одного такту. Номери комірок пам’яті зберігаються у адресному регістрі інтерфейсу.
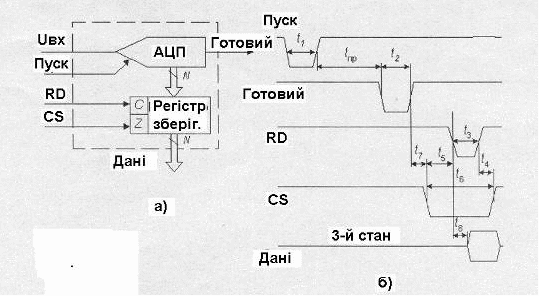
АЦП з паралельним інтерфейсом вихідних даних
У найпростіших випадках інтерфейс здійснюється за допомогою N-розрядного регістру збереження, що має три стану виходу. На рис.18 показана функціональна схема такого АЦП та часові діаграми роботи інтерфейсу.
Рис.18. а) функціональна схема паралельного інтерфейсу; б) часові діаграми роботи.
На зростаючому вході сигналу „Пуск” ПВЗ перетворювача переходить у режим та починається процес перетворення. Коли перетворення закінчується, на вихідну лінію „Готовий” виводиться імпульс, що показує на те, що у вихідному регістрі АЦП знаходиться новий результат. Сигнали CS (вибір кристалу) та RD (читання) керують виводом даних для передачі приймачу.
АЦП з послідовним інтерфейсом вихідних даних
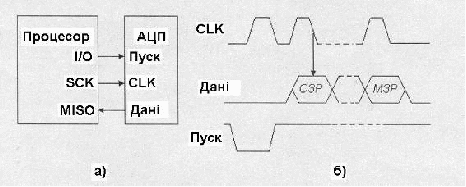
В АЦП послідовного наближення вихідна величина може бути зчитана у вигляді послідовного коду прямо з регістру. На рис.19 показана функціональна схема такого інтерфейсу (а) та часові діаграми його роботи (б).
Рис.19. а) функціональна схема послідовного інтерфейсу; б) часові діаграми його роботи.
Це схема SPI-інтерфейсу. Процесор є ведучим (master). Він ініціює початок процесу перетворення початком імпульсу „Пуск”. З тактового виходу процесора на вхід CLK АЦП поступає послідовність тактових імпульсів. Починаючи з другого такту після пуску на виході даних АЦП формується послідовний код вихідного слова старшими бітами наперед. Цей сигнал поступає на MISO (master – input (вхід), slave – output (вихід).
14. Параметри АЦП
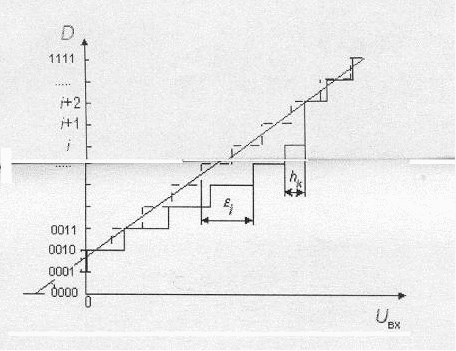
При послідовному зростанні значень вхідного аналогового сигналу Uвх(t) від 0 до величини, що відповідає повній шкалі АЦП Uпш вихідний цифровий сигнал D(t) створює ступеневу кусочно-постійну лінію. Таку залежність називають характеристикою перетворення АЦП. На рис.20 показана статична характеристика перетворення АЦП.
Рис.20. Статична характеристика перетворення АЦП
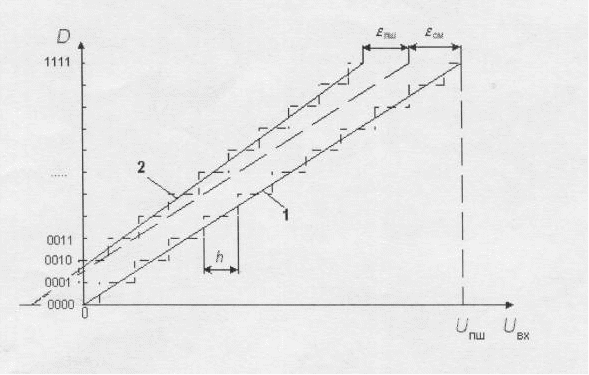
У відсутності апаратних погрішностей середні точки ступенів розташовані на ідеальній прямій 1, якій відповідає ідеальна характеристика перетворення. Реальна характеристика може суттєво відрізнятись від ідеальної розмірами та формою ступенів, а також Ії розміщенням на площині координат. Для кількісного опису цих відмінностей є цілий ряд параметрів.
Статичні параметри
Роздільна здатність – величина, що є зворотною максимальній кількості кодових комбінацій на виході АЦП. Вона виражається у процентах, розрядах або децибелах і характеризує потенційні можливості АЦП з точки зору точності. Наприклад, 12-розрядний АЦП має роздільну здатність 1/4096 або 0,0245% від повної шкали.
Роздільній здатності відповідає приріст вхідної напруги АЦП Uвх при зміні Dj на одиницю молодшого розряду. Цей приріст є шагом квантування (ОМР). Чим більша розрядність перетворювача, тим вища його роздільна здатність.
Погрішність повної шкали – відносна різниця між реальним та ідеальним значеннями межі шкали перетворення при відсутності зміщення нуля.
ПШ = ПШ100%/Uпш.
Ця погрішність є мультиплікативною складовою повної погрішності.
Погрішність зміщення нуля – значення Uвх, коли вхідний код ЦАП дорівнює нулю. Є адитивною складовою повної погрішності. Звичайно визначається по формулі
СМ = Uвх01 – h/2,
де Uвх01 – значення вхідної напруги, при якому відбувається перехід вихідного коду з 0 до 1. Часто визначається в мілівольтах або процентах від повної шкали
СМ = СМ100%/Uпш.
Погрішність повної шкали та зміщення нуля можуть бути зменшені або настроюванням аналогової частини схеми, або корекцією обчислювального алгоритму цифрової частини пристрою.
Погрішністі лінійності характеристики перетворення не можуть бути усунені такими простими засобами. тому вони є найважливішими метрологічними характеристиками АЦП.
Нелінійність – максимальне відхилення реальної характеристики перетворенняD(Uвх) від оптимальної (лінія 2 на рис.20). Оптимальна характеристика знаходиться емпірично так, щоб мінімізувати значення погрішності нелінійності. Нелінійність звичайно визначається у відносних одиницях, але у довідникових даних наводиться також у ОМР. Для характеристики, наведеної на рис.21
Л = j100%/Uпш.
Рис.21. Визначення нелінійності
Диференційною нелінійністю АЦП в даній точці характеристики перетворення називається різниця між значенням кванту перетворення hk і середнім значенням кванту перетворення h. У специфікаціях на конкретні АЦП значення диференційної нелінійності наводяться у долях ОМР або процентах від повної шкали. Для характеристики, наведеної на рис.21:
Л = (hk – h)100%/Uпш.
Погрішність диференційної нелінійності визначає дві важливих властивості АЦП: відсутність зникання кодів та монотонність характеристики перетворення. Відсутність зникання кодів – властивість АЦП видавати усі можливі вихідні коди при зміні вхідної напруги від початкової до кінцевої точок діапазону перетворення. Приклад зникання коду j+1 показаний на рис.21.
Монотонність характеристики перетворення – незмінюваність знаку приросту вихідного коду D при монотонній зміні вхідного перетворюваного сигналу. Монотонність не гарантує малих значень диференційної нелінійності та відсутності зникнення кодів.
Температурна нестабільність АЦП характеризується температурними коефіцієнтами погрішності повної шкали та погрішності зміщення нуля.
Динамічні параметри
Максимальна частота дискретизації (перетворення) – найбільша частота, з якою відбувається формування вибіркових значень сигналу, при яких вибраний параметр АЦП не виходить за задані границі. Вимірюється як число вибірок за секунду.
Час перетворення (tпр) – час від початку імпульсу дискретизації або початку перетворення до появи на виході АЦП сталого коду, що відповідає даній виборці.
Час вибірки (стробування) –час, за який відбувається виникнення одного вибіркового значення.
Шуми АЦП
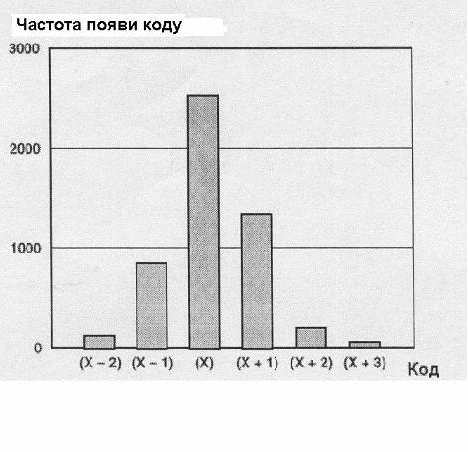
В ідеальному випадку перетворення постійного вхідного сигналу повинні давати один і той же цифровий код. Однак, внаслідок неминучого шуму у схемах АЦП існує діапазон вихідних кодів для заданої напруги на вході. якщо подати на вхід АЦП постійний сигнал та записати велику кількість перетворень, то одержимо деякий розподіл кодів. Наприклад, на рис.22 наведена гістограма результатів 5000 перетворень постійного вихідного сигналу, що виконана 16-розрядним АЦП AD7884.
Рис.22. Гістограма результатів перетворень постійного вхідного сигналу

Нравится материал? Поддержи автора!
Ещё документы из категории коммуникации, связь:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ