Типовые динамические звенья и их характеристики
























































































































































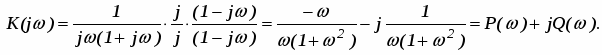
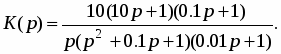
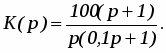
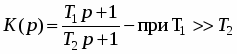
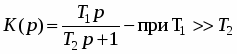
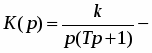

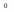
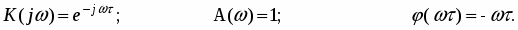
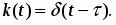
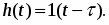
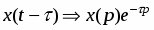
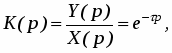
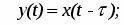
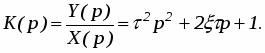
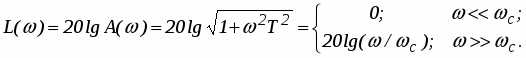
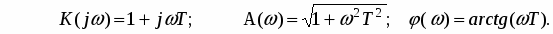
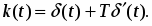
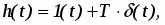
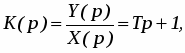
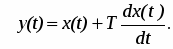
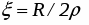
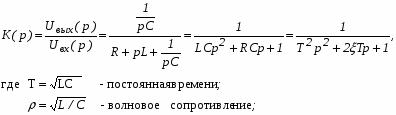

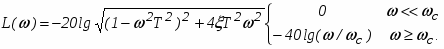
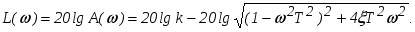
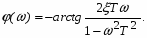
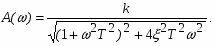
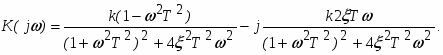
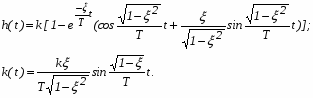
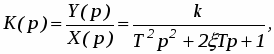
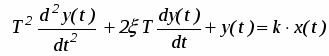
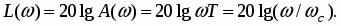
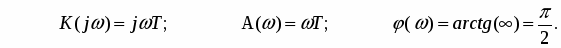
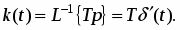
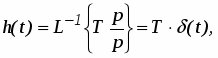
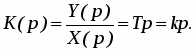
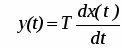
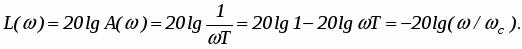
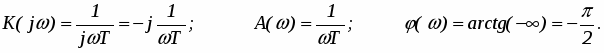
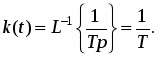
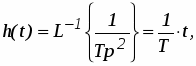
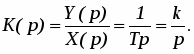
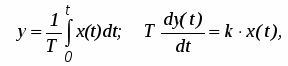
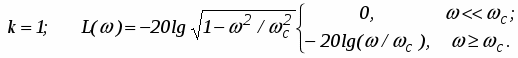
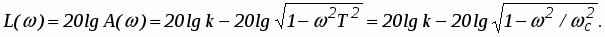
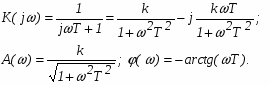
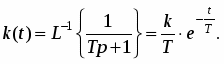
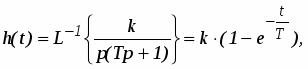
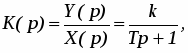
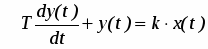
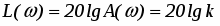
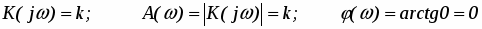
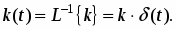
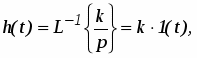
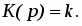
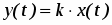
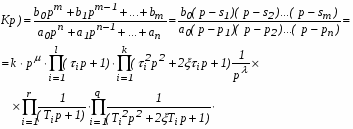
Типовые динамические звенья и их характеристики
Динамическим звеном называется элемент системы, обладающий определенными динамическими свойствами.
Любую систему можно представить в виде ограниченного набора типовых элементарных звеньев, которые могут быть любой природы, конструкции и назначения. Передаточную функцию любой системы можно представить в виде дробно-рациональной функции:
(1)
Таким образом, передаточную функцию любой системы можно представить как произведение простых множителей и простых дробей. Звенья, передаточные функции которых имеют вид простых множителей или простых дробей, называют типовыми или элементарными звеньями. Типовые звенья различаются по виду их передаточной функции, определяющей их статические и динамические свойства.
Как видно из разложения, можно выделить следующие звенья:
Усилительное (безынерционное).
Дифференцирующее.
Форсирующее звено 1-го порядка.
Форсирующее звено 2-го порядка.
Интегрирующее.
Апериодическое (инерционное).
Колебательное.
Запаздывающее.
При исследовании систем автоматического управления она представляется в виде совокупности элементов не по их функциональному назначению или физической природе, а по их динамическим свойствам. Для построения систем управления необходимо знание характеристик типовых звеньев. Основными характеристиками звеньев являются дифференциальное уравнение и передаточная функция.
Рассмотрим основные звенья и их характеристики.
Усилительное звено (безынерционное, пропорциональное). Усилительным называют звено, которое описывается уравнением:
(2)
или передаточной функцией:
(3)
При этом переходная функция усилительного звена (рис. 1а) и его фун-кция веса (рис. 1б) соответственно имеют вид:
t
t
0
h(t)
0
k.1(t)
k(t)
k.(t)
а) б)
Рис. 1
Частотные характеристики звена (рис. 2) можно получить по его передаточной функции, при этом АФХ, АЧХ и ФЧХ определяются следующими соотношениями:
.
+j
k +
АФХ
АЧХ
ФЧХ
0
0
k
0
0
0
()
A()
h(t)
Рис. 2
Логарифмическая частотная характеристика усилительного звена (рис. 3) определяются соотношением .
L()
k<1
0
k>1
k=1
ЛАЧХ
Рис. 3
Примеры звена:
Усилители, например, постоянного тока (рис. 4а).
Потенциометр (рис. 4б).
Uвых
Uвх
R
Roc
Rвх
Uвых
Uвх
а) б)
Рис. 4
3. Редуктор (рис. 5).
K(p)=i=вых /вх.
вх
Рис. 5
Апериодическое (инерционное) звено. Апериодическим называют звено, которое описывается уравнением:
(4)
или передаточной функцией:
(5)
где Т – постоянная времени звена, которая характеризует его инерционность, k – коэффициент передачи.
При этом переходная функция апериодического звена (рис. 6а) и его функция веса (рис. 6б) соответственно имеют вид:
h(t) k1(t) 0 t T а)
k/T
0 t б)
Рис. 6
Частотные характеристики апериодического звена (рис. 7а-в) опреде-ляются соотношениями:
-/4
-/2
k/2 k +
ФЧХ
0
0
()
c=1/T
+j
АФХ
c = 1/T
k
k
2
АЧХ
0
0
A()
c =1/T
-k/2
h(t)
а) б) в)
Рис. 7
Логарифмические частотные характеристики звена (рис. 8) определяются по формуле
При
+20
0
-20
ЛАЧХ
L()
-20 дБ/дек
с
0.1 1 10 100
Рис. 8
Это асимптотические логарифмические характеристики, истинная характеристика совпадает с ней в области больших и малых частот, а максимальная погрешность будет в точке, соответствующей сопряженной частоте, и равна около 3 дБ. На практике обычно используют асимптотические характеристики. Их основное преимущество в том, что при изменении параметров системы (k и T) характеристики перемещаются параллельно самим себе.
Примеры звена:
1. Апериодическое звено может быть реализовано на операционных усилителях (рис. 9).
Сoc
Rос Rвх Uвых K(p) = k/(Tp+1); T = RосCос; k = RосRвх.
Uвх
Рис. 9
2. Звенья на RLC-цепях (рис. 10).
L
R Uвх С Uвх
R
Uвых Uвых
Рис. 10
4. Механические демпферы (рис. 11).
Y
X
Рис. 11
Интегрирующее звено. Интегрирующим звеном называют звено, которое описывается уравнением:
(6)
или передаточной функцией:
(7)
При этом переходная функция интегрирующего звена (рис. 12а) и его функция веса (рис. 12б) соответственно имеют вид:
t
а)
h(t)
1/Т
1/T
k(t)
t
6)
Рис. 12
Частотные характеристики интегрирующего звена (рис. 13) определяются соотношениями:
0
-/2
АЧХ
A()
0
ФЧХ
()
+j
+
АФХ
=
h(t)
Рис. 13
Логарифмические частотные характеристики интегрирующего звена (рис. 14) определяются по формуле:
0
ЛАЧХ
L()
-20 дБ/дек
с
+20
-20
0.1 1 10 100
Рис. 14
Пример звена. Интегрирующее звено может быть реализовано на операционных усилителях (рис. 15).
Rвх
Uвых
Uвх
Сoc
K(p) = 1/Tp; T = RвхCос.
Рис. 15
Дифференцирующее звено. Дифференцирующим называют звено, которое описывается уравнением:
(8)
или передаточной функцией:
(9)
При этом переходная функция звена (рис. 16а) и его функция веса (рис. 16б) соответственно имеют вид:
k(t)= T(t)
0 t
б)
h(t)=T(t)
t
а)
Рис. 16
Частотные характеристики звена (рис. 17а-в) определяются соотношениями:
+
АЧХ
0
0
A()
T0
ФЧХ
0
0
()
/2
+j
АФХ
=
а) б) б)
Рис. 17
Идеальное дифференцирующее звено является физически не реализуемым. В реальных звеньях такой вид характеристики могут иметь только в ограниченном диапазоне частот.
Логарифмические частотные характеристики звена (рис. 18) определяются по формуле:
0
ЛАЧХ
L()
20 дБ/дек
с
+20
-20
0.1 1 10 100
Рис. 18
Примеры звена:
1. Дифференцирующее звено может быть реализовано на операционных усилителях (рис. 19).
Cвх
Uвых
Uвх
Roc
K(p)=Tp; T=CвхRос.
Рис. 19
2. Тахогенератор (рис. 20).
x =
y = U
Рис. 20
Колебательное звено. Колебательным называют звено, которое описывается уравнением:
(10)
или передаточной функцией:
(11)
где – демпфирование (0 1).
Если = 0, то демпфирование отсутствует (консервативное звено – без потерь), если = 1, то имеем два апериодических звена.
При этом переходная функция звена и его функция веса (рис. 21) соответственно имеют вид:
(12)
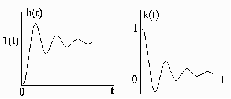 а) б)
а) б)
Рис. 21
Амплитудно-фазовая частотная характеристика (АФХ) имеет вид (рис. 22а) и определяется соотношением
Амплитудно-частотные характеристики (АЧХ) для различных значений имеет вид (рис. 22б) и определяется соотношением
Фазовая частотная характеристика (ФЧХ) имеет вид (рис. 22в) и определяется соотношением
Частотные характеристики колебательного звена имеют вид
=
K(j)
+j
k +
АФХ
ФЧХ
0
0
()
-
c=1/T
-/2
АЧХ
0
0
A()
k
а) б) в)
Рис. 22
Логарифмические частотные характеристики звена (рис. 23) определяются по формуле:
При k = 1
0
ЛАЧХ
L()
-40 дБ/дек
с
+20
-20
0.1 1 10 100
+40
-40
Рис. 23
Примеры звена. Колебательное звено может быть реализовано на операционных усилителях (рис. 24).
Сос Сос Rос
Uвх Uвых
Rвх Rвх Rвх
Рис. 24
Колебательное звено на RLC-цепи (рис. 25).
R L
Uвых Uвх
С
Рис. 25
В приведенной схеме:
С – накапливает энергию электрического поля;
L – накапливает энергию электромагнитного поля;
R – на сопротивлении происходит потеря энергии.
Запишем передаточную функцию цепи:
– затухание (демпфирование).
4. Механические демпферы (рис. 26).
Y
X
С
m
Рис. 26
Форсирующее звено. Форсирующим называют звено, которое описывается уравнением:
(13)
или передаточной функцией
(14)
где k – коэффициент передачи звена.
При этом переходная функция звена и его функция веса соответственно определяются соотношениями:
Частотные характеристики звена (рис. 27а-в) определяются соотношениями:
A()
+
АЧХ
0
0
ФЧХ
0
0
()
/2
/4
= с
+j
АФХ
1
1
а) б) в)
Рис. 27
Логарифмические частотные характеристики звена (рис. 28) определяются по формуле:
+20
0
-20
ЛАЧХ
L()
+20 дБ/дек
с
0.1 1 10 100
Рис. 28
Форсирующее звено 2-го порядка. Передаточная функция форсирующего звена 2-го порядка имеет вид:
(15)
Логарифмические частотные характеристики звена имеют вид:
Рис. 29
L()
+40 дБ/дек
с
+40
+20
0
-20
-40
0.1 1 10 100
Запаздывающее звено. Дифференциальное уравнение и передаточная функция запаздывающего звена имеют вид:
(16)
(17)
где – время запаздывания.
В соответствии с теоремой запаздывания . При этом переходная функция звена и его функция веса (рис. 30а, б) соответственно определяются соотношениями:
h(t) k(t)
Рис. 30
Частотные характеристики звена (рис. 31а-в) определяются соотношениями:
+
0
АЧХ
0
0
A()
1
АФХ
+j
+
1
K(j)
ФЧХ
0
()
а) б) в)
Рис. 31
Устойчивые и неустойчивые звенья. В устойчивых звеньях переходный процесс является сходящимся, а в неустойчивых он расходится. Устойчивые звенья называются минимально – фазовыми. Эти звенья не содержат нулей и полюсов в правой полуплоскости корней. Неустойчивые звенья называются не минимально – фазовыми. Т. е. изменению амплитуды на 20 дБ/дек соответствует изменение фазы на /2, а 40 дБ/дек – на .
Пример 1. Построить частотные характеристики для звеньев
Для заданных передаточных функций звеньев, характеристики имеют вид (рис. 32):
h(t)
1(t)
0 t
h(t)
1(t)
=0 = + t
K(j)
+j
= =0 + t
K(j)
+j
c t
L(),()
0
-/2
-
-3/2
c t
L(),()
0
-/2
-
-3/2
Рис. 32
Идеальные и реальные звенья. Идеальные звенья физически не реализуемы, реальные звенья содержат инерционности.
реальное интегрирующее звено;
реальное дифференцирующее звено;
реальное форсирующее звено.
АФХ этих звеньев имеют вид (рис. 33а-в):
K(j) + K(j) =0 = + +j +j
=0 = +
K(j)
а) б) в)
Рис. 33
+j
Рассмотрим характеристики соединений звеньев и порядок построения логарифмических частотных характеристик соединений звеньев.
1. Определяем, из каких элементарных звеньев состоит соединение.
2. Определяем сопрягающие частоты отдельных звеньев и откладываем их по оси частот в порядке возрастания.
3. Определяем наклон низкочастотной асимптоты, используя формулу [(-) 20] дБ/дек (где – количество дифференцирующих, а - интегрирующих звеньев) и проводим ее через соответствующую сопряженную частоту.
4. Последовательно сопрягая звенья, строим характеристику соединения.
Пример 2. Построить логарифмическую частотную характеристику соединения:
0,1 1 10 [1/c]
+60
+40
+20
0
-20
-40
-60
Рис. 34
-20
0
-20
L [дБ]
Решение: Определяем со-прягающие частоты отде-льных звеньев и отклады-ваем их по оси частот в по-рядке возрастания. Tинт = 0,01 с; инт = 100 с-1; Tфор = 1 с; фор = 1 с-1; Tап = 0,1 с; ап = 10 с-1; Строим характеристику (рис. 34).
Пример 3. Построить логарифмическую частотную характеристику соединения
L [дБ]
Решение: Определяем соп-рягающие частоты отдель-ных звеньев и откладываем их по оси частот в порядке возрастания. Tинт = 0,1 с; инт = 10 с-1; Tфор = 10 с; фор = 0,1 с-1; Tк = 1 с; к = 1 с-1; Tфор = 0,1 с; фор = 10 с-1; Tфор = 0,01 с; фор= 100 с-1; Строим характеристику рис. 35 -20 0 -20 0 -20 +60 +40 +20 0 -20 -40 -60
0,1 1 10 [1/c]
Рис. 35
Пример 4. Построить АФХ соединения звеньев, передаточная функция которого имеет вид
Решение: Выполнив подстановку p = j и умножив на комплексно сопряженное выражение, получим
Строим характеристику рис. 36.
АФХ
+j
K(j)
+
Рис. 36
Литература
Автоматизированное проектирование систем автоматического управления. / Под ред. В.В. Солодовникова. – М.: Машиностроение, 1990. -332 с.
Бойко Н.П., Стеклов В.К. Системы автоматического управления на базе микро-ЭВМ. – К.: Тэхника, 1989. –182 с.
В.А. Бесекерский, Е.П. Попов «Теория систем автоматического управления». Профессия, 2003 г. – 752 с.
Гринченко А.Г. Теория автоматического управления: Учебн. пособие. – Харьков: ХГПУ, 2000. –272 с.
Справочник по теории автоматического управления. /Под ред. А.А. Красовского – М.: Наука, 1987. – 712 с.

Нравится материал? Поддержи автора!
Ещё документы из категории коммуникации, связь:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ