Вариация, дисперсионный анализ статистических данных



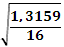
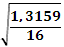
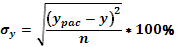
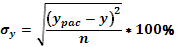
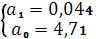
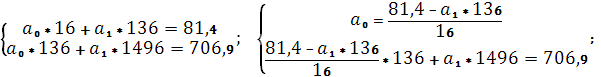
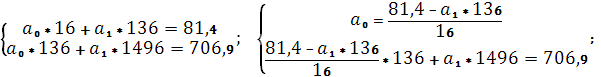
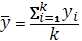
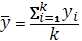
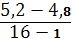
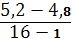
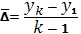
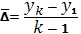
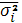
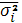
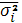
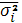
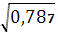
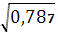
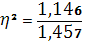
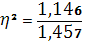
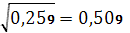
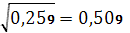
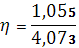
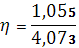
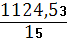
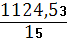
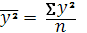
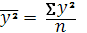
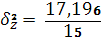
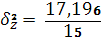
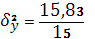
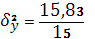
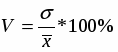
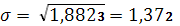
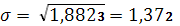
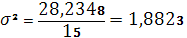
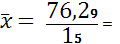
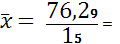
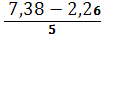
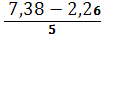
Федеральное агентство по образованию
Государственное образовательное учреждение
Высшего профессионального образования
«Тульский государственный университет»
Кафедра «Экономики и управление»
СТАТИСТИКА
КОНТРОЛЬНО-КУРСОВАЯ РАБОТА
Шифр 2457
Тула 2010г.
Задание 1.
Тема: «Вариация, дисперсионный анализ статистических данных»
Имеются 15 статистических наблюдений по трем показателям предприятий. Требуется построить интервальный вариационный ряд по номеру показателя, соответствующему первой цифре шифра варианта, и используя правило сложения дисперсий, рассчитать влияние на колеблемость группировочного признака основных и второстепенных факторов.
№
наблюдения
№ показателя
1
2
3
Стоимость основных производственных фондов
Объем реализованной продукции
Объем прибыли
1
10,5
5,65
2,12
2
12,3
2,32
1,45
3
8,4
4,68
3,23
4
10,7
5,57
2,42
5
4,2
7,26
4,35
6
7,5
3,34
2,26
7
9,6
5,48
3,28
8
8,2
2,26
1,14
9
10,7
6,49
4,32
10
7,6
7,38
5,24
11
6,5
5,48
4,25
12
8,1
4,34
2,16
13
5,9
3,29
1,14
14
8,3
6,17
3,23
15
7,8
3,52
2,42
(Млн.руб)
Решение:
Построим интервальный вариационный ряд:
Количество интервалов определим с помощью формулы Стерджесса:
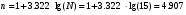 ,
,
где N – объем совокупности (количество исходных значений).
В нашем случае N=15.
Количество интервалов обязательно должно быть целым числом. Примем n=5.
Вычислим размах вариации R = xmax – xmin.
Величина равного интервала (шаг варьирования) рассчитывается по формуле:
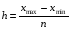
где n = 5 – число групп
хmin и хmax – максимальное и минимальное значения признака.
Найдем наименьшее и наибольшее значения
хmin = 2,26 хmax = 7,38
Получаем величину интервала:
h = =1,02
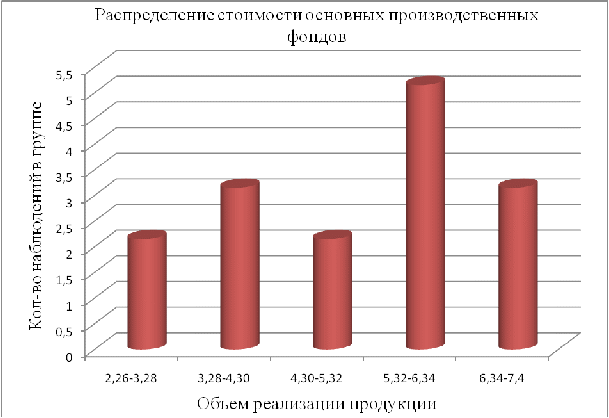
Составим таблицу по сгруппированным данным, используя принцип единообразия (левое число включает в себя обозначающее значение, а правое нет, в данном случае с избытком будет последний интервал):
№
группы
Интервал
№ наблюдения
Кол-во
Объем реализованной продукции
1
2,26-3,28
2
2
2,32
4,58
8
2,26
2
3,28-4,30
6
3
3,34
10,15
13
3,29
15
3,52
3
4,30-5,32
3
2
4,68
9,02
12
4,34
4
5,32-6,34
1
5
5,65
28,35
4
5,57
7
5,48
11
5,48
14
6,17
5
Свыше 6,34
5
9
10
3
7,26
6,49
7,38
21,13
Итог
15
73,23
Итоговая таблица:
Интервал
Середина интервала
Частота
2,26-3,28
2,77
2
3,28-4,30
3,79
3
4,30-5,32
4,81
2
5,32-6,34
5,83
5
6,34-7,4
6,87
3
Итого
15
Определение характеристик ряда распределения
Среднее квадратическое отклонение - это обобщающая характеристика абсолютных размеров вариации признака в совокупности.
Для вычисления среднего квадратического отклонения необходимо вычислить дисперсию. Необходимо воспользоваться следующей формулой для расчета взвешенной дисперсии:
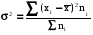 .
.
Среднее квадратическое отклонение представляет собой корень квадратный из дисперсии:
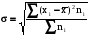 – среднее квадратическое отклонение взвешенное.
– среднее квадратическое отклонение взвешенное.
Определение характеристик ряда распределения
Группы по стоимости основных производственных фондов, млн. руб.
Число наблюдений fi
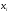
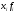
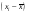
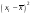
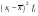
2,26-3,28
2
2,77
5,54
-2,32
5,3824
10,7648
3,28-4,30
3
3,79
11,37
-1,3
1,69
5,07
4,30-5,32
2
4,81
9,62
0,28
0,0784
0,1568
5,32-6,34
5
5,83
29,15
0,74
0,5476
2,738
6,34-7,4
3
6,87
20,61
1,78
3,1684
9,5052
Итого
15
-
76,29
-
-
28,2348
Средняя арифметическая ряда распределения рассчитывается следующим образом:
Получаем:
5,09 млн. руб.
Вычислим общую дисперсию и среднеквадратическое отклонение:
млн. руб.
Среднеквадратическое отклонение показывает, что значение признака в совокупности отклоняется от средней величины в ту или иную сторону в среднем на 1,372 млн. руб.
Рассчитаем коэффициент вариации:
V = 1,372/5,09*100=27%
Значение коэффициента вариации менее 33%. Следовательно, можно сделать вывод, что рассматриваемая совокупность является не однородной.
Составим рабочую аналитическую таблицу:
Интервал
№ наблюдения
Объем реализованной продукции
Стоимость основных производственных фондов
Объем
прибыли
2,26-3,28
2
2,32
12,3
1,45
8
2,26
8,2
1,14
Итого
-
4,58
20,5
2,59
В среднем
-
2,29
10,25
1,295
3,28-4,30
6
3,34
7,5
2,26
13
3,29
5,9
1,14
15
3,52
7,8
2,42
Итого
-
10,15
21,2
5,82
В среднем
-
3,38
7,07
1,94
4,30-5,32
3
4,68
8,4
3,23
12
4,34
8,1
2,16
Итого
-
9,02
16,5
5,39
В среднем
-
4,51
8,25
2,695
5,32-6,34
1
5,65
10,5
2,12
4
5,57
10,7
2,42
7
5,48
9,6
3,28
11
5,48
6,5
4,25
14
6,17
8,3
3,23
Итого
-
28,35
45,6
15,3
В среднем
-
5,67
9,12
3,06
6,34-7,4
5
7,26
4,2
4,35
9
6,49
10,7
4,32
10
7,38
7,6
5,24
Итого
-
21,13
22,5
13,91
В среднем
-
7,04
7,5
4,64
Всего
15
73,23
126,3
43,01
В среднем
-
4,882
8,42
2,87
Итоговая аналитическая таблица будет иметь вид:
Интервал
Количество наблюдений в группе
Стоимость основных производственных фондов
Объем реализованной продукции
Объем
прибыли
Всего
В среднем
Всего
В среднем
Всего
В среднем
2,26-3,28
2
20,5
10,25
4,58
2,29
2,59
1,295
3,28-4,30
3
21,2
7,07
10,15
3,38
5,82
1,94
4,30-5,32
2
16,5
8,25
9,02
4,51
5,39
2,695
5,32-6,34
5
45,6
9,12
28,35
5,67
15,3
3,06
6,34-7,4
3
22,5
7,5
21,13
7,04
13,91
4,64
Итого
15
126,3
8,42
73,23
4,882
43,01
2,87
Для определения тесноты и характера связи между изучаемыми признаками проведем дополнительные расчеты
Расчет межгрупповой дисперсии
Группы по стоимости основных производственных фондов, млн. руб.
Число
наблюдений ni
Стоимость основных производственных фондов, млн.руб.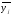
(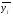 -
- )2 *ni
)2 *ni
Объем
прибыли,
млн. руб. 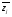
(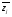 -
-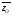 )2 *ni
)2 *ni
2,26-3,28
2
10,25
6,698
1,295
4,961
3,28-4,30
3
7,07
5,468
1,94
2,595
4,30-5,32
2
9,12
0,98
2,695
0,06
5,32-6,34
5
8,25
0,145
3,06
0,181
6,34-7,4
3
7,5
2,539
4,64
9,399
Итого
15
-
15,83
-
17,196
 = 8,42 млн. руб.
= 8,42 млн. руб. 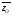 = 2,87 млн. руб.
= 2,87 млн. руб.
Рассчитаем межгрупповую дисперсию признака по формуле:
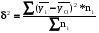
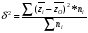
Получим значение межгрупповой дисперсии признака:
=1,055 = 1,146
Межгрупповая дисперсия характеризует вариацию групповых средних, обусловленных стоимости ОПФ и объемом реализации продукции.
Рассчитаем среднее значение квадрата признака
№ п/п
Стоимость основных производственных фондов, млн. руб. 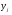
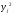
Объем прибыли, млн. руб. 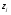
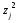
1
10,5
110,25
2,12
4,4944
2
12,3
151,29
1,45
2,1025
3
8,4
70,56
3,23
10,4329
4
10,7
114,49
2,42
5,8564
5
4,2
17,64
4,35
18,9225
6
7,5
56,25
2,26
5,1076
7
9,6
92,16
3,28
10,7584
8
8,2
67,24
1,14
1,2996
9
10,7
114,49
4,32
18,6624
10
7,6
57,76
5,24
27,4576
11
6,5
42,25
4,25
18,0625
12
8,1
65,61
2,16
4,6656
13
5,9
34,81
1,14
1,2996
14
8,3
68,89
3,23
10,4329
15
7,8
60,84
2,42
5,8564
Итого
126,3
1124,53
43,01
145,4113
Среднее значение квадрата признака 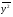 :
:
= = 74,969млн. руб.
Квадрат среднего значения признака:
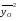 = 8,422 = 70,8964
= 8,422 = 70,8964
Величина общей дисперсии будет равна:
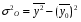
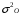 = 74,969-70,8964 =4,073
= 74,969-70,8964 =4,073
Коэффициент детерминации представляет собой долю межгрупповой дисперсии в общей дисперсии и характеризует силу влияния группировочного признака на образование общей вариации:
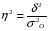 = 0,259
= 0,259
Т.е. на 25,9% вариация объема реализованной продукции обусловлена различиями стоимости ОПФ.
Эмпирическое корреляционное отношение:
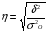 �� =
�� =
Можно сказать, что взаимосвязь между рассматриваемыми признаками: объем реализованной продукции и стоимость основных производственных фондов 50,9%.
Среднее значение квадрата признака 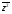 :
:
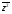 = = 9,694млн. руб.
= = 9,694млн. руб.
Квадрат среднего значения признака:
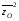 = 2,872 = 8,237
= 2,872 = 8,237
Величина общей дисперсии будет равна:
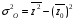
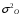 = 9,694-8,237=1,457
= 9,694-8,237=1,457
Коэффициент детерминации представляет собой долю межгрупповой дисперсии в общей дисперсии и характеризует силу влияния группировочного признака на образование общей вариации:
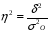 = 0,787
= 0,787
Т.е. на 78,7% вариация объема реализованной продукции обусловлена различиями объема прибыли.
Эмпирическое корреляционное отношение:
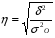 �� = = 0,887
�� = = 0,887
Можно сказать, что взаимосвязь между рассматриваемыми признаками стоимость основных производственных фондов и объем реализованной продукции сильная на 88,7%.
Используя правило сложения дисперсий, вычислим среднюю из внутригрупповых дисперсий, которая отражает влияние неучтенных факторов. Согласно данному правилу, общая дисперсия равна сумме средней из внутригрупповых и межгрупповой дисперсии:
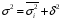
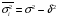
Средняя из внутригрупповых дисперсий равна для признака Y:
=4,073-1,055=3,018
Средняя из внутригрупповых дисперсий равна для признака Z:
=1,457-1,146=0,311
Задание 2.
Тема: «Ряды динамики»
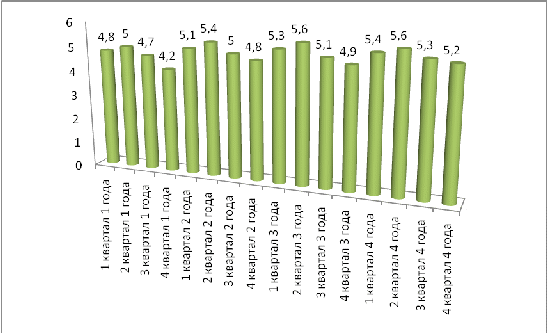
Построить ряд динамики, включающий четыре года соответствующих шифру варианта. Рассчитать показатели уровня ряда динамики. Построить уравнение тренда. Оценить сезонные колебания. Сделать прогноз по показателю уровня ряда динамики (по объему реализованной продукции на пятый год в разрезе четырех кварталов). Рассчитать среднюю ошибку прогнозирования.
Квартал
Объемы реализованной продукции по годам млн.руб
1
2
3
4
5
6
7
8
1-ый
4,6
4,8
5,0
5,1
5,3
5,2
5,4
5,5
2-ой
5,2
5,0
5,1
5,4
5,6
5,4
5,6
5,8
3-ий
4,8
4,7
4,9
5,0
5,1
5,2
5,3
5,6
4-ый
4,4
4,2
4,5
4,8
4,9
5,0
5,2
5,3
Решение:
1) Рассчитаем абсолютные приросты
Год/квартал
цепные 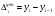
базисные 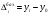
2
1-ый
-
-
2-ой
5,0-4,8 = 0,2
5,0-4,8=0,2
3-ий
4,7-5,0 =-0,3
4,7-4,8=-0,1
4-ый
4,2-4,7=-0,5
4,2-4,8=-0,6
3
1-ый
5,1-4,2=0,9
5,1-4,8=0,3
2-ой
5,4-5,1=0,3
5,4-4,8=0,6
3-ий
5,0-5,4=-0,4
5,0-4,8=0,2
4-ый
4,8-5,0=-0,2
4,8-4,8=0
4
1-ый
5,3-4,8=0,5
5,3-4,8=0,5
2-ой
5,6-5,3=0,3
5,6-4,8=0,8
3-ий
5,1-5,6=-0,5
5,1-4,8=0,3
4-ый
4,9-5,1=-0,2
4,9-4,8=0,1
8
1-ый
5,4-4,9=0,5
5,4-4,8=0,6
2-ой
5,6-5,4=0,2
5,6-4,8=0,8
3-ий
5,3-5,6=-0,3
5,3-4,8=0,5
4-ый
5,2-5,3=-0,2
5,2-4,8=0,4
Рассчитаем темпы роста и прироста
Год
базисные 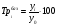
базисные 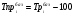
цепные 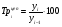
цепные 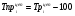
2
1-ый
4,8
-
-
-
-
2-ой
5,0
104,17
4,17
104,17
4,17
3-ий
4,7
97,92
-2,08
94,00
-6,00
4-ый
4,2
87,50
-12,50
89,36
-10,64
3
1-ый
5,1
106,25
6,25
121,43
21,43
2-ой
5,4
112,50
12,50
105,88
5,88
3-ий
5
104,17
4,17
92,59
-7,41
4-ый
4,8
100,00
0,00
96,00
-4,00
4
1-ый
5,3
110,42
10,42
110,42
10,42
2-ой
5,6
116,67
16,67
105,66
5,66
3-ий
5,1
106,25
6,25
91,07
-8,93
4-ый
4,9
102,08
2,08
96,08
-3,92
5
1-ый
5,4
112,50
12,50
110,20
10,20
2-ой
5,6
116,67
16,67
103,70
3,70
3-ий
5,3
110,42
10,42
94,64
-5,36
4-ый
5,2
108,33
8,33
98,11
-1,89
Абсолютное содержание одного процента прироста 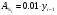
Год
Год
(Продолжение)
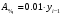
1-ый
4,8
-
1-ый
5,3
0,048
2-ой
5
0,048
2-ой
5,6
0,053
3-ий
4,7
0,05
3-ий
5,1
0,056
4-ый
4,2
0,047
4-ый
4,9
0,051
1-ый
5,1
0,042
1-ый
5,4
0,049
2-ой
5,4
0,051
2-ой
5,6
0,054
3-ий
5
0,054
3-ий
5,3
0,056
4-ый
4,8
0,05
4-ый
5,2
0,053
Средний абсолютный прирост = =0,027 млн. руб.
Средний уровень интервального ряда динамики, состоящего из абсолютных величин, определяется по формуле средней арифметической
= =5,0875 млн. руб.
Покажем ряд динамики:
Построим уравнение тренда в виде:
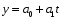
Где 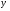 - выровненный показатель объема реализованной продукции
- выровненный показатель объема реализованной продукции
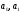 - параметры линейного тренда
- параметры линейного тренда
 - порядковый номер соответствующего квартала соответствующего года.
- порядковый номер соответствующего квартала соответствующего года.
Параметры линейного тренда определяем методом наименьших квадратов, решив следующую систему уравнений с двумя неизвестными:
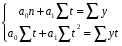
Рассчитаем необходимые параметры в таблице:
Квартал
t
y
y*t
t2
1-ый
1
4,8
4,8
1
2-ой
2
5
10
4
3-ий
3
4,7
14,1
9
4-ый
4
4,2
16,8
16
1-ый
5
5,1
25,5
25
2-ой
6
5,4
32,4
36
3-ий
7
5
35
49
4-ый
8
4,8
38,4
64
1-ый
9
5,3
47,7
81
2-ой
10
5,6
56
100
3-ий
11
5,1
56,1
121
4-ый
12
4,9
58,8
144
1-ый
13
5,4
70,2
169
2-ой
14
5,6
78,4
196
3-ий
15
5,3
79,5
225
4-ый
16
5,2
83,2
256
Итого:
136
81,4
706,9
1496
Подставляем рассчитанные значения в систему и решаем ее:
→
Модель линейного тренда имеет вид:
y=4,71+0,044t
Рассчитаем среднюю ошибку аппроксимации:
Квартал
t
y
yрасч
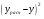
1-ый
1
4,8
4,754
0,00212
2-ой
2
5
4,798
0,04080
3-ий
3
4,7
4,842
0,02016
4-ый
4
4,2
4,886
0,47060
1-ый
5
5,1
4,93
0,02890
2-ой
6
5,4
4,974
0,18148
3-ий
7
5
5,018
0,00032
4-ый
8
4,8
5,062
0,06864
1-ый
9
5,3
5,106
0,03764
2-ой
10
5,6
5,15
0,20250
3-ий
11
5,1
5,194
0,00884
4-ый
12
4,9
5,238
0,11424
1-ый
13
5,4
5,282
0,01392
2-ой
14
5,6
5,326
0,07508
3-ий
15
5,3
5,37
0,00490
4-ый
16
5,2
5,414
0,04580
Итого:
136
81,4
81,344
1,3159
Средняя ошибка аппроксимации составляет
= *100% = 28,68%
Сделать прогноз по показателю уровня ряда динамики (по объему реализованной продукции на пятый год в разрезе четырех кварталов):
-
5-й год
t
yрасч
1-ый
17
5,458
2-ой
18
5,502
3-ий
19
5,546
4-ый
20
5,590
Рассчитаем индексы сезонности, для этого необходимо дополнительно рассчитать среднюю величину объема реализованной продукции по каждому кварталу за четыре года. Все расчеты произведем в таблице:
квартал
Объем реализованной продукции, млн. руб.
В среднем за четыре года
Индекс сезонности 
2
4
5
7
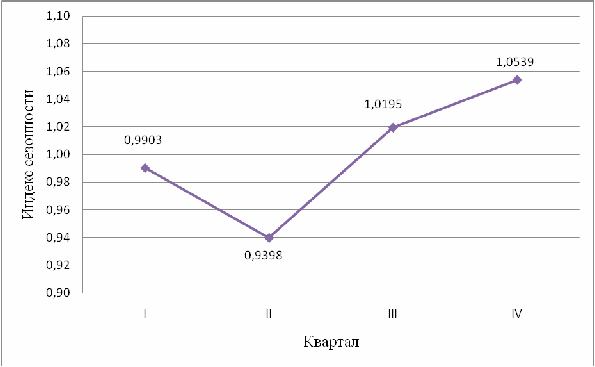
I
4,8
5
5,1
5,5
5,1
0,9903
II
5,1
5,4
5
4,8
5,075
0,9398
III
5,3
5,6
5,1
4,9
5,225
1,0195
IV
5,4
5,6
5,3
5,2
5,375
1,0539
итого
20,6
21,6
20,5
20,4
20,175
4,0035
среднее
5,15
5,4
5,125
5,1
5,1938
1,0009
Построим график сезонной волны:
Задание 3. Тема: «Корреляционно-регрессионный анализ»
По результатам 10 наблюдений построить с использованием стандартной программы расчета на ЭВМ четырехфакторную линейную регрессионную модель показателя У. Номера факторов соответствуют шифру варианта. Сделать прогноз значения показателя У от заданных значений факторов. Рассчитать среднюю ошибку аппроксимации прогноза.
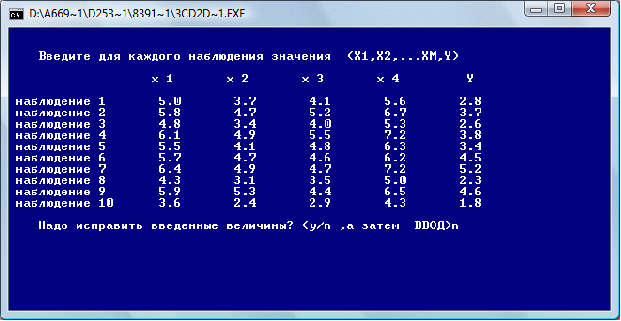
Результаты статистических наблюдений
№
Наблю-
дения
Y
ФАКТОРЫ
X1
X2
X3
X4
X5
X6
X7
X8
Х9
1
2,8
3,4
5,0
2,5
3,7
4,1
4,5
5,6
3,1
4,2
2
3,7
4,4
5,8
3,6
4,7
5,2
5,5
6,7
4,3
5,3
3
2,6
3,6
4,8
2,4
3,4
4,0
4,2
5,3
2,8
4,0
4
3,8
4,5
6,1
3,7
4,9
5,5
6,0
7,2
4,7
5,6
5
3,4
4,2
5,5
3,2
4,1
4,8
5,2
6,3
3,7
4,9
6
4,5
5,4
5,7
2,9
4,7
4,6
5,3
6,2
3,4
5,1
7
5,2
6,0
6,4
4,2
4,9
4,7
6,3
7,2
4,5
6,7
8
2,3
3,2
4,3
1,9
3,1
3,5
3,9
5,0
2,3
2,8
9
4,6
5,1
5,9
3,2
5,3
4,4
5,7
6,5
3,8
5,9
10
1,8
2,5
3,6
1,3
2,4
2,9
3,2
4,3
1,5
3,5
Прогнозные
значения
факторов Xi
6,5
7,3
5,6
6,2
5,0
8,2
7,9
5,6
6,5
Решение:
Введем исходные данные задачи:
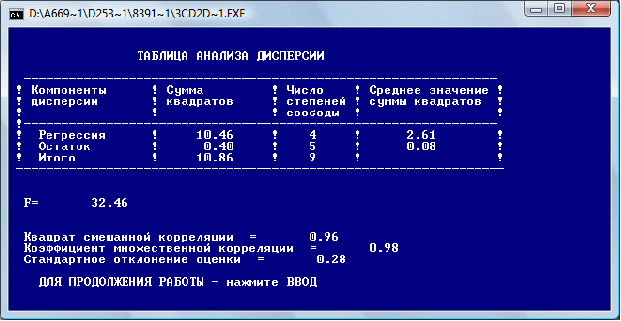
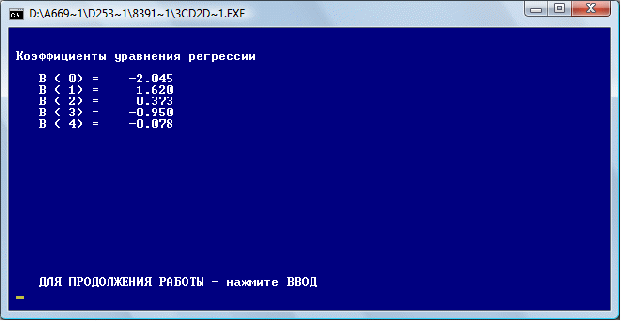
После нажатия «Ввод» получаем коэффициенты четырехфакторной регрессии:
Тогда уравнение четырехфакторной регрессии будет иметь вид:
Y = -2,045+1,62х1+0,373х2+-0,95х3-0,078х4
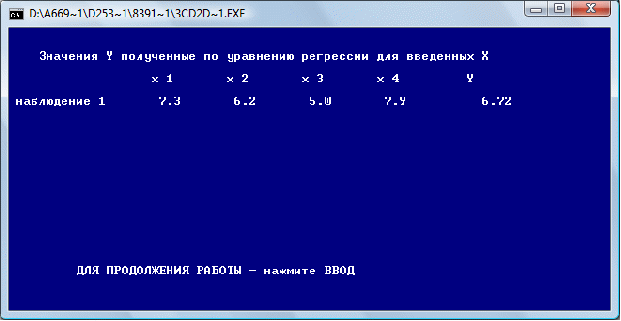
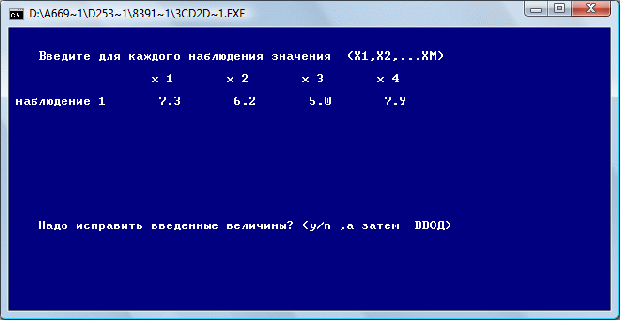
Сделаем прогноз значения показателя У от заданных значений факторов.
Введем прогнозное значение факторов Хi:
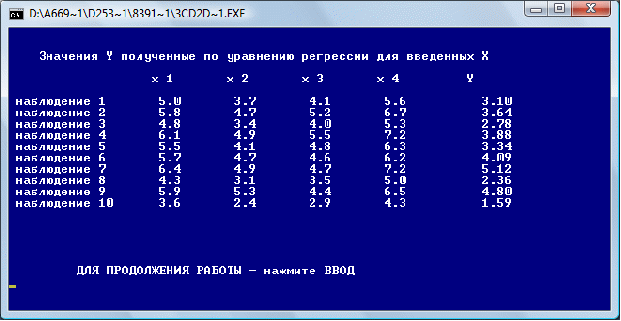
Получим значение Y по уравнению регрессии:
Рассчитаем среднюю ошибку аппроксимации прогноза:
№ Наблюдения
Y
yрасч
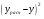
1
2,8
3,10
0,0900
2
3,7
3,64
0,0036
3
2,6
2,78
0,0324
4
3,8
3,88
0,0064
5
3,4
3,34
0,0036
6
4,5
4,09
0,1681
7
5,2
5,12
0,0064
8
2,3
2,36
0,0036
9
4,6
4,80
0,0400
10
1,8
1,59
0,0441
итого
0,3982
Средняя ошибка аппроксимации составляет:

Нравится материал? Поддержи автора!
Ещё документы из категории маркетинг :
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ