Национальный Горный Университет Украины

Контрольная работа

по дисциплине

«Использование вычислительной техники»

Днепропетровск

Используя приложение Excel пакета Microsoft Office (версии 95,97, 2000 или XP) рассчитать значения функций и построить графики.

Оформить работу в текстовом редакторе Microsoft Word (все выражения должны быть набраны в редакторе формул Microsoft Equation).

Задание 1. Исследовать методами математического анализа поведение функций при заданных значениях аргумента

Алгебраические рациональные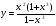

1. Область существования: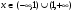

2. Четность: функция ни четная, ни нечетная

3. Точки разрыва: . Промежутки непрерывности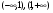

4. Точки пересечения функции с осями координат: (-1,0), (0,0).

5. Экстремум функции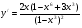

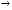
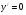
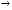
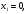
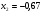
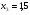
x

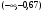
-0,67

(-0,67; 0)

0

(0,1)

(1;1,5)

1,5

(1,5;+)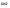

y^/

+

0

–

0

+

+

0

–

y

возрастает

0,23

убывает

0

возрастает

возрастает

-4,14

убывает

6. Вертикальная асимптота

Значения функции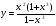

x

y

x

y

-3

-8,35714

0,1

0,01002

-2,9

-7,74751

0,2

0,040645

-2,8

-7,15684

0,3

0,094995

-2,7

-6,58507

0,4

0,18188

-2,6

-6,03218

0,5

0,321429

-2,5

-5,49812

0,6

0,558367

-2,4

-4,98288

0,7

1,001629

-2,3

-4,48648

0,8

1,982951

-2,2

-4,00896

0,9

5,16786

-2,1

-3,55043

1

-2

-3,11111

1,1

-8,52118

-1,9

-2,69131

1,2

-5,39604

-1,8

-2,29152

1,3

-4,51373

-1,7

-1,91249

1,4

-4,20771

-1,6

-1,55529

1,5

-4,14474

-1,5

-1,22143

1,6

-4,21375

-1,4

-0,91299

1,7

-4,36713

-1,3

-0,63276

1,8

-4,58106

-1,2

-0,38428

1,9

-4,84229

-1,1

-0,17182

2

-5,14286

-1

0

2,1

-5,47767

-0,9

0,126958

2,2

-5,84332

-0,8

0,206561

2,3

-6,23743

-0,7

0,23971

2,4

-6,65832

-0,6

0,232105

2,5

-7,1047

-0,5

0,194444

2,6

-7,57564

-0,4

0,140752

2,7

-8,07039

-0,3

0,085268

2,8

-8,58838

-0,2

0,039365

2,9

-9,12914

-0,1

0,00998

3

-9,69231

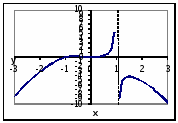
График функции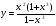

Алгебраические иррациональные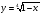

1. Область существования: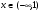

2. Четность: 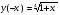функция ни четная, ни нечетная

3. Функция непрерывна

4. Точки пересечения функции с осями координат: (0, 1), (1,0).

5. Экстремум функции 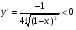, следовательно, функция y(x) убывает

6. Выпуклость, вогнутость функции:

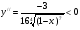, следовательно, кривая выпукла

Значения функции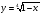

x

y

x

y

-3

1,414214

-1

1,189207

-2,9

1,405291

-0,9

1,174055

-2,8

1,396194

-0,8

1,158292

-2,7

1,386917

-0,7

1,141858

-2,6

1,377449

-0,6

1,124683

-2,5

1,367782

-0,5

1,106682

-2,4

1,357906

-0,4

1,087757

-2,3

1,347809

-0,3

1,06779

-2,2

1,337481

-0,2

1,046635

-2,1

1,326907

-0,1

1,024114

-2

1,316074

0

1

-1,9

1,304967

0,1

0,974004

-1,8

1,293569

0,2

0,945742

-1,7

1,281861

0,3

0,914691

-1,6

1,269823

0,4

0,880112

-1,5

1,257433

0,5

0,840896

-1,4

1,244666

0,6

0,795271

-1,3

1,231493

0,7

0,740083

-1,2

1,217883

0,8

0,66874

-1,1

1,203801

0,9

0,562341

-1

1,189207

1

0

График функции

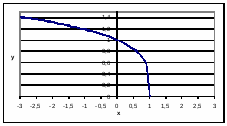
Тригонометрические: функция

1. Область существования: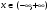

2. Четность: 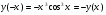функция нечетная

3. Функция непрерывна

4. Точки пересечения функции с осями координат: (0, 0), (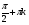,0),

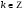
5. Экстремум функции ,

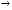
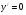
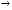
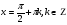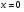
Значения функции

x

y

x

y

x

y

x

y

-31,4

-30947,4

-17,27

0

3,14

-30,959

17,27

-0,00346

-30,615

-9676,29

-16,485

1623,773

3,925

-21,5061

18,055

2023,979

-29,83

0,091927

-15,7

3869,525

4,71

0

18,84

6686,259

-29,045

9048,639

-14,915

1146,551

5,495

58,17235

19,625

2752,484

-28,26

22562,26

-14,13

0

6,28

247,6694

20,41

0,009432

-27,475

7028,394

-13,345

-857,374

7,065

126,0212

21,195

-3258,35

-26,69

0

-12,56

-1981,26

7,85

0

21,98

-10617

-25,905

-6390,02

-11,775

-566,904

8,635

-224,652

22,765

-4316,48

-25,12

-15847,2

-10,99

0

9,42

-835,868

23,55

-0,02226

-24,335

-4907,58

-10,205

381,5954

10,205

-381,595

24,335

4907,579

-23,55

0

-9,42

835,8683

10,99

-0,00023

25,12

15847,22

-22,765

4316,479

-8,635

224,6522

11,775

566,9042

25,905

6390,015

-21,98

10617,01

-7,85

0

12,56

1981,265

26,69

0,047166

-21,195

3258,345

-7,065

-126,021

13,345

857,3739

27,475

-7028,39

-20,41

0

0

0

14,13

0,001039

28,26

-22562,3

-19,625

-2752,48

0,785

0,171231

14,915

-1146,55

29,045

-9048,64

-18,84

-6686,26

1,57

0

15,7

-3869,52

29,83

-0,09193

-18,055

-2023,98

2,355

-4,60118

16,485

-1623,77

30,615

9676,285

31,4

30947,37

График функции

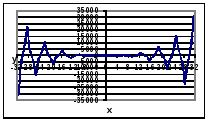
Гиперболические: функция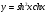

1. Область существования: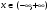

2. Четность: 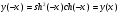функция четная

3. Функция непрерывна

4. Точки пересечения функции с осями координат: (0, 0)

5. Экстремум функции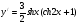

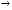
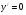
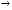
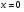
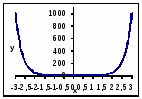
Значения функции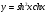

x

y

x

y

x

y

-3

1010,369

-1

2,131145

1

2,131145

-2,9

748,0854

-0,9

1,510096

1,1

2,976561

-2,8

553,8202

-0,8

1,054878

1,2

4,125531

-2,7

409,9402

-0,7

0,722286

1,3

5,685108

-2,6

303,383

-0,6

0,480502

1,4

7,799941

-2,5

224,4723

-0,5

0,306196

1,5

10,66543

-2,4

166,0397

-0,4

0,182396

1,6

14,54546

-2,3

122,7752

-0,3

0,096937

1,7

19,79642

-2,2

90,74509

-0,2

0,04135

1,8

26,8995

-2,1

67,03564

-0,1

0,010084

1,9

36,50441

-2

49,48836

0

0

2

49,48836

-1,9

36,50441

0,1

0,010084

2,1

67,03564

-1,8

26,8995

0,2

0,04135

2,2

90,74509

-1,7

19,79642

0,3

0,096937

2,3

122,7752

-1,6

14,54546

0,4

0,182396

2,4

166,0397

-1,5

10,66543

0,5

0,306196

2,5

224,4723

-1,4

7,799941

0,6

0,480502

2,6

303,383

-1,3

5,685108

0,7

0,722286

2,7

409,9402

-1,2

4,125531

0,8

1,054878

2,8

553,8202

-1,1

2,976561

0,9

1,510096

2,9

748,0854

-1

2,131145

1

2,131145

3

1010,369

График функции

Натуральные логарифмы: функция

1. Область существования: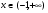

2. Четность: 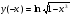функция ни четная, ни нечетная

3. Функция непрерывна. 4. Точки пересечения функции с осями координат: (0, 0)

5. Экстремум функции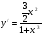

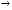
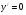
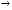
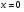
6. Точки перегиба: ,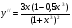

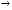
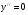
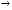
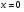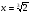
Значения функции

x

y

x

y

-1

1

0,346574

-0,9

-0,65282

1,1

0,423149

-0,8

-0,35872

1,2

0,501784

-0,7

-0,21004

1,3

0,581106

-0,6

-0,12167

1,4

0,660077

-0,5

-0,06677

1,5

0,737953

-0,4

-0,03307

1,6

0,814228

-0,3

-0,01369

1,7

0,888577

-0,2

-0,00402

1,8

0,960809

-0,1

-0,0005

1,9

1,03083

0

0

2

1,098612

0,1

0,0005

2,1

1,164175

0,2

0,003984

2,2

1,227567

0,3

0,013321

2,3

1,288857

0,4

0,031018

2,4

1,348124

0,5

0,058892

2,5

1,405454

0,6

0,097783

2,6

1,460935

0,7

0,147453

2,7

1,514656

0,8

0,206717

2,8

1,566703

0,9

0,273772

2,9

1,617158

1

0,346574

3

1,666102

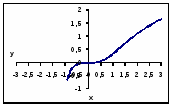
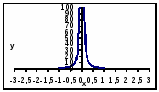
Сочетание тригонометрических, гиперболических: функция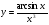

1. Область существования: 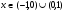. Точка разрыва .

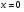2. Четность: 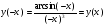функция четная.

4. Точек пересечения функции с осями координат нет.

5. Экстремум функции

Значения функции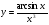

x

y

-1

1,570796

-0,9

1,536035

-0,8

1,811123

-0,7

2,260634

-0,6

2,979172

-0,5

4,18879

-0,4

6,429951

-0,3

11,28491

-0,2

25,16974

-0,1

100,1674

0

0,1

100,1674

0,2

25,16974

0,3

11,28491

0,4

6,429951

0,5

4,18879

0,6

2,979172

0,7

2,260634

0,8

1,811123

0,9

1,536035

1

1,570796

Задание 2. Выполнить исследование методами математического анализа уравнения функции и определить значения аргумента и параметра (если он имеется). Вид уравнения выбирается самостоятельно

Циссоида (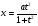

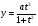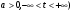
Обе функци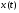и и 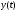определены при всех значениях . Заметим, что 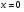, 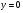при 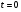. Найдем производные и :

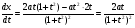
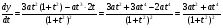
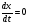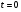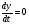при , при .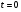

Для параметра t получили критическую точку .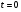

Далее, находим

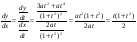
Составляем таблицу:

Область изменения t

Соответствующая область изменения x

Соответствующая область изменения y

Знак

dy/dx

Характер изменения yкак функции от x

–

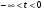
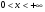
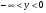
убывает

+

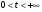
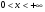
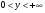
возрастает

Найдем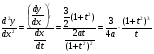

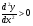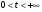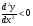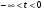при - кривая вогнута; при - кривая выпукла

Точка 0 – точка возврата (такая точка, где направление движения вдоль кривой скачкообразно меняется на противоположное).

Вертикальная асимптота: .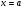

Значения функци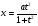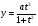и (при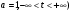

t

x

y

-3

0,9

-2,7

-2,9

0,89373

-2,59182

-2,8

0,886878

-2,48326

-2,7

0,879373

-2,37431

-2,6

0,871134

-2,26495

-2,5

0,862069

-2,15517

-2,4

0,852071

-2,04497

-2,3

0,841017

-1,93434

-2,2

0,828767

-1,82329

-2,1

0,815157

-1,71183

-2

0,8

-1,6

-1,9

0,78308

-1,48785

-1,8

0,764151

-1,37547

-1,7

0,742931

-1,26298

-1,6

0,719101

-1,15056

-1,5

0,692308

-1,03846

-1,4

0,662162

-0,92703

-1,3

0,628253

-0,81673

-1,2

0,590164

-0,7082

-1,1

0,547511

-0,60226

-1

0,5

-0,5

-0,9

0,447514

-0,40276

-0,8

0,390244

-0,3122

-0,7

0,328859

-0,2302

-0,6

0,264706

-0,15882

-0,5

0,2

-0,1

-0,4

0,137931

-0,05517

-0,3

0,082569

-0,02477

-0,2

0,038462

-0,00769

-0,1

0,009901

-0,00099

0

0

0

0,1

0,009901

0,00099

0,2

0,038462

0,007692

0,3

0,082569

0,024771

0,4

0,137931

0,055172

0,5

0,2

0,1

0,6

0,264706

0,158824

0,7

0,328859

0,230201

0,8

0,390244

0,312195

0,9

0,447514

0,402762

1

0,5

0,5

1,1

0,547511

0,602262

1,2

0,590164

0,708197

1,3

0,628253

0,816729

1,4

0,662162

0,927027

1,5

0,692308

1,038462

1,6

0,719101

1,150562

1,7

0,742931

1,262982

1,8

0,764151

1,375472

1,9

0,78308

1,487852

2

0,8

1,6

2,1

0,815157

1,71183

2,2

0,828767

1,823288

2,3

0,841017

1,93434

2,4

0,852071

2,04497

2,5

0,862069

2,155172

2,6

0,871134

2,264948

2,7

0,879373

2,374306

2,8

0,886878

2,483258

2,9

0,89373

2,591817

3

0,9

2,7

График функции

Список использованной литературы

1. Гай Харт-Девис WORD 2000. Базовый курс: Пер. с англ. – К.:ВЕК+,М:ЭНТРОП, СПБ: Корона-Принт, 2000. – 400 с., ил.

2. Джен Вейсскопф EXCEL 2000. Базовый курс (русифицированная версия): пер. с англ. – К.:ВЕК+, М.:ЭНТРОП, СПБ.: Корона-Принт, 2000. – 400 с., ил.

3. Пискунов Н.С. Дифференциальное и интегральное исчисления , том 1: учебное пособие для втузов. – 13-е изд. – М.: Наука, 1985. – 432 с.

4. Выгодский М.Я. Справочник по высшей математике. – М.:Физматгиз, 1963– 872с.