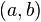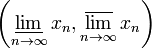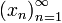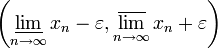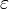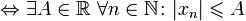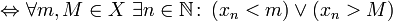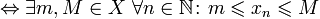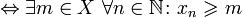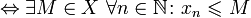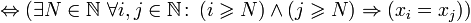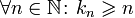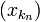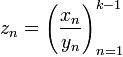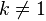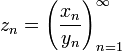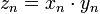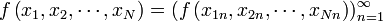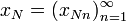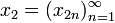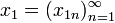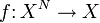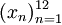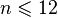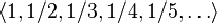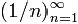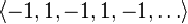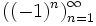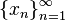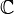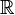Содержание

• 1 Определение

• 2 Примеры

• 3 Операции над последовательностями

• 4 Подпоследовательности

  • 4.1 Примеры

  • 4.2 Свойства

• 5 Предельная точка последовательности

• 6 Предел последовательности

• 7 Некоторые виды последовательностей

  • 7.1 Ограниченные и неограниченные последовательности

    • 7.1.1 Критерий ограниченности числовой последовательности

    • 7.1.2 Свойства ограниченных последовательностей

  • 7.2 Бесконечно большие и бесконечно малые последовательности

    • 7.2.1 Свойства бесконечно малых последовательностей

  • 7.3 Сходящиеся и расходящиеся последовательности

    • 7.3.1 Свойства сходящихся последовательностей

  • 7.4 Монотонные последовательности

  • 7.5 Фундаментальные последовательности

Числовая последовательность — это последовательность элементов числового пространства.

Числовые последовательности являются одним из основных объектов рассмотрения в математическом анализе.

Определение

Пусть множество X — это либо множество вещественных чисел , либо множество комплексных чисел . Тогда последовательность элементов множества X называется числовой последовательностью.

Примеры

• Функция является бесконечной последовательностью целых чисел. Начальные отрезки этой последовательности имеют вид .

• Функция является бесконечной последовательностью рациональных чисел. Начальные отрезки этой последовательности имеют вид .

• Функция, сопоставляющая каждому натуральному числу одно из слов «январь», «февраль», «март», «апрель», «май», «июнь», «июль», «август», «сентябрь», «октябрь», «ноябрь», «декабрь» (в порядке их следования здесь) представляет собой последовательность вида . В частности, пятым членом x₅ этой последовательности является слово «май».

Операции над последовательностями

На множестве всех последовательностей элементов множества X можно определить арифметические и другие операции, если таковые определены на множестве X. Такие операции обычно определяют естественным образом, т. е. поэлементно.

Пусть на множестве X определена N-арная операция f:

Тогда для элементов , , …, множества всех последовательностей элементов множества Xоперация f будет определяться следующим образом:

Например, так определяются арифметические операции для числовых последовательностей.

Суммой числовых последовательностей (x_n) и (y_n) называется числовая последовательность (z_n) такая, что z_n = x_n + y_n.

Разностью числовых последовательностей (x_n) и (y_n) называется числовая последовательность (z_n) такая, что z_n = x_n − y_n.

Произведением числовых последовательностей x_n и y_n называется числовая последовательность (z_n) такая, что .

Частным числовой последовательности x_n и числовой последовательности y_n, все элементы которой отличным от нуля, называется числовая последовательность . Если в последовательности y_n на позиции всё же имеется нулевой элемент, то результат деления на такую последовательность всё равно может быть определён, как последовательность .

Конечно, арифметические операции могут быть определены не только на множестве числовых последовательностей, но и на любых множествах последовательностей элементов множеств, на которых определены арифметические операции, будь то поля или даже кольца.

Подпоследовательности

Подпоследовательность последовательности (x_n) — это последовательность , где (k_n) — возрастающая последовательность элементов множества натуральных чисел.

Иными словами, подпоследовательность получается из последовательности удалением конечного или счётного числа элементов.

Примеры

• Последовательность простых чисел является подпоследовательностью последовательности натуральных чисел.

• Последовательность натуральных чисел, кратных 12, является подпоследовательностью последовательности чётных натуральных чисел.

Свойства

• Всякая последовательность является своей подпоследовательностью.

• Для всякой подпоследовательности верно, что .

• Подпоследовательность сходящейся последовательности сходится к тому же пределу, что и исходная последовательность.

• Если все подпоследовательности некоторой исходной последовательности сходятся, то их пределы равны.

• Любая подпоследовательность бесконечно большой последовательности также является бесконечно большой.

• Из любой неограниченной числовой последовательности можно выделить бесконечно большую подпоследовательность, все элементы которой имеют определённый знак.

• Из любой числовой последовательности можно выделить либо сходящуюся подпоследовательность, либо бесконечно большую подпоследовательность, все элементы которой имеют определённый знак.

Предельная точка последовательности

Основная статья: Предельная точка

Предельная точка последовательности — это точка, в любой окрестности которой содержится бесконечно много элементов этой последовательности. Для сходящихся числовых последовательностей предельная точка совпадает с пределом.

Предел последовательности

Основная статья: Предел последовательности

Предел последовательности — это объект, к которому члены последовательности приближаются с ростом номера. Так в произвольном топологическом пространстве пределом последовательности называется элемент, в любой окрестности которого лежат все члены последовательности, начиная с некоторого. В частности для числовых последовательностей предел — это число, в любой окрестности которого лежат все члены последовательности начиная с некоторого.

Частичный предел последовательности — это предел одной из её подпоследовательностей. У сходящихся числовых последовательностей он всегда совпадает с обычным пределом.

Верхний предел последовательности — это наибольшая предельная точка этой последовательности.

Нижний предел последовательности — это наименьшая предельная точка этой последовательности.

Некоторые виды последовательностей

• Стационарная последовательность — это последовательность, все члены которой, начиная с некоторого, равны.

(x_n) стационарная

Ограниченные и неограниченные последовательности

В предположении о линейной упорядоченности множества X элементов последовательности можно ввести понятия ограниченных и неограниченных последовательностией.

• Ограниченная сверху последовательность — это последовательность элементов множества X, все члены которой не превышают некоторого элемента из этого множества. Этот элемент называется верхней гранью данной последовательности.

(x_n) ограниченная сверху

• Ограниченная снизу последовательность — это последовательность элементов множества X, для которой в этом множестве найдётся элемент, не превышающий всех её членов. Этот элемент называется нижней гранью данной последовательности.

(x_n) ограниченная снизу

• Ограниченная последовательность (ограниченная с обеих сторон последовательность) — это последовательность, ограниченная и сверху, и снизу.

(x_n) ограниченная

• Неограниченная последовательность — это последовательность, которая не является ограниченной.

(x_n) неограниченная

Критерий ограниченности числовой последовательности

Числовая последовательность является ограниченной тогда и только тогда, когда существует такое число, что модули всех членов последовательности не превышают его.

(x_n) ограниченная

Свойства ограниченных последовательностей

• Ограниченная сверху числовая последовательность имеет бесконечно много верхних граней.

• Ограниченная снизу числовая последовательность имеет бесконечно много нижних граней.

• Ограниченная последовательность имеет по крайней мере одну предельную точку.

• У ограниченной последовательности существуют верхний и нижний пределы.

• Для любого наперёд взятого положительного числа все элементы ограниченной числовой последовательности , начиная с некоторого номера, зависящего от , лежат внутри интервала .

• Если за пределами интервала лежит лишь конечное число элементов ограниченной числовой последовательности , то интервал содержится в интервале .

• Справедлива теорема Больцано — Вейерштрасса. Из любой ограниченной последовательности можно выделить сходящуюся подпоследовательность.

Бесконечно большие и бесконечно малые последовательности

• Бесконечно малая последовательность — это последовательность, предел которой равен нулю.

• Бесконечно большая последовательность — это последовательность, предел которой равен бесконечности.

Свойства бесконечно малых последовательностей

Бесконечно малые последовательности отличаются целым рядом замечательных свойств, которые активно используются в математическом анализе, а также в смежных с ним и более общих дисциплинах.

• Сумма двух бесконечно малых последовательностей сама также является бесконечно малой последовательностью.

• Разность двух бесконечно малых последовательностей сама также является бесконечно малой последовательностью.

• Алгебраическая сумма любого конечного числа бесконечно малых последовательностей сама также является бесконечно малой последовательностью.

• Произведение ограниченной последовательности на бесконечно малую последовательность есть бесконечно малая последовательность.

• Произведение любого конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность.

• Любая бесконечно малая последовательность ограничена.

• Если стационарная последовательность является бесконечно малой, то все её элементы, начиная с некоторого, равны нулю.

• Если вся бесконечно малая последовательность состоит из одинаковых элементов, то эти элементы — нули.

• Если (x_n) — бесконечно большая последовательность, не содержащая нулевых членов, то существует последовательность (1 / x_n), которая является бесконечно малой. Если же (x_n) всё же содержит нулевые элементы, то последовательность (1 / x_n) всё равно может быть определена, начиная с некоторого номера n, и всё равно будет бесконечно малой.

• Если (α_n) — бесконечно малая последовательность, не содержащая нулевых членов, то существует последовательность (1 / α_n), которая является бесконечно большой. Если же (α_n) всё же содержит нулевые элементы, то последовательность (1 / α_n) всё равно может быть определена, начиная с некоторого номера n, и всё равно будет бесконечно большой.

Сходящиеся и расходящиеся последовательности

• Сходящаяся последовательность — это последовательность элементов множества X, имеющая предел в этом множестве.

• Расходящаяся последовательность — это последовательность, не являющаяся сходящейся.

Свойства сходящихся последовательностей

• Всякая бесконечно малая последовательность является сходящейся. Её предел равен нулю.

• Удаление любого конечного числа элементов из бесконечной последовательности не влияет ни на сходимость, ни на предел этой последовательности.

• Любая сходящаяся последовательность элементов хаусдорфова пространства имеет только один предел.

• Любая сходящаяся последовательность ограничена. Однако не любая ограниченная последовательность сходится.

• Последовательность сходится тогда и только тогда, когда она является ограниченной и при этом её верхний и нижний пределы совпадают.

• Если последовательность (x_n) сходится, но не является бесконечно малой, то, начиная с некоторого номера, определена последовательность (1 / x_n), которая является ограниченной.

• Сумма сходящихся последовательностей также является сходящейся последовательностью.

• Разность сходящихся последовательностей также является сходящейся последовательностью.

• Произведение сходящихся последовательностей также является сходящейся последовательностью.

• Частное двух сходящихся последовательностей определено, начиная с некоторого элемента, если только вторая последовательность не является бесконечно малой. Если частное двух сходящихся последовательностей определено, то оно представляет собой сходящуюся последовательность.

• Если сходящаяся последовательность ограничена снизу, то никакая из её нижних граней не превышает её предела.

• Если сходящаяся последовательность ограничена сверху, то её предел не превышает ни одной из её верхних граней.

• Если для любого номера члены одной сходящейся последовательности не превышают членов другой сходящейся последовательности, то и предел первой последовательности также не превышает предела второй.

• Если все элементы некоторой последовательности, начиная с некоторого номера, лежат на отрезке между соответствующими элементами двух других сходящихся к одному и тому же пределу последовательностей, то и эта последовательность также сходится к такому же пределу.

• Любую сходящуюся последовательность (x_n) можно представить в виде (x_n) = (a + α_n), где a — предел последовательности (x_n), а α_n — некоторая бесконечно малая последовательность.

• Всякая сходящаяся последовательность является фундаментальной. При этом фундаментальная числовая последовательность всегда сходится (как и любая фундаментальная последовательность элементов полного пространства).

Монотонные последовательности

Основная статья: Монотонная последовательность

Монотонная последовательность — это невозрастающая, либо неубывающая последовательность. При этом предполагается, что на множестве, из которого берутся элементы последовательности, введено отношение порядка.

Фундаментальные последовательности

Основная статья: Фундаментальная последовательность

Фундаментальная последовательность (сходящаяся в себе последовательность, последовательность Коши) — это последовательность элементов метрического пространства, в которой для любого наперёд заданного расстояния найдётся такой элемент, расстояние от которого до любого из следующих за ним элементов не превышает заданного. Для числовых последовательностей понятия фундаментальной и сходящейся последовательностей эквивалентны, однако в общем случае это не так.

Литература

• В. А. Зорич Глава III. Предел. § 1. Предел последовательности // Математический анализ, часть I. — М.: Наука, 1981. — С. 104 — 114. — 544 с.

• Ю.С.Богданов - "Лекции по математическому анализу" - Часть 2 - Минск - Издательство БГУ им. В.И.Ленина - 1978.