Диференціальні рівняння першого порядку,
Реферат на тему:
Диференціальні рівняння першого порядку,
не розв’язані відносно похідної.
1. Основні поняття і означення, теорема про достатні умови існування і єдності розв’язку.
Диференціальне рівняння першого порядку, не розв’язані відносно похідної має вигляд
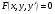 (5.1)
(5.1)
Найбільш часто зусрічаються диференціальні рівняння першого порядку 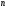 -ої степені.
-ої степені.
Означення 5.1. Функція 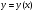 , визначена і
, визначена і
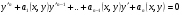 (5.2)
(5.2)
неперервнодиференційовна на 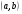 називається розв’язком Д.Р. (5.1), якщо вона після підстановки перетворює Д.Р. (5.1) в
називається розв’язком Д.Р. (5.1), якщо вона після підстановки перетворює Д.Р. (5.1) в
тотожність
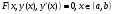
Означення 5.2. Будемо говорити, що рівняння 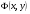 визначає розв’язок Д.Р.(5.1) в нормальній формі, якщо воно визначає
визначає розв’язок Д.Р.(5.1) в нормальній формі, якщо воно визначає 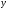 як функцію
як функцію 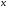 і вона являється розв’язком Д.Р.(5.1).
і вона являється розв’язком Д.Р.(5.1).
Означення 5.3. Рівняння 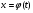 ,
, 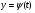 ,
,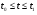 , визначає розв’язок Д.Р.(5.1) в параметричній формі, якщо
, визначає розв’язок Д.Р.(5.1) в параметричній формі, якщо
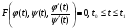
Криві на ел.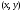 , які відповідають розв’язкам, будемо називати
, які відповідають розв’язкам, будемо називати 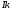
Задача Коші - задача знаходження розв’язків, які задовільняють умови 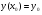 .
.
Означення 5.4. Говорять, що задача Коші для Д.Р.(5.1) з початковими умовами 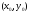 має єдиний розв’язок, якшо через
має єдиний розв’язок, якшо через 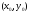 в достатньо малому околі її проходить стільки
в достатньо малому околі її проходить стільки 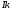 , скільки напрямків поля визначає Д.Р. в цій точці. В противному – не єдиний розв’язок.
, скільки напрямків поля визначає Д.Р. в цій точці. В противному – не єдиний розв’язок.
Теорема 5.1. (про існування і єдиність розв’язку задачі Коші).
Якщо функція 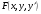 задовільняє наступним умовам:
задовільняє наступним умовам:
а) Являється визначеною і неперервною разом зі своїми ЧП в деякому замкненому околі т.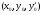 ;
;
б)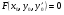 ;
;
в)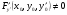 ;
;
то Д.Р.(1) має єдиний розв’язок 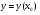 , визначений і неперервно диференційовний в околі т
, визначений і неперервно диференційовний в околі т 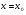 , задовільняючий умови
, задовільняючий умови 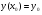 і такий, що
і такий, що 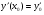
► Без доведення ◄
Припустимо, що розв’язуючи Д.Р.(1) відносно 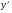 , ми знайдемо дійсні розв’язки
, ми знайдемо дійсні розв’язки
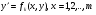 (5.3)
(5.3)
де 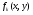 визначені в обл.
визначені в обл.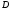 так, що маємо
так, що маємо 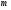 Д.Р. першого порядку, розв’язаних відносно
Д.Р. першого порядку, розв’язаних відносно 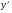 . Припустимо, що в
. Припустимо, що в 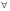 точці
точці 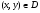 , напрямок поля, визначений кожним Д.Р. (5.3), різний. Так що
, напрямок поля, визначений кожним Д.Р. (5.3), різний. Так що 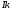 різних рівнянь не можуть дотикатися друг друга на
різних рівнянь не можуть дотикатися друг друга на 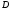 .
.
Нехай кожне Д.Р. (5.3) на 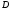 має загальний інтеграл
має загальний інтеграл
 (5.4)
(5.4)
Означення 5.5. Сукупність інтегралів (5.4) будемо називати загальним інтегралом Д.Р. (5.1) в обл. 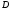 .
.
Інколи замвсть співвідношення (5.4) записують
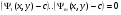 (5.5)
(5.5)
Якщо поле на 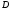 не задовільняє сказаному вище, тобто існує хоча б одна точка
не задовільняє сказаному вище, тобто існує хоча б одна точка 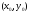 , в якій значення хоча б двох функцій
, в якій значення хоча б двох функцій 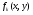 співпали, то
співпали, то 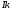 відповідаючі Д.Р. дотикаються друг друга в точці
відповідаючі Д.Р. дотикаються друг друга в точці 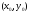 . Тому крім
. Тому крім 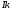 Д.Р. (5.3), будуть ще склеєні
Д.Р. (5.3), будуть ще склеєні 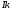 . Всі вони будуть входити в (5.4) або (5.5).
. Всі вони будуть входити в (5.4) або (5.5).
В загальному випадку Д.Р. (5.1) не удається розв’язати відносно 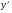 в елементарних функціях. В цих випадках шукають однопараметричне сімейство
в елементарних функціях. В цих випадках шукають однопараметричне сімейство 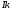 в вигляді
в вигляді
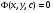 (5.6)
(5.6)
яке називається загальним інтегралом Д.Р. (5.1).
Якщо сімейство 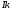 задано в вигляді
задано в вигляді
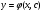 (5.7)
(5.7)
то воно називається загальним розв’язком Д.Р. (5.1)
Зауважимо, що в (5.6) можуть входити і розв’язки Д.Р. виду (5.3), коли 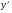 -комплексні. Ми таких Д.Р. не будемо розглядати, тому відповідні їм розв’язки треба виключати.
-комплексні. Ми таких Д.Р. не будемо розглядати, тому відповідні їм розв’язки треба виключати.
Сімейство 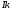 , заданих в параметричному вигляді
, заданих в параметричному вигляді
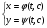 (5.8)
(5.8)
будемо називати загальними розв’язками Д.Р. в параметричній формі.
Означення 5.6. Розв’язок 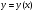 Д.Р. (5.1) будемо називати частинним розв’язком, якщо в кожній його точці задача Коші має єдиний розв’язок.
Д.Р. (5.1) будемо називати частинним розв’язком, якщо в кожній його точці задача Коші має єдиний розв’язок.
Означення 5.7. Розв’язок 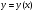 називається особливим розв’язком, якщо в кожній його точці порушується єдинність розв’язку задачі Коші.
називається особливим розв’язком, якщо в кожній його точці порушується єдинність розв’язку задачі Коші.
Аналогічно Д.Р., розв’язаним відносно 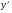 , Д.Р. (5.1) може мати розв’язки, які являються ні частинними, ні особливими.
, Д.Р. (5.1) може мати розв’язки, які являються ні частинними, ні особливими.
Аналіз частинних і особливих розв’язків для цих рівнянь більш складний. Зауважимо, що в випадку (5.3) розв’язок 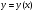 буде особливим, якщо буде особливим хоча б для одного з Д.Р. (5.3).
буде особливим, якщо буде особливим хоча б для одного з Д.Р. (5.3).
Приклад 5.1.
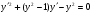 (5.9)
(5.9)
З (5.9) маємо: 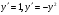
Тоді 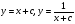 - загальний інтеграл.
- загальний інтеграл.
або 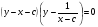 . Цей загальний інтеграл є накладенням сімейств двох
. Цей загальний інтеграл є накладенням сімейств двох 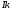 (мал. 5.1).
(мал. 5.1).
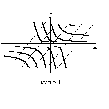
Розв’язок задачі Коші для Д.Р. (5.9) в кожній точці площіни 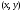 являється єдиним. В точці
являється єдиним. В точці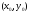 ми маємо два напрямки поля:
ми маємо два напрямки поля: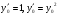 ; І через цю точку проходить два
; І через цю точку проходить два 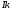
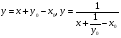 , якщо
, якщо 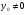 (5.11)
(5.11)
і 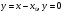 , якщо
, якщо 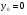 .
.
Розв’язки (10),(11) – частинні розв’язки. Особливих розв’язків немає.
2. Знаходження кривих, підозрілих на особливий розв’язок.
Припустимо, що Д.Р. (5.1) представлено в формі (5.3). При досліджені на особливий розв’язок рівнянь виду (5.3) ми прийшли до висновку, що ці розв’язки можливі на тих кривих, на яких 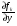 являється необмеженою. Але в переході від Д.Р. (5.1) до рівнянь (5.3) є недоцільність при визначені особливих розв’язків, так як
являється необмеженою. Але в переході від Д.Р. (5.1) до рівнянь (5.3) є недоцільність при визначені особливих розв’язків, так як 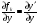 .
.
Дійсно, припустимо, що _____ похідні 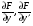 , тоді
, тоді
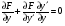 , звідки
, звідки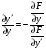 (5.12).
(5.12).
Припустимо, що  , тоді
, тоді 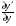 буде необмеженою при умові
буде необмеженою при умові
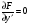 (5.13)
(5.13)
Таким чином, криві, підозрілі на особливий розв’язок будуть визначатися з системи
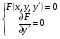 (5.14)
(5.14)
Розв’язок системи (5.14)
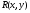 =0 (5.15)
=0 (5.15)
дискримінантна крива. Якщо вона задовільняє Д.Р. (5.1) і в кожній точці порушується єдність, то це буде особливий розв’язок.
Приклад 5.2.
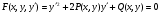 (5.16)
(5.16)
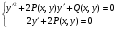 ,
, 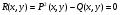 (5.17)
(5.17)
Співвідношення (5ю17) – дискримінантна крива рівняння (5.16). А на ній ми маємо не два а один напрямок поля 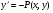 . В той же час – через неї може проходити не одна
. В той же час – через неї може проходити не одна 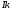 .
.
5.3. Загальний метод введення параметра.
Розглянемо Д.Р. (5.1). Припустимо, що воно допускає параметризацію
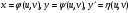 (5.18)
(5.18)
Так, що 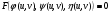 при всіх значеннях параметрів
при всіх значеннях параметрів 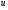 і
і 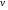 .
.
Використовуючи (5.18) і співвідношення 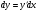 ми з Д.Р. (5.1) завжди зможемо привести до Д.Р., яке розв'язане Відносно похідної.
ми з Д.Р. (5.1) завжди зможемо привести до Д.Р., яке розв'язане Відносно похідної.
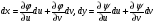
Тому
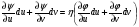
Візьмемо, наприклад, 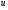 за незалежну змінну,
за незалежну змінну, 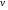 – за залежну, тоді прийдемо до Д.Р.
– за залежну, тоді прийдемо до Д.Р.
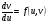 (5.19)
(5.19)
Якщо
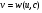 (5.20)
(5.20)
загальний розв'язок Д.Р. (5.19), то загальний розв'язок Д.Р. (5.1) можна отримати в параметричній формі.
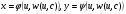 (5.21)
(5.21)
Розглянемо деякі частинні випадки:
А. Д.Р., розв'язані віднлсносно шуканої функції.
Це рівняння має вигляд
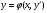 (5.22)
(5.22)
За параметри 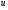 і
і 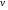 можна взяти
можна взяти 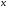 і
і 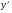 . Позначимо
. Позначимо 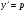 , тоді
, тоді
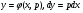 (5.23)
(5.23)
Маємо
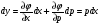
Звідки
 (5.24)
(5.24)
Нехай 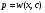 – загальний розв'язок Д.Р. (5.24), тоді
– загальний розв'язок Д.Р. (5.24), тоді 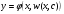 – загальний розв'язок Д.Р. (5.22).
– загальний розв'язок Д.Р. (5.22).
Д.Р. (5.24) може мати особливий розв'язок  , тоді Д.Р. (5.22) може мати особливий розв'язок
, тоді Д.Р. (5.22) може мати особливий розв'язок 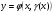 .
.
Б. Випадок, коли Д.Р. розв'язане відносно незалежної змінної.
Це рівняння має вигляд
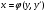 (5.25)
(5.25)
Інтегрується воно аналогічно Д.Р. (5.22). Покладемо 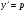 . Тоді
. Тоді
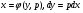
Використовуючи співвідношення 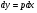 , отримаємо
, отримаємо
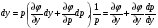 (5.26)
(5.26)
Якщо 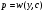 – загальний інтеграл Д.Р. (5.26), то
– загальний інтеграл Д.Р. (5.26), то
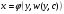 (5.27)
(5.27)
загальний інтеграл Д.Р. (5.25).
Якщо 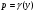 – особливий рощзв'язок Д.Р.(5.26), то
– особливий рощзв'язок Д.Р.(5.26), то  -може бути особливим розв'язком Д.Р. (5.25).
-може бути особливим розв'язком Д.Р. (5.25).
Розглянемо тепер більш прості випадки, коли рівняння можна проінтегрувати.
В. Рівняння Лагранжа.
Це рівняння має вигляд
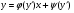 (5.28)
(5.28)
Воно інтегрується в квадратурах. Покладемо 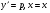 . Тоді
. Тоді
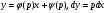 (5.29)
(5.29)
З (5.29) маємо
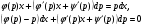 (5.30)
(5.30)
Д.Р. (5.30) лінійне по 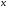
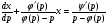 (5.31)
(5.31)
Нехай 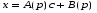 – розв'язок Д.Р. (5.31). Тоді загальний розв'язок рівняння Лагранжа запишемо в параметричній формі
– розв'язок Д.Р. (5.31). Тоді загальний розв'язок рівняння Лагранжа запишемо в параметричній формі
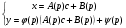 (5.32)
(5.32)
Особливі розв'язки можуть бути там, де
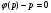 (5.33)
(5.33)
тобто
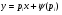 (5.34),
(5.34),
де 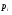 – корені рівняння (5.33).Розв'язок (5.34) може бути частинним або особливим.
– корені рівняння (5.33).Розв'язок (5.34) може бути частинним або особливим.
Г. Рівняння Клеро.
Це рівняння – частинний випадок рівняння Лагранжа, коли 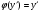 .
.
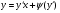 (5.35)
(5.35)
Покладемо 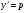 , тоді
, тоді
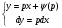 (5.36)
(5.36)
Використовуючи 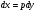 , отримаємо
, отримаємо
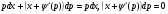 (5.37)
(5.37)
Рівняння (5.37) розпадається на два
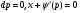 (5.38)
(5.38)
Перше рівняння дає 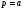 , підставляючи яке в (5.35) будемо мати загальний розав’язок
, підставляючи яке в (5.35) будемо мати загальний розав’язок
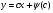 (5.39)
(5.39)
Друге - 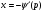 , разом з (5.35) утворює параметричні розв’язкі
, разом з (5.35) утворює параметричні розв’язкі
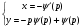 (5.40)
(5.40)
Розв’язок (5.40) являється особливим, так як він співпадає з _______. Дійсно
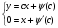
звідки
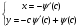 (5.41)
(5.41)
Дискримінантна крива (3.41) співпадає з розв’язком (3.40).
Приклад 5.3.
Розв’язати рівняння Лагранжа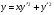 .
.
Покладемо 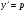 . Маємо
. Маємо 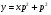 ,
,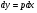
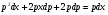 ,
, 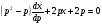
Отримали лінійне рівняння
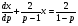
Його розв’язок
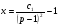 (5.42)
(5.42)
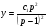 (5.43)
(5.43)
загальний розв’язок нашого рівняння в параметричній формі. Або, виключаючи 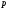 :
:
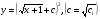 (5.44)
(5.44)
Знайдемо ті розв’язки, яким відповідають
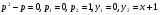
Перший розв’язок – офівфісобливий, другий – частинний.
Приклад 5.4.
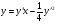
Це рівняння Клеро. Його загальний розв’язок –
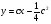
Запишемо дискримінантну криву
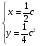
Звідки 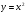 - особливий розв’язок, так як через цей розв’язок проходить ще розв’язок, який міститься в загальному при
- особливий розв’язок, так як через цей розв’язок проходить ще розв’язок, який міститься в загальному при 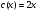 .
.
4. Неповні рівняння.
а). Д.Р. які містять тільки похідну.
Це рівняння вигляду
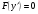 (5.45)
(5.45)
Рівняння (5.45) може мати скінчену або нескінчену кількість дійсних розв’язків.
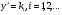 (5.46)
(5.46)
де 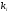 – деякі числа, задовільняючі функцію
– деякі числа, задовільняючі функцію 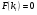 .
.
Інтегруємо (5.46)
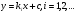 (5.47)
(5.47)
Так як 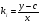 то
то
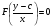 (5.48)
(5.48)
загальний інтеграл Д.Р. (5.45). Таким чином при таких припущеннях 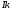 Д.Р. (5.45) є системою прямих ліній, які можна записати у вигляді (5.48). При цьому в (5.48) можуть входити комплексні розв’язки Д.Р.
Д.Р. (5.45) є системою прямих ліній, які можна записати у вигляді (5.48). При цьому в (5.48) можуть входити комплексні розв’язки Д.Р.
Приклад 5.5.
Розв’язати 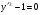 .
.
Згідно (5.48) 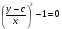 – загальний інтеграл. Однак у нього крім дійсного розв’язку
– загальний інтеграл. Однак у нього крім дійсного розв’язку 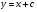 , входять розв’язки комплексного Д.Р.
, входять розв’язки комплексного Д.Р. 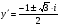
б) Д.Р., які не містять шуканої функції мають вигляд
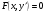 (5.49)
(5.49)
Якщо (5.49) можна розв’язати відносно похідної
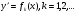 (5.50)
(5.50)
то
 (5.51)
(5.51)
являється загальним інтегралом Д.Р. (5.49).
Якщо ж розв’язати відносно 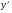 не можна, а допускається параметризація
не можна, а допускається параметризація
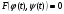 (5.52)
(5.52)
тобто
 (5.53)
(5.53)
Тоді загальний розв’язок знаходять в параметричній формі
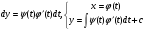 (5.54)
(5.54)
Якщо Д.Р. (5.49) має вигляд
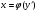 (5.55)
(5.55)
тоді це рівняння легко параметризується 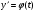 .В частинному випадку
.В частинному випадку 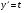 . Загальний розв’язок запишеться в формі
. Загальний розв’язок запишеться в формі
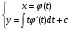 (5.56)
(5.56)
Приклад 5.6.
Зайти загальний розв’язок рівняння 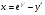 .
.
Вводимо параметризацію 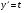 .
.
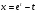 ,
, 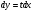 ,
, 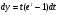
Маємо
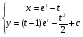
Загальний розв’язок в параметричній формі.
в) Д.Р., які не містятьнезалежної змінної.
Це рівняння вигляду
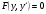 (5.57)
(5.57)
Якщо рівняння (5.57) розв’язане відносно 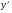 , тобто
, тобто
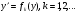 (5.58)
(5.58)
то
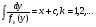 (5.59)
(5.59)
Являється загальним інтегралом Д.Р. (5.57). Особливими розв’язками можуть бути криві 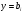 , де
, де 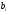 – корені рівняння
– корені рівняння 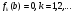 (або
(або  ).
).
Якщо Д.Р. (5.57) не можна розв’язати відносно 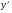 , але воно допускає параметризацію
, але воно допускає параметризацію
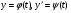 (5.60)
(5.60)
то
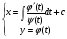 (5.61)
(5.61)
Загальний розв’язок Д.Р. (5.57) в параметричній формі.
Приклад 5.7.
Розв’язати 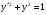 . Введемо параметризацію
. Введемо параметризацію 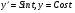 .
.
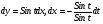
звідки
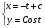
зашальний розв’язок нашого рівняння.
г) Узагальнено однорідні рівняння.
Д.Р. назвемо узагальнено однорідним, якщо ліва частина являється однорідною функцією аргументів 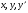 , яким відповідають величини
, яким відповідають величини  -го,
-го, 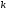 -го і
-го і 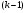 виміру, тобто
виміру, тобто
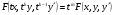 (5.62)
(5.62)
Зробимо заміну
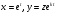 (5.63)
(5.63)
де 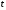 – нова незалежна змінна,
– нова незалежна змінна, – нова шукана функція. Маємо
– нова шукана функція. Маємо
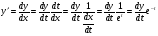
тобто 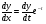 . З іншої сторони
. З іншої сторони
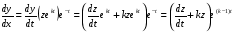 (5.64)
(5.64)
Підставимо (5.63),(5.64) в Д.Р. (5.1)
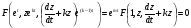
отримане рівняння
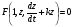 (5.65)
(5.65)
не містить незалежної змінної 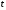 .
.

Нравится материал? Поддержи автора!
Ещё документы из категории математика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ