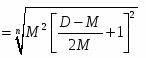
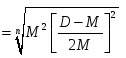
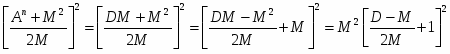
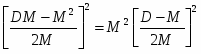
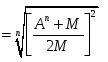
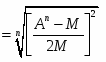
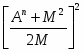
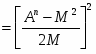
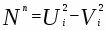
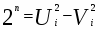
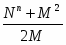
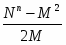Автор инженер-механик

Козий Николай Михайлович

ДОКАЗАТЕЛЬСТВО ВЕЛИКОЙ ТЕОРЕМЫ ФЕРМА

Великая теорема Ферма формулируется следующим образом: диофантово уравнение:

Аⁿ + Вⁿ = Сⁿ, (1)

где n- целое положительное число, большее двух, не имеет решения в целых положительных числах.

Суть великой теоремы Ферма не изменится, если уравнение (1) запишем следующим образом:

Аⁿ = Сⁿ - Вⁿ (2)

Для доказательства великой теоремы Ферма предварительно докажем вспомогательную теорему (лемму).

ЛЕММА: Любое натуральное число N>2 в любой степени равно разности квадратов двух натуральных чисел:

Nⁿ = U² – V² (3)

Уравнение (3) рассматриваем как параметрическое с параметром Nⁿ и неизвестными переменными U и V. Уравнение (3) запишем следующим образом:

Nⁿ = U² – V² = (U-V)∙(U+V) (4)

Пусть: U – V=M (5)

Тогда: U = V + M (6)

Из уравнений (4), (5) и (6) имеем:

Nⁿ=M∙ (V+M+V)=M∙(2V+M) = 2V∙M+M² (7)

Из уравнения (7) имеем:

Nⁿ - M²=2V∙M (8)

Отсюда: V = (9)

Из уравнений (6) и (9) имеем:

U = (10)

Из уравнений (9) и (10) следует, что необходимым условием для того чтобы числа U и V были целыми, является одинаковая четность чисел Nⁿ и M: оба числа должны быть четными или оба нечетными.

Из уравнений (9) и (10) также следует, что необходимым условием для того чтобы числа U и V были целыми, является делимость числа Nⁿ на число M , т. е. число M должно быть одним из сомножителей, входящих в состав сомножителей числа Nⁿ. Следовательно, должно быть:

Nⁿ =D·M (11)

где D - натуральное простое или составное число.

С помощью уравнений (9) и (10) определяются числа U и V, удовлетворяющие условиям уравнения (3).

Отсюда следует:

Следствие 1-е: Любое натуральное число N>2 в любой степени равно разности квадратов двух натуральных чисел.

Следствие 2-е: Число N=2 в степени n≥3 равно разности квадратов одной пары или нескольких пар натуральных чисел:

Следствие 3-е: Любое составное натуральное число в любой степени равно разности квадратов одной пары или нескольких пар натуральных чисел:

Доказательство теоремы Ферма

С учетом доказанной леммы можно записать:

Nⁿ = Аⁿ = U² – V² (12)

Допустим, что великая теорема Ферма имеет решение в натуральных числах. Тогда с учетом уравнений (2) и (11) должны выполняться равенства:

Nⁿ = D·M =Аⁿ = Сⁿ - Вⁿ = U² – V² (13)

Вⁿ = V² (14)

Cⁿ = U² = (15)

В (16)

C (17)

В соответствии с формулами (13) и (14) число Вⁿ равно:

Вⁿ = (18)

Из уравнения (15) с учетом уравнения (13) следует:

Cⁿ = (19)

Из уравнений (18) и (19) имеем:

В (20)

C (21)

Если допустить, что в соответствии с уравнением (20) В – целое число, то из уравнения (21) с очевидностью следует, что C – дробное число.

Таким образом, великая теорема Ферма не имеет решения в целых положительных (натуральных) числах.