Геометрические построения на местности с помощью циркуля и короткой градуированной веревки
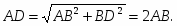
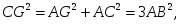
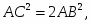







 XXXXI региональная научно-практическая конференция школьников и учащейся молодежи
XXXXI региональная научно-практическая конференция школьников и учащейся молодежи
Исследовательская работа по теме:
“Геометрические построения на местности с помощью циркуля и короткой градуированной веревки”
Секция: «математика»
Работа ученицы 8 класса
МОУ “Сорочинская СОШ”
Калачинского муниципального района Омской области
Искаревой Евгении
Руководитель:
Космачева Ольга Михайловна
учитель математики II категории
Калачинск, 2009 год
Оглавление
Введение
Задачи без использования градуированной веревки
Задача 1. Проложить прямую
Задача 2. Продолжить прямую
Задача 3. Найти точку пересечения двух прямых
Задача 4. Построение перпендикуляра к прямой
Задачи с использованием короткой градуированной веревки
Задача 5. Симметрия относительно точки (построение отрезка равного данному)
Задача 6. Построение прямой параллельной данной
Задача 7. Нахождение середины отрезка
Задача 8. Построение биссектрисы угла
Задача 9. Деление отрезка в данном отношении
Задача 10. Построения под заданным углом
Задача 11.Построение треугольника по двум сторонам и высоте к третьей стороне
Заключение
Литература
В школе мы довольно подробно изучаем геометрические построения с помощью циркуля и линейки, решая много различных задач.
Геометрические построения – это решение некоторых геометрических задач при помощи вспомогательных инструментов. А как решить такие же задачи на местности?
Ведь невозможно вообразить себе такой огромный циркуль, который мог бы очертить окружность школьного стадиона или линейку для разметки дорожек парка.
На практике картографам для составления карт, геодезистам для того, чтобы размечать участки на местности, например, для закладки фундамента дома, приходится использовать специальные методы.
Цель нашего исследования – изучить некоторые методы решения геометрических задач на местности, используя только циркуль (неотградуированное измерительное устройство – веревку) и короткую градуированную веревку, а также применить знания по геометрии к решению практических задач на местности.
Задачи:
рассмотреть актуальные задачи, связанные с геометрическими построениями на местности – провешиванием прямых, делением отрезков и углов, построение параллельных и перпендикулярных прямых и т.д.;
углубить имеющиеся знания по геометрии.
Гипотеза: мы предполагаем, что сможем решить некоторые геометрические задачи на построение, используя не классический набор инструментов (циркуль и линейку), а набор из циркуля и короткой градуированной веревки.
Задачи о построении на местности
Геометрия зародилась в глубокой древности, она изучает форму и взаимное расположение фигур в пространстве, которое нас окружает. В Древней Греции слова математика и геометрия были синонимами. Любые математические задачи, будь то доказательство свойств чисел или нахождение корней уравнений, решались геометрическими способами. Естественно, в такой ситуации важную роль приобрели задачи на построение. К построениям предъявлялись высокие требования точности, простоты, экономности. Самой совершенной линией на плоскости является окружность, а самой простой — прямая (ведь русское слово «простая» и означает «прямая», и «простить» значит «разрешить стоять прямо, не склонив головы»). Наиболее ценными считались построения, использующие только эти две линии. Поскольку прямую можно провести при помощи линейки (без делений), а окружность построить циркулем, то речь идет о задачах на построение с помощью циркуля и линейки. Циркуль позволяет не только построить окружность с указанным центром и радиусом, но отложить отрезок, равный данному, и выяснить, какой из имеющихся отрезков длиннее. С помощью линейки можно провести прямую через две данные точки. (Линейка с делениями, которой мы пользуемся, не годится для измерений длин отрезков, она дает приближенный результат — этого античные математики не могли допустить.)
Геометрические задачи на построение, возможно, самые древние математические задачи. Кому-то они сейчас могут показаться не очень интересными и нужными, даже надуманными. И в самом деле, где и зачем может понадобиться умение с помощью циркуля и линейки построить правильный семнадцатиугольник или треугольник по трем высотам, или даже просто построить прямую, параллельную данной? Современные технические устройства выполнят эти построения быстрее и точнее, чем любой человек, а также сделать и точные построения, которые невозможны, если использовать только циркуль и линейку.
И все же без задач на построение геометрия перестанет быть геометрией. Нельзя по-настоящему почувствовать геометрию, подружиться с ней, если " пройти мимо " этих кажущихся сейчас немного странными задач на построение.
В геометрии, как правило, точными считаются построения, выполненные с помощью циркуля и линейки. Эта традиция восходит к глубокой древности. Знаменитая геометрия Евклида (Евклид - древнегреческий ученый, 3-й век до н. э.) была основана на геометрических построениях, выполненных циркулем линейкой (без делений). Такой линейкой можно лишь проводить прямые линии (произвольные, через точку, через две точки). Нельзя откладывать отрезки данной длины, пользоваться обоими краями линейки. Циркулем можно строить окружности, сравнивать или откладывать данные отрезки на прямой.
Знание геометрии и умение применять эти знания на практике полезно в любой профессии. Традиционно построения на местности производят геодезисты для съемки плана земельного участка и строители для закладки фундаментов. Однако такие знания бывают довольно часто нужны и в других областях деятельности.
Можно подумать, что работа на местности ничем существенно не отличается от работы циркулем и линейкой на обыкновенной бумаге. Но это не так. На местности расстояния между точками довольно велики и нет таких линеек и циркулей, которые могли бы помочь нам. Да и вообще чертить на земле какие-либо линии затруднительно. Таким образом, построения на местности, основываясь на геометрических законах, имеют свою специфику:
- во-первых, все прямые не проводятся на земле, а прокладываются, т. е. отмечается на них, например, колышками, достаточно густая сеть точек. Обычно прокладку прямых на местности называют провешиванием прямых.
- Во-вторых, циркуля у нас фактически нет. Все, что остается от циркуля - это возможность откладывать окружности, используя только два колышка и натянутую нить между ними. Сами расстояния будут измеряться только короткой градуированной веревкой, что тоже усложняет задачу.
Как правило, участки местности представляют собой не идеально ровную поверхность, как тетрадный лист, на земле есть возвышения и углубления. Чтобы они не искажали геометрические образы прокладываемых линий, на местности строят не наклонные отрезки, а их проекции на горизонтальную плоскость – горизонтальные проложения. Их можно определить, зная угол наклон – угол, образованный линией местности и ее проекцией на горизонтальную плоскость. Эти углы измеряются специальными приборами эклиметрами.
Поскольку мы не ставим задачу изучения основ геодезии, то и не будем пользоваться никакими приборами - ни рулеткой, ни астролябией, ни экером, ни теодолитом. Работать так, конечно, трудно, но всё же, попытаемся решить предложенные ниже задачи только с помощью колышек, (неотградуированного измерительного устройства) – веревки и короткой градуированной веревки. Рассмотрим отдельно задачи, которые можно решить с помощью лишь циркуля (неотградуированного измерительного устройства – веревки) и задачи решаемые с помощью циркуля и короткой градуирован ной веревки. Очевидно, что в обоих случаях вспомогательные инструменты у нас разные, следовательно и решаемые задачи с имеющимся набором вспомогательных инструментов будут отличаться.
Задачи без использования градуированной веревки
Задача 1. Проложить прямую
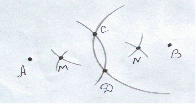
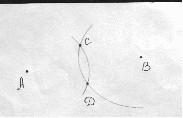
На местности колышками обозначены две удалённые друг от друга точки А и В. Как проложить через них прямую и, в частности, как можно устанавливать колышки на прямой между данными точками?
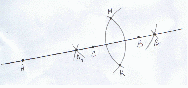
Решение: при решении данной задачи я буду пользоваться следующей аксиомой геометрии «Через любые две точки проходит прямая, и притом только одна». В этой задаче в качестве точек А и В выступают два колышка, через которые нужно провести прямую. (Задача имеет решение при условии, что длина данной веревки больше половины отрезка АВ).
Один конец нашей неотградуированной веревки привяжем к колышку обозначающего точку А, к другому концу привяжем колышек. Из точки А проводим полуокружность в направлении точки В. Аналогично, из точки В проведем полуокружность в направлении точки А. Так как веревка используется определенной длины, то данные полуокружности будет одного радиуса. При пересечении этих полуокружностей получатся две точки С и Д (обозначим их колышками).
Повторяя все выше сказанное с точками С и Д мы получаем две точки М и N лежащие на прямой АВ.
Таким образом можно построить множество точек между точками А и В.
Задача 2. Продолжить прямую
На местности колышками обозначены две удалённые друг от друга точки А и В. Как продолжить данную прямую в направлении точки А или точки В?
Решение: для решения данной задачи воспользуемся задачей 1 и построим хотя бы одну точку С лежащую между точками А и В, и принадлежащую прямой АВ.
Через точки В и С проводим две полуокружности до получения двух точек пересечения М и К.
Затем проведем те же построения, только с точками М и К. Таким образом получатся еще две точки А1 и В1, такие что, А1 лежит между точками А и В, а точка В1, как продолжение прямой АВ в направлении точки В.
Таким образом, можно получить множество точек прямой АВ.
Задача 3. Найти точку пересечения двух прямых
На местности колышками обозначены две точки (А и В) одной прямой и две точки (С и D) другой прямой. Как найти точку пересечения этих прямых?
Решение: данная задача сводится к построению двух различных прямых. Пользуясь задачей 1, 2 построим множество точек прямой АВ и множество точек прямой СD. Наша задача найти точку пересечения получившихся прямых АВ и CD.
Натянем веревку на ближайшие четыре колышка, как показано на рисунке, точка пересечения веревки и будет точкой пересечения прямых АВ и CD. В нашем случае это точка О.
Задача 4. Построение перпендикуляра к прямой
На местности обозначена данная прямая точками А и В. Как построить произвольный перпендикуляр к данной прямой?
Решение: для решения данной задачи воспользуемся задачей 1 и построим точки С и D.
Далее задача сводится к построению множества точек прямой СD, которая и будет являться перпендикуляром к прямой АВ.
Задачи с использованием короткой градуированной веревки
Задача 5. Симметрия относительно точки (построение отрезка равного данному)
На местности обозначены точки А и В. Как найти точку С, симметричную точке А относительно точки В?
Решение: построим некоторое число точек прямой АВ (задача 1) и с помощью короткой градуированной веревки найдем длину отрезка АВ (измерив расстояние между всеми построенными точками отрезка АВ).
Продолжим прямую АВ за точку В (задача 2) и отложим на ней точку С на расстоянии АВ от точки В. Для этого понадобится построить несколько точек прямой АВ в направлении точки В и отложив необходимое расстояние получим искомую точку С.
Задача 6. Построение прямой параллельной данной
На местности обозначены три данные точки: А, В и С, не лежащие на одной прямой. Через точку А проложите прямую, параллельную прямой ВС.
Решение: продолжим прямую АВ за точку В (задача 2) и отложим на ней точку D на расстоянии АВ от точки В(задача 5). Продолжим прямую СD за точку С и отложим на ней точку Е на расстоянии СD от точки С. Тогда отрезок АЕ будет параллелен отрезку ВС, являющемуся средней линией треугольника АDЕ, так как средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
Задача 7. Нахождение середины отрезка
Найдите середину отрезка АВ, заданного на местности двумя точками А и В.
Решение: возьмём какую-либо точку С, не лежащую на прямой АВ. Продолжим прямую CВ за точку С (задача 2) и отложим на ней точку D на расстоянии 2ВС от точки С (задача 5). Продолжим прямую АD за точку А (задача 2) и отложим на ней точку Е на расстоянии АD от точки А (задача 5). Искомая середина F отрезка АВ лежит на его пересечении с прямой ЕС. Действительно, отрезок СЕ параллелен отрезку AG - средней линии треугольника CDE (здесь G - середина отрезка CD). Так как, кроме того, BC = CG, то CF - средняя линия треугольника ABG, откуда AF = FB.
Задача 8. Построение биссектрисы угла
На местности обозначены три точки A, M и N, не лежащие на одной прямой. Проложите биссектрису угла MAN.
Решение: выберем на стороне данного угла точки В и С, а на другой - точки D и Е так, чтобы выполнялись равенства
AB = BC = AD = DE. (Воспользоваться задачей 5).
Найдём точку О пересечения прямых ВЕ и CD. (Воспользоваться задачей 3). Тогда прямая АО будет искомой биссектрисой, поскольку в равнобедренном треугольнике ACE биссектриса AF является одновременно и медианой, а значит, проходит через точку О пересечения медиан EB и CD.
Задача 9. Деление отрезка в данном отношении
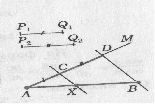
Отрезок, заданный на местности двумя точками А и В, требуется разделить в отношении, в котором находятся длины двух отрезков Р1Q1 и Р2Q2, заданных на местности точками Р1, Q1 и Р2, Q2, . Как это сделать?
Решение: построение точки Х, делящей отрезок АВ в отношении Р1Q1 и Р2Q2, произведём аналогично построению середины отрезка АВ, описанному в решении задачи 7. Отличие будет состоять в том, что мы проведем какой-нибудь луч АМ, не лежащий на прямой АВ, и на этом луче отложим последовательно отрезки АC и СD, равные отрезкам Р1Q1 и Р2Q2. Затем проведем прямую BD и прямую проходящую через точку С параллельно прямой BD. Она пересечет отрезок АВ в искомой точке Х.
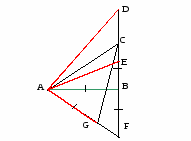
Задача 10. Построения под заданным углом
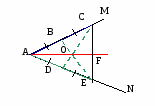
На местности обозначены точки А и В. Найдите точки C, D и E, для которых выполнены равенства BAC=45,BAD=6O, BAE=3O.
Решение: проложим перпендикуляр к прямой АВ (задача 4), пересекающий в какой–то точке луч АВ (задача 3). Будем считать для удобства, что эта точка пересечения и есть точка В. На перпендикуляре по разные стороны от точки В отложить точки С и F (задача 2), удалённые от точки В на расстояние АВ (задача 5). Тогда угол ВАС равен 45 (из равнобедренного прямоугольного треугольника АВС). На прямой AF отложим точку G на расстоянии АВ от точки А, а затем на прямой ВС отложим точку D на расстоянии CG от точки В. Тогда угол ВАD равен 6О, так как по теореме Пифагора для прямоугольного треугольников АВС, ACG и ABD имеют место равенства
Для построения точки Е теперь остаётся проложить биссектрису угла BAD.
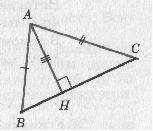
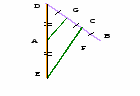
Задача 11. Построение треугольника по двум сторонам и высоте к третьей стороне
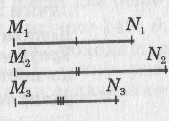
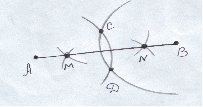
Постройте треугольник по двум сторонам и высоте к третьей стороне.
Даны три отрезка M1N1, M2N2, M3N3. Требуется построить такой треугольник АВС, у которого две стороны АВ и АС равны соответственно данным отрезкам M1N1 и M2N2, а высота АН равна отрезку M3N3.
Решение: построим прямоугольный треугольник АВН, у которого гипотенуза равна отрезку M1N1, а катет АН равен данному отрезку M3N3.
Затем проводим окружность радиуса M2N2 с центром в точке А. Одну из точек пересечения этой окружности с прямой ВН обозначим буквой С. Проведя отрезки ВС и АС, получим искомый треугольник АВС.
В настоящей работе рассмотрены наиболее актуальные задачи, связанные с геометрическими построениями на местности – провешиванием прямых, делением отрезков и углов, построение перпендикуляров, параллельных прямых и т.д. Рассмотрены задачи и даны их решения.
Приведенные задачи имеют значительный практический интерес, закрепляют полученные знания по геометрии и могут использоваться для практических работ. Ценно то, что для их решения не требуется знаний больших, чем в объеме 8 классов. Решение геометрических задач на построение ограниченным набором инструментов используемых в данной работе роднит их с классическими задачами на построение с помощью циркуля и линейки изучаемые в школьном курсе геометрии.
Таким образом, поставленная цель: изучение некоторых методов решения геометрических задач на местности с помощью циркуля и короткой градуированной веревки, а также применение знаний по геометрии к решению практических задач на местности нами достигнута.
Задачи поставленные в начале работы – выполнены, гипотеза подтвердилась и мы нашли решение некоторых геометрических задач на построение используя только циркуль и короткую градуированную веревку.
Нами были решены основные задачи на построение, на основе которых решаются и другие задачи на построение.
Кроме того, рассмотрев задачи на построение с помощью циркуля и линейки и сравнив их с задачами на построение с помощью циркуля и короткой градуированной веревки, мы можем предположить, что данные множества задач совпадают.
Решение: данная работа может служить учителям прекрасным пособием для проведения факультативных занятий по математики и учащимся для более глубокого изучения геометрии.
Боженкова Л.И. Алгоритмический подход к решению задач на построение (VII-VIII классы) – Омск: Изд-во областного ИУУ, 1989.
Геометрия, 7-9: учеб. для общеобразоват. учреждений / [Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др.]. – 18-е изд. – М.: Просвещение, 2008.
Час занимательной математики / под ред. Л.Я. Фальке. М.: Илекса; Народное образование; Ставрополь: Сервисшкола, 2003.
Шарыгин И.Ф., Егражиева Л.Н. Наглядная геометрия. М.: МИРОС, КПЦ “Марта”, 1992.

Нравится материал? Поддержи автора!
Ещё документы из категории математика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ