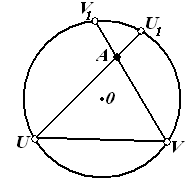
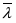
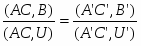
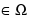
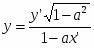
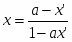
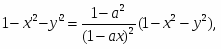
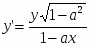
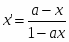
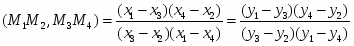
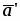
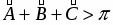
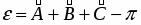
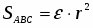
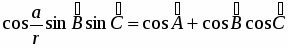
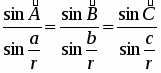
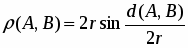
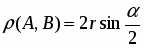
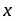
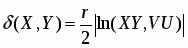
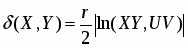
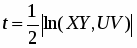
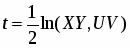
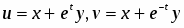
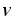
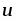
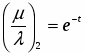
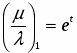
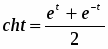
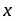
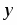
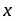
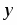
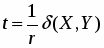
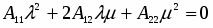
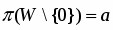
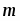
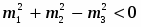
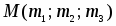
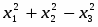
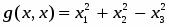
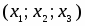
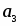
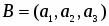
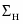
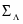
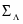
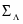
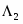
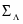
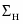
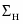
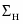
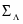
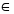
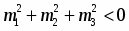
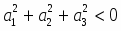
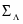
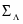
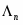
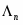
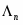
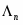
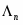
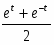
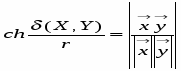
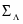
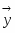
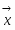
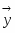
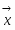
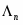
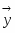
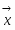
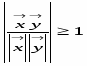
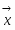
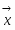
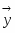
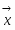
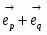
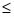
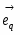
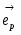
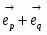
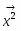
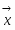
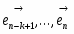
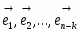
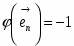
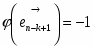
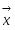
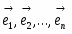
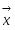
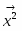
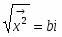
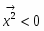
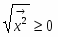
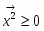
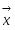
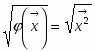
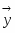
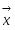
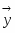
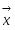
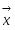
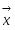
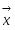
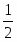
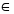
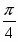
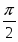
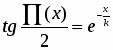
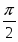
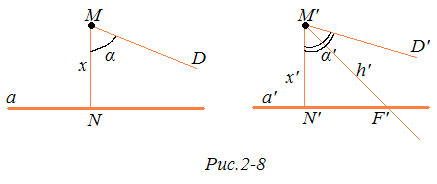
Тема: «Геометрия Лобачевского»

Выполнила: Зайнулина Г.

Г.Бишкек 2010

Н.И. Лобачевский и его геометрия

До начала XIX столетия ни одна из попыток доказательства V постулата не увенчалась успехом. Таким образом, проблема V постулата оставалась неразрешимой. И только в начале XIX в. были получены результаты, которые привели к решению этой проблемы. Основная заслуга в этом принадлежит знаменитому русскому ученому Н.И. Лобачевскому. Николай Иванович Лобачевский родился 2 декабря 1792 г. в Нижнем Новгороде (ныне г. Горький). Он окончил гимназию при Казанском университете, а затем и Казанский университет, после чего был оставлен там преподавателем. С 1816 г. Н.И. Лобачевский — профессор того же университета, с 1827 по 1846 г. — ректор университета. С 1846 по 1855 г.— помощник попечителя Казанского учебного округа. Н.И. Лобачевский скончался 24 февраля 1856 г. В течение первых лет преподавательской деятельности в Казанском университете Н.И. Лобачевский настойчиво пытался доказать V постулат. Неудачи этих попыток и попыток его предшественников привели его к выводу, что V постулат не может быть выведен из остальных постулатов геометрии. Чтобы это доказать, Н.И. Лобачевский построил логическую систему, в которой, сохраняя основные посылки Евклида, он отвергает V постулат и заменяет его противоположным допущением. Он пришел к выводу, что эта логическая схема представляет собой новую геометрию, которая может быть развита так же успешно, как и геометрия Евклида. 7 февраля (по старому стилю) 1826 г. Н. И. Лобачевский представил физико-математическому факультету Казанского университета доклад по теории параллельных под названием «Рассуждения о принципах геометрии». В 1829 г. в «Ученых записках Казанского университета» он поместил статью «О началах геометрии». Это была первая опубликованная работа по новой геометрии. В последующие годы Лобачевский издал еще ряд сочинений по геометрии. В этих сочинениях он первым отчетливо сформулировал и обосновал утверждение о том, что V постулат Евклида нельзя вывести из остальных аксиом геометрии. Лобачевский развивает свою геометрию на плоскости и в пространстве до тех же пределов, до каких была развита Евклидова геометрия, включая и формулы тригонометрии. Эту новую геометрию он назвал «воображаемой» (впоследствии ее стали называть геометрией Лобачевского или гиперболической геометрией). Открывая все новые и новые факты, Лобачевский не встретил в своей геометрии каких-либо логических противоречий. Исследования, проделанные им, привели к убеждению, что его логическая схема свободна от логических противоречий. Желая показать, что его геометрия никогда не приведет к противоречию, Лобачевский дает ее аналитическое исследование и решает проблему непротиворечивости своей геометрии вполне удовлетворительно для того времени. Лобачевский показал, что его геометрия может быть с пользой приложена в математическом анализе: он вычислил много интегралов, которые до него не поддавались вычислению. Примерно в одно время с Н.И. Лобачевским теорией параллельных прямых занимались великий немецкий математик Гаусс (1777—1855) и выдающийся венгерский математик Я. Бояи (1802— 1860). Но Гаусс не опубликовал ничего по теории параллельных, боясь, что его не поймут. После смерти Гаусса в его бумагах были найдены наброски отдельных наиболее простых теорем гиперболической геометрии. Я. Бояи опубликовал в 1832 г. (через три года после публикации Лобачевского и, не зная о последней) на латинском языке произведение «Приложение, излагающее абсолютно верное учение о пространстве, независимое от правильности или ложности XI аксиомы Евклида...». В этой работе, составившей приложение к математическому трактату его отца Фаркаша Бояи, Янош Бояи изложил ту же теорию, что и Лобачевский, но в значительно менее развитой форме. Результаты Лобачевского оказались настолько необычными для математиков, воспитанных на идеях геометрии Евклида, что не были поняты большинством из его современников (и даже академиком М.В. Остроградским — одним из крупнейших математиков XIX в.). Лишь после смерти Гаусса, когда была опубликована переписка Гаусса с некоторыми его друзьями-математиками, в которой содержались восторженные отзывы об исследованиях Лобачевского и Бояи, внимание математиков всего мира было привлечено к геометрии Лобачевского; появились многочисленные исследования, связанные с ней. Особое впечатление произвела работа Бельтрами «Опыт интерпретации неевклидовой геометрии», опубликованная в 1868 г. В ней были указаны поверхности, на которых в малом осуществляется двумерная геометрия Лобачевского. Наконец, в 1871 г. знаменитый немецкий математик Ф. Клейн (1849—1925) в работе «О так называемой неевклидовой геометрии» доказал непротиворечивость геометрии Лобачевского, чем устранил последние сомнения в ее правомерности. Исследования Лобачевского получили широкое признание после его смерти. Оказалось, что работы Лобачевского по геометрии представляют собой новый этап в развитии естествознания (недаром английский математик XIX в. Клиффорд называл Лобачевского Коперником геометрии). До Лобачевского евклидову геометрию считали единственно возможным учением о пространстве. Работы Лобачевского опровергли такой взгляд, привели к широким обобщениям в геометрии и их важнейшим приложениям в различных разделах математики, механики, физики и астрономии. Выше было отмечено, что с научной точки зрения систему аксиом и постулатов Евклида нельзя признать вполне удовлетворительной, так как у Евклида при изложении геометрии приходится в ряде случаев использовать утверждения, которые явно не высказаны и не доказаны. В конце 60-х годов прошлого столетия перед математиками возникла задача построить такую систему аксиом элементарной геометрии, на базе которой, опираясь лишь на законы логики, без ссылок на наглядность и очевидность можно было бы изложить всю геометрию. Эта задача стала особенно актуальной после того, как идеи Лобачевского получили всеобщее признание и появились работы Б. Римана по эллиптической геометрии. В конце XIX и в начале XX в. появились многочисленные работы по обоснованию геометрии ряда таких крупнейших математиков, как Паш, Пеано, Пиери, Гильберт, Вейль и др. Наиболее исчерпывающими явились работы Гильберта и Вейля. Эти исследования оказали большое влияние на формирование аксиоматического метода, который применяется во всех разделах современной математики. Книга Гильберта «Основания геометрии», вышедшая в 1899 г., сыграла существенную роль в этой серии исследований. Она в 1903 г. была удостоена Международной премии имени Н.И. Лобачевского. В ней впервые дан список аксиом, достаточный для логического построения евклидовой геометрии. Можно сказать, что с «Оснований геометрии» Гильберта начинается современный аксиоматический метод в математике. В следующих двух параграфах рассмотрим краткий обзор системы аксиом Гильберта.

Система аксиом Гильберта (обзор)

По Гильберту, предполагается, что даны три различных множества. Элементы первого множества называются точками, элементы второго множества — прямыми, а элементы третьего множества — плоскостями (основные объекты). Точки, прямые и плоскости обозначаются соответственно буквами А, В, С, ...; а, b, с, ...; α, β, γ, …. Элементы этих множеств находятся в определенных отношениях, которые называются: «принадлежность», «лежать между» и «конгруэнтность» (основные отношения). Природа основных понятий, т. е. основных объектов и основных отношений, может быть какой угодно, но они должны удовлетворять определенным аксиомам, которые перечислены ниже.

Список Гильберта содержит 20 аксиом, которые разделяются на пять групп.

Группа I. Аксиомы принадлежности.

Аксиомы этой группы определяют свойства взаимного расположения точек, прямых и плоскостей, выражаемые словом «принадлежит» (или «лежит на», «проходит через»). Группа I содержит следующие восемь аксиом.

I₁. Каковы бы ни были две точки А, В, существует прямая а, проходящая через эти точки.

I₂. Каковы бы ни были две точки А и В, существует не более одной прямой, проходящей через эти точки.

I₃. На каждой прямой лежат по крайней мере две точки. Существуют по крайней мере три точки, не лежащие на одной прямой.

I₄. Каковы бы ни были три точки А, В, С, не лежащие на одной прямой, существует плоскость α, проходящая через эти точки. На каждой плоскости лежит хотя бы одна точка.

I₅. Каковы бы ни были три точки, не лежащие на одной прямой, существует не более одной плоскости, проходящей через эти точки.

I₆. Если две точки А и В прямой а лежат в плоскости α, то каждая точка прямой а лежит в плоскости α.

В этом случае говорят, что прямая а лежит в плоскости α или плоскость α проходит через прямую а.

I₇. Если две плоскости α и β имеют общую точку А, то они имеют по крайней мере еще одну общую точку В.

I₈. Существуют по крайней мере четыре точки, не лежащие в одной плоскости.

Исходя из этих аксиом, можно доказать ряд теорем, большинство из которых в школьном курсе геометрии не доказываются, так как они наглядно очевидны. Перечислим некоторые из этих теорем.

1. Две прямые имеют не более одной общей точки.

2. Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих двух плоскостей.

3. Через прямую и не лежащую на ней точку, так же как через две пересекающиеся прямые, проходит одна и только одна плоскость.

4. На каждой плоскости существуют три точки, не лежащие на одной прямой.

Группа II. Аксиомы порядка.

Предполагается, что точка на прямой может находиться в известном отношении к двум другим точкам той же прямой; это отношение выражается словами «лежать между». Если точка В лежит между точкой А и точкой С, то мы запишем так: А — В — С. При этом должны быть удовлетворены следующие четыре аксиомы.

II₁. Если А — В — С, то А, В, С — различные точки одной прямой и С — В — А.

II_2.Каковы бы ни были две точки А и В, существует по крайней мере одна точка С на прямой АВ, такая, что А — В — С.

IIз. Среди любых трех точек прямой существует не более одной точки, лежащей между двумя другими.

По Гильберту, отрезком АВ (или ВА) называется пара точек A и B. Точки А и В называются концами отрезка, а любая точка, лежащая между ними,— внутренней точкой отрезка или просто точкой отрезка.

II₄ (аксиома Паша). Пусть А, В, С — три точки, не лежащие на одной прямой, а а — прямая в плоскости ABC, не проходящая ни через одну из точек А, В, С. Тогда если прямая а проходит через точку отрезка АВ, то она проходит также через точку отрезка АС или ВС.

Можно доказать, что утверждение, сформулированное в аксиоме Паша, верно и в том случае, когда точки А, В и С лежат на одной прямой. Нетрудно также доказать, что если прямая а пересекает какие-либо два из трех отрезков АВ, ВС и АС, то она не пересекает третий из этих отрезков.

С помощью аксиом групп I и II доказываются многие факты геометрии и вводится ряд основных определений. Прежде всего можно доказать, что между любыми точками существует по крайней мере одна точка, а отсюда легко прийти к выводу, что любой отрезок (а следовательно, и любая прямая) содержит бесконечное множество точек. Заметим, однако, что с помощью аксиом I и II групп нельзя доказать, что это множество несчетное. В дополнение к аксиоме IIз можно доказать, что из трех точек прямой всегда одна точка лежит между двумя другими.

Аксиомы групп I и II позволяют ввести такие важные понятия геометрии, как понятия полуплоскости, луча и полупространства. В качестве примера введем понятие полуплоскости. Предварительно докажем следующую теорему о полуплоскости.

Теорема. Прямая а, лежащая в плоскости α, разделяет множество точек, этой плоскости, не лежащих на прямой а, на два непустых подмножества так, что если точки А и В принадлежат одному подмножеству, то отрезок АВ не имеет общих точек с прямой а; если же эти точки принадлежат разным подмножествам, то отрезок АВ имеет общую точку с прямой а.

доказательство

Каждое из подмножеств точек, определяемых предыдущей теоремой, называется полуплоскостью плоскости α с границей а.

Группа III. Аксиомы конгруэнтности.

Предполагается, что отрезок (угол) находится в известном отношении к какому-то отрезку (углу). Это отношение выражается словом «конгруэнтен» и обозначается символом «». Должны быть удовлетворены следующие пять аксиом.

III₁. Если даны отрезок АВ и луч, исходящий из точки А', то существует точка В', принадлежащая данному лучу, такая, что АВ А'В'.

Можно доказать, что точка В' на данном луче единственная.

III₂. Если А'В' АВ и А"В" АВ, то А'В' А"В".

IIIз. Пусть А - В - С, А' - В' - С', АВ А'В' и ВС В'С'. Тогда АС А'С'.

III₄. Пусть даны hk и флаг (О', h', λ'). Тогда в полуплоскости λ’ существует один и только один луч k', исходящий из точки О', такой, что hk h'k'.

Каждый угол конгруэнтен самому себе.

III₅. Пусть А, В, С — три точки, не лежащие на одной прямой, и А', В', С' — тоже три точки, не лежащие на одной прямой. Если при этом

АВ А'В', АС А'С'. BAC В'А'С', то АВС А'В'С'.

Укажем некоторые теоремы, которые следуют из аксиом конгруэнтности.

1. Отношение конгруэнтности отрезков является отношением эквивалентности на множестве отрезков.

2. В равнобедренном треугольнике углы при основании равны.

По Гильберту, треугольник ABC называется конгруэнтным треугольнику

А'В'С' (∆АВС ∆А'В'С’), если АВ А'В', ВС В'С', СА С'А', АА АА', АВ АВ', АС АС'.

3. Первый, второй и третий признаки равенства треугольников.

4. Отношение конгруэнтности углов является отношением эквивалентности на множестве углов.

5. Внешний угол треугольника больше каждого угла треугольника, несмежного с ним.

6. В каждом треугольнике против большей стороны лежит больший угол и обратно: против большего угла лежит большая сторона."

7. Любой отрезок имеет одну и только одну середину.

8. Любой угол имеет одну и только одну биссектрису.

Группа IV. Аксиомы непрерывности.

IV₁ (аксиома Архимеда). Пусть АВ и CD — какие-нибудь отрезки. Тогда на прямой АВ существует конечное множество точек А₁, А₂, ..., А_n, таких, что выполняются условия: а) А — А₁ — A₂,, A₁ — А₂ — Аз, ..., A_{n - 2} — A_{n - 1} — A_n; б) АА₁ A₁A₂ ... А_{n – 1}A_n CD; в) А — В — A_n.

IV₂ (аксиома Кантора). Пусть на произвольной прямой а дана бесконечная последовательность отрезков А₁В₁, A₂B₂, …, из которых каждый последующий лежит внутри предыдущего и, кроме того, для любого отрезка CD найдется натуральное число п, такое, что А_nВ_n < CD. Тогда на прямой а существует точка М, принадлежащая каждому из отрезков данной последовательности.

Группа V. Аксиома параллельности.

Пусть а — произвольная прямая, а А — точка, не лежащая на этой прямой. Тогда в плоскости, определяемой точкой А и прямой а, существует не более одной прямой, проходящей через A и не пересекающей а.

В §3 мы доказали, что эта аксиома эквивалентна V постулату Евклида.

Аксиома Лобачевского. Параллельные прямые по Лобачевскому

Геометрия Лобачевского (или гиперболическая геометрия) основана на аксиомах групп I—IV абсолютной геометрии и на следующей аксиоме Лобачевского.

V*. Пусть а — произвольная прямая, а А — точка, не лежащая на этой прямой. Тогда в плоскости, определяемой точкой А и прямой а, существует не менее двух прямых, проходящих через точку А и не пересекающих прямую а.

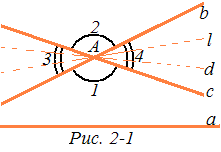
Ясно, что все определения и теоремы абсолютной геометрии имеют место и в геометрии Лобачевского. Из аксиомы V* непосредственно следует, что если даны произвольная прямая а и точка А, не лежащая на ней, то существует бесконечное множество прямых, проходящих через точку А и не пересекающих прямую а. В самом деле, по аксиоме V* существуют две прямые, которые обозначим через b и с, проходящие через точку А и не пересекающие прямую а (рис. 2-1). Прямые b и с образуют две пары вертикальных углов, которые на рисунке 2-1 обозначены цифрами 1, 2 и 3, 4. Прямая а не пересекает прямые b и с, поэтому все ее точки принадлежат внутренней области одного из четырех углов 1, 2, 3, 4, например внутренней области угла 1. Тогда, очевидно, любая прямая, проходящая через точку А и лежащая внутри вертикальных углов 3 и 4, не пересекает прямую а (например, прямые l и d на рис. 2-1).

В отличие от определения параллельных прямых по Евклиду в геометрии Лобачевского параллельными к данной прямой называются (только некоторые прямые из тех, которые не пересекают данную прямую. Чтобы ввести это понятие, условимся считать, что все прямые, рассматриваемые нами, являются направленными прямыми. Поэтому мы их будем обозначать двумя буквами, например UV, считая, что точка U предшествует точке V. Предполагается также, что точки U и V выбраны так, что рассматриваемые нами точки на этой прямой лежат между точками U и V.

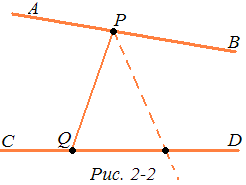
Введем следующее определение. Прямая АВ называется параллельной прямой CD, если эти прямые не имеют общих точек и, каковы бы ни были точки Р и Q, лежащие соответственно на прямых АВ и CD, любой внутренний луч угла QPB пересекает луч QD (рис. 2-2). Если прямая АВ параллельна прямой CD, то пишут так: AB||CD.

Имеет место следующий признак параллельности прямых.

Теорема 1. Если прямые АВ и CD не имеют общих точек и существуют точки Р и Q, такие, что Р є АВ и Q є CD, и любой внутренний луч угла QPB пересекает луч QD, то AB||CD.

доказательство

Из предыдущего изложения еще не следует, что существуют параллельные прямые по Лобачевскому. Докажем теорему о существовании параллельных прямых.

Теорема 2. Пусть АВ — произвольная направленная прямая, а М — точка, не лежащая на ней. Тогда в плоскости МАВ существует одна и только одна прямая CD, проходящая через точку М и параллельная прямой АВ, т. е. CD || AB.

доказательство

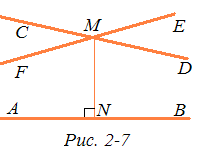
Пусть М — точка, не лежащая на прямой a, a MN — перпендикуляр, проведенный из точки М на прямую а. Выберем на прямой a две точки A и В так, чтобы А — N — В. Из теоремы 2 следует, что через точку М проходит единственная прямая CD, параллельная направленной прямой АВ, и единственная прямая EF, параллельная направленной прямой ВА (рис. 2-7).

В ходе доказательства теоремы 2 мы установили, что углы DMN и FMN острые, поэтому CD и EF—различные прямые. Докажем, что DMN = FMN. Пусть, напротив, DMN ≠ FMN, например DMN > FMN. Рассмотрим луч MF', симметричный лучу MF относительно прямой MN (луч MF' не изображен на рис. 2-7). Этот луч является внутренним лучом угла DMN. Так как MF не пересекает прямую АВ, то и MF' не пересекает эту прямую. Но это противоречит определению параллельности прямых CD и АВ.

Таким образом, через каждую точку М, не лежащую на данной прямой а, проходят две прямые, параллельные прямой а, в двух разных направлениях. Эти прямые образуют равные острые углы с перпендикуляром MN, проведенным из точки М к прямой а. Каждый из этих углов называется углом параллельности в точке М относительно прямой а.

Докажем, что величина угла параллельности вполне определяется расстоянием от точки М до прямой а. На этом рисунке 2-8 NMD — угол параллельности в точке М относительно прямой a, a N'M'D' — угол параллельности в точке М' относительно прямой а', α = NMD, x = MN, α' = N'M'D' , x' = M'N'. Докажем, что если х = х', то α = α' . Пусть, напротив, α' ≠ α, например α' > α. Тогда существует внутренний луч h’ угла N'M'D', такой, что угол между лучами M'N' и h' равен α . Луч h' пересекает прямую а' в некоторой точке F'. На прямой а от точки N отложим отрезок NF = N'F' так, чтобы точки F и D лежали в одной полуплоскости с границей MN. Получим треугольник MNF, равный треугольнику МN'F' (треугольник MNF на рис. 2-8 не изображен). Так как NMF = α, то лучи MD и MF совпадают. Мы пришли к выводу, что прямые MD и а пересекаются. Это противоречит определению параллельных прямых. Таким образом, α. = α'.

Итак, α — функция от х: α = П(х). Она называется функцией Лобачевского и играет существенную роль в гиперболической геометрии. Из предыдущего изложения ясно, что функция П(х) определена для каждого положительного х и что 0 < П(х) < .

Н.И. Лобачевский получил аналитическое выражение этой функции:

,

где k — некоторое положительное число.

Из этой формулы следует, что П(х)— монотонно убывающая непрерывная функция. Из этой формулы следует также, что П(х) принимает все значения, лежащие между О и . Другими словами, любой острый угол является углом параллельности в некоторой точке относительно данной прямой.

Таким образом, в геометрии Лобачевского существует зависимость между угловыми и линейными величинами; в этом существенное отличие геометрии Лобачевского от геометрии Евклида. Так, в геометрии Лобачевского нет подобия фигур; в частности, треугольники с соответственно равными углами равны. Еще одна особенность геометрии Лобачевского связана с единицей измерения длин. В геометрии Евклида существуют абсолютные константы угловых величин, например прямой угол или радиан, в то время как линейных абсолютных констант не существует. Для того чтобы длины отрезков выразить числами, необходимо выбрать единицу измерения длин. В качестве такой единицы может быть выбран произвольный отрезок. В противоположность этому в геометрии Лобачевского нет в этом необходимости, так как, имея естественную единицу измерения углов, можно условиться о выборе естественной единицы длин. Например, за единицу длины можно выбрать отрезок, которому соответствует угол параллельности, равный .

Треугольники и четырехугольники на плоскости Лобачевского

Все теоремы о треугольниках, которые в евклидовой геометрии доказывают без помощи аксиомы параллельности, имеют место также в геометрии Лобачевского. Подавляющее большинство теорем, известных читателю из курса средней школы, относится именно к этому типу. Теоремы о равнобедренных треугольниках, три признака равенства треугольников, теорема о внешнем угле треугольника, теоремы о соотношениях между сторонами и углами, теоремы о пересечении биссектрис внутренних углов треугольника и о пересечении медиан треугольника в одной точке — вот далеко неполный перечень теорем, которые имеют место как в евклидовой геометрии, так и в геометрии Лобачевского.

Но треугольники и четырехугольники на плоскости Лобачевского обладают рядом специфических свойств. Рассмотрим некоторые из них.

Теорема 1. Сумма углов любого треугольника меньше 2d.

доказательство

Следствие. Сумма углов трегольни- ка непостоянна, т. е. не одна и та же для всех треугольников.

доказательство

Теорема 2. Сумма углов выпуклого четырехугольника меньше 2d.

доказательство

Теорема 3. Если три угла одного треугольника соответственно равны трем углам другого треугольника, то эти треугольники равны.

доказательство

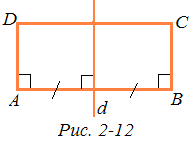
Выпуклый четырехугольник называется двупрямоугольником, если два угла, прилежащие к одной стороне, прямые. Если ABCD — двупрямоугольник с прямыми углами А и В, то сторона АВ называется основанием, а стороны AD и ВС — боковыми сторонами. Двупрямоугольник с равными боковыми сторонами называется четырехугольником Саккери. Рассмотрим некоторые свойства двупрямоугольников.

1°. Если ABCD — четырехугольник Саккери с основанием АВ, то С = D и каждый из углов С и D острый.

Рассмотрим симметрию относительно серединного перпендикуляра d к отрезку АВ (рис. 2-12). При этом, очевидно, точка А перейдет в точку В, а луч АD — в луч ВС (так как A = B = d).B силу равенства AD = ВС точка D перейдет в точку С и, следовательно, угол ADC — в угол BCD. Таким образом, C = D.

По теореме 2 А + В + С + D < 4d, поэтому С + D < 2d. Но так как С = D, то каждый из этих углов острый.

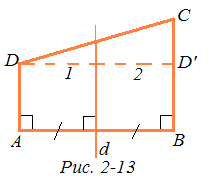
2°. Если в двупрямоугольнике ABCD с основанием АВ AD < ВС, то С < D.

Рассмотрим симметрию относительно серединного перпендикуляра d к отрезку АВ. При этом, очевидно, точка А перейдет в точку В, а точка D — в точку D' луча ВС (рис. 2-13). Так как АD < ВС и AD = BD', то BD' < ВС, поэтому D' — точка отрезка ВС. Четырехугольник ADD'В является четырехугольником Саккери, поэтому по свойству 1° 1 = 2. Но 1 < ADC, a 2> DCB (2 — внешний угол треугольника CDD'). Таким образом, DCB < АDC.

3°. Если в двупрямоугольнике ABCD с основанием АВ С < D, то AD < ВС.

Взаимное расположение двух прямых на плоскости Лобачевского

Лемма 1. Если АВ || CD, то существует ось симметрии прямых АВ и CD.

доказательство

Пользуясь этой леммой, легко доказать, что отношение параллельности направленных прямых удовлетворяет условию симметричности, т. е. справедлива теорема.

Теорема 1. Если АВ || CD, то CD || АВ.

доказательство

Теорема 2. Если АВ \\ EF, EF \\ CD и прямые АВ и CD не совпадают, то АВ || CD.

Две (ненаправленные) прямые а и b параллельными, если на этих прямых можно выбрать направления так, чтобы они были параллельны.

Две прямые на плоскости Лобачевского называются расходящимися (или сверхпараллельными), если они не пересекаются и не параллельны. Легко видеть, что через каждую точку М, не лежащую на прямой а, проходит бесконечное множество прямых, каждая из которых расходится с прямой а. В самом деле, пусть прямые CD и EF параллельны прямой а в разных направлениях (см. рис. 2-7). Тогда любая прямая, проходящая через точку М внутри вертикальных углов CMF и EMD, расходится с прямой а.

Таким образом, на плоскости Лобачевского в отличие от плоскости Евклида имеются три случая взаимного расположения двух прямых: прямые пересекаются, параллельны или расходятся.

Теорема 3. Две прямые, имеющие общий перпендикуляр, расходятся.

доказательство

Следствие. На плоскости Лобачевского не существует общего перпендикуляра двух параллельных прямых.

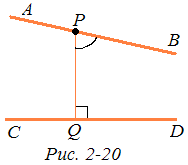
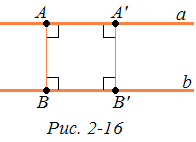
Заметим, что две прямые не могут иметь более чем один общий перпендикуляр. Действительно, если, например, прямые а и b имеют два общих перпендикуляра АВ и А'В' (рис. 2-16), то выпуклый четырехугольник ABB'А' имеет четыре прямых угла. Но это противоречит теореме 2 § 2 Гл. 2. Таким образом, если две прямые имеют общий перпендикуляр, то он единственный и по теореме 3 эти прямые расходятся. В заключение докажем, что на плоскости Лобачевского расстояние от переменной точки одной из двух параллельных или расходящихся прямых до другой прямой есть переменная величина. Для этого предварительно докажем следующую лемму.

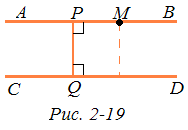
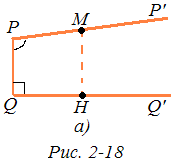
Лемма 2. Пусть лучи РР' и QQ' лежат в одной полуплоскости с границей PQ, PQQ' прямой, a QPP' прямой или тупой (рис. 2-18, а). Тогда если М — переменная точка луча РР', а Н — проекция этой точки на прямую QQ', то функция МН = f (MP) является монотонной, неограниченно возрастающей функцией.

доказательство

Пусть АВ и CD — расходящиеся прямые, a PQ — общий перпендикуляр этих прямых (рис. 2-19). Фигуры BPQD и APQC удовлетворяют условиям леммы2, поэтому согласно этой лемме расстояние от переменной точки М прямой АВ до прямой CD неограниченно возрастает, когда точка М удаляется от точки Р как в одном, так и в другом направлении. Образно говоря, расходящиеся прямые неограниченно «расходятся» друг от друга по мере удаления от общего перпендикуляра.

Пусть теперь АВ || CD, a PQ — перпендикуляр, проведенный из точки Р прямой АВ на прямую CD (рис. 2-20). Так как QPB острый, то смежный с ним QPA тупой. Фигура APQC удовлетворяет условиям леммы2, поэтому согласно этой лемме расстояние от перемен- ной точки М прямой АВ до прямой CD неограниченно возрастает, когда точка М удаляется от точки Р в сторону, противоположную направлению параллельности. Можно доказать, что если точка М удаляется от точки Р в сторону параллельности, то это расстояние стремится к нулю. Образно говоря, параллельные прямые, неограниченно удаляясь друг от друга в одном направлении, асимптотически приближаются в другом.

Окружность, эквидистанта и орицикл

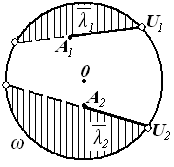
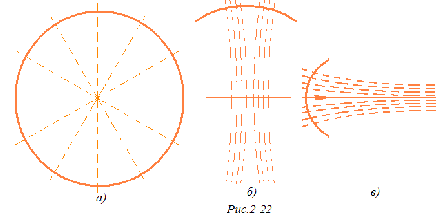
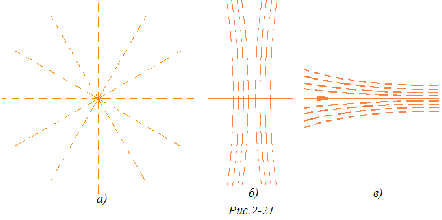
На плоскости Лобачевского существуют три различных типа пучков, а именно: а) пучок пересекающихся прямых, т. е. множество всех прямых плоскости, проходящих через одну точку - центр пучка (рис. 2-21, а); б) пучок расходящихся прямых, т. е. множество всех прямых плоскости, перпендикулярных к данной прямой (рис. 2-21, б); в) пучок параллельных прямых - множество прямых, состоящее из некоторой направленной прямой и всех направленных прямых, параллельных ей (рис. 2-21, в).

Ясно, что если задан пучок, то через любую точку плоскости (отличную от центра пучка пересекающихся прямых) проходит одна и только одна прямая пучка.

С каждым пучком прямых связаны определенные линии.

Окружность. Как известно из школьного курса геометрии, окружностью называется фигура, которая состоит из всех точек плоскости, равноудаленных от данной точки (центра окружности). Это определение относится к абсолютной геометрии, поэтому окружность линия как евклидовой плоскости, так и плоскости Лобачевского. Многие теоремы об окружности, известные учащемуся из курса геометрии средней школы, доказываются без помощи аксиомы параллельных, поэтому они справедливы и на плоскости Лобачевского. Прежде всего, отметим теорему о том, что любая прямая, лежащая в плоскости окружности, пересекается с ней не более чем в двух точках. Перечислим другие свойства окружности, которые относятся к абсолютной геометрии. При этом рассмотрим только те свойства, которые относятся к расположению точек окружности по отношению к пучку пересекающихся прямых с центром в центре окружности. Прямые этого пучка называются осями окружности.

1. Окружность симметрична относительно любой своей оси.

2. В каждой точке окружности существует касательная, которая перпендикулярна к оси, проходящей через точку касания.

Учитывая это свойство, мы можем говорить, что окружность пересекает свои оси под прямым углом или что окружность есть ортогональная траектория пучка прямых с центром в центре окружности (рис. 2-22, а).

Прямая АВ, где А а и В Ь, называется секущей равного наклона к прямым а и b, если отрезок АВ составляет с этими прямыми равные внутренние односторонние углы.

3. Прямая, содержащая хорду окружности, отличную от диаметра, является секущей равного наклона к осям, проходящим через концы хорды.

4. Серединный перпендикуляр к любой хорде окружности является ее осью.

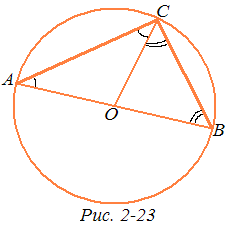
Не все свойства окружности, известные нам из школьного курса геометрии, имеют место на плоскости Лобачевского. Например, теорема о том, что угол, вписанный в окружность и опирающийся на диаметр, является прямым углом, неверна на плоскости Лобачевского. В самом деле, пусть угол АСВ, вписанный в окружность с центром О, опирается на диаметр АВ (рис. 2-23). Проведем радиус ОС и рассмотрим два равнобедренных треугольника ОАС и ОВС. Так как A = АСО и B = BCO, то A + В = АСО + ВСО =АСВ. Следовательно, σ_ABC = A + В + АВС = 2АСВ. Значит, АСВ = σ_ABC . Так как σ_ABC < 2d, то АСВ < d, т. е. АСВ — острый угол.

Эквидистанта. Эквидистантой называется фигура, которая состоит из всех точек полуплоскости с границей и, равноудаленных от этой прямой. Прямая и называется базой эквидистанты, а перпендикуляр, проведенный из любой точки эквидистанты на базу,— высотой. Высотой называется также длина h этого перпендикуляра.

С эквидистантой связан пучок расходящихся прямых — множество всех прямых, перпендикулярных к базе эквидистанты. Прямые этого пучка называются осями эквидистанты. Многие свойства эквидистанты аналогичны свойствам окружности.

Убедимся в том, что эквидистанта — кривая линия.

Теорема 1. Любая прямая, лежащая в плоскости эквидистанты, пересекается с эквидистантой не более, чем в двух точках.

доказательство

Рассмотрим другие свойства эквидистанты.

1. Эквидистанта симметрична относительно любой своей оси.

доказательство

2. В каждой точке эквидистанты существует касательная, которая перпендикулярна к оси, проведенной через точку касания.

доказательство

Учитывая это свойство, мы можем говорить, что эквидистанта является ортогональной траекторией пучка расходящихся прямых, перпендикулярных к базе эквидистанты (см. рис. 2-22, б).

Хордой эквидистанты назовем любой отрезок, соединяющий две точки эквидистанты.

3°. Любая прямая, содержащая хорду эквидистанты, является секущей равного наклона к осям, проходящим через концы хорды.

доказательство

4°. Серединный перпендикуляр к любой хорде эквидистанты является ее осью.

Орицикл. Прежде чем ввести понятие орицикла, докажем следующую лемму.

Лемма. Через каждую точку одной из двух параллельных прямых проходит одна и только одна секущая равного наклона к этим прямым.

доказательство

Пусть на плоскости задан пучок параллельных прямых. На множестве Ω всех точек плоскости введем бинарное отношение ∆ следующим образом. Будем говорить, что точки A и В находятся в отношении ∆, если они совпадают или прямая АВ является секущей равного наклона к прямым данного пучка, проходящим соответственно через точки А и В. Из этого определения непосредственно следует, что отношение ∆ удовлетворяет условиям рефлексивности и симметричности. Можно также доказать, что оно удовлетворяет условию транзитивности. Каждый элемент фактор-множества Ω/∆ называется орициклом (или предельной линией). Прямые данного пучка называются осями орицикла. Если задан пучок параллельных прямых, то через каждую точку А плоскости проходит один и только один орицикл, который представляет собой класс эквивалентности К_А по отношению ∆. Это множество состоит из точки А и всех таких точек X плоскости, что АХ -секущая равного наклона к прямым данного пучка, проходящим через точки А и X.

Если даны направленная прямая UV и на ней некоторая точка А, то тем самым однозначно определяется орицикл, проходящий через точку А с осью UV.

Свойства орицикла аналогичны свойствам окружности и эквидистанты.

Теорема 2. Любая прямая, лежащая в плоскости орицикла, пересекается с орициклом не более чем в двух точках.

доказательство

Орицикл симметричен относительно любой своей оси и является ортогональной траекторией пучка его параллельных осей (см. рис 2-22, в).

Любые два орицикла на плоскости Лобачевского равны.

Гиперболическое пространство

Пусть V — векторное пространство размерности п над полем R (в дальнейшем будем рассматривать значения п = 2,3). Зададим билинейную форму g: V V → R, такую, чтобы квадратичная форма φ () = g (,) была бы невырожденной квадратичной формой индекса k > 0. Число g (,)R назовем скалярным произведением векторов , и обозначим через ·или , а число длиной (нормой) вектора . Таким образом, если , то , а если , то , где b > 0 и i² = -1.

Векторное пространство V, в котором скалярное произведение определено при помощи указанной выше билинейной формы g, называется псевдоевклидовым векторным пространством индекса k.

В псевдоевклидовом пространстве скалярный квадрат вектора ≠ 0 может быть положительным, отрицательным или нулем. Например, если в базисе В = () квадратичная форма φ () имеет нормальный вид:

φ() = (x¹)²+ …+ (x^n-k)² – (x^n-k+1)² – … – (xⁿ)² , (1)

то, очевидно, для векторов базиса имеем:

, ,…, ,, …,.

Поэтому длина каждого из векторов равна единице; это единичные векторы. Каждый из векторов имеет мнимую длину i; назовем эти векторы мнимоединичными.

Вектор ≠ , для которого = 0, называется изотропным. Длины этих векторов равны нулю. Каждый из векторов , где и — векторы базиса В при р п — k, q > n — k, является изотропным, так как по формуле (1)

φ() = 1 – 1=0.

По-прежнему два вектора , будем называть ортогональными, если = 0. Векторы базиса В, в котором квадратичная форма имеет нормальный вид (1), попарно ортогональны, так как эти векторы попарно сопряжены относительно билинейной формы g(,).

Таким образом, базис В состоит из единичных и мнимоединичных попарно ортогональных векторов. Такой базис назовем ортонормированным. Так как индекс квадратичной формы φ () не зависит от способа приведения этой формы к нормальному виду, то все ортонормированные базисы псевдоевклидова векторного пространства V содержат одинаковое число мнимоединичных векторов; это число равно индексу пространства.

Пусть В — ортонормированный базис, а векторы и в этом базисе имеют координаты (xⁱ) и (уⁱ). Тогда = хⁱи у = yⁱ, поэтому

=x¹y¹ + x²y² + …+ x^n-ky^n-k – x^n-k+1y^n-k+1 - …- xⁿyⁿ . (2)

Докажем следующую теорему.

Теорема. В псевдоевклидовом векторном пространстве V индекса 1 для любых двух векторов мнимой длины справедливо неравенство

()²

причем знак равенства в этой формуле имеет место тогда и только тогда, когда векторы и коллинеарны.

доказательство

Следствие. В псевдоевклидовом векторном пространстве индекса 1 для любых двух векторов , мнимой длины справедливо неравенство

(3)

Пусть V — псевдоевклидово векторное пространство индекса размерности п + 1 над полем R (n = 2,3) и g (,) — билинейная форма, с помощью которой в пространстве V определено скалярное произведение. Мы будем рассматривать только автоморфизмы пространства V, т. е. такие линейные преобразования этого пространства, которые сохраняют скалярное произведение векторов (и значит, сохраняют длины векторов). Обозначим через Ω* множество всех векторов мнимой длины пространства V. Очевидно, что если φ — автоморфизм пространства V, то φ (Ω*) = Ω*.

Множество Е ≠ 0 называется п-мерным гиперболическим пространством Лобачевского (и обозначается через ), если задано отображение

π : Ω^*→E,

удовлетворяющее следующим аксиомам:

1) π— сюръекция;

2) π() = π() тогда и только тогда, когда и коллинеарны.

Систему аксиом 1—2 пространства Лобачевского обозначим через .

Элементы множества Е называются точками. Так же как и в случае проективного пространства, если X = π (), то будем говорить, что точка X порождена вектором .

Расстояние между точками X, Y , определяется следующим образом. Зададим положительное число r (одно и то же для данного пространства ). Если точки X, Y порождаются векторами , Ω*, то назовем расстоянием между этими точками неотрицательное число δ(X, Y), удовлетворяющее равенству

(4)

где ch t = - гиперболический косинус вещественной переменной t. Мы замечаем, что функция cht четная, определена на всей числовой оси и ее значения заполняют промежуток [1, + ∞]. Поэтому согласно формуле (3) расстояние между любыми двумя точками всегда существует и является положительным числом.

Число r > 0 называется радиусом кривизны пространства .

Правая часть формулы (4) показывает, что расстояние δ(X, Y) не зависит от выбора векторов, порождающих точки X и Y.

Всякий автоморфизм φ псевдоевклидова векторного пространства индуцирует некоторое преобразование f пространства по закону:

если

φ () = , то f(X) = X’.

Из формулы (4) следует, что преобразование f сохраняет расстояние между любыми двумя точками пространства . Такое преобразование f называется движением пространства .

Из определения пространства можно заключить, что гиперболические пространства Лобачевского и ' одной и той же размерности изоморфны. Следовательно, система аксиом категорична, теория T () однозначна и ее можно изучать, пользуясь любой интерпретацией.

Докажем, что система аксиом непротиворечива, если непротиворечива арифметика вещественных чисел. Для этого построим интерпретацию этой системы, используя множество R вещественных чисел. Для простоты изложения ограничимся случаем, когда п = 2, т. е. когда Е — плоскость Лобачевского.

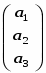
Вектором псевдоевклидова векторного пространства V индекса 1 размерности 3 назовем любой столбец вида , где а₁, a₂, a₃ — произвольные вещественные числа. Сумма векторов и умножение вектора на число вводятся обычным образом, т. е. как сумма столбцов и умножение столбца на число.

Скалярным произведением векторов и назовем число a₁b₁ + а₂b₂ - а₃b₃. Мы получили модель псевдоевклидова векторного пространства индекса 1 размерности 3. Очевидно, множество Ω* всех векторов мнимой длины состоит из тех и только тех векторов , для которых .

Введем следующее обозначение. Множество всех троек чисел вида km₁, km₂, km₃, где k — любое действительное число, отличное от нуля, а m₁, т₂, m₃ - фиксированные числа, не равные одновременно нулю, обозначим через < m₁, т₂, m₃>. ■

Точкой (т. е. элементом множества Е) назовем любое множество < m₁, т₂, m₃> при условии, что . Отображение π : Ω^*→E определим так: вектору поставим в соответствие точку < m₁, т₂, m₃> , такую, что (а₁, а₂, а₃) < m₁, т₂, m₃ >

В построенной интерпретации, очевидно, выполняются обе аксиомы системы .

Рассмотренное выше утверждение позволяет дать еще один способ доказательства независимости аксиомы параллельных от остальных аксиом евклидовой геометрии .

Система аксиом Гильберта евклидовой геометрии состоит из аксиом I, II, III, IV, V групп, где V — аксиома параллельных, эквивалентная (при сохранении аксиом I — IV) V постулату Евклида. Выше было доказано, что система аксиом непротиворечива, если непротиворечива арифметика вещественных чисел. В последующем мы ограничимся геометрией на плоскости, поэтому все системы аксиом будем рассматривать лишь для плоскости.

Рассмотрим систему аксиом ∑* = (\V) U V*. где V* — аксиома Лобачевского. Обозначим через систему аксиом 1—2 плоскости Лобачевского . Выше мы доказали, что эта система непротиворечива. При этом система аксиом категорична (все ее интерпретации изоморфны). Можно доказать (с помощью достаточно длинных рассуждений), что системы аксиом ∑* и эквивалентны.

Следовательно, для системы ∑* нашлась интерпретация — это та же интерпретация, что и интерпретация системы . Поэтому система аксиом ∑* (содержательно) непротиворечива. Но в таком случае из самого способа составления этой системы аксиом следует, что аксиома параллельных V не зависит от остальных аксиом (\ V) евклидовой геометрии.

Замечание. Так как аксиома параллельных V эквивалентна V постулату Евклида, то полученный результат можно еще сформулировать так: V постулат Евклида не зависит от остальных аксиом системы .

Модель Кэли — Клейна плоскости Лобачевского

Эта модель называется также моделью Кэли — Клейна. Ее построил английский математик Кэли, но он не понял, что введенная им геометрия в круге и есть геометрия Лобачевского; это сообразил позже, в 1870 г., немецкий математик Клейн.

1. Плоскость Лобачевского Λ₂ порождена множеством Q* векторов мнимой длины трехмерного псевдоевклидова пространства V (индекса 1). Скалярное произведение векторов пространства V определяется при помощи заданной билинейной формы g(х, у), такой, что g(x, х) — невырожденная квадратичная форма индекса 1.

Рассмотрим проективную модель плоскости Λ₂. На проективной плоскости Р₂, порожденной векторным пространством V, квадратичная форма g(х, х) определяет линию второго порядка Q : Ф (X) = 0, где Ф (X) = g(х, х), и вектор порождает точку XP₂. При этом на плоскости Р₂ рассматриваются не любые проективные преобразования, а только те, которые порождены автоморфизмами псевдоевклидова векторного пространства V. Такие проективные преобразования образуют стационарную подгруппу Н_Q кривой второго порядка Q.

Пусть — ортонормированный базис пространства V, причем — мнимоединичный вектор. Если в этом базисе вектор имеет координаты, то, очевидно . Базис В порождает проективный репер R = (А₁, А₂, A₃, E) плоскости Р₂. В этом репере в силу предыдущего равенства линия Q определяется уравнением

.

Следовательно, Q — овальная линия второго порядка.

Напомним, что точкаявляется внутренней точкой относительно линии Q тогда и только тогда, когда . Это означает, что точка М порождена вектором мнимой длины, т. е. .

Таким образом, при отображении определяющем проективную плоскость Р₂, множество (*)=Λ₂ есть множество точек, внутренних относительно овальной линии Q.

Так как при отображении  аксиомы Σ_Λ выполняются, то множество (*)=Λ₂ точек, внутренних относительно кривой Q, является моделью плоскости Лобачевского. Линия второго порядка Q называется абсолютом плоскости Лобачевского Λ₂.

2. Выясним, как изображаются прямые, отрезки, лучи, полуплоскости и углы на модели Кэли — Клейна.

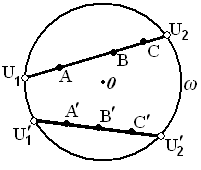
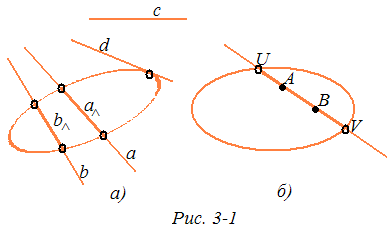
Пусть W — двумерное подпространство пространства V и ' =W∩*≠. Тогда фигура (*) называется прямой плоскости Лобачевского Λ₂. Так как есть прямая на проективной плоскости Р₂, то прямая плоскости Лобачевского является пересечением прямой а с внутренней областью абсолюта . На рисунке 3-1, а проективные прямые а и b определяют прямые а_Λ и b_Λ плоскости Лобачевского, которые представляют собой хорды (без концов) абсолюта  и выделены жирной линией. На том же рисунке проективные прямые с и d не определяют прямых на плоскости Λ₂, так как на них нет точек, внутренних относительно абсолюта. Таким образом, проективная прямая и определяет прямую и_Λ на плоскости Λ₂ тогда и только тогда, когда на ней лежит хотя бы одна внутренняя точка относительно абсолюта . Другими словами, проективная прямая и определяет прямую u_Λ на плоскости Λ₂ тогда и только тогда, когда она пересекает абсолют в двух вещественных точках U и V. Прямую и_Λ будем обозначать через UV или VU (рис. 3-1, б).

Мы видим, что прямыми плоскости Лобачевского являются хорды (без концов) абсолюта. Любые две точки А и В плоскости А₂, лежащие на прямой UV, не разделяют пару точек U, V (рис. 3-1, б), т. е. (UV, АВ)> 0.

Введем понятие «лежать между» для трех точек прямой на модели Кэли — Клейна. Предварительно докажем следующую теорему.

Теорема. Пусть А, В и М — три точки на прямой UV плоскости А₂. Если (АВ,MU) <0, то и (АВ, MV) <0.

доказательство

Пусть А и В — две точки плоскости Λ₂, лежащие на прямой UV. Будем говорить, что точка М прямой UV лежит между точками А и В (и писать: А —М — В), если пара точек А, В разделяет пару точек М, U (или пару точек М, V), т. e.(AB,MU) < 0 (или (АВ, MV) < 0).

Легко видеть, что это определение не зависит от порядка, в котором берутся точки А и В. В самом деле, так как (АВ, MU) = (BA,MU)^-1, то если А — М — В, то В — М — А. Нетрудно убедиться в том, что на модели Кэли — Клейна выполняются и все другие аксиомы группы II Гильберта.

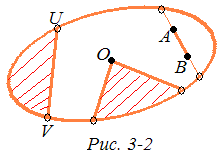
Далее, обычным путем определяются понятия отрезка, многоугольника, луча, угла и полуплоскости. На рисунке 3-2 изображены отрезок АВ и угол О, внутренняя область угла О заштрихована. На этом же рисунке одна из полуплоскостей с границей UV заштрихована.

3. Выясним теперь, как интерпретируется на модели Кэли — Клейна расстояние между двумя точками. Для этого воспользуемся общей формулой расстояния между двумя точками.

Пусть X, Y — две точки плоскости ₂.

Найдем векторы, порождающие точки пересечения прямой XY с абсолютом Q. Для этого записываем уравнение проективной прямой XY в параметрическом виде и находим отношение (или ) из уравнения точек пересечения линии с прямой . Если точки X, Y порождены векторами и , то уравнение принимает вид:

(2)

Учитывая, что векторы, мнимой длины, мы можем их нормировать так, чтобы , где r > 0 — тоже число, что и в формуле (4) §1 Гл.3. Из этой формулы находим

.

Уравнение (2) принимает вид:

, (3)

где берется знак «плюс» в случае < 0 и знак «минус» в случае >0.

Рассмотрим случай >0. Учитывая, что , из уравнения (3) находим:

и .

Следовательно, если U и V — точки пересечения прямой XY с линией Q, то векторы и , порождающие эти точки, имеют вид:

.

Отсюда находим (XY, UV) = е^2t, поэтому . Правая часть этого равенства меняет знак при перемене мест точек U и V. Но так как t> 0, то надо считать, что

.

Таким образом,

(4)

Так как (ХV, UV) = (XY, VU)^-1, то расстояние между точками X, Y, вычисленное по этой формуле, не зависит от порядка, в котором берутся точки U и V в формуле (4). Таким образом, формулу (4) можно записать также следующим образом:

(4’)

В случае < 0 мы получаем те же формулы (4) или (4').

4. Трехвершинник A₁A₂A₃ называется автополярным трехвершинником второго рода для овальной линии второго порядка Q, если точки A₁, A₂ лежат на этой линии, а прямые A₁A₃ и А₂Аз являются касательными к ней в точках А₁ и А₂ соответственно. Следовательно, каждая из сторон такого трехвершинника является полярой одной из его вершин, а именно: А₁А₃ — поляра точки А₁, А₂А₃ — поляра точки А₂ и А₁А₂ — поляра точки А₃ (отсюда и термин «автополярный») .

Пусть A₁A₂A₃ — автополярный трехвершинник второго рода для овальной линии Q. Выберем проективный репер R — (A₁,A₂,A₃, E), где EQ . Тогда нетрудно заметить, что в таком репере кривая Q определяется уравнением

.

Рассмотрим стационарную подгруппу H_Q абсолюта Q в проективной группе плоскости Р₂. Если f  H_Q, то f индуцирует некоторое преобразование f_Λ на плоскости Λ₂, так как в преобразовании f внутренняя область абсолюта переходит в себя. Формула (4) показывает, что преобразование f _Λ сохраняет расстояние между любыми двумя точками плоскости Λ₂, поэтому f_Λ называется движением плоскости Λ₂. Очевидно, множество всех движений плоскости Λ₂ образует группу, которая индуцируется группой H_Q.

Две фигуры F, F' Λ₂ называются равными (конгруэнтными), если они H_Q – эквивалентны.

Каждое преобразование fH_Q переводит любой автополярный трехвершинник второго рода для абсолюта Q в автополярный трехвершинник второго рода для этого же абсолюта. Поэтому движение f_Λ, которое индуцируется преобразованием f, однозначно определяется заданием упорядоченной пары реперов: R=(A₁, A_2, A₃, Е), R'=(A'₁, A'_2, A'₃, Е'), где A₁A₂A₃ и A'₁A'₂A'₃— автополярные трехвершинники второго рода для абсолюта Q и Е, Е'Q. Обратно: пусть (A₁, A_2, A₃, Е) и (A'₁, A’_2, A’₃, Е') — два репера, удовлетворяющие вышеуказанным условиям. Тогда проективное преобразование f, которое переводит репер R в репер R', принадлежит стационарной подгруппе H_Q, поэтому порождает некоторое движение f _Λ. Мы доказали следующее утверждение: каковы бы ни были два репера R=(A₁,A_2,A₃,Е) и R'=(A'₁, A'_2, A'₃, Е'), где A₁A₂A₃ и A'₁ A'₂ A'₃— автополярные трехвершинники второго рода для абсолюта Q, а Е, Е'Q, существует одно и только одно движение f_Λ плоскости Λ₂, которое индуцируется проективным преобразованием f e H_Q, переводящим репер R в репер R'.

Замечание. Заметим, что плоскость Лобачевского может быть реализована «в малом» на поверхности постоянной отрицательной кривизны, т. е. на псевдосфере. Пусть F— гладкая элементарная поверхность достаточно малого размера. (Это значит, что вся она лежит в некоторой -окрестности одной из своих точек при достаточно малом .) Тогда геодезические линии поверхности F являются аналогом прямых линий на плоскости. Если F лежит на псевдосфере, то (как и на плоскости Лобачевского) сумма углов геодезического треугольника поверхности F меньше . Поэтому можно сказать, что на псевдосфере реализуется «в малом» геометрия Лобачевского.

О свойствах параллельных и расходящихся прямых на плоскости Лобачевского

1. Так как все интерпретации системы аксиом Σ_Λ2 плоскости Лобачевского изоморфны, то всю геометрию  (Σ_Λ2) можно получить с помощью одной из них, например, с помощью интерпретации Кэли — Клейна.

Возьмем на плоскости Λ₂ прямую UV и точку А, не лежащую на этой прямой (рис.3-3). Через точку А проведем прямые U'V и UV’. Рассмотрим прямые UV’ и U'V. Эти прямые не пересекаются на плоскости Лобачевского Λ₂. Но для произвольной точки СUV любой внутренний луч AD угла CAV пересекает луч CV. Следовательно, по определению параллельных прямых на плоскости Λ₂ (§1 Гл.2) прямая U'V параллельна прямой UV. Мы знаем, что отношение параллельности двух прямых на плоскости Лобачевского симметрично (§3 Гл.2, теорема 1). Следовательно, и прямая UV параллельна прямой U'V. Мы скажем, что эти прямые параллельны в направлении V. Точно так же убеждаемся, что прямые VU и VU параллельны в направлении U.

Таким образом, в интерпретации Кэли — Клейна параллельные прямые изображаются хордами абсолюта Q, имеющими общий конец.

Прямые UV и MN на рисунке 3-3 расходятся. Можно сказать, что расходящиеся прямые изображаются такими хордами абсолюта, что содержащие их проективные прямые пересекаются в точке, внешней относительно абсолюта.

2. В §3 Гл.2 мы изучили некоторые свойства параллельных прямых на плоскости Лобачевского. Рассмотрим еще два свойства, для доказательства которых воспользуемся моделью Кэли — Клейна, так как на этой модели эти свойства доказываются значительно проще.

Теорема 1. На плоскости Лобачевского отношение параллельности прямых в одном и том же направлении транзитивно.

доказательство

Теорема 2. Пусть на плоскости Лобачевского даны две пары параллельных прямых: прямые UV, U\V, параллельные в направлении V, и прямые U'V, U\V, параллельные в направлении V (рис. 3-4). Тогда существует движение, которое переводит первую пару параллельных прямых во вторую.

доказательство

3. Докажем теорему о перпендикулярных прямых на модели Кэли — Клейна.

Теорема 3. Прямые АВ и CD на плоскости А₂ перпендикулярны тогда и только тогда, когда они изображаются хордами абсолюта Q, лежащими на проективных прямых, каждая из которых проходит через полюс другой.

доказательство

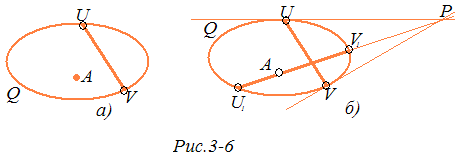
Замечание. Используя доказанную теорему, легко решить следующую задачу на модели Кэли — Клейна. На плоскости Λ₂ даны прямая UV и точка А, не лежащая на ней (рис.3-6, а). Построить прямую, проходящую через точку А и перпендикулярную к прямой UV. На плоскости Р₂ строим полюс Р проективной прямой UV и проводим проективную прямую АР, которая пересекает абсолют Q в точках U₁, V₁ (рис. 3-6, б). По доказанной теореме хорда U₁, V₁ является искомой прямой плоскости Λ₂.

4. Мы отметили, что в интерпретации Кэли — Клейна две расходящиеся прямые изображаются такими хордами абсолюта, что проективные прямые, содержащие эти хорды, пересекаются во внешней точке относительно абсолюта. Выше было доказано, что если две прямые имеют общий перпендикуляр, то они расходятся (§3 Гл.1, теорема 3). Докажем обратную теорему.

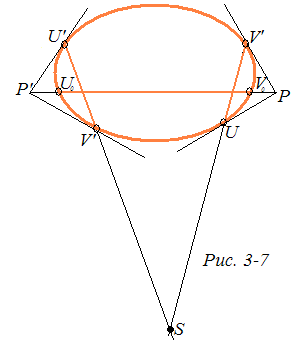
Теорема 4. Две расходящиеся прямые UV и U'V' имеют общий перпендикуляр, и притом единственный.

Теорема 4. Две расходящиеся прямые UV и U'V' имеют общий перпендикуляр, и притом единственный.

Пусть Р и Р' — полюсы проективных прямых UV и U'V’ соответственно, a S — точка пересечения проективных прямых UV и U'V’ на проективной плоскости Р₂ (рис. 3-7). Прямая РР' проходит через полюсы прямых UV и U'V’, поэтому по теореме взаимности поляритета проективные прямые UV и U'V’ проходят через полюс прямой РР'. Но UV∩U'V’=S, следовательно, S — полюс прямой РР'. По условию S — внешняя точка относительно абсолюта, и, значит, ее поляра — прямая РР' пересекает абсолют в двух точках U₀ и V₀.

Так как проективная прямая U₀V₀ проходит через полюсы Р и Р' прямых UV и U'V (рис.3-7), то по теореме 3 U₀V₀UV и U₀V₀U’V’, т. е. прямая U₀V₀ на плоскости Λ₂ является общим перпендикуляром двух расходящихся прямых UV и U'V’. Такая прямая единственная, так как по этой же теореме искомая хорда абсолюта должна лежать на проективной прямой, проходящей через точки Р и Р', а через две точки проективной плоскости проходит только одна прямая.

Понятие о сферической геометрии

1. Сферическая геометрия изучает свойства фигур, лежащих на сфере евклидова пространства.

Пусть S — некоторая сфера с центром О радиуса r. Возьмем плоскость , удаленную от точки О на расстояние, меньшее r. Тогда пересечение плоскости  и сферы S есть окружность, которую назовем большой окружностью, если О, и малой окружностью, если О.

В геометрии на сфере большие окружности играют роль прямых на плоскости. Здесь есть определенная аналогия: для любых двух точек А, ВS существует большая окружность, проходящая через эти точки. Но есть и отличие: большая окружность единственная только тогда, когда точки А и В не являются диаметрально противоположными. Далее, на плоскости Евклида и на плоскости Лобачевского существуют непересекающиеся прямые, тогда как на сфере любые две различные большие окружности пересекаются в двух точках (диаметрально противоположных).

Известно, что любая большая окружность Q сферы S делит ее на две части, которые называются полусферами, а сама окружность Q — краем этих полусфер. В геометрии на сфере полусфера играет ту же роль, что и полуплоскость в планиметрии.

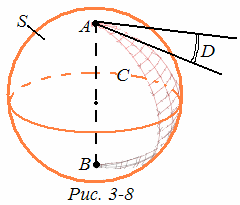
Пусть А и В — две диаметрально противоположные точки сферы S, АСВ и ADB — две какие-либо полуокружности с концами в точках А и В, а фигура Г — объединение этих полуокружностей (рис.3-8).

Можно показать, что фигура Г делит фигуру S\Г на две части D' и D" (на рис. 3-8 одна из этих частей заштрихована). Каждая из фигур D₁=D’Г, D₂=D"Г называется двуугольником с вершинами в точках А и В.

Данные полуокружности АСВ и ADB называются сторонами этих двуугольников. Двуугольник — аналог угла на плоскости: двуугольник является или пересечением, или объединением двух полусфер, края которых не совпадают. Ясно, что двуугольник можно рассматривать как пересечение сферы S с двугранным углом С АВ D. Линейный угол этого двугранного угла называется углом данного двуугольника. Его можно рассматривать как угол между касательными в точке А (или В) к большим окружностям, содержащим стороны двуугольника. Если этот угол прямой, то двуугольник называется прямоугольным.

Пусть Q₁ и Q₂ — две большие окружности. Q₁∩Q₂ ={А,В}. Мы имеем здесь две пары вертикальных двуугольников, высекаемых на сфере S двумя парами вертикальных двугранных углов, полученных при пересечении плоскостей ₁Q₁ и ₂Q₂. Если один из этих двуугольников прямоугольный, то и остальные три прямоугольные. В этом случае большие окружности Q₁ и Q₂ называются перпендикулярными: Q₁Q₂. Ясно, что окружности Q₁ и Q₂ перпендикулярны тогда и только тогда, когда плоскости ₁ и ₂ перпендикулярны.

Если Q — большая окружность, а АВ — диаметр сферы, перпендикулярный к плоскости этой окружности, то точки А и В называются полюсами окружности Q. Если точка M₁ не является полюсом окружности Q, то существует, и притом единственная, большая окружность Q₂, проходящая через точку M₁ и перпендикулярная окружности Q. Чтобы получить эту окружность Q₂, надо пересечь сферу S плоскостью, которая проходит через прямую ОМ₁ перпендикулярно плоскости окружности Q₁. Если же точка M₁ является полюсом большой окружности Q₁, то любая большая окружность, проходящая через точку M₁, перпендикулярна окружности Q₁. В этом снова проявляется отличие сферической геометрии от геометрии на евклидовой плоскости (или на плоскости Лобачевского), где через любую точку плоскости проходит единственная прямая, перпендикулярная к данной прямой.

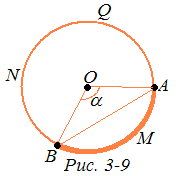
2. Возьмем две точки A,BS и рассмотрим большую окружность Q, проходящую через эти точки (рис. 3-9). Окружность Q является объединением двух своих дуг и с концами в точках А и В. Длина той из этих двух дуг, которая не больше полуокружности, называется сферическим расстоянием между точками А и В и обозначается через d(A,B). Следовательно, для любых двух точек сферы S имеем d(A,B)r.

Пусть меньше полуокружности, и, значит, d(A,B) — длина этой дуги. Обозначим через а величину центрального угла АОВ, опирающегося на дугу АМВ, и через (А,В) – длину отрезка АВ. Как известно,

d(A,B) = r. (1)

Из треугольника АОВ (рис. 3-9) находим:

(2)

Из формул (1), (2) следует:

(3)

3. Движением сферы называется всякое изометрическое отображение этой сферы на себя, т. е. такое отображение f : SS, которое удовлетворяет условию: каковы бы ни были точки А и В сферы, d(A,B) = d(f(A), f(B)). Из формулы (3) следует, что в этом случае (А,В)=(f(А), f(В)). Следовательно, любое движение f сферы S порождается некоторым движением f₀ пространства, причем f₀(О)=О. Обратно: любое движение g₀ пространства, оставляющее точку О инвариантной, порождает определенное движение сферы S.

Отсюда заключаем, что множество всех движений сферы S является группой, которая изоморфна стационарной подгруппе Н₀ точки О в группе движений пространства.

Две фигуры F, F' S называются конгруэнтными или равными, если существует такое движение сферы S, которое переводит одну из этих фигур в другую. Следовательно, фигуры F, F'  S конгруэнтны, если они Н₀ – эквивалентны.

4. Возьмем на сфере S три точки А,В,С, не лежащие на одной большой окружности. Они определяют три полусферы, каждая из которых содержит точки А,В,С, причем две из этих точек принадлежат краю полусферы. Пересечение этих трех полусфер называется сферическим треугольником с вершинами А,В,С. Дуги АВ, ВС, АС больших окружностей (меньшие полуокружности) называются сторонами сферического треугольника ABC.

Пусть ABC — сферический треугольник, а = d(B,C), b = d(A,C), с = d(A,B) — длины его сторон, , ,  соответственно углы ВОС, АОС и АОВ.

Докажем теорему синусов для сферического треугольника.

Теорема. Пусть а=d{B,C), b=d{A,C), с=d{A,B) — стороны сферического треугольника ABC, a r — радиус сферы. Тогда

(4)

доказательство

Можно доказать, что справедливо следующее равенство, которое выражает теорему косинусов для сферического треугольника ABC:

(7).

Можно так же доказать, что площадь сферического треугольника ABC вычисляется по формуле

, (8)

где — так называемый избыток сферического треугольника. Так как площадь S_ABC>0, то из формулы (8) следует,что > 0, т. е. . Итак, сумма углов любого сферического треугольника больше . Это — существенное отличие геометрии на сфере как от геометрии на плоскости Евклида, так и от геометрии на плоскости Лобачевского

Модель Пуанкаре

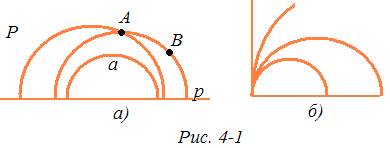
Модель Пуанкаре геометрии Лобачевского. (Французский ученый Анри Пуанкаре (1854—1912) — крупнейший математик. Описываемая далее модель была предложена им в 1882г.) Роль плоскости Лобачевского играет открытая полуплоскость; роль прямых выполняют содержащиеся в ней полуокружности с центрами на ограничивающей ее прямой и лучи, перпендикулярные этой прямой. Роль наложений выполняют композиции инверсий относительно этих полуокружностей и отражений в лучах. Все аксиомы евклидовой геометрии здесь выполняются, кроме аксиомы параллельных (рис. 4-1, а), тем самым в этой модели выполняется геометрия Лобачевского.

Опишем эту модель более подробно и докажем сказанное. Берем на обычной евклидовой плоскости какую-нибудь прямую р и ограниченную ею открытую полуплоскость Р. Прямую р назовем граничной прямой. Полуплоскость Р будет играть роль плоскости Лобачевского; мы будем называть ее «плоскостью» в кавычках. Точками в модели будут точки этой «плоскости», т. е. полуплоскости Р. За «прямые» в модели принимаем, во-первых, содержащиеся в Р полуокружности, центры которых лежат на граничной прямой (рис. 4-1, а). «Отрезок» АВ в модели — это дуга такой полуокружности с концами A, В.

Подчеркнем, что конец «отрезка» не может быть концом полуокружности, представляющей прямую; ее концы исключены вместе с граничной прямой; «плоскость» — это открытая полуплоскость. Точка «прямой» служит общим началом двух «лучей» — двух дуг полуокружности (с исключенными концами). «Углом» назовем фигуру из двух «лучей» с общим началом, не содержащихся в одной «прямой» (рис. 4-1, а).

Помимо указанных «прямых» есть еще «прямые» — это полупрямые, перпендикулярные граничной прямой. Они являются пределами рассмотренных полуокружностей (рис. 4-1,б). Когда центр полуокружности удаляется по граничной прямой, а полуокружность проходит через данную точку, то она «распрямляется» и в пределе переходит в полупрямую. Поэтому мы дальше будем мыслить указанные полупрямые среди «прямых» модели в качестве полуокружностей, как «полуокружности бесконечного радиуса». Это позволит обойтись без скучных оговорок, касающихся этих полупрямых, причем, однако, следует помнить условность этого и быть готовым проверять утверждения для таких «полуокружностей». («Отрезок» на такой «прямой» — это обычный отрезок, а «лучи» — один обычный луч, другой — отрезок с исключенным концом на граничной прямой.)

Рассмотрим теперь в этой модели те аксиомы, в которые не входит понятие о равенстве отрезков и углов.

Аксиома параллельных для прямых относится к таким аксиомам. В данной модели она явно не выполняется: через точку А, не лежащую на «прямой» а, проходит бесконечно много «прямых», не имеющих с а общих точек (рис. 4-1,а).

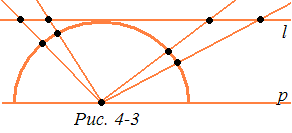
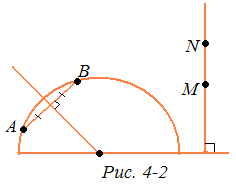
Все прочие аксиомы, говорящие о связи точек и отрезков или точек и прямых, о взаимном расположении точек и прямых, здесь выполняются. Так, на рис. 4-2 указано построение отрезка с данными концами. Далее, возьмем полуокружность, представляющую «прямую» в модели. Проведем прямую l, касающуюся этой полуокружности и параллельную граничной прямой. Спроектируем полуокружность из ее центра на прямую l (рис.4-3). Получим взаимно однозначное, сохраняющее порядок точек, соответствие между точками прямой и полуокружности, т. е. «прямой» модели. Все свойства, выраженные в аксиомах, будут одни и те же. Они также очевидно выполнены на полупрямых, представляющих «прямые» модели. Аксиома деления плоскости также выполняется. «Прямая» — полуокружность — делит плоскость на две области — внутреннюю и внешнюю. Это и будут «полуплоскости» в нашей модели. Из одной в другую нельзя перейти по какой-либо дуге, не пересекая разделяющую их «прямую» — полуокружность.

Остается определить равенство «отрезков» и «углов» так, чтобы выполнялись соответствующие аксиомы. Это мы сделаем, определив «наложение». Сначала определим «отражение в прямой». За «отражение в прямой» примем инверсию в той окружности, полуокружность которой представляет данная «прямая». Если же «прямая» — это полупрямая, перпендикулярная граничной прямой, то «отражением» в ней будет обычное отражение.

«Наложением» в модели называем любую композицию «отражений». «Равными» считаем фигуры, в частности, «отрезки» и «углы», совмещаемые «наложением».

Это определение сразу приводит к выводу: углы, «равные» в модели, равны без кавычек — в обычном смысле. В самом деле, углы при инверсиях сохраняются, т. е. преобразуются в равные, но они «равны» в модели по определению. Обратно: углы, «равные» в модели, — это т.е., которые преобразуются друг в друга «наложениями», т. е. инверсиями, и, стало быть, они равны в обычном смысле.

При инверсии в окружности с центром на граничной прямой эта прямая и полуплоскость Р отображаются на себя. Поэтому содержащаяся в Р полуокружность с центром на граничной прямой отображается на такую же полуокружность. В модели это означает, что при «отражениях» «прямые» переходят в «прямые». Очевидно, что также «лучи» переходят в «лучи» и «отрезки» — в «отрезки».

Обратимся к откладыванию отрезков и углов в модели. Понятия, относящиеся к модели, будем предварять знаком *.

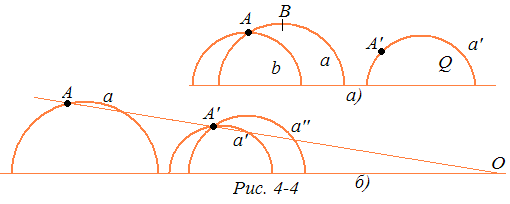
Пусть даны точка А, *луч а с началом А, *отрезок АВ на этом *луче и *угол ab с вершиной А, образованный *лучом а вместе с *лучом b. Пусть даны также точка А', исходящий из нее *луч а', и отмечена * полуплоскость Q, ограниченная *прямой, содержащей *луч а' (рис. 4-4,а). Нам нужно произвести *наложение, переводящее точку А в А’, *луч а — в а' и *луч b — в *луч, лежащий в *полуплоскости Q так, что *угол, *равный ab, отложится от а' в эту *полуплоскость.

Проведем прямую АА', и пусть она пересекает граничную прямую р в точке О (рис. 4-4,б). Произведем инверсию с центром О, которая переведет А в А'. *Луч а перейдет в *луч а" с началом А', он образует с *лучом а' *угол а'а").

Проведем прямую q (без кавычек), делящую *угол а'а" пополам, и построим окружность с центром на граничной прямой, касающуюся прямой q (кстати, укажите такое построение). Инверсия в этой окружности переведет *луч а" в а' (почему?). В смысле модели это значит, что *отражение в соответствующей *прямой переводит *луч а" в а'. Таким образом, два отражения переводят точку А в А' и *луч а — в а'. Вместе с *лучом вся содержащая его *прямая — полуокружность — переходит в *прямую — полуокружность,— содержащую *луч а'. *Полуплоскости, ограниченные *прямой , отображаются на *полуплоскости, ограниченные *прямой . *Луч b, служащий стороной данного *угла ab, переходит в *луч b" с началом А'. Но он может оказаться не в той *полуплоскости, которая была заранее отмечена. Тогда нужно произвести еще *отражение в *прямой, содержащей *луч а', т. е. инверсию в окружности, содержащей эту *прямую. При этом на самой *прямой ничего не происходит: все ее точки остаются неподвижными. И только *луч b" перейдет в *луч b, лежащий в указанной *полуплоскости.

Если на *луче а была отмечена какая-нибудь точка В, и тем самым отмечен *отрезок АВ, то эта точка перейдет в определенную точку В' на *луче а' и *отрезок АВ — в *отрезок А'В' на этом * луче. Так мы получаем результат: на каждом *луче а' можно от его начала отложить *отрезок, *равный данному, т. е. для любого данного *отрезка АВ на данном *луче с началом А' есть такая точка В', что *отрезок АВ можно перевести в *отрезок А'В' путем *наложения.

Совершенно так же то, что *луч b перейдет в *луч b', лежащий в нужной полуплоскости, что и *угол а'b' равен данному ab, позволяет утверждать:

От каждого *луча от его начала по данную сторону от *прямой, его содержащей, можно отложить *угол, равный данному.

Остается доказать, что *угол откладывается единственным образом, так же, как и *отрезок (или, по нашей аксиоме меньшего отрезка, отрезок, содержащийся в данном и не совпадающий с ним, не может быть равен ему).

Утверждение о единственности откладывания угла сводится, очевидно, к следующему:

Если *лучи b, с, исходящие из начала *луча а, образуют с ним равные углы и лежат с одной стороны от него (в одной полуплоскости), то они совпадают.

Но *углы, равные в модели, равны в обычном «евклидовом» смысле, а для обычных углов сказанное, очевидно, верно. *Лучи b, с содержатся в окружностях с центрами на данной прямой р. Раз они образуют с *лучом а данный угол, то, значит, дана касательная к указанным окружностям в точке А. Но окружность с центром на данной прямой, касающаяся другой прямой в данной ее точке, только одна. Значит, *лучи b, с совпадают. Итак, *угол откладывается единственным образом.

*Отрезок, *равный данному, также откладывается на данном *луче единственным образом. Действительно, пусть *отрезок АВ, *равный данному, отложен на данном *луче а с началом А. Если бы можно было отложить другой *отрезок, АС, равный тому же, то это значило бы, что есть *наложение (отличное от тождественного), отображающее *луч сам на себя. Оно отображает тогда на себя и всю содержащую его *прямую — полуокружность а. Если же *наложение переставляет *полуплоскости, ограниченные *прямой а, то добавив отражение в ней, можно добиться того, что и полуплоскости эти будут отображаться каждая на себя.

В таком случае, ввиду сохранения углов, все *лучи, исходящие из точки А, будут отображаться на себя. Значит, при такой композиции инверсий (и отражений в вертикальных лучах) все концы лучей на граничной прямой остаются на месте. Вместе с ними отображаются на себя все полуокружности с концами на граничной прямой, т. е. *прямые модели. Но каждую точку можно получить в пересечении этих *прямых. Поэтому все точки отображаются на себя — «остаются на месте» — так что рассматриваемое *наложение оказывается тождественным вопреки предположению.

Этим единственность откладывания на данном луче отрезка, равного данному, доказана.

На этом доказательство того, что в рассмотренной модели выполняется геометрия Лобачевского, заканчивается. Требование аксиомы меньшего отрезка, что в отрезок нельзя уместить ему равный, заведомо. Выполняется при том, что уже доказано. Впрочем, доказательство того, что оно выполнено, читатель может провести сам.

Описанную модель плоскости Лобачевского можно еще назвать конформной, поскольку в ней наложения представляются инверсиями — преобразованиями, сохраняющими углы.

Модель геометрии Лобачевского в пространстве

Эта модель определяется аналогично модели на плоскости. За пространство принимается открытое полупространство Р. «Плоскостями»» в нем служат содержащиеся в Р полусферы с центрами на граничной плоскости, а также перпендикулярные ей открытые полуплоскости. За «прямые»» принимаются полуокружности, перпендикулярные граничной плоскости (т. е. касательные к ним в концах перпендикуляры этой плоскости; центры их лежат на граничной плоскости), а также перпендикулярные ей лучи. Роль «наложений»» играют композиции инверсий в сферах с центрами на граничной плоскости и отражений в перпендикулярных ей плоскостях.

Модель геометрии Лобачевского на поверхности

Оказывается, что геометрия Лобачевского реализуется на поверхностях постоянной отрицательной кривизной: внутренняя геометрия такой поверхности и есть геометрия Лобачевского. Только не на всей плоскости, а на той ее части, которая может быть представлена данной поверхностью. Вместе с тем доказано, что не существует (в трехмерном евклидовом пространстве) никакой поверхности, которая своей внутренней геометрией представляла бы всю плоскость Лобачевского.

Во внутренней геометрии поверхности роль прямолинейных отрезков играют кратчайшие линии (отрезки геодезических); роль наложений — такие отображения фигур, содержащихся в поверхности, которые сохраняют расстояния, измеряемые по этим кратчайшим линиям.

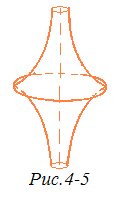
Самая известная из поверхностей постоянной отрицательной кривизны — псевдосфера — изображена на рис. 4-5.

Реализацию геометрии Лобачевского на поверхностях постоянной отрицательной кривизны установил итальянский математик Бельтрами (в 1861 г.).

Впрочем, еще за 30 лет до него это установил, собственно, Миндинг — профессор университета в Дерпте (ныне Тарту), — но не понял этого.

Доказательство логической непротиворечивости геометрии Лобачевского

Мы докажем непротиворечивость системы аксиом планиметрии Лобачевского, состоящей из четырех групп I_1-3, II_1-4, III_1-5, IV_1-2 аксиом Гильберта (аксиомы абсолютной планиметрии) и аксиомы V* Лобачевского. При решении этой задачи предполагается, что евклидова геометрия (т. е. система аксиом ∑_H Гильберта) непротиворечива. Мы построим из объектов евклидовой плоскости модель плоскости Лобачевского, которая называется евклидовой моделью Кэли — Клейна. Рассмотрим на евклидовой плоскости некоторую окружность ω с центром О радиуса r = 1 и назовем ее абсолютом. Обозначим через Ω круг с границей ω, а через множество внутренних точек этого круга.

Введем следующие соглашения. Неевклидовой точкой назовем любую евклидову точку М, а неевклидовой прямой — любую хорду (без концов) окружности ω. Отношения «принадлежность» и «лежать между» понимаем в обычном смысле. Неевклидовы прямые будем обозначать так: UV, U₁V₁ и т. д., предполагая, что U, V, U₁, V₁ . Таким образом, неевклидовыми точками прямой UV будут те и только те евклидовы точки, которые лежат между точками U и V.

Нетрудно убедиться в том, что при этих соглашениях выполняются все аксиомы I_1-3, II_1-4 Гильберта. Проверим в качестве примера аксиому. Пусть А и В — две неевклидовы точки, a UV — неевклидова прямая, на которой они лежат. Так как А и В — внутренние точки хорды UV, то на этой хорде существует хотя бы одна внутренняя точка С, такая, что А — В — С. Отсюда мы заключаем, что существует по крайней мере одна неевклидова точка С, такая, что неевклидова точка В лежит между неевклидовыми точками А и С.

Так как в построенной модели выполняются все аксиомы групп I, II Гильберта, то выполняются и все следствия из этих аксиом, в частности имеют место теоремы, с помощью которых вводятся понятия луча и полуплоскости. Ясно, что неевклидовым лучом, исходящим из точки С, является множество всех внутренних точек произвольной полухорды CU окружности ω (CU — евклидов отрезок, где С — внутренняя точка круга Ω, a U — точка на его границе). Неевклидовой полуплоскостью является множество всех внутренних точек какого-нибудь сегмента круга Ω.

Для того чтобы в нашей модели определить равенство отрезков и углов, введем ряд вспомогательных понятий. Напомним, что на евклидовой плоскости простым отношением трех точек А, В и С, лежащих на одной прямой, называется число (АВ, С) = λ, такое, что , а сложным отношением четырех точек А, В, С, D, лежащих на одной прямой,— число (АВ, CD) = . Из этого определения непосредственно вытекают следующие свойства.

1. Если (АВ, CD) = (АВ, CD'), то точки D и D' совпадают.

2. Для любых четырех точек А, В, С, D прямой имеем (АВ, CD) = (CD, AB)= = (ВА, DC) = (DC, BA).

Если четыре точки на прямой заданы своими координатами M₁(x₁, у₁), М₂ (х₂, y₂), М₃ (х₃, у₃) и M₄ (х₄, у₄), то

. (1)

Одна из этих формул теряет смысл, если данные точки лежат на прямой, параллельной одной из координатных осей.

Биективное отображение f : Ω → Ω назовем -преобразованием, если выполнены следующие условия.

а) Внутренние точки круга Ω переходят во внутренние точки этого же круга, а граничные точки этого круга — в граничные точки.

б) Любая хорда окружности ω переходит в некоторую хорду этой же окружности, и при этом сохраняется сложное отношение соответственных точек.

Рассмотрим примеры -преобразований.

Пример 1. Любое движение евклидовой плоскости, имеющее центр абсолюта своей инвариантной точкой, индуцирует во множестве Ω некоторое -преобразование. В частности, тождественное преобразование множества Ω, вращение вокруг центра О круга Ω, отражение от любого диаметра круга Ω являются примерами -преобразований.

Пример 2. Пусть отображение f : Ω → Ω в системе координат Оху задано формулами

, ,где |a| < 1 (2)

Так как для точек множества Ω: — 1 ≤ х ≤ 1, то 1 — ах ≠ 0, поэтому каждая точка множества Ω имеет образ. Из формул (2) получаем:

(3)

,. (4)

Из равенства (3) следует, что точки абсолюта ω при отображении f переходят в точки абсолюта, а точки множества — в точки того же множества . Далее, из равенств (4) мы заключаем, что каждая точка (х', у') множества Ω имеет единственный прообраз (х, у), поэтому отображение (3) является биекцией множества Ω.

Отметим, что преобразование f, как показывают формулы (2) и (4), является инволютивным, т. е. f ^-1 = f.

Докажем, что для преобразования f выполняются также условия б). Если точки M₁, M₂,, M₃ лежат на прямой Ах + By + С = 0, то, используя формулы (4), мы убеждаемся в том, что их образы M’₁, M’₂,, M’₃ также лежат на некоторой прямой. Таким образом, если UV — некоторая хорда окружности ω, а U = f(U), V = f(V), то все точки хорды UV переходят в точки хорды U'V’. Но так как f ^-1 = f, то все точки хорды U'V’ переходят в точки хорды UV. Таким образом, хорда UV переходит в хорду U'V’.

Остается доказать, что преобразование (2) сохраняет сложное отношение четырех точек. Пусть M₁(x₁, у₁), М₂ (х₂, y₂), М₃ (х₃, у₃), M₄ (х₄, у₄)— четыре точки, лежащие на одной прямой, пересекающей ось Оу, а М'_i(х_i, у_i), i= 1, 2, 3, 4,— их образы. Используя первую из формул (4), находим:

где i , j = 1, 2, 3, 4, i ≠ j.

Отсюда, применяя формулу (1), получаем (М₁М₂, М₃М₄) = (М’₁M’₂, М'₃M’₄). Если точки М_i лежат на прямой, параллельной оси Оу. или на оси Оу, то используя вторую из формул (4), приходим к тому же выводу. Итак, доказано, что формулами (2) задано инволютивное -преобразование.

Рассмотрим некоторые свойства -преобразований. Из определения -преобразования непосредственно следует утверждение.

1°. Если f и g — -преобразования, то fg и f ^-1 являются -преобразованиями.

2°. Любое -преобразование сохраняет отношение «лежать между» точек круга Ω.

□ Пусгь А, В, С и А — В — С, а А', В', С' — образы этих точек. Обозначим через UV хорду, на которой лежат данные точки, а через U'V' образ этой хорды. Если точки А и С являются концами хорды UV (т. е. сов- падают с тачками U и V), то А' и С' являются концами хорды U'V'. В этом случае утверждение 2° очевидно. Предположим, что тачка U не совпадает ни с одной из точек А и С. Тогда (АС, ВU) = (А'С', B'U') или . Так как (АС, V) < 0, (А'С', V') < 0 и по условию (АС, В) > 0, то из последнего равенства следует, что (А'С', В') > 0. Это означает, что А' — В' — С.

Отсюда мы заключаем, что при -преобразовании отрезок, принадлежащий кругу Ω, переходит в отрезок; в частности, полухорда круга Ω переходит в полухорду того же круга. Далее, любой сегмент круга Ω переходит в сегмент того же круга.

Пусть UV - хорда круга Ω. AU — полухорда этой хорды, а — одни из сегментов, ограниченный хордой UV. Пару AU, назовем -флагом и обозначим через (AU, ). На рисунке 1 изображены два -флага (A₁U₁, ) и (A₂U₂ , ). Из предыдущего ясно, что -преобразование любой -флаг переводит в -флаг.

3. Какова бы ни была внутренняя точка А круга Ω. существует инволютивное -преобразование, которое переводит точку А в центр О круга Ω, а точку О в точку А.

□ В самом деле, пусть ОА = а. Выберем прямоугольную систему координат Оху так, чтобы точка А в этой системе имела координаты А(а, 0). Тогда -преобразование, заданное формулами (2), переводит точку А в точку О, а точку О в точку А.

4. Каковы бы ни были флаги I₁ = (A₁U₁, ) и I₂ = (A₂U₂, ), существует -преобразование, которое I₁ переводит в I₂ (рис. 1).

□ По свойству 3° существуют инволютивные -преобразования f₁ и f₂, такие, что О = f₁(A₁) и О = f₂(А₂), где О - центр круга Ω. Пусть I₁' = f₁(I₁) и I₂' = f₂(I₂). Рассмотрим -преобразование f₀, такое, что I₂' = f₀(I₁') (f₀ является вращением вокруг точки О или вращением вокруг точки О с последующим отражением от диаметра круга Ω). Тогда f = f₂f₀f₁ является искомым -преобразованием, так как f(I₁) = f₂f₀f₁(I₁) = f₂f₀(I₁ ') = f₂(I₂ ') = I₂.

Отсюда получаем утверждение.

5°. Каковы бы ни были полухорды A₁U₁ и A₂U₂, существует -преобразование, которое полухорду A₁U₁ переводит в полухорду A₂U₂.

6°. Если -преобразование какой-нибудь -флаг переводит в себя, то оно является тождественным преобразованием круга Ω.

В этом пункте для простоты изложения неевклидовы отрезки, лучи, углы, полуплоскости будем называть просто отрезками, лучами, углами, полуплоскостями. Введем следующие соглашения. Будем считать, что отрезок АВ ранен отрезку А'В', если существует такое -преобразование, которое отрезок АВ переводит в отрезок А'В'. Аналогично угол hk считается равным углу h'k', если существует -преобразование f, которое угол hk переводит в угол h'k' (т. е. h' = f(h) и k' = f(k) или k' = f(h) и h' = f(k)).

Заметим, что если hk = h'k', то всегда найдется такое -преобразование f', что h' = f'(h), k' = f'(k). В самом деле, допустим, что равенство hk = h'k' означает существование такого -преобразования, что k' = f(h), h' = f(k). Рассмотрим инволютивное -преобразование f₁, которое вершину угла hk переводит в центр О круга Ω. (свойство 3°). Пусть h₁ = f₁(h), k₁ = f₁(k). Если f₂ - симметрия с осью, содержащей биссектрису угла h₁k₁, то k₁ = f₂(h₁), h₁ = f₂(k₁). Поэтому f' = ff₁f₂f₁ является искомым -преобразованием.

Покажем, что все аксиомы группы III Гильберта выполнены.

Ш₁. Пусть АВ — данный отрезок, отложенный на луче h, a h' —луч, исходящий из точки А'. Докажем, что существует точка B' h', такая, что А'В' = АВ.

Обозначим через AU и A'U' полухорды крута Ω, на которых лежат лучи h и h', а через UV и U'V' соответствующие хорды. Рассмотрим -преобразование f, которое полухорду AU переводит в полухорду A'U' (свойство 5°). Тогда h' = f(h). Если В' = f(B), то В' h', и по определению А'В' = АВ.

Замечание. В нашей модели на луче h' существует единственная точка В', удовлетворяющая условию АВ = А'В'. В самом деле, U' = f(U), V' = f(V), поэтому (UV, АВ) = (U'V', А'В'). Если допустить, что на луче h' существует другая точка В", такая, что АВ = А'В", то аналогично получаем (UV, АВ) = (U'V', А'В"). Поэтому (U'V', А'В') = (U'V', А'В"). По свойству 1° сложного отношения четырех точек точки В' и В" совпадают.

III₂. Выполнение этой аксиомы непосредственно следует нз свойства 1° -преобразований.

III₃. Пусть А — В — С, А' — В' — С', АВ = А'В' и ВС = В'С'. Докажем, что АС = А'С'. Рассмотрим полухорды BU₁, BU₂, B'U'₁, B'U'₂, на которых лежат соответственно точки А, С, А' и С' (рис. 2). По свойству 5° существует такое - преобразование f, которое полухорду BU₁ переводит в полухорду B'U'₁. При этом полухорда BU₂ переходит в полухорду B'U'₂. Пусть А₁ = f(А), С₁ = f(С).

Так как ВА = В'А' по условию и ВА = В'А₁ по построению, то точки А' и А₁ совпадают, т. е. А' = f(A) (см. замечание к аксиоме III₁). Аналогично доказывается, что точки С и С₁ совпадают, поэтому С' = f(C). Таким образом, -преобразование f отрезок АС переводит в отрезок А'С', т. е. АС = А'С'.

III₄. Пусть даны угол hk и флаг (A', h', λ'). Докажем, что существует единственный луч k' λ' такой, что hk = h'k'. Для этого рассмотрим -флаги I = (AU, ) и I' = (A'U', '), которые выбраны так, что h AU, h' A'U', k , λ' '. По свойству 4° существует такое -преобразование f, что I' = f(I). Луч k' = f(k) является искомым, так как k'λ' , и по определению равенства углов hk = h'k'.

Предположим, что k" — луч, удовлетворяющий условиям: hk = =h'k'' и k" I'. Тогда, очевидно, h'k' = h'k", поэтому существует такое -преобразование f, что h' = f(h'). k" = f(k'). Отсюда мы заключаем, что преобразование f -флаг I' переводит в себя. По свойству 6° f — тождественное преобразование круга Ω, следовательно, лучи h' и k" совпадают.

Ш₅. Пусть в треугольниках ABC и А'В'С имеем АВ = А'В', АС = А'С' и ВАС = В'А'С'. Докажем, что ABC = А'В'С'.

Так как ВАС = В'А'С', то существует такое -преобразование f, которое переводит луч АВ в луч А'В', а луч АС в луч А'С'. Пусть В₁ = f(B) и С₁ = f(C). Так как A' = f'(А), то АВ = А'В₁. Но по условию АВ = А'В'. поэтому точки В₁ и В' совпадают, т. е. В' = f(B) (см. замечание к аксиоме III₁). Аналогично доказывается, что С' = f(С). Таким образом, -преобразование f точки А, В, С переводит соответственно в точки А', В', С', поэтому ABC = =А'В'С.

IV₁ и IV₂. Группа IV аксиом Гильберта эквивалентна предложению Дедекинда. Ясно, что предложение Дедекинда выполняется на построенной нами модели, поэтому выполняются аксиомы IV₁ и IV₂ Гильберта.

V*. Возьмем произвольную прямую UV и точку А, не лежащую на ней. Рассмотрим прямые UU₁ и VV₁, проходящие через точку А (рис. 3). Эти прямые не пересекаются с прямой UV, так как евклидовы точки U и V не являются неевклидовыми точками прямой UV. Таким образом, имеет место аксиома V* Лобачевского.

Таким образом, построив евклидову модель Кэли — Клейна, мы тем самым доказали, что система аксиом I_1-3, II_1-4, III_1-5, IV_1-2, V* непротиворечива, если непротиворечива система аксиом ∑_Н Гильберта.

Вывод: V постулат Евклида не зависит от остальных аксиом евклидовой планиметрии.

Литература

Основная

1. Александров А.Д. Основания геометрии: Учебное пособие для вузов. М..; Наука, 1987 г.

2. Атанасян Л..С, Базылев В.Г. Геометрия, ч П. М.; 1989 г.

3. Базылев В.Т., Дуничев К.И.. Геометрия, ч П. М.; 1975 г.

4. Сборник задач по геометрии под редакцией В.Т. Базылева, М.; 1980 г.

5. Сборник задач по геометрии под редакцией Л.С. Атанасяна, ч П. М.; 1978г.

Дополнительная

1. Гильберт Д. Основания геометрии. М.; Гостехиздат, 1948 г.

2. Каган В.Ф. Основания геометрии, ч I.M.; Л.; Гостехиздат, 1949 г

3. Костин В.И. Основания геометрии. М.; Л.; Учпедиздат, 1946 г.

4. Погорелов А.В. Основания геометрии. М.; Наука, 1968 г.