Индексы
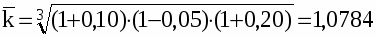
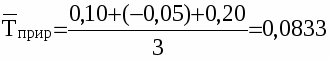
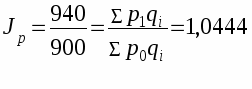
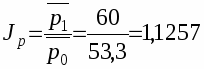
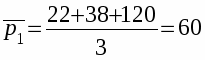

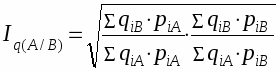
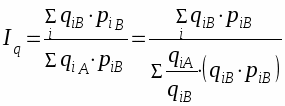
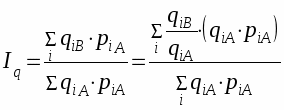
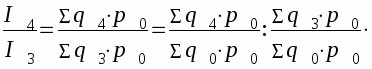
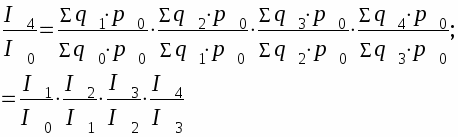
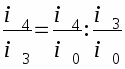
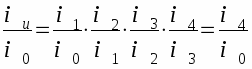
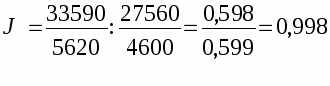
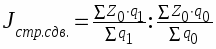
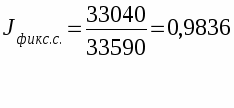
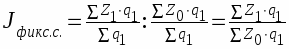
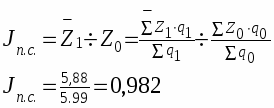
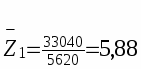
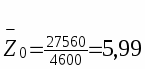
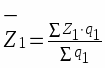
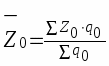
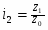
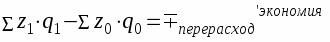
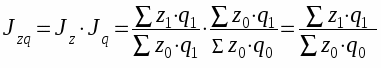
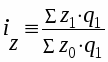
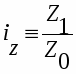
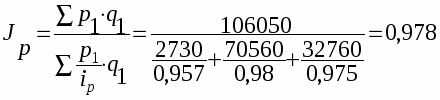
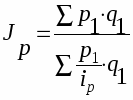
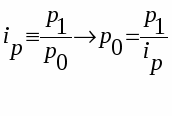
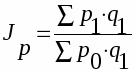
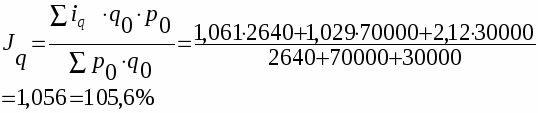
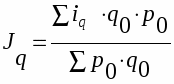
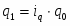
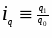
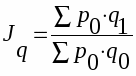
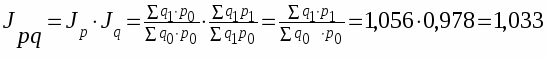
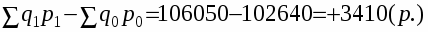
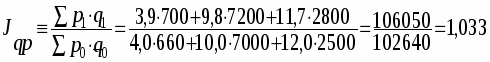
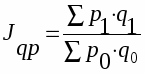
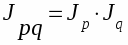
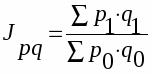
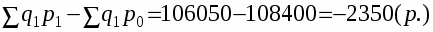
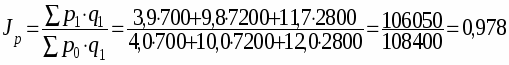
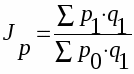
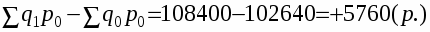
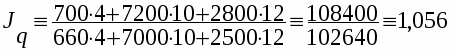
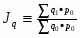
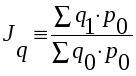


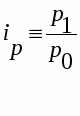
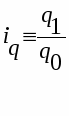
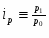
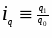
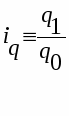
 Содержание
Содержание
1. Понятие об индексах и их роль в экономических исследованиях
2. Классификация экономических индексов
3. Индексы переменного и постоянного состава
4. Ценные и базисные индексы
5. Использование индексов в макроэкономических исследованиях
1. Понятие об индексах и их роль в экономических исследованиях
Метод экономических индексов является одним из важнейших орудий экономико-статистического исследования. В практике индексы наряду со средними величинами являются наиболее распространенными статистическими показателями. С их помощью изучается развитие народного хозяйства в целом и его отдельных отраслей, анализируются результаты производственной деятельности предприятий и объединений, исследуется роль отдельных факторов в формировании важнейших экономических показателей, выявляются резервы производства. Индексы используются в международных сопоставлениях экономических показателей.
Слово индекс (index) в переводе с латинского означает указатель, показатель и имеет различные значения.
Во-первых, под индексом часто понимается всякий числовой показатель, заменяющий собой подробное наименование: номер, рабочий номер официального документа, инвентарный номер станка и т.д.
Во-вторых, под индексом понимается любой относительный показатель изменения социально-экономических явлений во времени: ФЗП, числа рабочих и т.д.
В-третьих, это сводный или общий показатель изменения социально-экономических явлений, состоящих из несводимых непосредственно частей - индекс объема различной продукции.
Что же представляет собой экономический индекс?
Под индексом в статистике понимают относительную величину, получаемую в результате сопоставления социально-экономических явлений во времени, в пространстве или с планом, нормой, стандартом.
Индексный метод широко применяется для характеристики степени выполнения плана, изучения динамики, сравнения уровней экономических явлений в пространстве (в разных странах, республиках и т.д.).
Таким образом, с помощью индексных показателей решаются следующие основные задачи:
характеристика общего сложного изменения экономического явления (изменение затрат на производство продукции, стоимости произведенной продукции);
выделение в показателе изменения сложного явления, влияния одного из факторов (например, увеличение затрат на производство продукции, связанное с ростом выпуска продукции в натуральном выражении).
В качестве самостоятельной задачи можно выделить задачу обособления влияния изменения структуры явления на изменение индексируемой величины (например, при изучении динамики среднеотраслевой себестоимости продукции).
2. Классификация экономических индексов
Способы построения индексов зависят от содержания изучаемых явлений, методологии расчета исходных данных и целей исследования. Для удобства в теории статистики разработана определенная символика. Каждая величина, изменение которой нас интересует (индексируемая величина), имеет свое символическое обозначение.
Например,
количество данного вида продукции обозначается - q;
цена единицы изделия - p;
себестоимость единицы изделия - Z;
трудоемкость единицы изделия - t, и т.д.
По своим аналитическим возможностям индексы являются очень гибким статистическим инструментом; с их помощью возможно многгранное изучение явления.
Все виды индексов можно классифицировать по нескольким группировочным признакам:
I - по степени охвата элементов совокупности:
Различают - индивидуальные (i)
сводные (общие) (J)
II - по базе сравнения:
индексы динамики (базисные, ценные);
индексы выполнения плана;
индексы территориальные;
III - по виду весов:
индексы с постоянными весами или коэффициентами;
индексы с переменными весами или коэффициентами;
IV - по форме построения:
агрегатные;
средние (ср. арифметическая, ср. гармоническая);
V - по составу явления:
индексы постоянного состава;
индексы переменного состава;
VI - по содержанию индексируемых величин:
объемы показателей;
качественных.
Подробнее рассмотрим некоторые виды индексов.
Индексы индивидуальные и общие.
Агрегатный индекс
Индивидуальные - характеризуют изменение только одного элемента совокупности (количество потребляемой электроэнергии, цен и т.д.)
Индивидуальные индексы являются обычной относительной величиной. Так, например, индивидуальный индекс динамики - это отношение отчетного уровня индексируемого показателя к базисному уровню, т.е. это темп роста.
Индивидуальные индексы обозначаются буквой i и сопровождаются подстрочным обозначением индексируемого показателя. Например, индекс продукции в натуральном выражении:
,
где q1, q0 - количество продукции в натуральном выражении в отчетном и базисном периодах.
Общие (сводные) индексы показывают соотношение совокупности явлений, состоящих из разнородных, непосредственно несоизмеримых элементов.
Только в этом случае становится возможным сравнение, следовательно и исчисление индексов.
В общих индексах различают индексируемые величины и веса. Тот показатель, изменение которого характеризует индекс, называется индексируемой величиной. Показатель, применяемый в качестве постоянного, называется весом (соизмерителем).
Агрегатный индекс – основная форма общих индексов.
Основной формой общих индексов является агрегатная форма.
Агрегатным индексом называется соотношение сумм показателей, отражающих порядок расчета общих индексов непосредственно по данным об индексируемых величинах и их весах.
Для математического оформления методики исчисления сводных индексов существует общепринятая система индексной символики. Общие индексы обозначаются символом J. Общий индекс отражает изменение по всей совокупности элементов сложного явления. Если индексы охватывают не все элементы сложного явления, а лишь часть, то их называют групповыми, или субиндексами (например, индексы продукции по отдельным отраслям промышленности).
Рассмотрим на следующем примере построение общих индексов физического объема продукции, цен и стоимости.
Вид про-дук-ции
Един-ица изме-рения
Базисный период
Отчетный период
Индивидуальные индексы продукции
Индивидуальные индексы цен
кол-во
цена за единицу
кол-во
цена за единицу
q0
p1
q1
p1
А
Б
В
кг
шт
шт
660
7000
2500
4,0
10,0
12,0
700
7200
2800
3,9
9,8
11,7
1,061
1,029
1,12
0,975
0,98
0,975
Индивидуальные индексы продукции вычисляются по формуле
,
индивидуальные индексы цен –
.
Общий индекс объема продукции или индекс физического объема продукции (агрегатный):
,
где q - индексируемая величина;
p - соизмеритель.
Для нашего примера
;
или 105,6%, объем продукции в отчетном периоде увеличился на 5,6%
Разность между числителем и знаменателем агрегатных индексов характеризует вы абсолютном выражении изменение сложного показателя за счет изменения индексируемой величины:
Общий индекс цен (агрегатный):
В этом индексе индексируемой величиной является цена, а весом - продукция.
Для нашего примера:
или 97,8%, т.е. цены на всю продукцию снизились на 2,2%.
Разность между числителем и знаменателем - абсолютная фактическая экономия от снижения цен:
Общий индекс т/о продукции:
;
Одним из важнейших общих индексов является общий индекс стоимости продукции и себестоимости продукции:
Этот индекс показывает изменение как объема продукции, так и цен.
Для нашего примера:
или 103,3% т.е. стоимость увеличилась на 3,3% или на 3410 руб.
Между индексами физического объема продукции цен и стоимости существует следующая связь:
Другой формой общих индексов является форма средней величины из индивидуальных индексов. Она связана с преобразованием агрегатного индекса в средний арифметический и средний гармонический индексы.
К таким расчетам прибегают тогда, когда исходные данные не позволяют производить вычисления по агрегатному индексу.
Для получения среднего арифметического индекса необходимо в числителе агрегатной формы индекса индексируемую величину заменять ее значением из индивидуального индекса.
Из формулы индивидуального индекса , , отсюда
Рассчитаем средний арифметический индекс по следующим данным.
Вид продукции
Стоимость продукции в базисном периоде, q0p0,
Индивидуальные индексы продукции, iq
А
Б
В
2640
70000
30000
1,061
1,029
1,120
ИТОГО
102640
Для получения среднего гармонического индекса необходимо в знаменателе агрегатного индекса индексируемую величину заменить ее значением из индивидуального индекса.
Рассмотрим это преобразование на примере индекса цен:
, тогда
Рассчитаем средний гармонический индекс по следующим данным
Наименование продукции
Стоимость продукции в отчетном периоде q1p1
Индивидуальные индексы цен ip
А
Б
В
2730
70560
32760
0,975
0,98
0,975
ИТОГО
106050
т.е. цена снизилась на 2,2%.
Поскольку средние индексы тождественные агрегатным, то по ним вычитая из числителя знаменатель, можно исчислить абсолютные разности.
Индивидуальный индекс себестоимости
характеризует изменение уровня себестоимости единицы какого-либо вида продукции в отчетном году по сравнению с базисным.
Для определения общего изменения уровня себестоимости продукции разных видов используют агрегатный индекс:
Индекс себестоимости и физического объема связана следующим образом:
Jzq - индекс затрат на производство.
3. Индексы переменного и постоянного состава
Наряду с определением изменения уровня себестоимости единицы продукции на отдельном предприятии перед статистикой обычной ставиться задача охарактеризовать изменение себестоимости единицы отдельного вида продукции по всем предприятиям, изготовляющим данный вид продукции.
Например, необходимо установить среднюю себестоимость и влияние на нее по двум ТЭЦ.
№
ТЭЦ
Базисный период
Отчетный период
Затраты на производство э/э, т. р
Индивидуальный индексы себестоимости
Выработано э/э
млн. кВтч
q0
Себе-стоимость
1 кВтч
Z0
q1
Z1
Базисный период
Z0, q0
Отчетный период
Z1, q1
1
2
3
4
5
6
7
8
1
4000
5,9
5000
5,8
23600
29000
0,983
2
600
6,6
620
6,52
3960
4040
0,988
Итого
4600
5,99
5620
5,88
27560
33040
Уровень себестоимости на отдельной ТЭЦ в отчетном периоде снизился соответственно на 1,7 1,2% (графа 8).
Для оценки снижения уровня себестоимости 1 кВтч по двум ТЭЦ рассчитаем средние уровни себестоимости.
В базисном периоде
В отчетном периоде
Зная среднюю себестоимость единицы продукции в отчетном периоде можно определить ее изменение при помощи индекса переменного состава:
т.е. средняя себестоимость снизилась на 1,8%
Изменение средней себестоимости 1 кВтч электроэнергии за счет изменения уровня себестоимости на каждой станции оценивается индексом себестоимости фиксированного состава. Для этого среднюю себестоимость продукции в базисном периоде корректируют на структуре фактически выпущенной продукции:
т.е. в среднем уровни с/с по отдельным станциям снизились на 1,64%.
Для установления влияния объемов производства на с/с 1 квт. ч используется индекс структурных сдвигов.
Следует, за счет изменения в соотношении выпуска эл. энергии между станциями себестоимость снизилась на 0,2%.
4. Ценные и базисные индексы
В ходе экономического анализа очень часто явление изучается за ряд последовательных периодов. В таком случае могут быть вычислены два вида индексов ценный и базисный.
Ценные характеризуют уровни в отдельных периодах в сравнении с уровнями в соседних периодах.
Базисные - характеризуют уровни во всех периодах в сравнении с уровнем одного из них.
Для индивидуальных индексов цен, физ. объема и индексов стоимости продукции справедливо следующее правило:
произведение промежуточных по периодам ценных индексов дает базисный индекс последнего периода, т.е.
отношение базисного индекса отчетного периода к базисному индексу предшествующего периода дает цепной индекс отчетного периода:
Эти правила можно применять и в отношении общих индексов при условии постоянного соизмерения, т.е.
1)
2)
Сформулированные правила взаимосвязи в полном объеме применимо к агрегатным индексам стоимости.
Учитывая требованием увязки индексов в систему, можно также сформулировать общее правило в отношении выбора периода к которому относится соизмеритель (вес). При построении агрегатных индексов качественных показателей количественные показатели принимаются на уровне отчетного периода; при построении индексов количественных показателей - качественные показатели принимаются на уровне базисного периода.
5. Использование индексов в макроэкономических исследованиях
Важным направлением статистических исследований является сопоставление макроэкономических показателей различных стран. Проблемы, возникающие при международных сопоставлениях, обусловлены тем, что сравниваемые объекты могут иметь свою структуру показателей и свою систему соизмерителей.
Так, при сопоставлении уровней промышленного производства двух стран А и В могут быть рассчитаны два индекса физического объема: один - с использованием соизмерителей страны А, второй - соизмерителей страны В. Два названных индекса физического объема будут выглядеть следующим образом:
при структуре цен страны А
при структуре цен страны В
где qiA qiB - количество i-го продукта соответственно в стране А и В;
piA и piB - цена i-го продукта в стране А и стране В.
Таким образом будут получены два результата как правило заметно отличающиеся друг от друга. Поэтому для получения единого вывода предлагается в качестве возможного варианта использовать среднюю геометрическую из двух территориальных индексов объема (т.е. можно использовать формулу индекса Фишера)
Традиционным направлением использования индексного метода в статистике развитых стран является анализ состояния рынка ценных бумаг (акций, облигаций).
По степени обобщения исследуемой информации можно выделить следующие показатели рынка ценных бумаг:
интегральные - характеризующие состояние исследуемого рынка в целом одним обобщенным показателем (например, сводный индекс Доу-Джонса "Индекс 65" рассчитывается по акциям 30 крупнейших промышленных корпораций, 20 транспортных и 15 коммунальных);
частные - характеризуют отдельные составные части исследуемого рынка.
Индексы могут рассчитываться ежедневно, еженедельно, ежемесячно, полугодично. Изменения значений индексов рассматривается ака показатель спроса на рынке.
Индекс рынка ценных бумаг может использоваться для различных сопоставлений:
изменение цен определенных акций можно сравнить с индексом определенного сегмента рынка или с индексом всего рынка и прогнозировать будущее движение цен на акции;
можно сопоставить изменение цен в различных сегментах рынка и делать выводы о том, какой сектор из них является наиболее прибыльным для инвесторов;
для сравнения в аналогичных целях цен на акции в различных странах;
для сравнения изменения цен акций мелких и крупных компаний.
На практике используют четыре методических приема для построения интегральных индексов:
рассчитывается темп роста (снижения) средней цены акции, определенной по формуле простой средней арифметической;
рассчитывается темп роста (снижения) средней цены акции (в качестве веса наиболее часто используется количество обращающихся акций);
рассчитывается среднеарифметический темп прироста (снижения) цены акций;
рассчитывается средний геометрический темп прироста (снижения) цены акций.
Рассмотрим эти приемы на примере, показывающем расчет индексов цен акций трех компаний:
Наименование компаний
Курс акций, доля
Кол-во выпущен-ных акций,
млн. ед.,
qi
Прирост курса акций,
%
Рыночная стоимость всех акций, млн. дол.
Базисный период, р0
Текущий период, р1
Базисный
р0*qi
Текущий
р1*qi
Центр
20
22
20
+10
400
440
Омега
40
38
10
-5
400
380
Плюс
100
120
1
+20
100
120
Итого
900
940
Если воспользоваться первым методом расчета индекса цен на акции, то получим следующий результат:
Среднеарифметическая простая цена акций в базисном периоде
$
в отчетном периоде
$
Т. е. прирост цен на акции компании в среднем составил 12,57%.
При втором варианте используется количество акций:
Т. е. прирост составил 4,44%.
Используя третий метод, рассчитаем средний арифметический темп прироста цен акций:
Это значит, что средний прирост цен акций составил 8,33%.
И наконец, с помощью средней геометрической получим следующий результат:
средний темп прироста составил 7,84%.
Таким образом, все исчисления величины характеризуют однонаправленную тенденцию курса акций и увеличение, хотя имеет место довольно значительная вариация в величине индексов. Главное назначение интегральных показателей - выявить основное направление, основную тенденцию движения курса акций на рынке для характеристики деловой активности в экономике.
В условиях перехода к рыночной экономике большое практическое значение приобретает анализ динамики цен на товары и услуги. Это обусловлено тем, что показатели, характеризующие инфляционные процессы на рынке потребительских товаров применяются при решении многих актуальных экономических задач.

Нравится материал? Поддержи автора!
Ещё документы из категории математика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ