Реферат на тему:

Інтегрування і пониження порядку деяких ДР

з вищими похідними.

1. ДР що містять n-ту похідну від шуканої функції і незалежну змінну.

а) Розглянемо ДР 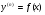(4.38)

Так як 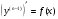, то

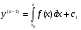
Аналогічно , …..,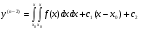

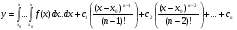(4.39)

Остання формула дає розвязок загальний в області

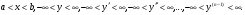
Формулу (4.39) легко використати для знаходження розвязків задачі Коші з начальними умовами

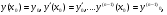(4.40)

Цей розвязок представляється в вігляді 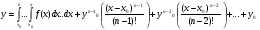(4.41)

Ф-я

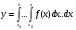
являється частиним розвязком ДР (4.38) з початковими умовами

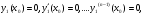
яким відповідають константи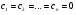

Для обчислення використовують ф-лу Коші

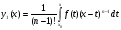(4.42)

Дійсно інтеграл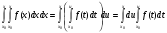

можна розглядати як повторний інтеграл в заштрихованій області (мал. 1).

Міняючи порядок інтегрування, отримаємо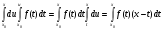

Аналогічно обчислюємо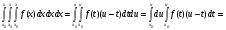

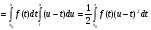.. і. т. д.

Приходимо до ф-ли (4.42)

Таким чином розвязок (4.41) записується у вигляді

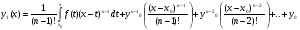
Загальний розвязок ДР (4.38) можна також записати через невизначений інтеграл

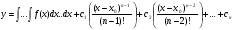
Пр. 4.4 Розвязати рівняння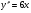

Послідовно знаходимо ,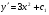

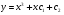
б) Розглянемо випадок 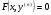(4.43)

в якому співвіднощення (4.43) не можна розвязати відносно 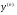в елементарних ф-ях, або вирази для 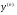будуть досить складними.

Припустимо, що ДР (4.43) допускає параметризацію (4.44)

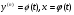(4.44),

де 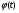та 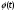такі, що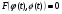

Проводимо обчислення ,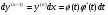

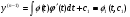
Аналогічно обчислюємо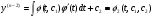

Остаточно маємо

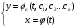(4.45) -загальний зорвязок в параметричній формі.

Відмітимо два випадки, в яких ДР (4.43) легко параметрмзується

I.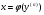(4.46)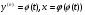(частинні випадки )

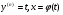II. 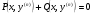(4.47), де 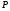і 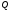-однорідні ф-ї відповідного

виміру 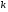і .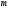

Покладемо 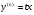(4.48)

і розвяжемо р-ня (4.47) відносно 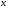через :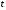

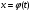
Піставляючи в (4.48), отримаємо 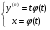(4.49)

Дальше вищеотриманим способом знаходимо загальний розвязок в параметричній формі.

Пр. 4.5 Розвязати р-ня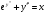

Зробимо заміну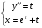

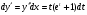
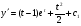
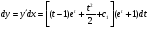остаточно маємо

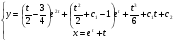
2. Інтегрування ДР, які не містять шуканої ф-ї та 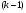похідної.

Розглянемо ДР 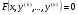(4.50), в якому є .

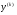Введемо нову змінну 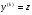(4.51)

отримаємо 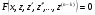(4.52)

тобто ми понизили порядок ДР (4.50) на 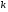одиниць.

Припустимо, що ми розвязали ДР (4.52) і визначили 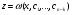(4.53)

Тоді р-ня 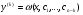(4.54)

інтегруємо і отримаємо загальний розвязок 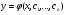(4.55)

Якщо замість загального розвязку (4.53) можна знайти загальний інтеграл 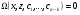(4.54)

то отримаємо ДР 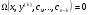типу (4.43)

Розглянемо два частичних випадка відносно ДР (4.50) :

а) ДР вигляду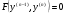

якщо ДР (4.51) можна розвязати відносно :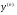

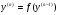(4.52)

то поклавши 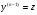перейдемо до р-ня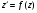

Якщо 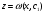- загальний розвязок останнього р-ня, то остотаточно маємо р-ня вигляду (4.38)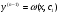

Припустимо, що ДР (4.51) не можна записати в вигляді (4.52), але воно допускає параметризацію 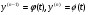(4.53)

то з співвідношення 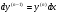знаходимо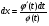

Звідки 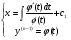(4.54)

ДР (4.54) вигляду (4.44) і розвязки можна отримати в параметричній формі.

б) ДР вигляду 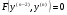(4.55)

Нехай ДР (4.55) можно розвязати відносно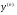

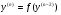(4.56)

Позначимо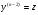 і перейдемо до ДР 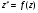(4.57)

Домножимо (4.57) на :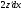

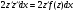
Звідки 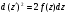. Отже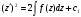

з якого визначимо

.

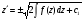Останнє ДР є р-ням з відокремлюваними змінними.

Знайшовши з нього

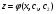
ми остаточно переходимо до ДР вигляду (4.38).

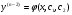(4.58)

Припустимо, що ДР (4.55) не можна розвязати відносно 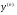але для нього можлива параметризація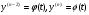

Запишемо співвідношення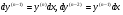

Домножимо першу рівність на :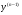

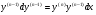
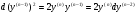
Звідки.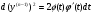

Отже маємо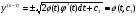

Прийшовши до отсанньої рівності 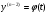ми отримаємо а)

3. Пониження порядку ДР які не містять незалежної змінної.

Ці ДР мають вигляд 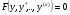(4.59)

і його можна понизити на один порядок заміною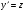

При цьому 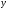стане незалежною зміною, а - функцією

Обчислюємо

…..

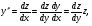
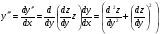
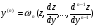
і остаточно прийдемо до ДР 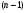порядку

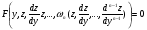
Якщо 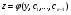- розвязок ДР (4.60) то

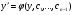
Інтегруємо ДР (4.61) і знайдемо загальний інтеграл.

Особливі зорвязки можуть появлятися при інтегруванні ДР (4.61). При переході до ДР (4.60) ми можимо загубити розвязки .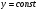

Для їх знаходження необхідно розвявати р-ня .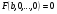

Якщо 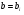- розвязок однорідного р-ня, то 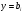- розвязок ДР (4.59)

Пр. 4.6 Розвязати р-ня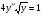

Вводимо змінну , ,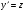

,

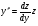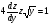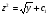
звідки 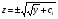, отже, ,

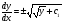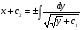
-загальний інтергал рівняння.

4. Однорідні ДР відносно шуканої ф-ї та її похідних.

Так називаються ДР вигляду 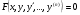в якому 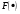являється однорідною ф-єю відносно 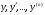, тобт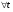о маємо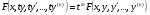

Шляхом заміни 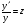ДР (4.62) можна понизити на один порядок.

Обчислюємо

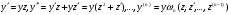
Тому ДР (4.62) прийме вигляд

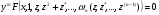(4.63)

Скорочуючи на 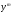( 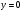при 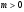може бути розвязком ДР (4.62)), перейдемо до ДР порядку .

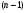Якщо 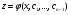– загальний розвязок останнього ДР, то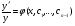

звідки 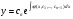(4.64) – загальний розвязок ДР (4.62). Розвязок міститься в формулі (4.64) при .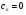

Пр 4.7 Знайти загальний розвязок ДР

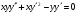
Це ДР являється однорідним відносно шуканої ф-ї і її похідних, тому .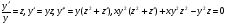

Маємо ДР Бернулі – .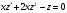

Інтегруючи отрімаємо 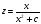, 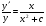Звідки 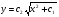. Наше ДР має розвязок 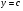який не міститься в знайденому загальному інтергалі.

4. ДР, ліва частина якого є точна похідна.

Припустимо, що ДР (4.62), його ліва частина, є точна похідна по 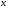від деякої ф-ї 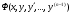, тобто ,

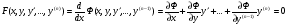тоді ДР (4.62) має перший інтерграл 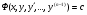(4.64) так, що яого порядок можна понизити на одиницю.

Пр 4.8 Розвязати ДР

Маємо 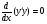, ,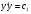, 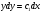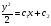– загальний інтеграл. Якщо ліва частина ДР (4.62) не являється точною похідною, то в деяких випадках можна знайти ф-ю 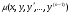, після домноження на яку р-ня (4.62), його ліва частина буде точною похідною. Ця ф-я називається інтергрувальним множником. Якщо ми знаємо ф-ю 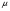, то можна знайти не тільки перший інтеграл, а й особливі розвязки, які знаходяться з р-ня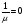

Пр 4.9 Знайти загальний розвязок ДР .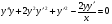

Візьмемо 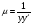, тоді .

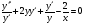При цьому 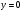, 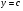- розвязки нашого ДР.

Маємо .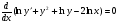

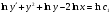- перший інтерал.

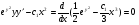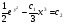, загальний інтергал.

Особливих розвязків немає, так як ДР 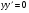приводіть до розвязків 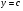, які містяться в загальному.