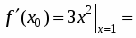
ВЫСШАЯ МАТЕМАТИКА

ИССЛЕДОВАНИЕ ФУНКЦИЙ

СОДЕРЖАНИЕ

1. Основные теоремы дифференциального исчисления

1.1 Локальные экстремумы функции

1.2 Основные теоремы дифференциального исчисления: Ферма, Ролля, Коши, Лагранжа

2. Исследование функций

2.1 Достаточные условия экстремума функции

2.2 Исследование функций на выпуклость и вогнутость. Точка перегиба

2.3 Асимптоты графика функции

2.4 Общая схема построения графика функции

Литература

1. ОСНОВНЫЕ ТЕОРЕМЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ

1.1 Локальные экстремумы функции

Пусть задана функция у = f (х) на множестве Х и х₀ – внутренняя точка множества Х.

Обозначим через U(х₀) окрестность точки х₀. В точке х₀ функция f (х) имеет локальный максимум, если существует такая окрестность U(х₀) точки х₀, что для всех х из этой окрестности выполнено условие f (х)  f (х₀).

Аналогично: функция f (х) имеет в точке х₀ локальный минимум, если существует такая окрестность U(х₀) точки х₀, что для всех х из этой окрестности выполнено условие f (х)  f (х₀).

Точки локальных максимума и минимума называются точками локальных экстремумов, а значения функции в них – локальными экстремумами функции.

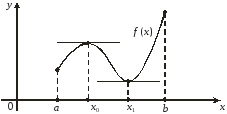
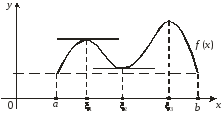
Пусть функция f (х) определена на отрезке [а, b] и имеет локальный экстремум на каком-то из концов этого отрезка. Тогда такой экстремум называется локальным односторонним или краевым экстремумом. В этом случае соответствующая окрестность является правой для «а» и левой для «b» полуокрестностью.

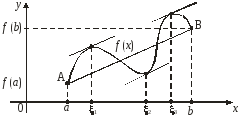
Проиллюстрируем данные выше определения:

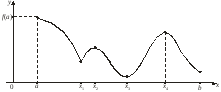
На рисунке точки х₁, х₃ – точки локального минимума, точки х₂, х₄ – точки локального максимума, х = а – краевого максимума, х = b – краевого минимума.

Заметим, что наряду с локальными минимумом и максимумом определяют так называемые глобальные минимумы и максимумы функции f(х) на отрезке [a, b]. На рисунке точка х = а – точка глобального максимума (в этой точке функция f(х) принимает наибольшее значение на отрезке [a, b]), точка х = х₃ – точка соответственно глобального минимума.

1.2 Основные теоремы дифференциального исчисления: Ферма, Ролля, Коши, Лагранжа

Рассмотрим некоторые теоремы, которые позволят в дальнейшем проводить исследование поведения функций. Они носят названия основных теорем математического анализа или основных теорем дифференциального исчисления, поскольку указывают на взаимосвязь производной функции в точке и ее поведения в этой точке. Рассмотрим теорему Ферма.

Пьер Ферма (1601–1665) – французский математик. По профессии – юрист. Математикой занимался в свободное время. Ферма – один из создателей теории чисел. С его именем связаны две теоремы: великая теорема Ферма (для любого натурального числа n > 2 уравнение хⁿ + yⁿ = zⁿ не имеет решений в целых положительных числах х, у, z) и малая теорема Ферма (если р – простое число и а – целое число, не делящееся на р, то а ^р-1 – 1 делится на р).

Теорема Ферма. Пусть функция f (х) определена на интервале (а, b) и в некоторой точке х₀  (а, b) имеет локальный экстремум. Тогда, если в точке х₀ существует конечная производная f '(x₀), то f '(x₀) = 0.

Доказательство.

Пусть, для определенности, в точке х₀ функция имеет локальный минимум, то есть f (х)  f (х₀), х  U(х₀). Тогда в силу дифференцируемости

f (х) в точке х₀ получим:

при х > х₀:

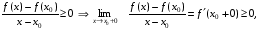
при х < х₀:

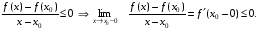
Следовательно, эти неравенства в силу дифференцируемости имеют место одновременно лишь когда

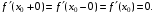
Теорема доказана.

Геометрический смысл теоремы Ферма: если х₀  (а, b) является точкой минимума или максимума функции f (х) и в этой точке существует производная функции, то касательная, проведенная к графику функции в точке (х₀, f (х₀)), параллельна оси Ох:

Заметим, что оба условия теоремы Ферма – интервал (а, b) и дифференцируемость функции в точке локального экстремума – обязательны.

Пример 1. у = х, х  (–1; 1).

В точке х₀ = 0 функция имеет минимум, но в этой точке производная не существует. Следовательно, теорема Ферма для данной функции неверна (не выполняется условие дифференцируемости функции в точке х₀).

Пример 2. у = х³, х  [–1; 1].

В точке х₀ = 1 функция имеет краевой максимум. Теорема Ферма не выполняется, так как точка х₀ = 1  (–1; 1).

Мишель Ролль (1652–1719) – французский математик, член Парижской академии наук. Разработал метод отделения действительных корней алгебраических уравнений.

Теорема Ролля. Пусть функция f (x) непрерывна на отрезке [а, b], дифференцируема на (а, b), f (а) = f(b). Тогда существует хотя бы одна точка , а <  < b, такая, что f '() = 0.

Доказательство:

1) если f (x) = const на [a, b], то f '(х) = 0, х  (a, b);

2) если f (x)  const на [a, b], то непрерывная на [a, b] функция достигает наибольшего и наименьшего значений в некоторых точках отрезка

[a, b]. Следовательно, max f (x) или min f (x) обязательно достигается во внутренней точке  отрезка [a, b], а по теореме Ферма имеем, что f '() = 0.

Теорема доказана.

Геометрический смысл теоремы Ролля: при выполнении условий теоремы внутри отрезка [a, b] обязательно найдется хотя бы одна точка , такая, что касательная к графику f (x) в точке (, f ())  Ox (см. рисунок).

Заметим, что все условия теоремы существенны.

Пример 3. f (x) = х, х  [-1; 1]. f (-1) = f (1) = 1.

В точке х = 0 нарушено условие дифференцируемости. Следовательно, теорема Ролля не применяется – ни в одной точке отрезка [–1; 1] производная в нуль не обращается.

Пример 4.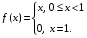

Для данной функции f(0) = f(1) = 0, но ни в одной точке интервала

(0; 1) производная не равна 0, так как теорема Ролля не выполняется – функция не является непрерывной на [0; 1].

Огюстен Коши (1789–1857) – французский математик, член Парижской академии наук, почетный член Петербургской и многих других академий. Труды Коши относятся к математическому анализу, дифференциальным уравнениям, алгебре, геометрии и другим математическим наукам.

Теорема Коши. Пусть функции f (х) и g(х) непрерывны на отрезке

[a, b] и дифференцируемы на интервале (a, b), причем g'(х)  0, х  (a, b). Тогда на (a, b) найдется точка , такая, что

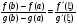. (1)

Доказательство.

Рассмотрим вспомогательную функцию 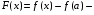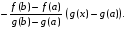Функция F(х) непрерывна на [a, b], дифференцируема на (a, b), причем F(а) = F(b) = 0. Следовательно, по теореме Ролля на (a, b) существует точка , такая, что F'() = 0:

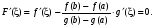
Следовательно:

.

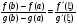Теорема доказана.

Жозеф Луи Лагранж (1736–1813) – французский математик и механик, почетный член Парижской и Петербургской академий. Ему принадлежат выдающиеся исследования по математическому анализу, по различным вопросам дифференциальных уравнений, по алгебре и теории чисел, механике, астрономии. Лагранж впервые ввел в рассмотрение тройные интегралы, предложил обозначения для производной (y', f '(x)).

Теорема Лагранжа. Пусть функция f(х) непрерывна на [a, b], дифференцируема на интервале (a, b). Тогда на (a, b) найдется точка , такая, что

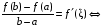
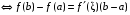(2)

Доказательство.

Из формулы (1) при g(x) = x получаем формулу (2).

Теорема доказана.

Равенство (2) называют формулой конечных приращений или формулой Лагранжа о среднем.

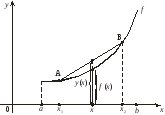
Геометрический смысл теоремы Лагранжа.

При выполнении условий теоремы внутри отрезка [a, b] обязательно найдется хотя бы одна точка , такая, что касательная к графику функции f (x) в точке (, f ()) параллельна секущей, проходящей через точки А (а, f (а)) и В (b, f(b)) (см. рисунок).

Рассмотрим следствия из теоремы Лагранжа:

1. (условие постоянства функции на отрезке). Пусть функция f (x) непрерывна на [a, b], дифференцируема на (a, b). Если f '(x) = 0, х  (a, b), то функция f (x) постоянна на [a, b].

2. Пусть функции f (x) и g(х) непрерывны на отрезке [a, b], дифференцируемы на интервале (a, b), f '(x) = g'(х), х  (a, b). Тогда f (x) = g(х) + С, где С = const.

3. (условие монотонности функции). Пусть функция f(x) непрерывна на отрезке [a, b], дифференцируемая на интервале (a, b). Тогда, если f '(x) > 0, х  (a, b), то f (x) строго монотонно возрастает на (a, b). Если же f '(x) < 0,

х  (a, b), то f (x) строго монотонно убывает на (a, b).

2. ИССЛЕДОВАНИЕ ФУНКЦИЙ

2.1 Достаточные условия экстремума функции

В лекции 1 мы рассмотрели основные теоремы математического анализа, которые широко используются при исследовании функции, построении ее графика.

По теореме Ферма: из дифференцируемости функции f (x) в точке локального экстремума х₀ следует, что f '(x₀) = 0. Данное условие является необходимым условием существования в точке локального экстремума, то есть если в точке х₀ – экстремум функции f (x) и в этой точке существует производная, то f '(x₀) = 0. Точки х₀, в которых f '(x₀) = 0, называются стационарными точками функции. Заметим, что равенство нулю производной

в точке не является достаточным для существования локального экстремума в этой точке.

Пример 1. у = х³, у' = 3х², у'(0) = 0, но

в точке х₀ = 0 нет экстремума.

Точками, подозрительными на экстремум функции f (x) на интервале (a, b), являются точки, в которых производная существует и равна 0 либо она не существует или равна бесконечности. На рисунках функции имеют минимум в точке х₀ = 0:

f '(0) = 0 f '(0)  f '(0) = 

Рассмотрим достаточные условия существования в точке локального экстремума, которые позволят ответить на вопрос: «Есть ли в точке экстремум и какой именно – минимум или максимум?».

Теорема 1 (первое достаточное условие экстремума). Пусть непрерывная функция f (x) дифференцируема в некоторой проколотой окрестности U(x₀) точки х₀ (проколотая окрестность означает, что сама точка х₀ выбрасывается из окрестности) и непрерывна в точке х₀. Тогда:

1) если 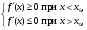(1)

то в точке х₀ – локальный максимум;

2) если 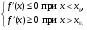(2)

то в точке х₀ – локальный минимум.

Доказательство.

Из неравенств (1) и следствия 3 теоремы Лагранжа (о монотонности функции) следует, что при х < х₀ функция не убывает, а при х > х₀ функция не возрастает, то есть

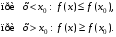(3)

Следовательно, из (3) получаем, что в точке х₀ функция имеет локальный максимум.

Аналогично можно рассмотреть неравенства (2) для локального минимума:

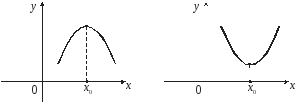
f (x) f (x)

f '(х)  0 f '(х)  0 f '(х)  0 f '(х)  0

Теорема доказана.

Пример 2. Исследовать на монотонность и локальный экстремум функцию 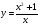с помощью производной первого порядка.

Решение. Найдем стационарные точки функции:

 х² –1 = 0  х₁ = –1, х₂ = 1.

Заметим, что данная функция не определена в точке х = 0. Следовательно:

х

(–; –1)

–1

(–1; 0)

0

(0; 1)

1

(1; +)

у'

+

0

–

–

–

0

+

у

–2

–

2

max min

То есть функция 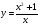возрастает на интервалах (–; –1) и (1; +), убывает на интервалах (–1; 0), (0; 1), имеет локальный максимум в точке

х₁ = –1, равный у_max (–1) = –2; имеет локальный минимум в точке х₂ = 1,

у_min (1) = 2.

Теорема 2 (второе достаточное условие экстремума). Пусть функция f (x) дважды непрерывно-дифференцируема. Если х₀ – стационарная точка

(f ' (х₀) = 0), в которой f '' (х₀) > 0, то в точке х₀ функция имеет локальный минимум. Если же f '' (х₀) < 0, то в точке х₀ функция имеет локальный максимум.

Доказательство. Пусть для определенности f '' (х₀) > 0. Тогда

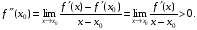
Следовательно:

при х < х₀, f ' (х) < 0,

при х > х₀, f ' (х) > 0.

Поэтому по теореме 1 в точке х₀ функция имеет локальный минимум.

Теорема доказана.

Пример 3. Исследовать на экстремум функцию 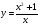с помощью второй производной.

Решение. В примере 2 для данной функции мы нашли первую производную 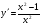и стационарные точки х₁ = –1, х₂ = 1.

Найдем вторую производную данной функции:

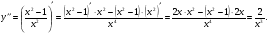
Найдем значения второй производной в стационарных точках.

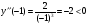 в точке х₁ = –1 функция имеет локальный максимум;

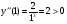 в точке х₂ = 1 функция имеет локальный минимум (по теореме 2).

Заметим, что теорема 1 более универсальна. Теорема 2 позволяет проанализировать на экстремум лишь точки, в которых первая производная равна нулю, в то время как теорема 1 рассматривает три случая: равенство производной нулю, производная не существует, равна бесконечности в подозрительных на экстремум точках.

2.2 Исследование функций на выпуклость и вогнутость. Точка перегиба

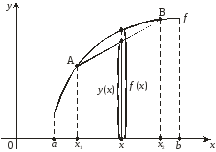
Пусть функция f (х) задана на интервале (a, b) и х₁, х₂ – любые различные точки этого интервала. Через точки А (х₁, f (х₁)) и В (х₂, f (х₂)) графика функции f (х) проведем прямую, отрезок АВ которой называется хордой. Уравнение этой прямой запишем в виде у = у(х).

Функция f (х) называется выпуклой вниз на интервале (a, b), если для любых точек х₁, х₂  (a, b), а  х₁ < х₂  b, хорда АВ лежит не ниже графика этой функции, т. е. если f (х)  у (х),  х  [х₁, х₂]  (a, b):

Заметим, что выпуклую вниз функцию иногда называют вогнутой функцией. Аналогично определяется выпуклость функции вверх.

Функция f (х) называется выпуклой вверх на интервале (a, b), если для любых точек х₁, х₂  (a, b), а  х₁ < х₂  b, хорда АВ лежит не выше графика этой функции, т. е. если f (х)  у (х),  х  [х₁, х₂]  (a, b):

Теорема 3 (достаточное условие выпуклости). Если f (х) – дважды непрерывно дифференцируема на интервале (a, b) и

1) f ''(х) > 0,  х  (a, b), то на (a, b) функция f (х) выпукла вниз;

2) f ''(х) < 0,  х  (a, b), то на (a, b) функция f (х) выпукла вверх.

Точка х₀ называется точкой перегиба функции f (х), если   – окрест-ность точки х₀, что для всех х  (х₀ – , х₀) график функции находится с одной стороны касательной, а для всех х  (х₀, х₀ + ) – с другой стороны каса-тельной, проведенной к графику функции f (х) в точке х₀, то есть точка х₀ – точка перегиба функции f (х), если при переходе через точку х₀ функция f (х) меняет характер выпуклости:

х₀ –  х₀ х₀ + 

Теорема 4 (необходимое условие существования точки перегиба). Если функция f (х) имеет непрерывную в точке х₀ производную f '' и х₀ – точка перегиба, то f '' (х₀) = 0.

Доказательство.

Если бы f '' (х₀) < 0 или f '' (х₀) > 0, то по теореме 3 в точке х₀ функция f (х) была бы выпукла вверх или вниз. Следовательно, f ''(х₀) = 0.

Теорема доказана.

Теорема 5 (достаточное условие перегиба). Если функция f (х) дважды непрерывно дифференцируема в окрестности точки х₀ и при переходе через точку х₀ производная f ''(х) меняет знак, то точка х₀ является точкой перегиба функции f (х).

Пример 4. Исследовать на выпуклость и найти точки перегиба функции у = х³.

Решение. у' = 3х², у'' = 6х = 0  х₀ = 0 – точка, подозрительная на перегиб.

В точке х₀ = 0 функция у = х³ имеет перегиб:

х

(–; 0)

0

(0; +)

у''

–

0

+

у

выпукла вверх

0

выпукла вниз

точка перегиба

Пример 5. Исследовать на выпуклость и найти точки перегиба функции .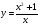

Решение. В примере 3 мы уже находили вторую производную данной функции . Так как то точек подозрительных на перегиб нет. Рассмотрим промежутки выпуклости:

х

(–; 0)

0

(0; +)

у''

–

–

+

у

выпукла вверх

–

выпукла вниз

функция не определена

2.3 Асимптоты графика функции

Асимптотой будем называть прямую, к которой график функции неограниченно близко приближается. Различают вертикальные и наклонные асимптоты.

Прямая х = х₀ называется вертикальной асимптотой графика функции f (х), если хотя бы один из пределов f (х₀ – 0) или f (х₀ + 0) равен бесконечности.

Пример 6. Найти вертикальные асимптоты функций:

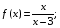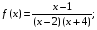а) б) в)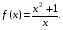

Решение. Вертикальными асимптотами функций будут прямые х = х₀, где х₀ – точки, в которых функция не определена.

а) х = 3 – вертикальная асимптота функции 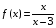. Действительно, ;

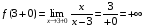б) х = 2, х = – 4 – вертикальные асимптоты функции 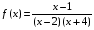. Действительно,

,

;

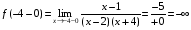в) х = 0 – вертикальная асимптота функции 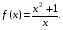Действительно, .

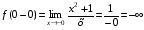Прямая у = kx + b называется наклонной асимптотой графика непрерывной функции f (х) при х  + или х  – , если f (х) = kx + b + α(х), 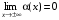, то есть если наклонная асимптота для графика функции f (х) существует, то разность ординат функции f (х) и прямой у = kx + b в точке х стремится к 0 при х  + или при х  – .

Теорема 6. Для того чтобы прямая у = kx + b являлась наклонной асимптотой графика функции f (х) при х  + или х  – , необходимо и достаточно существование конечных пределов:

(4)

Следовательно, если хотя бы один из данных пределов не существует или равен бесконечности, то функция не имеет наклонных асимптот.

Пример 7. Найти наклонные асимптоты функции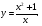

Решение. Найдем пределы (4):

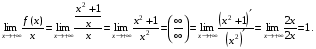
Следовательно, k = 1.

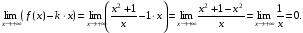
Следовательно, b = 0.

Таким образом, функция 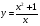имеет наклонную асимптоту

у = kx + b = 1 · х + 0 = х.

Ответ: у = х – наклонная асимптота.

Пример 8. Найти асимптоты функции .

Решение.

а) функция неопределенна в точках х₁ = –1, х₂ = 1. Следовательно, прямые х₁ = –1, х₂ = 1 – вертикальные асимптоты данной функции.

Действительно, .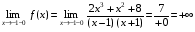

;

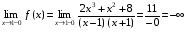б) у = kx + b.

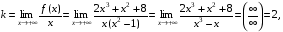
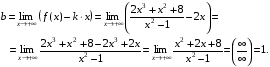
Следовательно, у = 2х + 1 – наклонная асимптота данной функции.

Ответ: х₁ = –1, х₂ = 1 – вертикальные, у = 2х + 1 – наклонная асимп-

тоты.

2.4 Общая схема построения графика функции

1. Находим область определения функции.

2. Исследуем функцию на периодичность, четность или нечетность.

3. Исследуем функцию на монотонность и экстремум.

4. Находим промежутки выпуклости и точки перегиба.

5. Находим асимптоты графика функции.

6. Находим точки пересечения графика функции с осями координат.

7. Строим график.

Прежде чем перейти к примерам, напомним определения четности и нечетности функции.

Функция у = f (х) называется четной, если для любого значения х, взятого из области определения функции, значение (–х) также принад-лежит области определения и выполняется равенство f (х) = f (–х). График четной функции симметричен относительно оси ординат.

Функция у = f (х) называется нечетной для любого значения х, взятого из области определения функции, значение (–х) также принадлежит об-ласти определения, и выполняется равенство f (–х) = –f (х). График не-четной функции симметричен относительно начала координат.

Пример 9. Построить график .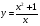

Решение. Мы используем данные, полученные для этой функции в других примерах.

1. D (у) = (–; 0)  (0; +).

2. 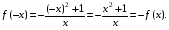Следовательно, функция нечетная. Ее график будет симметричен относительно начала координат.

3. (см. пример 2). Исследуем функцию на монотонность и экстремум:

х

(–; –1)

–1

(–1; 0)

0

(0; 1)

1

(1; +)

у'

+

0

–

–

–

0

+

у

–2

–

2

max min

4. (см. пример 5). Исследуем функцию на выпуклость и найдем точки перегиба.

х

(–; 0)

0

(0; +)

у''

–

–

+

у

выпукла вверх

–

выпукла вниз

функция не определена

Несмотря на то, что функция поменяла характер выпуклости при переходе через точку х = 0, но в ней нет перегиба, так как в этой точке функция не определена.

5. (см. примеры 6 и 7). Найдем асимптоты функции:

а) х = 0 – вертикальная асимптота;

б) у = х – наклонная асимптота.

6. Точек пересечения с осями координат у данной функции нет, так как 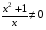, при любых х  , а х = 0  D(у).

7. По полученным данным строим график функции:

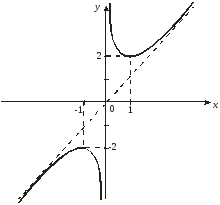
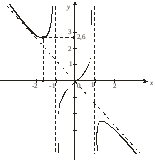
Пример 10. Построить график функции .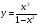

Решение.

1. D(у) = (–; –1)  (–1; 1)  (1; +).

2. 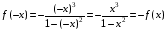– функция нечетная. Следовательно, график функции будет симметричен относительно начала координат.

3. Исследуем функцию на монотонность и экстремум:

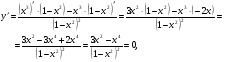
3х² – х⁴ = 0, х² · (3 – х²) = 0, х₁ = 0, х₂ = 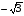, х₃ = .

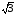х

(–;)

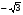(; 0)

–1

(–1; 0)

0

(0; 1)

1

(1; )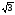

(; +)

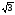
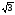у'

–

0

+

–

+

0

+

–

+

0

–

у

2,6

–

0

–

–2,6

4. Исследуем функцию на выпуклость и точки перегиба:

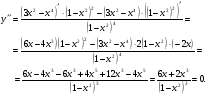
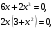
х = 0 – точка, подозрительная на перегиб.

х

(–; –1)

–1

(–1; 0)

0

(0; 1)

1

(0; +)

у''

+

–

–

0

+

–

–

у

выпукла

вниз

–

выпукла

вверх

0

выпукла вниз

–

выпукла

вниз

перегиб

5. Найдем асимптоты функции:

а) х = –1, х = 1 – вертикальные асимптоты.

Действительно:

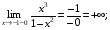
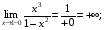
б) у = kx + b.

,

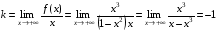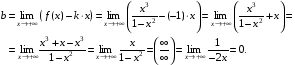
 у = –1х + 0 = – х – наклонная асимптота.

6. Найдем точки пересечения с осями координат:

х = 0  у = 0  (0; 0) – точка пересечения с осями координат.

7. Строим график:

ЛИТЕРАТУРА

1. Гусак А. А. Математический анализ и дифференциальные уравнения.– Мн.: Тетрасистемс, 1998. – 415 с.

2. Минченков Ю. В. Высшая математика. Производная функции. Дифференциал функции: Учебно-методическое пособие.– Мн.: ЧИУиП, 2007.– 20 с.