Федеральное агентство по образованию

Всероссийский заочный финансово-экономический институт

Кафедра экономико-математических методов и моделей

КОНТРОЛЬНАЯ РАБОТА

по дисциплине «Эконометрика»

Вариант № 3

Исполнитель: Глушакова Т.И.

Специальность: Финансы и кредит

Курс: 3

Группа: 6

№ зачетной книжки: 07ффд41853

Руководитель: Денисов В.П.

г. Омск 2009г.

Задачи

По предприятиям легкой промышленности региона получена информация, характеризующая зависимость объема выпуска продукции (Y, млн. руб.) от объема капиталовложений (X, млн. руб.). Требуется:

1. Найти параметры уравнения линейной регрессии, дать экономическую интерпретацию коэффициента регрессии.

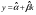- уравнение линейной регрессии, где - параметры уравнения.

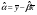, где 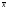, 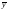- средние значения признаков.

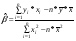, где n – число наблюдений.

Представим вычисления в таблице 1:

Таблица 1. Промежуточные расчеты.

t

xi

yi

yi * xi

xi*xi

1

38

69

2622

1444

2

28

52

1456

784

3

27

46

1242

729

4

37

63

2331

1369

5

46

73

3358

2116

6

27

48

1296

729

7

41

67

2747

1681

8

39

62

2418

1521

9

28

47

1316

784

10

44

67

2948

1936

средн. знач.

35,5

59,4

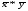
2108,7

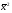
1260,25

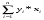
21734

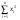
13093

n

10

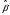
1,319

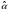
12,573

Таким образом, уравнение линейной регрессии имеет вид:

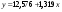
Коэффициент регрессии равен 1,319>0, значит связь между объемом капиталовложений и выпуском продукции прямая, увеличение объема капиталовложений на 1 млн. руб. ведет к увеличению объема выпуска продукции в среднем на 1,319 млн. руб. Это свидетельствует об эффективности работы предприятий.

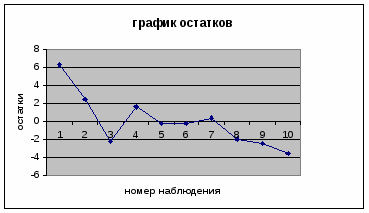
2. Вычислить остатки; найти остаточную сумму квадратов; оценить дисперсию остатков 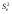; построить график остатков.

Вычислим прогнозное значение Y по формуле:

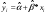
Остатки вычисляются по формуле:

.

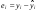Представим промежуточные вычисления в таблице 2.

Таблица 2. Вычисление остатков.

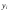
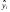
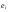
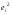
69

62,695

6,305

39,75303

52

49,505

2,495

6,225025

46

48,186

-2,186

4,778596

63

61,376

1,624

2,637376

73

73,247

-0,247

0,061009

48

48,186

-0,186

0,034596

67

66,652

0,348

0,121104

62

64,014

-2,014

4,056196

47

49,505

-2,505

6,275025

67

70,609

-3,609

13,02488

Дисперсия остатков вычисляется по формуле:

.

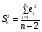
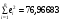
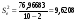Построим график остатков с помощью MS Excel.

Рис. 1. График остатков.

3. Проверить выполнение предпосылок МНК

Проверим независимость остатков с помощью критерия Дарбина-Уотсона.

Вычислим коэффициент Дарбина-Уотсона по формуле:

.

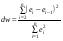Данные для расчета возьмем из таблицы 2.

dw = 0,803

Сравним полученное значение коэффициента Дарбина-Уотсона с табличными значениями границ 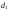и 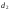для уровня значимости 0,05 при k=1 и n=10. 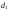=0,88, 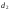=1,32, dw < d , значит, остатки содержат автокорреляцию. Наличие автокорреляции нарушает одну из предпосылок нормальной линейной модели регрессии.

Проверим наличие гетероскедастичности. Т.к. у нас малый объем выборки (n=10) используем метод Голдфельда-Квандта.

- упорядочим значения n наблюдений по мере возрастания переменной x и разделим на две группы с малыми и большими значениями фактора x соответственно.

- рассчитаем остаточную сумму квадратов для каждой группы.

Вычисления представим в таблицах 3 и 4.

Таблица 3. Промежуточные вычисления для 1-го уравнения регрессии.

t

xi

yi

yi * xi

xi*xi

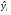
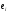
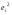
1

27

46

1242

729

47

-1

1

2

27

48

1296

729

47

1

1

3

28

47

1316

784

49,5

-2,5

6,25

4

28

52

1456

784

49,5

2,5

6,25

средн. знач.

27,5

48,25

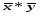
1326,875

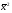
756,25

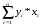
5310,00

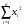
3026,00

n

4

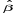
2,5

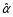
- 20,5

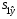
14,5

Таблица 4. Промежуточные вычисления для 2-го уравнения регрессии.

t

xi

yi

yi * xi

xi*xi

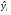
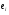
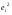
1

37

63

2331

1369

63,789

-0,789

0,623

2

38

69

2622

1444

64,582

4,418

19,519

3

39

62

2418

1521

65,375

-3,375

11,391

4

41

67

2747

1681

66,961

0,039

0,002

5

44

67

2948

1936

69,340

-2,340

5,476

6

46

73

3358

2116

70,926

2,074

4,301

средн. знач.

40,833

66,833

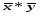
2729,028

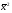
1667,361

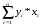
16424

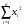
10067

n

6

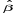
0,793

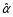
34,448

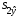
41,310

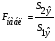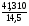= =2,849

где 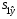- остаточная сумма квадратов 1-ой регрессии, 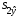- остаточная сумма квадратов 2-ой регрессии.

Полученное значение сравним с табличным значением F распределения для уровня значимости 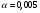, со степенями свободы 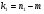и 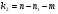( 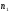- число наблюдений в первой группе, m – число оцениваемых параметров в уравнении регрессии).

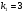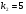, , m=1.

Если 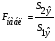> 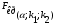, то имеет место гетероскедастичность.

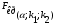= 5,41

< ,

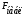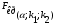значит, гетероскедастичность отсутствует и предпосылка о том, что дисперсия остаточных величин постоянна для всех наблюдений выполняется.

4. Осуществить проверку значимости параметров уравнения регрессии с помощью t-критерия Стьюдента .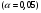

Расчетные значения t-критерия можно вычислить по формулам:

,

,

,

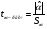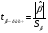
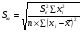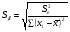
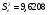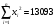
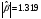
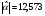
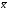=35,5

Промежуточные расчеты представим в таблице:

Таблица 5. Промежуточные вычисления для расчета t- критерия

xi

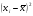
38

6,25

28

56,25

27

72,25

37

2,25

46

110,25

27

72,25

41

30,25

39

12,25

28

56,25

44

72,25

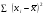=490,50

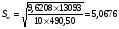
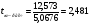
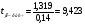
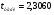для уровня значимости 0,05 и числа степеней свободы n-2=8

Так как 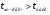и 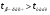можно сделать вывод, что оба коэффициента регрессии значимые.

5. Вычислить коэффициент детерминации, проверить значимость уравнения регрессии с помощью F-критерия Фишера 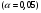, найти среднюю относительную ошибку аппроксимации. Сделать вывод о качестве модели.

Коэффициент детерминации определяется по формуле:

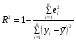
Из расчетов нам известно, что

; .

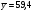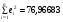Рассчитаем :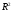

Таблица 6. Промежуточные вычисления для расчета коэффициента детерминации.

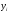
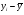
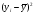
69

9,6

92,16

52

-7,4

54,76

46

-13,4

179,56

63

3,6

12,96

73

13,6

184,96

48

-11,4

129,96

67

7,6

57,76

62

2,6

6,76

47

-12,4

153,76

67

7,6

57,76

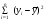=930,4

=0,917.

Т.к. значение коэффициента детерминации близко к единице, качество модели считается высоким.

Теперь проверим значимость уравнения регрессии. Рассчитаем значение F-критерия Фишера 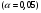по формуле:

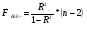
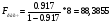
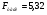
Уравнение регрессии с вероятностью 0,95 в целом статистически значимое, т.к. >.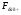

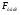Средняя относительная ошибка аппроксимации находится по формуле:

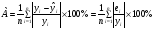
Таблица 7. Промежуточные вычисления для расчета средней относительной ошибки аппроксимации.

yi

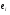
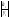
69

6,305

0,091377

52

2,495

0,047981

46

-2,186

0,047522

63

1,624

0,025778

73

-0,247

0,003384

48

-0,186

0,003875

67

0,348

0,005194

62

-2,014

0,032484

47

-2,505

0,053298

67

-3,609

0,053866

,

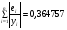
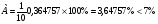значит модель имеет хорошее качество.

Рассчитаем коэффициент эластичности по формуле:

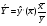
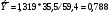
6. осуществить прогнозирование среднего значения показателя Y при уровне значимости 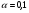, если прогнозное значение фактора X составит 80% от его максимального значения.

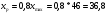
Рассчитаем стандартную ошибку прогноза

,

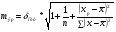где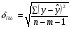

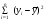=930,4 ;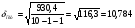

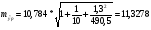
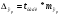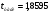, для уровня значимости 0,1 и числа степеней свободы n-2=8

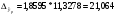
Доверительный интервал прогноза:

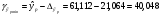
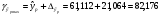
Таким образом, 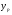=61,112 , будет находиться между верхней границей, равной 82,176 и нижней границей, равной 40,048.

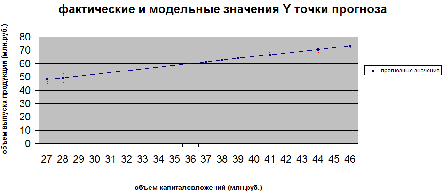
7. Представить графически фактические и модельные значения Y точки прогноза.

Воспользуемся данными из таблицы 2 для построения графиков с помощью MS Excel.

Рис. 2. Фактические и модельные значения Y точки прогноза.

8. Составить уравнения нелинейной регрессии: гиперболической, степенной, показательной. Привести графики построенных уравнений регрессии.

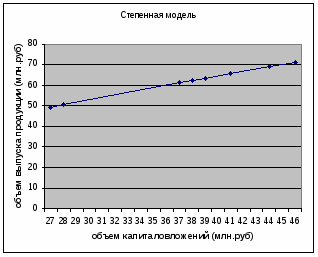
Построение степенной модели.

Уравнение степенной модели имеет вид:

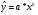
Для построения этой модели необходимо произвести линеаризацию переменных. Для этого произведем логарифмирование обеих частей уравнения:

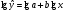
Обозначим .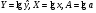

Тогда уравнение примет вид 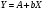– линейное уравнение регрессии. Рассчитаем его параметры, используя данные таблицы 1:

Таблица 8. Расчет параметров уравнения степенной модели регрессии.

t

xi

X

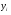
Y

YX

X*X

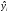
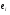
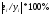
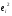
1

38

1,5798

69

1,839

2,905

2,496

62,347

6,653

9,642

44,26

2

28

1,447

52

1,716

2,483

2,094

50,478

1,522

2,926

2,315

3

27

1,431

46

1,663

2,379

2,048

49,225

-3,225

7,010

10,399

4

37

1,568

63

1,799

2,821

2,459

61,208

1,792

2,845

3,212

5

46

1,663

73

1,863

3,098

2,765

71,153

1,847

2,530

3,411

6

27

1,431

48

1,681

2,406

2,049

49,225

-1,225

2,552

1,5

7

41

1,613

67

1,826

2,945

2,601

65,771

1,289

1,924

1,66

8

39

1,591

62

1,793

2,853

2,531

63,477

-1,477

2,382

2,182

9

28

1,447

47

1,672

2,419

2,094

50,478

-3,478

7,4

12,099

10

44

1,644

67

1,826

3,001

2,701

68,999

-1,999

2,984

3,997

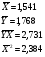
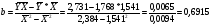
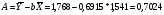
Уравнение регрессии будет иметь вид:

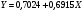
Перейдем к исходным переменным x и y, выполнив потенцирование данного уравнения:

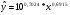
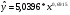
Вычислим коэффициент детерминации :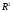

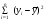=930,4;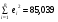

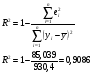(1)

Вычислим среднюю ошибку аппроксимации А:

%

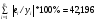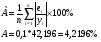(2)

Коэффициент эластичности рассчитывается по формуле:

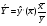(3)

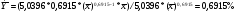
Рис. 3. График степенного уравнения регрессии.

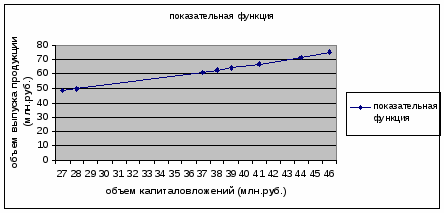
Построение показательной функции.

Уравнение показательной кривой: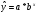

Для построения этой модели необходимо произвести линеаризацию переменных. Для этого осуществим логарифмирование обеих частей уравнения:

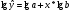
Обозначим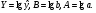

Получим линейное уравнение регрессии:

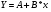
Рассчитаем его параметры, используя данные таблиц 1 и 8.

Промежуточные расчеты представим в таблице 9.

Таблица 9. Промежуточные расчеты для показательной функции.

t

xi

Y

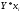
y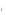

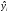
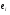
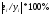
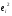
1

38

1,839

69,882

69

62,632

6,368

10,167

40,552

2

28

1,716

48,048

52

49,893

2,107

4,223

4,44

3

27

1,663

44,901

46

48,771

-2,771

5,682

7,68

4

37

1,799

66,563

63

61,224

1,776

2,901

3,155

5

46

1,863

85,698

73

75,128

-2,128

2,832

4,528

6

27

1,681

45,387

48

48,771

-0,771

1,581

0,595

7

41

1,826

74,866

67

67,054

-0,054

0,08

0,003

8

39

1,793

69,927

62

64,072

-2,072

3,235

4,295

9

28

1,672

46,816

47

49,893

-2,893

5,798

8,369

10

44

1,826

80,344

67

71,788

-4,788

6,669

22,921

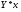=63,2432

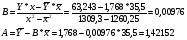
Уравнение будет иметь вид:

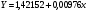
Перейдем к исходным переменным x и y, выполнив потенцирование данного уравнения:

Рассчитаем коэффициент детерминации по формуле (1).

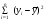=930,4;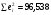

Вычислим среднюю ошибку аппроксимации А по формуле (2):

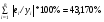
А=0,1*43,170=4,317%

Коэффициент эластичности рассчитаем по формуле (3):

%

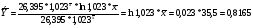Построим график функции с помощью MS Excel.

Рис. 4. График показательного уравнения регрессии.

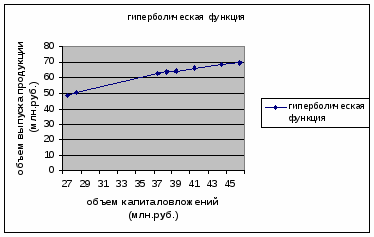
Построение гиперболической функции.

Уравнение гиперболической функции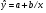

Произведем линеаризацию модели путем замены Х=1/х.

В результате получим линейное уравнение: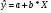

Рассчитаем параметры уравнения, промежуточные вычисления представим в таблице 10.

Таблица 10. Расчет параметров для гиперболической модели.

t

xi

yi

X=1/xi

y*X

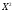
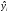
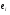
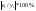
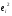
1

38

69

0,02632

1,81579

0,00069

63,5648

5,4352

7,877

29,5409

2

28

52

0,03571

1,85714

0,00128

50,578

1,422

2,7346

2,0221

3

27

46

0,03704

1,7037

0,00137

48,7502

-2,7502

5,9787

7,5637

4

37

63

0,02703

1,7027

0,00073

62,5821

0,4179

0,6634

0,1747

5

46

73

0,02174

1,58696

0,00047

69,8889

3,1111

4,2618

9,6791

6

27

48

0,03704

1,77778

0,00137

48,7502

-0,7502

1,563

0,5628

7

41

67

0,02439

1,63415

0,00059

66,2256

0,7744

1,1559

0,5998

8

39

62

0,02564

1,58974

0,00066

64,4972

-2,4972

4,0278

6,2362

9

28

47

0,03571

1,67857

0,00128

50,578

-3,578

7,6128

12,8021

10

44

67

0,02273

1,52273

0,00052

68,5235

-1,5235

2,2738

2,3209

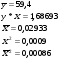
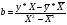
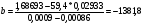
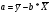
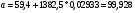
Уравнение гиперболической модели:

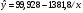
Рассчитаем коэффициент детерминации по формуле (1).

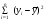=930,4;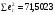

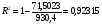
Вычислим среднюю ошибку аппроксимации А по формуле (2):

А=0,1*38,1488=3,81488%

Коэффициент эластичности рассчитаем по формуле (3):

%

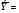
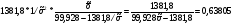Построим график функции с помощью MS Excel.

Рис. 5 График гиперболического уравнения регрессии.

9. Для указанных моделей найти коэффициенты детерминации, коэффициенты эластичности и средние относительные ошибки аппроксимации. Сравнить модели по этим характеристикам и сделать выводы.

Коэффициенты были рассчитаны в задании 8. Для сравнения моделей составим сводную таблицу 11:

Таблица11. Сводная таблица характеристик моделей.

параметры

модель

Коэффициент детерминации, R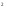

Коэффициент эластичности,(%)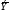

Средняя относительная ошибка аппроксимации, А (%)

Линейная

0,917

0,788

3,648

Степенная

0,909

0,692

4,22

Показательная

0,896

0,817

4,317

Гиперболическая

0,923

0,638

3,815

Для всех моделей средняя относительная ошибка аппроксимации не превышает 7%, значит, качество всех моделей хорошее. Коэффициент детерминации более приближен к 1 у гиперболической модели, таким образом, эту модель можно взять в качестве лучшей для построения прогноза. Для гиперболической модели степень связи между факторным и результативным признаком самая низкая, т.к. 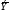имеет наименьшее значение, а для показательной модели самая высокая, т.к. коэффициент эластичности наибольший.