ТЕХНОЛОГИЧЕСКАЯ КАРТА УРОКА

предмет

МАТЕМАТИКА( алгебра и начала анализа)

класс

10

ТЕМА

Формулы суммы (разности) синусов и косинусов двух аргументов

Тип урока

Урок постановки учебной задачи, отработка умений и рефлексии

Технология

сотрудничества

Этапы урока

Задачи этапа

Деятельность учителя

Деятельность ученика

УУД

Организационный момент

Самоопределение к деятельности.

Создание благоприятного психологического климата. Положительный настрой на работу,

Приветствие, мотивация к учебной деятельности

На столе у каждого учащегося есть памятка по тригонометрии, бланк, в котором вы сами будете отмечать степень своего участия в работе на уроке на каждом этапе урока.

Самоопределение к учебной цели

Личностные:

Самоопределение

Регулятивные:

Целеполагание

Коммуникативные:

Планирование учебного сотрудничества с учителем и сверстниками

Этап актуализации опорных знаний и фиксирование индивидуального затруднения

создание условий для осознанного восприятия нового материала.

Актуализация опорных знаний и способов действий

1. Когда мы начинаем изучать новую тему по математике, всегда задаем себе вопрос: «А для чего нам нужно изучать эту тему? Пригодится ли она мне где-нибудь в жизни?

Вам было предложено домашнее задание найти ответ на вопрос : «Где же применяется тригонометрия, в каких профессиях она важна? Что означает слово тригонометрия?»

Показать несколько слайдов на применение тригонометрии.

На слайде высказывание «Если вы хотите участвовать в большой жизни, то наполняйте свою голову математикой, пока есть к тому возможность. Она окажет вам потом огромную помощь во всей вашей работе. (М.И. Калинин)»

2. Математический диктант

Через проектор показываются задания двух вариантов

Выполнение диктанта (2 вар-та, 5 мин)

3) На слайде решение заданий диктанта (3 мин)

4) На слайде критерии оценивания диктанта.

5) Выставите, пожалуйста оценки в таблицу за данный этап урока.

Поднимите, пожалуйста руки, у кого нет ни одной ошибки?

Отвечают на поставленные вопросы.

Выполняют задание (на 2 варианта)

самопроверка

Вариант1

1. Запишите формулу синуса двойного угла

2. Запишите формулу для нахождения Sinα, если известен Cosα

3. Вычислите значение выражения

Sin15⁰ (cos²7⁰30^’-sin²7⁰30^’)

4. Допишите формулу Sin(α –β)=

5. Запишите алгоритм решения данного уравнения Sin2x –Cos2x=1

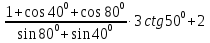
Вариант2

1. Запишите формулу косинуса двойного угла

2. Запишите формулу для нахождения tgα, если известныCosα и Sinα

3. Вычислите значение выражения

2(sin²37⁰30^’-cos² 37⁰30’) sin75⁰

4. Допишите формулу Cos(α –β)=

5. Запишите алгоритм решения данного уравнения Sin²2x+2Sin2x-3=0

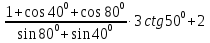
Взаимопроверка диктанта. Учащиеся обмениваются своими листами с диктантом. Оценивают работу одноклассника, выставляют оценки в таблицы результатов за данный этап урока

Коммуникативные:

Сотрудничество с учителем и сверстниками

Познавательные:

Логические-анализ объектов с целью выделения признаков

Уметь использовать формулы суммы и разности одноименных функций при решении уравнений, упрощении выражений.

Личностные:

Навыки самопроверки и самооценки

Этап выявления места и причины затруднения

Постановка учебной задачи

Мотивация изучения

Постановка проблемной задачи:в чем именно состоит недостаточность их знаний, умений или способностей.

Давайте составим алгоритм решения тригонометрических уравнений.

Назовите формулу понижения степени дляcos² x

Назовите формулу понижения для sin² x

Назовите формулу для тангенса двойного угла.

Назовите формулу для косинуса двойного угла.

Используя составленный алгоритм решения уравнений, решите уравнения.

Проверка решенных уравнений ( на слайде решение)

Какую формулу применили для приведения уравнения к простейшему тригонометрическому уравнению?

Возможность применения формул двойного аргумента при решении тригонометрических уравнений:

cos² x – sin² x =1

решить уравнение:

sin5x + sinx=0

какой метод напрашивается?

Назовите методы решения тригонометрических уравнений, приводящие уравнение к простейшему тригонометрическому уравнению?

Хотя бы один из методов позволяет нам решить это уравнение?

Хватает ли нам знания тех формул, которые мы знаем и алгоритма решения тригонометрических уравнений для решения данного уравнения?

Докажем , что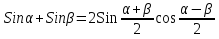

Доказательство на слайде:

Пусть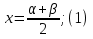

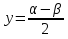(2)

Сложим (1) и (2) выражения,

Получим: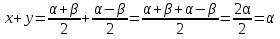

Вычтем (1) –(2)

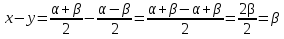Подставим значения 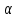и 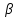в исходную формулу

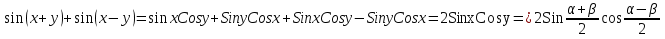
Выявление проблемы

Работа в группах:

Решите уравнение:

1 группа

Cos²2x–Sin²2x=1

2 группа

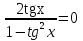
Проверим решение ваших уравнений.

предлагают способы решения, выявляют

Оцените степень своего участия в групповой работе. Выставите себе оценки за данный этап урока в таблицу.

Решите уравнение Sin5x+Sinx=0

проблему: необходима соответствующая формула

формулировка и запись темы урока, постановка дальнейших задач.

Цель урока:знакомство с формулами, позволяющими решать тригонометрические уравнения, содержащие сумму и разность одноименных функций

Записывают формулы и проговаривают их вслух.

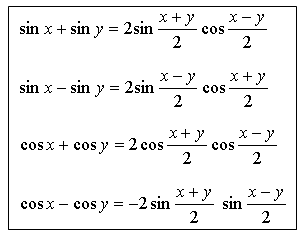
Доказательство одной из формул

Регулятивные:

Умение формулировать проблему

Коммуникативные:

предлагать пути её решения

Познавательные:

Самостоятельное формулирование познавательной цели,ориентировка на разнообразные способы решения

уравнений

Структурирование знаний

Осмысление, систематизация полученных знаний

Изучение и первичное осознание нового учебного материала, осмысление связей между тригонометрическими функциями

ПРИМЕРЫ: записаны на слайде

1. sin6x +sin4x

2. sin43⁰+sin17⁰

3. 

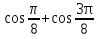
Работа в парах с проговариванием формул

Самопроверка по записи на слайде

Коммуникативные:

Умение работать в парах.

Логические:

Повышение грамотности устной и письменной речи

Познавательные:самостоятельное

создание способов решения,

Первичное закрепление

знаний

Отработка умений применения формул при решении уравнений,установление осознанности изучения темы,

Коррекция выявленных пробелов

Решение предложенного уравнения.

Задания для групповой работы:

Задания 1 группы: на прямое усвоение формул( ср-ср) 9.35 в, стр267

Выполнение заданий в тетради. Ученик решает на доске это уравнение

Регулятивные:

Контроль,коррекция

Познавательные:

Рефлексия выбора формул, условий действий.

Умение принимать решение при выборе задания, развитие самостоятельности

Коммуникативные:

Сотрудничество с партнером,коррекция,оценка действий партнера

Постановка домашнего задания

Обеспечение понимания цели,содержания и способов выполнения домашнего задания:

Выучить формулы суммы и разности синусов и косинусов.

Домашняя самостоятельная работа

(дифференцированная)

Для сильных, средних, слабых уч-ся

Вариант 1

1. Найдите sincostg,

еслиCos2α=0,2 и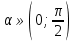

2. Выполните задание из учебника № 9.35 д,ж, стр 267

3. Докажите справедливость формулы разности синусов

Вариант2

1. Найдите

sincostg, если Cos2α=0,6и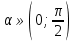

2. Выполните задание из учебника № 9.39 а,гстр 268

3. Докажите справедливость формулы суммы косинусов

Вариант3

1. Найдите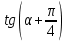

если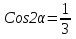 и

2. Выполните задание из учебника № 9.37 а,б стр 268

3. Докажите справедливость формулы суммы косинусов

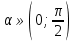
Записывают домашнее задание.

Домашнее задание отправлено учащимся на их электронную почту в прикрепленном к письму файле.

Каждый учащийся самостоятельно определяет, какой вариант он сможет выполнить.

На слайде высвечиваются самостоятельные работы.

Выяснение непонятных моментов.

Определение границ собственных знаний

Уметь работать с тренажерами

Итог урока, рефлексия

Дать качественную оценку работы класса и отдельных учащихся

Воспроизводится слайд с формулами, которые проговариваются.

Оценивание: Каждый учащийся заполняет таблицу

Самоанализ учащимися своих результатов, своей деятельности.

Общий вывод о работе в парах

Представьте в виде произведения

Регулятивные:

Оценка-осознание уровня и качества усвоения темы,

Познавательные: рефлексия

составитель

Васильева Н.М.

ресурсы

С.М.Никольский. «Алгебра и начала математического анализа»,10 кл

М-10

Домашняя самостоятельная работа

«Сумма и разность синусов и косинусов»

Вариант 1

1. Найдите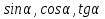еслиCos2α=0,2и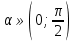

2. Выполните задание из учебника № 9.35 д,ж, стр 267

3. Докажите справедливость формулы разности синусов.

Вариант2

1. Найдите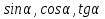, если Cos2α=0,6 и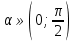

2. Выполните задание из учебника № 9.39 а,г стр 268

3. Докажите справедливость формулы суммы косинусов.

Вариант3

1. Найдите 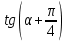, есл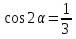и и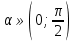

2. Выполните задание из учебника № 9.37 а,б стр 268

3. Докажите справедливость формулы суммы косинусов