Конспект урока по Математике "Производная. Геометрический и механический смысл производной"





 Тема
Тема
Производная. Геометрический и механический смысл производной.
Цель
Повторить, обобщить и систематизировать материал по данным темам. Показать связь понятия производная с геометрией и физикой, показать необходимость знания материала темы при решении прикладных задач. Развивать логическое мышление учащихся, самостоятельность, умение анализировать, навыки самоконтроля. Воспитывать на уроке упорство в достижении конечных результатов, аккуратность, умение применять знания на практике, честность.
Этапы урока
ХОД УРОКА
Создание коллаборатив-ной среды
Организационный момент
Тренинг «Часики», самостоятельное определение темы и цели урока.
Определение темы урока:
Ответьте на мои вопросы:
1) С ее появлением математика перешагнула из алгебры в математический анализ;
2) Ньютон назвал ее «флюксией» и обозначал точкой;
3) Бывает первой, второй,… ;
4) Обозначается штрихом.
Цель нашего урока – повторить основные направления применения производной для решения различных (избранных) задач дифференциального исчисления.
Деление по группам.
Вступительное слово учителя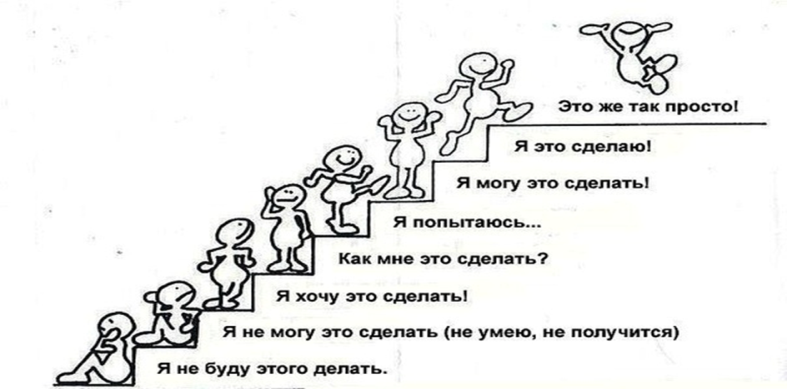
Лестница успеха.
Определите, на какой ступени лестницы в постижении знаний по данной теме находитесь вы сейчас.
Актуализация знаний по теме
Производная относится к числу математических понятий, которые носят межпредметный характер, и широко применяются в физике, химии, биологии, в технике и других отраслях наук. Это в значительной степени повышает роль межпредметных задач при изучении темы: “Производная”. Изучение материала по теме урока имеет принципиально важное значение, так как здесь показывается приложение производной к решению различных физических и технических задач, то есть возможности применения элементов дифференциального исчисления в описании и изучении процессов и явлений реального мира. Производная – одно из фундаментальных понятий математики. Оно возникло в XV11 веке в связи с необходимостью решения ряда задач из физики, механики и математики, но в первую очередь следующих двух: определение скорости прямолинейного движения и построения касательной к прямой. Независимо друг от друга И.Ньютон и Г.Лейбниц разработали аппарат, которым мы и пользуемся в настоящее время.
В настоящее время понятия производной находит большое применение в различных областях науки и техники.
Давайте вспомним основные направления применения производной.
производная
Повторение таблицы производных, графиков функций и их производных.
Работа в группах
(2 группы)
Деление на 3 группы
Решение
задач
(геометрический смысл производной)
Механический смысл производной
Тестирование
Работа с таблицей производных. (горячий стул внутри группы, взаимооценивание)
Устно найти производные функций. (фронтально)
«Собери четверку», работа с графиками.
(индивидуальная работа с взаимопроверкой)
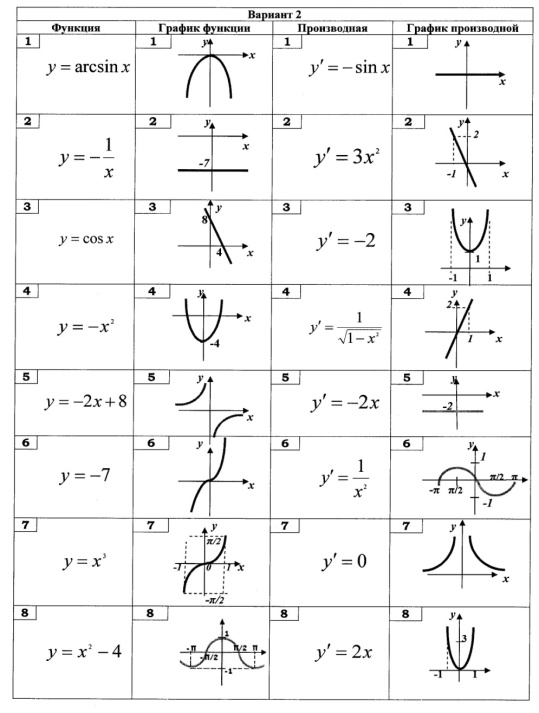
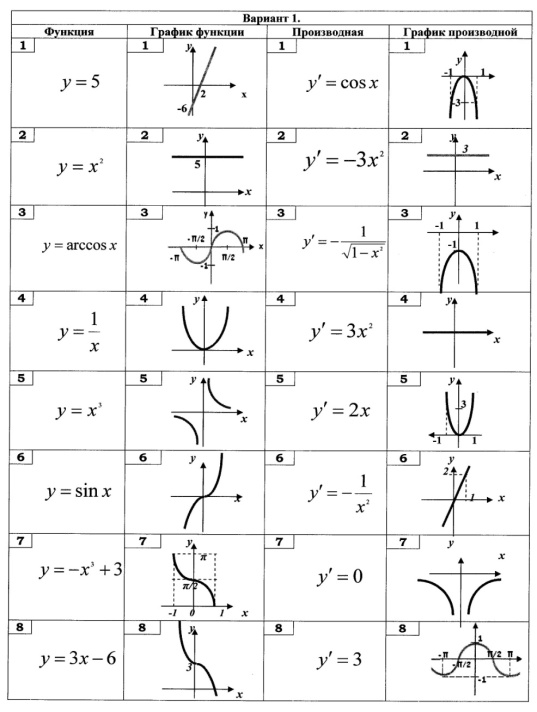
1)Геометрический смысл производной
2)Механический смысл производной
Геометрический смысл производной состоит в том, что значение производно в точке равно угловому коэффициенту касательной к графику функции в этой точке.
Касательная к графику дифференцируемой в точке х0 функции f- это прямая, проходящая через точку (х0; f (х0)) и имеющая угловой коэффициент f’(х0).
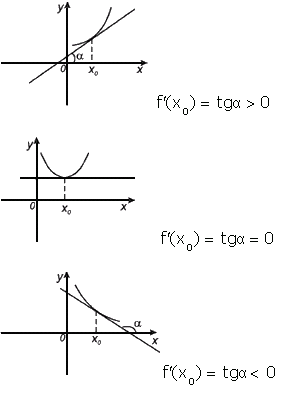
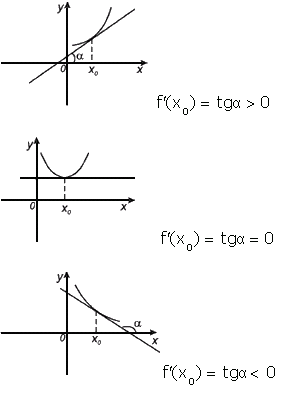
Механический смысл производной
Если на дороге произошла авария, то инспектора полиции интересует скорость в момент аварии. Как она называется?
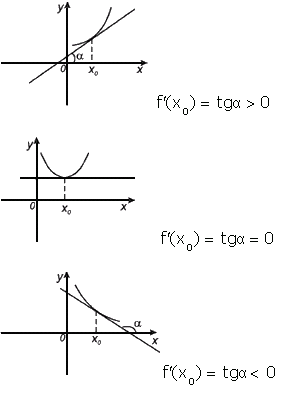
Как связана мгновенная скорость с производной?
Если точка движется вдоль оси х и ее координата изменяется по закону х(t), то мгновенная скорость точки V(t) = x’(t).
Механический смысл производной состоит в том, что производная от координаты по времени есть скорость (V(t) = x’(t) ). Производная от скорости по времени есть ускорение. (a = v’(t) )
Тангенс угла наклона касательной есть величина, показывающая мгновенную скорость изменения функции в данной точке, т.е. новая характеристика изучаемого процесса. Эту величину Лейбниц назвал производной; Ньютон говорил, что производной называется сама мгновенная скорость.
Можно ли по графику определить чему равно значение производной в точке х0, т.е. в точке касания?
(работа по графикам)
Дана функция у(x) = x² – 2х. Напишите уравнение касательной к графику этой функции в точке с абсциссой х0 = 2.
Дана функция у(x) =
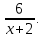 Напишите уравнение касательной к графику этой функции в точке с абсциссой х0 = - 4.
Напишите уравнение касательной к графику этой функции в точке с абсциссой х0 = - 4. Дана функция у(x) = sin 2x . Напишите уравнения касательных к графику этой функции в точках с абсциссами х0 = 0 и х0=
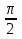 .
.
Ответы
а) у = 2х – 4,
б) у = - 1,5х - 9 ,
в) у = 2х и у = -2х + π .
1.Лифт после включения движется по закону s(t) = t² + 2t + 12. Найти скорость лифта в конце 5 секунды.(12 м/с)
2.Лыжник , спускаясь с горы, движется по закону s(t) = 0,5t² - t. Найти скорость и ускорение лыжника в момент времени t= 3 с, если расстояние измеряется в метрах. Какое это движение?
(v(3) = 2 м/с; а = 1 м/с; равноускоренное движение)
3. Тело массой 10 кг движется прямолинейно по закону: S (t) = 3t2 + t + 1 . Найдите кинетическую энергию тела через 4 с после начала движения.
(Решение: Ek = (mv2)/2, Найдем скорость движения тела в момент времени t: v = S’(t) = (3t2 +t + 1)’ = 6t + 1. Вычислим скорость тела в момент времени t = 4c; v(4) = 6 ∙ 4 + 1 = 25. Ek = (10∙ 252)/2 = 5 ∙ 252 = 3125 (Дж)
« Производная. Геометрический и механический смысл производной»
1 Вариант
1. Точка движется прямолинейно по закону S(t)=2t3 +0,5t2-t.
Вычислите скорость при t=1.
1) 5 2) 7 3) 6 4) 9

2. Найдите угловой коэффициент касательной к кривой 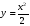 в точке с абсциссой х
в точке с абсциссой х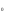 =8
=8
1) 1 2) 32 3) 16 4) 8
3. Под каким углом к оси Ох наклонена касательная проведённая к кривой 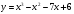 в точке М
в точке М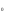 (2;-4) ?
(2;-4) ?
1) 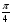 2)
2)  3)
3) 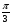 4)
4)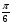

4. Прямая 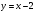 касается графика функции
касается графика функции 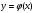 в точке
в точке 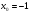 .Найдите
.Найдите 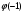 .
.
1) 1 2) -3 3) -2 4) 2
5. Найдите тангенс угла наклона касательной к положительному направлению оси Ох, проведённой к графику функции 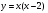 в точке с абсциссой
в точке с абсциссой 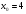 .
.
1) 8 2) 6 3) 4 4) 0
2 Вариант
1. При прямолинейном движении тела путь S(t) (в метрах) изменяется по закону S(t)=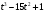 . В какой момент времени ускорение будет равно нулю?
. В какой момент времени ускорение будет равно нулю?
1) 5с 2) 10с 3) 0с 4) 0,2с
2. Под каким углом к положительному направлению оси абсцисс наклонена касательная, проведённая в любой точке кривой 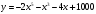 ?
?
1) острым 2) тупым
3) прямым 4) параллельна оси Ох
3. Найдите угловой коэффициент касательной, проведенной к графику функции 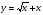 в точке с абсциссой
в точке с абсциссой 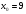
1) 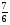 2)
2) 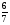 3)
3) 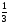 4) 3
4) 3
4. Дана функция 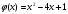 . Найдите координаты точки, в которой угловой коэффициент касательной к графику функции равен 2.
. Найдите координаты точки, в которой угловой коэффициент касательной к графику функции равен 2.
1) (4; 3) 2) (-3; 3) 3) (3; -2) 4) (2; -3)
5. Угловой коэффициент касательной, проведённой к графику функции 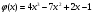 в точке с положительной абсциссой
в точке с положительной абсциссой 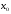 ,равен 2. Найдите
,равен 2. Найдите 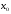 .
.
1) 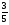 2) 0 3)
2) 0 3) 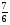 4) 1
4) 1
Рефлексия
Подведение итогов урока
Рефлексия Притча: Шёл мудрец, а навстречу ему 3 человека, которые везли под горячим солнцем тележки с камнями для строительства. Мудрец остановился и задал каждому по вопросу. У первого спросил «Что ты делал целый день? И тот с ухмылкой ответил, что целый день возил камни. У второго мудрец спросил «А что ты делал целый день?» и тот ответил «А я добросовестно выполнял свою работу». А третий улыбнулся, его лицо засветилось радостью и удовольствием «А я принимал участие в строительстве храма»
Ребята, давайте мы попробуем с вами оценить каждый свою работу за урок.
Кто возил камни? (подним. жёлтые жетоны)
Кто добросовестно работал? (подним.синие жетоны)
Кто строил храм? (подним.красные жетоны)
Лестница успеха (добавить, на какой ступени лестницы успеха находитесь вы сейчас и сделать вывод – поднялись ли вы хоть на одну ступень выше?)
Домашнее задание. Выбрать из тестовых заданий ЕНТ задачи на применение геометрического и механического смысла производной

Нравится материал? Поддержи автора!
Ещё документы из категории математика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ