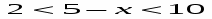
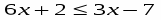
Тема урока: Решение неравенств 1-ой степени с одной переменной.

Цели урока:

- формирование умений и навыков решения неравенств 1-ой степени с одной переменной;

- развитие навыков тождественных преобразований, вычислительных навыков;

- развитие навыков логического мышления, речевой культуры.

Дидактический материал: карточки для парной работы, дифференцированные карточки для самостоятельной работы.

Ход урока:

1.Оргмомент. Открыть тетради, записать число.

Слово учителя ( мотивация ).

Решение неравенств имеет такое же большое практическое значение, как и решение равнений, т.к. многие задачи не только математического содержания сводятся к решению неравенств. В курсе алгебры и начал анализа рассматривается такая важная тема « Исследование функции», в которой с помощью неравенств находятся промежутки возрастания и убывания функции, промежутки знакопостоянства, область определения функции. С помощью неравенств находится область допустимых значений, иррациональных уравнений. Многие задачи прикладного характера связаны с оценкой величин.

Вы уже частично знакомы с понятием линейных неравенств.

2. Актуализация знаний.

Давайте вспомним, что мы уже знаем из данной темы (слайды 2-7 ).

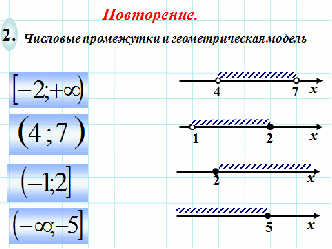
Задание 1. Каждому неравенству соответствует графическая иллюстрация, а каждому изображению дается название (интервал, луч, открытый луч). Каждому неравенству поставьте в соответствии числовой промежуток, геометрическую модель (назовите его).

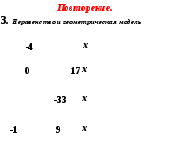
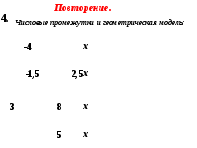
Задание 2. Для каждого промежутка укажите количество целых чисел, входящих в него, наибольшее целое число и наименьшее целое число (если такое есть).

Задание 3. Мы уже встречались с вами с работой, в которой нужно доказать неравенство. Выполните доказательство устно , ссылаясь на свойства числовых неравенств.

А теперь перед нами стоит задача – научиться решать более сложные неравенства, но которые можно свести к линейным.

3. Изучение нового материала.

В 1577 г., когда Роберт Рекорд впервые ввел знак равенства,  он мотивировал свое нововведение следующим образом: никакие два предмета не могут быть между собой более равными, чем два параллельных отрезка. Знак равенства Рекорда стал, однако, общеупотребительным лишь в XVIII веки, после того, как им стали пользоваться Лейбниц и его последователи. Исходя из знака равенства Рекорда, другой английский ученый Гарриот ввел употребляемые поныне знаки неравенства, обосновывая (в “Практике аналитического искусства”, вышедшей в 1631 г. Посмертно) нововведение следующим образом: если две величины не равны, то отрезки, фигурирующие в знаке равенства, уже не параллельны, а пересекаются. Пересечение может иметь место справа ( > ), или слева ( < ). В первом случае образованный знак неравенства будет обозначать “больше”, во втором “меньше”. Несмотря на то, что знаки неравенства были предложены через 74 года после предложенного Рекордом знака равенства, они вошли в употребление намного раньше последнего. Одна из причин этого явления коренится в том, что типографии применяли в то время для знаков неравенства уже имевшуюся у них латинскую букву   V, тогда как наборного знака равенства (=)  у них не было, а изготовлять его тогда было нелегко. (слайд 8)

Итак, каковы же методы решения неравенств. Сегодня мы изучим решение линейных неравенств. (слайд 9)

1. (слайд 10),

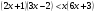2. (решение объясняет учитель, выполняя все 4 этапа решения неравенства).

3. Решение неравенств (особые случаи):

4. Закрепление материала. Задания выполняют учащиеся устно (комментировано) (слайд 11)

При проговаривании ответа указывается правильное название числового промежутка.

4. Работа по закреплению материала ( работа в парах ).

У каждого на столе находятся карточка для парной работы. Сначала один ученик решает и комментирует решение первого неравенства соседу, затем наоборот. Второе неравенство решает каждый самостоятельно. После окончания работы оцените ее , затем оцените работу соседа, обменявшись тетрадями. Свои оценки проставьте в оценочный лист.

Карточка для парной работы.

Вариант 1. Вариант 2.

Решить неравенство: Решить неравенство:

1) 4( 2 – 3х ) – ( 5 – х ) > 11 – х. 1) 2( 2х – 3 ) > 1 – 2( х + 5 ).

2) 3 ( х – 4 ) – 7 ≤ 3 – 2( х + 6 ). 2) 6х ≥ 2( 1 – х ) – 3( х + 1 ).

Ответы: 1) ( - ∞ ; - 0,8 ); Ответы: 1) ( - 0,5; + ∞ );

2) ( - ∞; 2] . 2) [ - 1/11; + ∞ ).

4. Решение упражнений из задачника (повышенной сложности)

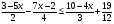(№40.13в)

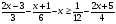(40.16г)

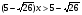(40.11б)

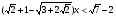(40.11д)

4. (в оставшееся время) Решение двойных неравенств. При решении двойных неравенств нужно помнить, что оно содержит три части («левая», «центр», «правая»). Поэтому, решая, переносит нужно в две части и делить нужно две части. Рассмотрим два наиболее часто встречаемых случая (слайд 12):

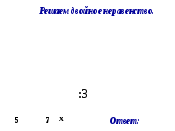
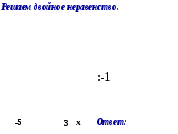
5. Подведение итогов. Слова И.С. Тургенева «Учение — только свет, по народной пословице, — оно также и свобода. Ничто так не освобождает человека, как знание…». Я желаю вам, достигнуть в данной теме таких знаний, чтобы быть свободными. (слайд 13)